Лабораторный практикум Компютерное модел 2007

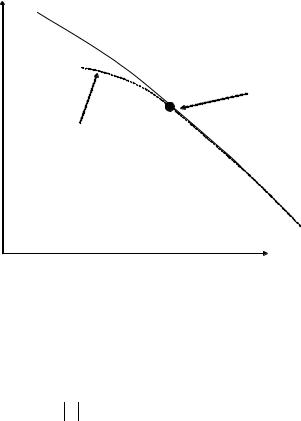
Рассмотрим термодинамический переход из неупорядоченной фазы, существующей при более высокой температуре (нормальное состояние) в состояние с большим порядком и меньшей симметрии. Выше температуры фазового перехода Tc система имеет одно доступное состояние. Ниже Tc система находится в сверхпроводящем состоянии с более низкой свободной энергией (рис. 9.1).

Свободная

энергия

начало фазового перехода

Ветвь с наименьшим значением энергии

Температура

Рис. 9.1. Качественная зависимость свободной энергии для нормальной и сверхпроводящей фаз как функция температуры. Ниже критической температуры Tc система подвергается фазовому переходу второго рода в сверхпроводящее состояние

2. Основная проблема – найти выражение для свободной энергии в сверхпроводящем состоянии. Предполагается, что параметр

порядка имеет вид: ψ = ψ exp(iθ) . Когда параметр порядка ноль,

система находится в нормальном состоянии. Если же параметр порядка отличен от нуля, то система является сверхпроводящей. Вводится основное предположение, что плотность сверхпроводящих частиц (электронов) связана с нормой параметра порядка – ns ~ ψ 2 .

61

Самые существенные независимые переменные – температура и параметр порядка. Поскольку параметр порядка является мал в начале фазового перехода, плотность свободной энергии записывается как ряд по ψ:

f = fn +αψ +βψ2 +cψ3 + dψ4 ,

(9.1)

где f – полная свободная энергия равна свободной энергии нормального состояния fn плюс добавки из-за сверхпроводимости. Таким образом, параметр порядка минимизирует свободную энергию системы. Поскольку параметр порядка ψ является комплексным,

то необходимо учитывать только четные степени порядка |ψ|2 и

|ψ|4.

Таким образом, корректное выражение для свободной энергии:

f = fn +α(T )		ψ		2 +β(T ) / 2		ψ		4 .	(9.2)

Коэффициенты α и β – константы, определенные для данной температуры и также зависящие от состояния системы. Минимум свободный энергии для параметра порядка отличного от нуля может существовать только, если α < 0 и β > 0. В этом случае, свободная энергия как функция параметра порядка находится, как показано на рис.9.2, и в состоянии равновесия ψ0 = −α / β . Параметры α и β

зависят от температуры, и они определяют значение параметра порядка так, чтобы он изменился между ψ = 0 и ψ0. Уравнение (9.2) и есть уравнение Гинзбурга – Ландау, содержащее основную физику фазового перехода системы.

3. Описание системы с любым пространственным изменением требует модификации вида свободной энергии с целью учета градиента параметра порядка:

f = fn +α(T )

ψ

2 +β(T ) / 2

ψ

4 +

1

h ψ

2 .

(9.3)

2m

r

Наконец, если образец находится во внешнем магнитном поле

H

, необходимо включить векторный потенциал A , магнитную

индукцию Br = × A , что дает обобщение выражения для плотно-

сти свободной энергии:

r

2

r

2

f = fn +α(T )

ψ

2 +β(T ) / 2

ψ

4 +

H

+

1

(−ih − eA)ψ

.

8π

2m

c

62

(9.4)

Первое из добавленных слагаемых – энергия магнитного поля, второе представляет кинетическую энергию заряженных сверхпроводящих носителей.

Временная зависимость уравнений Гинзбурга – Ландау

Поскольку система рассматривается при постоянной температуре, перейдем к плотности свободной энергии Гиббса. Свободная энергия Гиббса G преимущественно используется для химических систем и включает работу, требуемую для удаления магнитного

поля из образца.	Учитывая, что эта энергия имеет вид
U =1/ 8π ∫Br HrdV ,	получаемg = f −1/ 4π B Hr . Интегрируя по

всему объему, получаем полную энергию Гиббса:

r

2

fn

+ α

ψ

2 + β / 2

ψ

4 +

H

+

8π

G = ∫dV

1

r

2

r

r .

(9.5)

eA

B

H

+

(−ih −

)ψ

−

2m

c

4π

Этот функционал энергии в стационарном состоянии должен быть минимизирован по основным переменным (ψ, A). Условия минимизации могут быть написаны как функциональные производные:

δG	= 0,	δG	= 0 .	(9.6)
δψ		δA
		r

Уравнения (9.6) определяет независимые от времени уравнения Гинзбурга – Ландау, если G – свободная энергия Гиббса. Если же описывается неравновесная система, то для описания используются условия релаксации той же самой свободной энергии G:

∂ ψ	= − Γ	δ G	,	∂A	= − Γ	δG	= 0 ,	(9.7)
∂ t				∂ t		δ Ar
		δ ψ −

где скорость релаксации системы контролируется коэффициентом Г, называемым коэффициентом Онзагера. Эта модель известна как модель Глаубера.

63

Движущие силы модели Глаубера имеют чисто релаксационную природу и предполагают, что система будет всегда переходить в состояние с более низкой свободной энергией без любых самопроизвольных переходов. В рамках современных полевых теорий учи-

тывается слагаемое F% , описывающее ланжевеновский шум. Такой источник шума необходим, чтобы в явном виде включить теплорегулируемые переходы в теорию. Без этого система всегда оставалась бы в метастабильном состоянии.

Если вычислить две функциональные производные (приложение к методическим указаниям), то получим:

r

1

∂ψ

+ α ψ +β

ψ

2 ψ +

1

(−ih −

eA

)2 ψ + F%

= 0;

(9.8)

Γ

∂rt

2m

c

1

∂A

1

r

r

e

e

r

*

+

×( ×

A − H )−

ψ(−ih −

A)

ψ

Γ

∂t

4π

2mc

c

e

e

r

.

+

ψ* (ih +

A)ψ = 0.

2mc

c

Второе уравнение может быть записано как

r

r

r

2

r

1

∂A

1

×( × A − H )−

ihe

(ψ ψ* −ψ* ψ) +

e

2

A = 0.

+

ψ

2

Γ

∂t

4π

2mc

mc

(9.9)

Первое уравнение описывает релаксацию параметра порядка. Легко видеть, что стационарное, постоянное по образцу решение ψ имеет вид ψ0 = −α/ β .

Во втором уравнении, второе слагаемое представляет ток, инициализирующийr локальное магнитное поле. Для стационарной сис-

темы имеем ∂A / ∂t = 0 и мы видим, что последние два слагаемых должны составлять сверхпроводящий ток. Например, одно из граничных условий для этой системы то, что ток из образца равен нулю, или

		e	r			r		r
	(ih +		A) ψ		= 0,	× A		= H.
		c		bond			bond

64

Учет возможного токового состояния

Модель, в которой полный ток разделяется на нормальный и сверхпроводящий ток, называют моделью двух жидкостей. Это подразумевает разделение концентрации электронов на концентрации нормальных и сверхпроводящих носителей. Фактически, параметр порядка представляет собой долю сверхпроводящих электронов, "объединенных" в куперовские пары.

Для системы, не находящейся в равновесии, первый член второго уравнения (9.8) должен быть связан с полным током, но (на данном уровне описания) это уравнение описывается только сверхток

в образце. Фактически слагаемое Γ−1 ∂A / ∂t пропорционально кинетической индуктивности сверхпроводящих электронов. Обобщая на случай с нормальным током, мы должны добавить влияние электрического поля.

Мы знаем, что полный ток связан с магнитным полем выраже-

нием	4π r				r r
r			=	4π		(9.10)
×H =	c	J		c	(Jn + Js ) .

Сравнивая уравнение (9.10) с уравнением (9.9), мы видим, что сверхпроводящий ток

Jrs		ihe	(ψ ψ* −ψ* ψ) −	e	2			2	r
	=						ψ		A .	(9.11)
		2m		mc

Поскольку ток сверхпроводящих электронов не рассеивает энергию, то только ток нормальных электронов отвечает за электриче-

ское поле. В модели двух жидкостей, слагаемое Γ−1 ∂A / ∂t , отвечающее за релаксацию А, должно ассоциировать и с нормальным током, т.е. необходимо заменить кинетическую индуктивность на проводимость используя стандартные соотношение:

	r	r	1		∂A
					r
	Jn = σ E ,	E +	c			= − ϕ.	(9.12)
					r∂t
		r
	Собирая выражения в форме	Jt = Jn	+ Js , получим вместо систе-

мы (9.8) уравнения вида:

65

1

∂ψ

+α ψ+β

ψ

2 ψ+

1

(−ih −

eA

)2 ψ+ F% = 0;

Γ

∂t

r

2m

c

c

r

σ

ihe

∂A

−σ ϕ+

(ψ ψ* −ψ* ψ) −

× × A = −

4π

c

∂t

2m

−e2 ψ 2 Ar+ c ×Hr. mc 4π

(9.13)

Второе уравнение теперь учитывает полный ток (нормальный и сверхпроводящий). Отметим, что коэффициенты, определяющие

скорость релаксации основных переменных ψ и A , оказываются теперь разными.

Градиентные преобразования уравнений Гинзбурга – Ландау. Безразмерный вид уравнений. Элементы алгоритма

Уравнение (9.13) должно быть неизменно при градиентных преобразованиях типа:

	ie	χ		r r	1 ∂χ
ψ → ψ′ ehc			,	A → A′+ χ,	ϕ → ϕ′− c ∂t	, (9.14)

где χ – произвольная функция. Чтобы оба уравнения (9.13) были инвариантны, добавим к первому уравнению (9.13) слагаемое, пропорциональное произведению ϕ ψ :

r

1

∂ψ

+

ie

ϕ ψ + α ψ +β

ψ

2 ψ +

1

(−ih −

eA

)2 ψ + F% = 0.

Γ

∂t hΓ

2m

c

(9.15)

Полученные уравнения (9.13) и (9.15), оказываются достаточно правильным относительно уравнений Максвелла, соответствуют зависимым от времени уравнениям Гинзбурга–Ландау, в том числе (с учетом 9.15) подобны виду уравнений, полученных из микроскопики Горьковым и Элиашбергом [51].

66

В этой версии уравнений TDGL также выполняется баланс между энергией системы и диссипацией тока. Действительно, предельный переход к случаю однородного полупространства и постоянного r магнитногоr поля дает уравнение Лондонов× × A + λ−2 A = 0 , с характерной глубиной проникновения магнитного поля:

λ =

mc2

=

mc2β

, ψ

0

2

=

α

.

(9.16)

4πe2

ψ0

2

4πe2

α

β

Другой предельный переход – отсутствие магнитного поля – в стационарном случае приводит к уравнению:

		2		h2	2
α ψ +β	ψ		ψ +			ψ = 0 ,	(9.17)
				2m

которое дает решение для параметра порядка вблизи границы

ψ = ψ0 tanh[(x − x0 ) / 2 ξ],	ξ =	h2					,	(9.18)
		2m		α

где ξ – характерная длина когерентности.

Далее, предполагается, что температурная зависимость длины когерентности и глубины проникновения магнитного поля имеют вид

ξ(T ) =		ξ(0)	, λ(T ) =	λ(0)	,
	(1	1/ 2		1/ 2
		−T )		(1−T )

где T – температура в единицах Tс.

Используя эти две характерные величины, введем безразмерные переменные (табл. 9.1).

67

Таблица 9.1

mc2β

h2

Hcm =

4πα2

1/ 2

λ =

ξ =

(

β

)

4πe2

α

2m

α

κ =

λ

=

β

mc

ψ02 =

α

,

ψ = ψ0 Λ

x = ξ x'

ξ

2π

eh

β

H =

2Hcm H '

j =

cHcm

j

'

A = H

c2

(0) ξ A'

2

2πξ

= 2Hcm λ

2

2

πh

g =

α

g'

G = αβ ξ3 G'

t =

t'

(96k T )

β

b c

Здесь,

kB –

постоянная Больцмана, Hc2 (0)

– верхнее критиче-

ское магнитное поле для сверхпроводников 2-го рода при нулевой температуре.

Используя эти переменные, а также соотношение

• 4πλ2 (T )σ

ξ2

(T )Γ

πh

T −1

T −1

,

=

=

1

−

≡ t0 1

−

c

2

12

96k

T

T

T

B

c

c

c

вводим преобразование скалярного и векторного потенциалов, а также параметра порядка и получаем безразмерный вид уравнений

TDGL:

r

2

∂

1

r

Λ+(1−T )(

2

−1)Λ

%

r

(

+iΦ)Λ = −

(r

,t);

∂t

η

i

− A

Λ

+ f

2 r r

r

*

r

r

r

(

∂A

−Φ]

+

(9.19)

κ × × A = (1−T ) Re Λ

i

− A)Λ +[−

∂t

j

j

super

norm

+[κ2 × Hr]

,

r

j

exter

68

→

A; Re – реальная

скалярный потенциал; f% – тепловые флуктуации; κ – параметр ГЛ; константа η – положительная величина, определяющая отно-

где введены безразмерные величины: Λ – параметр	порядка
r	Φ(rr) –
[0 ÷ 1]; A – векторный потенциал; Т – температура [0 ÷ 1];

шение характерных времен релаксации для ∆ и часть комплексной величины.

Последнее слагаемое уравнений (9.19) представляет внешний ток rjexter с условием rjexter = 0 . На данном этапе реализованного алгоритма он будет опущен.

В безразмерных единицах, динамика сверхпроводника зависит только от безразмерного параметра Гинзбурга – Ландау κ . Для

сверхпроводника с κ <1/	2 характерно поведение как сверхпро-
водника I типа, для κ > 1/	2 – как сверхпроводника II типа.
Система уравнений для	∆ и A при определенных начальных

условиях должна быть решена в ограниченной области Ω со следующими граничными условиями:

Граничное условие для A : внешнее магнитное поле He, приложеное в направлении оси z, может быть переменным во времени, но пространственно однородно. Непрерывность поля, таким образом,

подразумевает:	r
	BZ = eˆZ × A .	(9.20)

Граничное условие для параметра порядка ∆: Проекции плот-

ность сверхпроводящего тока, перпендикулярная к границе образ-

ца, равна нулю, а именно:
νˆ (−i − Ar)∆ = 0 ,	(9.21)

где νˆ обозначает единичный вектор, нормальный к поверхности сверхпроводника, граничащей с вакуумом. Это автоматически подразумевает, что нормальная составляющая исчезает, так как полный ток через поверхность сверхпроводник-вакуум равен нулю. Чтобы явно показать это, напомним, что плотность сверхпроводящего и нормального компонента тока равны:

69

J S = (1 − T ) R e[∆* (−i − A)∆],

J N

→

(9.22)

= − ∂ A .

→

→

→

∂t

→

→

→

Перепишем второе уравнение (9.19) как

JN + JS

=κ2× × A .

Проектирование

этого

уравнения

на

нормаль

к поверхности

νˆ = (νx ,νy ,0) приведет к уравнению:

−ν ∂ )B

νˆ J

+νˆ J

=κ2

(ν ∂

→

→

N

S

x

y

z .

(9.23)

∂y

∂x

Так как в (9.23) справа представлена только тангенциальная производная, то правая сторона тождественно равна нулю, т.е. полный ток через границу равен нулю. Намагниченность образца в этом случае можно ввести следующим образом:

MZ (t) =	∫	(BZ (x, y,t) − He )dxdy	.	(9.24)
		4π ∫dxdy

Разностные приближения к уравнениям TDGL обычно получают, используя метод конечных элементов. Наиболее физическим методом расчета TDGL является ψU -метод, в рамках которого

наряду с параметром порядка ψ используются два вспомогатель-

ных поля U x и U y , которые связаны с векторным потенциалом A соотношениями:

			x
	−i		∫						(9.25)
U x (x, y,t) = exp					A (ξ, y,t)dξ ,
						x
			x0
					y
		−i		∫					(9.26)
U y (x, y,t) = exp						A (x,η,t)dη .
							y
				y0

Точка (x0,y0) выбирается произвольно. Эти переменные были применены к уравнениям TDGL в работе [3]. ψU -метод оказался

весьма полезным при численном моделировании многих явлений сверхпроводимости [3, 6 – 8].

70