Мишулина Основы теории вероятностей 2011

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»

О.А. Мишулина

ОСНОВЫ

ТЕОРИИ ВЕРОЯТНОСТЕЙ

Рекомендовано УМО «Ядерные физика и технологии» в качестве учебного пособия

для студентов высших учебных заведений

Москва 2011

УДК 519.21(075) ББК 22.171я7 М71

Мишулина О.А. Основы теории вероятностей: учебное по-

собие. М.: НИЯУ МИФИ, 2011. – 196 с.

Изложены базовые понятия теории случайных событий и случайных величин. Приведены типовые законы распределения вероятностей, применяемые в статистическом анализе данных. Теоретический материал сопровождается многочисленными примерами, которые иллюстрируют основные приемы решения задач по теории вероятностей. По каждой теме курса предложены вопросы и задачи для самоконтроля.

Предназначено для студентов, специализирующихся по прикладной математике и информатике. Книга будет полезна для аспирантов и инженеров как справочное пособие при решении задач прикладного статистического анализа и выполнении статистических вычислений.

ПодготовленоврамкахПрограммысозданияиразвитияНИЯУМИФИ.

Рецензенты:

д-рфиз.-мат. наук, проф. Е.А. Сатаев(ИАТЭНИЯУМИФИ), д-ртехн. наук, проф. С.Д. Кулик(НИЯУМИФИ)

Подписановпечать15.12.2010. Формат60х84 1/16

Печ. л. 12,25. Уч.-изд. л. 12,5. Тираж320 экз.

Изд. №1/1/37 Заказ№2

Национальныйисследовательскийядерныйуниверситет«МИФИ». 115409, Москва, Каширскоеш., 31

ООО «Полиграфический комплекс «Курчатовский». 144000, Московская область, г. Электросталь, ул. Красная, д. 42

4

ПРЕДИСЛОВИЕ

Курс теории вероятностей является базовым при подготовке специалистов по прикладной математике и информатике. Владение основами теории вероятностей необходимо при изучении ряда прикладных математических дисциплин – математической статистики, теории исследования операций, статистического анализа временных рядов, статистического моделирования систем и пр.

Предлагаемое учебное пособие соответствует программе преподавания теории вероятностей студентам факультета «Кибернетика» НИЯУ МИФИ. Учебное пособие включает четыре главы, посвященные случайным событиям, случайным величинам, случайным векторам и типовым законам распределения вероятностей, распространенным в приложениях. В пособии достаточно подробно излагается теория по всем темам курса с доказательствами и комментариями.

Теоретический материал сопровождается многочисленными примерами, которые позволят студентам не только освоить основные приемы решения задач, но и обратить внимание на некоторые положения теории, особенно часто применяемые на практике. По каждой теме курса студентам предлагаются вопросы и задачи для самоконтроля. Ответы к контрольным задачам можно найти в конце книги.

Для приобретения навыков решения практических задач предлагается использовать книги : «Сборник задач по математике для втузов» под ред. Ефимова А.В. (ч. 3 «Теория вероятностей и математическая статистика») и «Теория вероятностей в задачах и упражнениях» Кочеткова Е.С. и Смерчинской С.О., которые наиболее соответствуют содержанию и стилю настоящего учебного пособия.

5

Глава 1. СЛУЧАЙНЫЕ СОБЫТИЯ

§ 1. Понятие случайного события

Теория вероятностей применяется для исследования тех явлений, которые носят массовый характер. Практика показывает, что при многократном наблюдении случайных явлений обнаруживаются определенные закономерности, своего рода устойчивые характеристики, которые свойственны именно массовым явлениям. Классическим примером эффективного применения статистического подхода является газодинамика. Благодаря молекулярному строению газа его состояние может быть представлено как совокупность состояний всех молекул в заданном объеме. Однако физические свойства газа не определяются простой суммой состояний отдельных молекул. Вследствие массовости явления возникают качественно новые закономерности, которые устанавливаются с помощью статистического подхода. Статистический анализ и статистические модели нашли широкое распространение во всех сферах деятельности человека – науке, технике, экономике, бизнесе, принятии решений в конфликтных ситуациях и пр.

Основными понятиями при использовании статистического подхода являются испытание (опыт, эксперимент) и случайное событие.

Изучая определенное явление, исследователь фиксирует условия для его возникновения, которые для получения достоверной информации должны оставаться неизменными в каждом эксперименте, при каждой регистрации измеряемых данных. Назовем совокупность условий проведения эксперимента комплексом условий G. Каждое осуществление комплекса условий G будем называть реализацией. Например, можно рассмотреть совокупность измерений температуры воздуха, выполненных на определенной метеостанции 1 июня в 12 часов на протяжении всех лет метеорологических наблюдений. Перечисленные условия измерений составляют комплекс условий G, а каждая его реализация предоставляет оче-

6

редное значение температуры воздуха. В приведенном примере метеорологических измерений исследователю могут быть интересны некоторые события. В частности, могут рассматриваться следующие события:

А1 – температура воздуха не выше 15°; А2 – температура воздуха равна 20°;

А3 – температура воздуха находится в пределах от 20° до 25°. Обычно события обозначают прописными латинскими буквами

А, В, С и т.д., помечая их в случае необходимости нижними индексами.

Если при реализации комплекса условий G изучаемое событие происходит неизбежно, то оно называется достоверным и обозначается U. Если же при реализации комплекса условий G событие никогда не происходит, то оно называется невозможным и обозначается V. Принятые обозначения для достоверного и невозможного событий происходят от английских слов universal и void. Далее будут даны соответствующие пояснения.

Детерминированные законы механики, теории электричества и других разделов физики дают многочисленные примеры достоверных и невозможных событий.

Пример 1.1. При нагревании воды до 100° при 760 мм рт. ст. (комплекс условий G) она превращается в пар (событие U).

Пример 1.2. В замкнутом проводнике, движущемся в магнитном поле (комплекс условий G), возникает электрический ток (событие U).

Пример 1.3. При увеличении температуры идеального газа, имеющего постоянные массу и объем (комплекс условий G), его давление падает (невозможное событие V).

Если при реализации комплекса условий G событие A может как произойти, так и не произойти, то оно называется случайным. События А1, А2, А3, приведенные выше в примере метеонаблюдений, являются случайными.

Последовательность испытаний (т.е. многократное воспроизведение комплекса условий G) называется статистическим экспериментом. Результат статистического эксперимента – последова-

7

тельность событий, имевших место в каждом из испытаний. Например, при случайном бросании монеты в пяти испытаниях может быть реализована последовательность BAABA, где А – выпадение герба; В – выпадение решки.

В каждой практической задаче, связанной с реализацией комплекса условий G, можно выделить элементарные события, которые являются неразложимыми и в одном испытании не могут появляться одновременно. Для элементарных событий обычно используется обозначение ω. Совокупность всех элементарных исходов испытания (элементарных событий) образует пространство элементарных событий Ω.

Построение пространства элементарных событий не всегда имеет однозначное и очевидное решение. Выбор множества элементарных событий связан с возможностью описания с их помощью тех событий, которые сформулированы в поставленной задаче. Согласно определению пространства элементарных событий при его построении следует контролировать выполнение следующих требований:

в каждом испытании непременно реализуется одно событие из пространства элементарных событий;

если в испытании реализуется некоторое элементарное событие, то никакое другое элементарное событие не происходит;

произвольное событие, не являющееся элементарным и соот-

ветствующее рассматриваемому в задаче типу, может быть пред-

ставлено как подмножество пространства элементарных событий, т.е. происходит всегда, когда в испытании происходит одно из элементарных событий рассматриваемого подмножества.

Рассмотрим несколько примеров.

Пример 1.4. Пусть испытание состоит в случайном бросании игральной кости. Естественно считать элементарными исходами ωi, i = 1, 2, …, 6, которые означают выпадение граней с номерами 1, 2, …, 6 соответственно. Таким образом, в этом примере пространство элементарных событий Ω = {ωi, i = 1, 2, …, 6} является конечным. Событие А, состоящее в выпадении грани с четным номером, представляется совокупностью элементарных событий

ω2, ω4, ω6 : А = {ω2, ω4, ω6}.

8

Пример 1.5. Теперь рассмотрим более сложное испытание с игральной костью. Допустим, что кость бросается несколько раз до первого выпадения грани с номером 5. Пусть в условиях испытаний интерес представляет только число бросаний кости до первого выпадения грани с номером 5. Тогда пространство элементарных событий образует счетное множество: Ω = {ωi, i = 1, 2, …}, где ωi – событие, состоящее в том, что грань с номером 5 впервые выпала при i-м бросании игральной кости. Рассмотрим событие В, состоящее в выпадении грани с номером 5 не ранее, чем в десятом бросании кости. Это событие представляется следующим множеством элементарных событий: В = {ωi, i = 10, 11, …}.

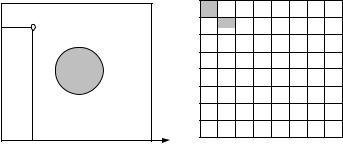
Пример 1.6. Рассмотрим испытание, которое состоит в случайном бросании точки в квадрат на плоскости. В этом случае элементарным событием является попадание точки в фиксированное координатное положение в пределах квадрата, которое представляется парой действительных чисел (x, y) (рис. 1.1, а).

y (x,y)

Рис. 1.1. Иллюстрация к примеру 1.6

Поскольку число действительных чисел на отрезке [0; 1] несчетно, несчетным является и множество элементарных событий. Построенное таким образом пространство элементарных событий позволяет описать, например, событие, состоящее в попадании точки в круг заданного радиуса (не больше половины стороны квадрата) с центром, совпадающим с центром квадрата.

Допустим, что квадрат, как шахматная доска, разделен на 64 перенумерованные клетки (рис. 1.1, б). Кроме того, предположим, что

9

при бросании точки в квадрат интерес представляют не ее точные координаты (x, y), а номер клетки, в которую она попала. В этом случае множество элементарных событий конечно: Ω = {ωi, i = 1, 2, …, 64}, где i – номер клетки. Разнообразие событий, которые можно описать в этом пространстве элементарных событий, много меньше, чем в предыдущем случае. Примером события в такой постановке задачи является принадлежность точки одной из клеток главной диагонали (см. рис. 1.1, б).

Возвратимся к понятиям достоверного и невозможного событий U и V. Из определения достоверного события U следует, что оно имеет место при реализации любого элементарного события, поэтому представляется как полное (universal) множество всех элементарных событий. В то же время невозможное событие V не содержит ни одного элементарного события, так что является пустым множеством (void). Отсюда и следуют принятые для достоверного и невозможного событий обозначения.

Контрольные вопросы и задачи

1.Дайте определения достоверного, невозможного и случайного событий.

2.Приведите примеры достоверного, невозможного и случайного событий.

3.Дайте определение и поясните на примере понятие статистического эксперимента.

4.Какими свойствами обладают элементарные события, образующие пространство элементарных событий?

5.Одновременно бросаются две игральные кости. Рассматриваются различные события, связанные с суммой чисел на выпавших гранях. Опишите пространство элементарных событий.

6.Какие элементарные события, определенные в задаче 5, образуют следующее событие А: сумма чисел на выпавших гранях не более 4?

7.Монета случайно бросается до выпадения решки два раза подряд, но производится не более трех бросаний. Опишите пространство элементарных событий.

10