Орловский Определенный интеграл.Практикум ч.1 2010

2259. Доказать, что одна из первообразных четной функции есть функция нечетная, а всякая первообразная нечетной функции есть функция четная.

1. Пусть функция f четна. Одной из ее первообразных является интеграл с переменным верхним пределом

∫x

F (x) = f(t) dt.

0

Покажем, что эта первообразная нечетна. Делая в интеграле замену u = −t и используя четность f, получаем

∫−x ∫x

F (−x) = f(t) dt = − f(−u) du =

00

∫x ∫x

= − f(u) du = − f(t) dt = −F (x).

0 0

2. Пусть функция f нечетна, тогда любая ее первообразная

имеет вид

∫x

F (x) = f(t) dt + C.

0

Делая в интеграле замену u = −t и используя нечетность f, получаем

−x		x
F (−x) = ∫0	f(t) dt + C = −	∫0	f(−u) du + C =

∫x ∫x

=f(u) du + C = f(t) dt + C = F (x).

0

0

131

2260. Вычислить интеграл

2

1

∫ (1 + x −

)ex+(1/x)dx,

x

1/2

введя новую переменную t = x +

1

.

1

x

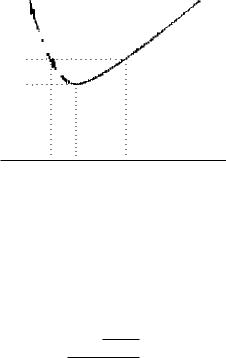
График функции t = x +

приведен на рис. 3.22.

x

t

6

1

q

q

q

t = x +

5/2

x

2

q

q

O

1/q2 1q

2q

-x

Рис. 3.22

На концах отрезка интегрирования значения функции равны 5/2. На промежутке x [1/2; 1] функция убывает, а на отрезке [1; 2] функция возрастает, точка x = 1, t = 2 является точкой минимума. Решая уравнение замены относительно x, приходим к квадратному уравнению x2 − tx + 1 = 0, что дает

√

x = t ± t2 − 4 .

2

Знак минус отвечает левой ветви графика функции (x [1/2; 1]), а знак плюс – правой ветви (x [1; 2]). Для осуществления ука-

132

занной замены интеграл нужно разбить на два:

2	1					1		1
∫ (1 + x −			)ex+(1/x)dx =			∫ (1 + x −			)ex+(1/x)dx+
	x							x
1/2						1/2
		2		(1 + x −		1	)ex+(1/x)dx.
		+ ∫1
						x

В первом интеграле

√√

x =

t − t2 − 4

,

1

=

t + t2 − 4

,

x

2

2

1

(1 −

t

)dt , x −

1

= −√t2 − 4.

dx =

√

2

x

t2 − 4

Таким образом,

4 ) et √t2 − 4 − t dt =

1 + x

1

ex+(1/x)dx = (1

t2

1

2

∫ (

−

)

∫

− −

2√

x

t2

−

4

1/2

5/2

√

5/2

t

√

1)(√

t)

t

2

4

t2

4

= ∫

e

(

− 2−√

−

−

dt.

t2

−

4

2

Во втором интеграле

√√

x =

t + t2 − 4

,

1

=

t − t2 − 4

,

x

2

2

1

(1 +

)dt , x −

1

dx =

√

t

=

√t2 − 4.

2

x

t2 − 4

Следовательно,

4 ) et √t2 − 4 + t dt =

1 + x

1

ex+(1/x)dx =

(1 +

t2

2

5/2

∫(

−

)

∫

√

−

2√

x

t2

−

4

1

2

133

5/2

t

√

√

2

4 + 1)(

t

2

4 + t)

= ∫

e (

t

−

−

2√

dt.

t2

−

4

2

Складывая полученные интегралы, находим:

∫2 (

1 + x −

1/2

∫5/2(

= √ t

t2 − 4

2

5/2

1

)ex+(1/x)dx = ∫

2

+ t

4

t√

−

et dt =

x

t2

4

2

−

√

5/2

(

√

)

2

+ t2 − 4)et dt =

∫

d et

t2 − 4 =

=et √t2 − 4 5/2 = 3 e5/2.

2 2

2261. В интеграле

∫2π

f(x) cos x dx

0

выполнить замену переменной sin x = t.

На всем промежутке интегрирования функция t = sin x не имеет обратной, поэтому рассматриваемый интеграл разбиваем на три:

2π			π/2
∫0	f(x) cos x dx =		∫0	f(x) cos x dx+
	3π/2			∫2π f(x) cos x dx
+	∫	f(x) cos x dx +
π/2				3π/2

и делаем указанную замену в каждом из полученных интегралов.

134

На отрезке [0; π/2] обратной функцией к t = sin x является функция x = arcsin t, при этом cos x dx = dt. Таким образом,

π/2
∫0	f(x) cos x dx =	∫01 f(arcsin t) dt.

На участке [π/2; 3π/2] обратной к t = sin x является функция x = π − arcsin t. Из равенства t = sin x снова получаем cos x dx = = dt, поэтому

3π/2		−1	1
∫	f(x) cos x dx =	∫ f(π − arcsin t) dt = − ∫ f(π − arcsin t) dt =
π/2		1	−1
	= − ∫0 f(π − arcsin t) dt −		∫1 f(π − arcsin t) dt.
	−1		0

На промежутке [3π/2; 2π] функция t = sin x имеет обратную x = 2π + arcsin t. По прежнему cos x dx = dt и

∫2π	f(x) cos x dx = ∫0 f(2π + arcsin t) dt.
3π/2	−1

Складывая полученные интегралы, находим:

∫2π ∫1 ∫0

f(x) cos x dx = f(arcsin t) dt − f(π − arcsin t) dt−

0 0 −1

− ∫1 f(π − arcsin t) dt +	∫0 f(2π + arcsin t) dt =
0	−1

135

∫1

=[f(arcsin t) − f(π − arcsin t)] dt+

0

∫0

+[f(2π + arcsin t) − f(π − arcsin t)] dt.

−1

2262. Вычислить интеграл

∫1 [cos (ln x1 )]′ dx,

e 2n

где n – натуральное число.

После замены t = ln(1/x) получаем, что искомый интеграл

e

1

1

dx

2πn

0

I =

∫2n

sin

(ln

x

)

x

= ∫

| sin t| dt =

= n−1

π+2πk

sin t

dt +

2π+2πk

sin t

dt =

k=0

∫

|

|

∫

|

|

∑

2πk

π+2πk

= n−1

π+2πksin t dt

−

2π+2πksin t dt =

k=0

∫

∫

∑

2πk

π+2πk

=	−	(−cos x		2πk		+ cos x π+2πk			)
	∑			π+2πk			2π+2πk
	n 1
	k=0
2263. Найти				π
						x sin x
				∫				dx.
					1 + cos2 x
				0

n∑−1

=4 = 4n.

k=0

136

Искомый интеграл

π			sin x			π
I = ∫						∫
	x				dx =		xf(sin x)dx,
		2	−	sin2 x
0						0

где

u

f(u) = 2 − u2 .

Согласно решению задачи 2257(б)

π			π
∫0	xf(sin x)dx =	π	∫0	f(sin x)dx.
		2

Применяя эту формулу и делая замену v = cos x, получаем

π

sin x

π

d(cos x)

1

π

π

π

dv

I =

∫

dx =

−

∫

=

∫

=

2

2

−

sin2 x

2

1 + cos2 x

2

1 + v2

0

0

−

1

π

1

π2

=

arctg v −1 =

.

2

4

2264. Найти интеграл

3

1 +′f2

(x) dx,

∫

f (x)

−1

если

(x + 1)2(x − 1)

f(x) =

.

x3(x − 2)

Неопределенный интеграл

∫	1 +′f2(x) dx = ∫	1 + [f(x)]2 = arctg f(x) + C.
	f (x)	d(f(x))

137

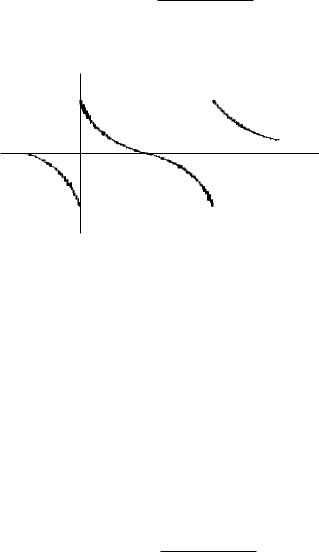
Рассмотрим одну из первообразных подынтегральной функции

F (x) = arctg (x + 1)2(x − 1) . x3(x − 2)

График этой функции представлен на рис. 3.23.

	6y = F (x)		q
q	π2 q	1q		3q
	O		q2		x
−1					-
	−π2 q		q

Рис. 3.23

Функция F (x) имеет две точки разрыва (x = 0 и x = 2) на промежутке интегрирования [−1; 3], поэтому для вычисления определенного интеграла необходимо разбить его на три:

3		1 +′f2(x) dx =			0	1 +′f2(x) dx+
∫					∫
			f (x)				f (x)
−1					−1
+	2				3		1 +′f2(x) dx.
	∫0		1 +′f2(x) dx + ∫2
			f (x)				f (x)

Для вычисления каждого из полученных интегралов можно применить формулу Ньютона – Лейбница:

	0	f′(x)		(x + 1)2(x − 1)		0			π
			dx = arctg				=			,
−
		1 + f2(x)		x3(x 2)			1	− 2
∫
				−
	1				−

138

2	f′(x)		(x + 1)2(x − 1)		2
		dx = arctg				=		π,
0			−
∫	1 + f2(x)		x3(x 2)				−
				0

3	f′(x)				(x + 1)2(x − 1)							3		32		π
			dx = arctg										= arctg				.
∫											2				−
	1 + f2(x)					x3(x	−	2)						27		2
2
Таким образом, окончательно, получаем
		3		f (x)					32
			∫
				′		dx = arctg					− 2π.
				1 + f2(x)					27
		−1

2265. Доказать, что если f(x) – непрерывная периодическая функция, определенная при −∞ < x < +∞ и имеющая период T , то

a∫+T	∫T
f(x) dx =	f(x) dx,	(3.13)
a	0

где a – любое число.

Докажем предварительно, что при любых A и B

B+T	B
∫	∫
f(x) dx =	f(x) dx.	(3.14)
A+T	A

Для этого выполним замену переменной x = y + T в интеграле, находящимся в левой части равенства (3.14). Используя T - периодичность функции f, получим

B+T	B	B	B
∫	f(x) dx = ∫	f(y + T ) dy = ∫	f(y) dy = ∫	f(x) dx.
A+T	A	A	A

139

Для доказательства утверждения задачи воспользуемся свойством аддитивности определенного интеграла:

a∫+T ∫0 ∫T a∫+T

f(x) dx = f(x) dx + f(x) dx + f(x) dx =

a a 0 T

= ∫T f(x) dx +	a∫+Tf(x) dx −	∫a f(x) dx.
0	T	0

Согласно равенству (3.14) с A = 0, B = a

a∫+T ∫a

f(x) dx − f(x) dx = 0,

T0

следовательно,

a∫+T ∫T

f(x) dx = f(x) dx.

a0

2266. Доказать, что при n нечетном функции

∫x ∫x

F (x) = sinn t dt , G(x) = cosn t dt

0 0

периодические с периодом 2π; а при n четном каждая из этих функций есть сумма линейной функции и периодической функции.

Для решения этой задачи потребуется следующее утвержде-

ние

Лемма. Пусть при некоторых T > 0, A R и всех x R

f(x + T ) = f(x) + A.

Тогда

f(x) = φ(x) + AT x ,

140