Орловский Определенный интеграл.Практикум ч.1 2010

следующую:

∫b

f(x) dx = F (b − 0) − F (a + 0).

(3.2)

a

Задача 12. Пусть функция f C[a; b] и F ′(x) = f(x) в интервале (a; b). Доказать, что функция F имеет конечные пределы при x → a и x → b и справедлива формула (3.2).

Формула (3.2) применяется в решениях задач 2213(б), 2216(б, в), 2217, 2264, 2275, 2276. Отметим также задачу 2301, где эта формула распространяется на более общий случай.

Техника вычисления неопределенного интеграла достаточно разработана в курсах математического анализа. Многие формулы этой техники можно перенести непосредственно и на определенный интеграл. К ним, в первую очередь, относятся формулы интегрирования по частям

	b		b			b
a					a
∫				− ∫
	f(x)g′(x) dx = f(x)g(x) a					f′(x)g(x) dx	(3.3)
и формула замены переменной
	∫ab f(φ(x))φ′(x) dx =			φ(b)
				∫	f(t) dt.		(3.4)
			φ(a)

Формула (3.3) применима для любых f, g C1[a; b]. Для применимости формулы (3.4) достаточно, чтобы функция f была непрерывна на области значений функции φ, а функция φ

C1[a; b].

На первый взгляд, формула замены переменной (в применении к определенному интегралу) кажется ущербной, так как по первоначальному определению интеграла нужно предполагать, что a < b и φ(a) < φ(b), что резко сужает класс замен

71

по сравнению с неопределенным интегралом. Простой выход из создавшегося положения дает расширение понятия интеграла: принимается, что для любой функции f

∫a

f(x) dx = 0,

a

а при a > b

∫b ∫a

f(x) dx = − f(x) dx.

ab

При таком расширении понятия интеграла оказывается, что для справедливости формулы (3.4) достаточно, чтобы функция f была непрерывна на области значений функции φ, а φ C1[a; b] либо φ C1[b; a].

Формулу (3.4) часто называют также формулой подстановки. В некоторых учебниках понятия замены и подстановки различают. Переход от интеграла в левой части равенства (3.4) к интегралу в правой части этого равенства назывют заменой φ(x) = t, если же мы делаем переход от интеграла в правой части к интегралу, находящемуся в левой части равенства, то эту процедуру называют подстановкой t = φ(x). Мы не будем делать такого различия.

Формула замены переменной допускает важное обобщение. Эта формула справедлива для любой интегрируемой функции f при условии, что функция g строго монотонна. Доказательство этого утверждения можно найти в классических курсах анализа.

Одну из важных теорем интегрального исчисления представляет теорема о дифференцировании интеграла по переменному верхнему пределу. Если функция f интегрируема на отрезке [a; b], то интегралом с переменным верхним пределом называется

72

функция, заданная формулой
∫x
F (x) = f(ξ) dξ,	(3.5)
x0

где x0 – некоторая точка отрезка [a; b]. Функция F непрерывна на отрезке [a; b], а в точках непрерывности подынтегральной функции f дифференцируема, причем

F ′(x) = f(x).

(3.6)

Эта теорема имеет много применений. Прежде всего отметим, что из нее непосредственно следует, что у любой непрерывной на отрезке [a; b] функции существует (на этом же отрезке) первообразная. Формула Ньютона – Лейбница тоже является непосредственным следствием этой теоремы. С практической точки зрения, мы имеем формулу дифференцирования интеграла

	x
d	∫	f(ξ) dξ = f(x),	(3.7)
dx
	x0

справедливую для любой непрерывной функции f.

Из формулы (3.7), несложно получить несколько более общую формулу

	b(x)
d	∫	f(ξ) dξ = f(b(x))b′(x) − f(a(x))a′(x).	(3.8)
dx

a(x)

Для справедливости этой формулы в некотором интервале x(α; β) достаточно, чтобы функция f была непрерывна на некотором "объемлющем" отрезке [A; B], причем при всех x (α; β) отрезок [a(x); b(x)] [A; B], а функции a(x) и b(x) непрерывно дифференцируемы на (α; β).

Задача 13. Доказать формулу (3.8).

73

Формула (3.8) используется при решении задач 2231 – 2236 и 2256.

Важным свойством определенного интеграла является свойство аддитивности

∫ab f(x) dx = ∫ac f(x) dx + ∫c b f(x) dx.

(3.9)

При расширенном понимании интеграла формула (3.9) оказывается верной для любого взаимного расположения точек a, b и c. Достаточно, чтобы функция f была интегрируема на какомнибудь отрезке, содержащем эти три точки. Формулу (3.9) приходится применять для вычисления интегралов, содержащих модули (задачи 2211, 2218, 2238, 2242). Она необходима и в том случае, когда подынтегральная функция задана разными формулами на разных участках отрезка интегрирования (задача 2237).

Отметим геометрическую интерпретацию определенного интеграла. Если функция f неотрицательна на отрезке [a; b], то интеграл от нее равен площади фигуры, ограниченной прямыми x = a, x = b, y = 0 и графиком функции f. В общем случае интеграл равен разности площадей двух фигур. Одна из них ограничена частью графика функции, лежащей над осью абсцисс, а другая – частью графика, лежащей под осью абсцисс. Этот момент отмечен на рис. 3.1 – 3.13.

Применяя формулу Ньютона – Лейбница, найти определенные интегралы и нарисовать соответствующие криволинейные

площади.

∫8 √

2206. 3 x dx.

−1

	8						8
	1					−
								1	= 4 .
∫ √3 x dx = 4 x4/3
−	3								45

74

6y

q

−

q

1

8q

-x

O

q

Рис. 3.1

Интеграл равен разности площадей фигур, расположенных

над осью абсцисс и под осью абсцисс (рис. 3.1).

∫π

2207. sin x dx.

0

∫π

0

6y

	π
		= 2.
sin x dx = − cos x 0

q

-x

O

π

Рис. 3.2

	√
			3
	∫					dx
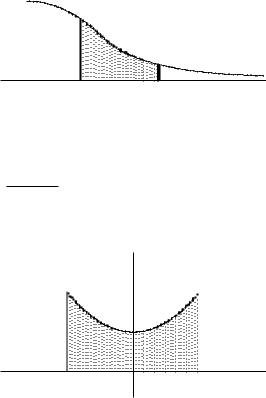
2208.							.
						1 + x2
	1/√
		3

75

√

√

3

dx

3

π

π

π

∫

1 + x2

= arctg x 1/√3

=

3

−

6

=

6

.

1/√

3

6y

q

q

-

O 1/

√q

√q

x

3

3

Рис. 3.3

1/2

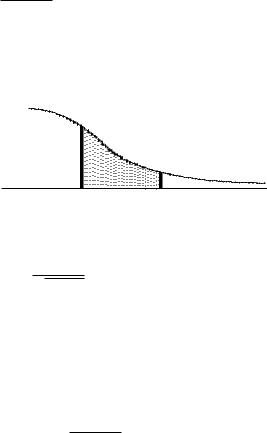
2209.

∫

√

dx

.

1 x2

−

1/2

−

6y

−1	/q 2				O	1		/q 2	-x

Рис. 3.4

76

1/2

1/2

∫

dx

π

π

π

−

= 6

+ 6

= 3 .

√1 x2

1/2

= arcsin x

−

1/2

−

sh 2

2210.

∫

√

dx

.

1 + x2

sh 1

6y

q

q

-

O

shq

1

shq

2

x

∫sh 2

√ dx

1 + x2

sh 1

Рис. 3.5

					sh 2
= ln(x +		√1 + x2 ) sh 1 .
√

Так как функция y = ln(x+ 1 + x2 ) является обратной к функции x = sh y, то

ln(x + √1

+ x2 ) x=sh 1

= 1 ,

ln(x +

√1 + x2 ) x=sh 2

= 2,

и поэтому

sh 2

∫

√

dx

= 2 − 1 = 1.

1 + x2

sh 1

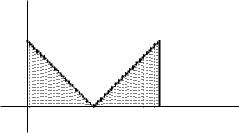
2211.

∫02

|1

− x| dx.

77

6y

O	1q	2q	-x
		Рис. 3.6

∫2 ∫1 ∫2 ∫1

|1 − x| dx = |1 − x| dx + |1 − x| dx = (1 − x) dx+

0 0 1 0

2			x2			1			x2		2		1	1
1
+ ∫ (x − 1) dx = (x −			2		) 0		+	(	2	− x) 1		=	2	+	2	= 1.
	1
2212.	∫	dx				(0 < α < π).
		x2 − 2x cos α + 1
	−1

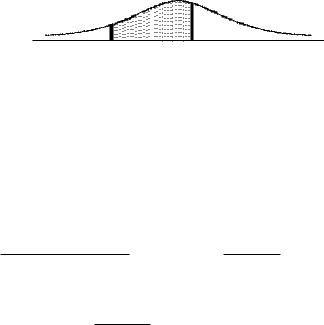
Подынтегральную функцию можно представить в виде

f(x) =	1	=	1	,
	x2 − 2x cos α + 1		(x − cos α)2 + sin2 α

ее график представлен на рис. 3.7.

78

q

6y

q

-

−

q1

O

cos αq

q

1

x

Рис. 3.7

1

1

∫

dx

= ∫

dx

=

x2

−

2x cos α + 1

(x

−

cos α)2 + sin2 α

−

1

−

1

1

d(x − cos α)

1

x − cos α

1

=

=

arctg

=

−

∫

(x

cos α)2

+ sin2 α

sin α

sin α

−

1

1

−

=

1

arctg

1 − cos α

+ arctg

1 + cos α

=

sin α

sin α [

sin α

]

1

α

α

=

[arctg tg

+ arctg ctg

] =

sin α

2

2

= sin α [

2 + (

2 − 2 )]

=

2 sin α.

1

α

π

α

π

2π

2213.

∫0

dx

(0 6 ε < 1).

1 + ε cos x

79

1−ε

6y

q

q

1

q

q

q

1

1

2q

πq

32q

2qπ

O

1+ε

q

q

-x

π

π

Рис. 3.8

а). При ε = 0

2π

2π

∫0

dx

= ∫0

dx = 2π.

1 + ε cos x

б). При 0 < ε < 1 неопределенный интеграл вычислен в за-

даче 2028,а:

∫

2

(√

dx

=

arctg

1 − ε

tg

x

+ C.

1 + ε cos x

√1 − ε2

1 + ε

2 )

Первообразная имеет разрыв при x = π, поэтому для применения формулы Ньютона – Лейбница, определенный интеграл надо разбить на два:

2π

π

2π

∫0

dx

∫0

dx

∫π

dx

=

+

=

1 + ε cos x

1 + ε cos x

1 + ε cos x

√1 ε2

(√1 + ε

2 )

π

−

0

=

2

arctg

1 − ε

tg

x

+

2π

)

√

(√

1 + ε

2

1

−

ε2

+

2

arctg

1 − ε

tg x

=

80