Орловский Определенный интеграл.Практикум ч.1 2010

+

ax + b

+∞

= [2(n

∞

+

−

1)∆(ax2 + 2bx + c)n−1 ]

∫

−∞

+

(2n − 3)a

dx

=

(2n − 3)a

I

.

2(n − 1)∆

(ax2 + 2bx + c)n−1

2(n − 1)∆

n−1

−∞

Это приводит к рекуррентному соотношению

I

n

=

(2n − 3)a

I

n−1

.

(2n − 2)∆

Применяя полученное соотношение n − 1 раз, находим:

In

=

(2n − 3)a(2n − 5)a . . . 3a · a

I1 =

(2n − 2)∆(2n − 4)∆ . . . (4∆)(2∆)

=

(2n − 3)!!

(

a

)

n−1

I

.

(2n − 2)!!

∆

1

Так как ac − b2 > 0, то после замены y = x + ab

имеем:

b

+∞

dx

+∞

d (x +

)

a

I1 = ∫

= ∫

=

ax2 + 2bx + c

a x +

b

2 +

ac − b2

a)

−∞

−∞

(

a

1

+∞

du

1

[

a

au

]

+

∞

∫

=

=

√

arctg

√

=

a

ac

b2

a

2

ac

b2

ac

b2

−∞

u

+

−

−

−

−∞

2

a

π sgn a

= √

.

Следовательно,

ac − b2

+∞

dx

=

(2n − 3)!!πan−1 sgn a .

∫

(ax2 + 2bx + c)n

(2n

−

2)!!(ac

−

b2)n−21

−∞

241

	+∞
2350. In = ∫		dx					.
		x(x + 1) . . . (x + n)
1
Разложим подынтегральную функцию на элементарные дро-
би
1			=	c0	+		c1	+ · · · +	cn
										.
	x(x + 1) . . . (x + n)			x		x + 1			x + n

Приводя к общему знаменателю и освобождаясь от него, получаем тождество

1= c0(x + 1) . . . (x + n) + · · ·

·· · + ckx(x + 1) . . . (x + k − 1)(x + k + 1) . . . (x + n) + · · ·

·· · + cnx(x + 1) . . . (x + n − 1).

Полагая в этом тождестве x= −k и учитывая, что все слагаемые в правой части кроме k-го (слагаемые нумеруются с нуля) равны нулю, имеем:

1 = ck(−k)(−k + 1) . . . (−1)(1)(2) . . . (n − k),

откуда находим

ck =

(−1)k

=

(−1)kCnk

.

k!(n − k)!

n!

Следовательно,

= 1

(−1)kCnk .

1

n

∑

x(x + 1) . . . (x + n)

n!

k=0

x + k

Интегрируя это равенство, получаем

∫

x(x + 1) . . . (x + n)

= [n! k=0(−1)kCnk ln(x + k)]1

=

+∞

n

+∞

1

dx

1

∑

242

=

1

lim

n

(

1)kCk ln(x + k)

1

n

( 1)kCk ln(k + 1).

n! x

−

− n!

→

+

∞

k=0

n

k=0

−

n

∑

∑

Из формулы бинома Ньютона следует, что

n

(−1)kCnk = (1 − 1)n = 0,

k=0

∑

Поэтому

n

(−1)kCnk ln(x + k) =

k=0

n

∑

n

(−1)kCnk)ln(x) =

= (−1)kCnk ln(x + k) − (

k=0

k=0

n

∑

∑

n

x + k

= (−1)kCnk (ln(x + k) − ln(x)) =

(−1)kCnk ln

.

x

k=0

k=0

∑

∑

Таким образом,

n

n

x + k

lim

( 1)kCk ln(x + k) =

( 1)kCk

lim

ln

= 0

x→+∞

−

n

−

n x→+∞

x

k=0

k=0

∑

∑

и искомый интеграл

+∞

dx

1

n

∫

= −

k=0(−1)kCnk ln(k + 1) =

x(x + 1) . . . (x + n)

n!

1

∑

1

n

1

n

=

(−1)k+1Cnk ln(k + 1) =

(−1)k+1Cnk ln(k + 1)

n!

n!

k=0

k=1

∑

∑

(слагаемое, отвечающее k = 0, равно нулю).

1

n dx

2351. In = ∫

x

.

(1

x)(1 + x)

0

√

−

243

Замена t = arcsin x (x = sin t) дает

π/2

In = ∫0

sinn t dt.

Согласно решению задачи 2882

(2k − 1)!!

·

π

,

n = 2k,

(2k)!!

2

In =

(2k)!!

+

∞

, n = 2k + 1.

2352. In = ∫0

(2k + 1)!!

dx

.

chn+1 x

Используя свойства гиперболических функций и интегрируя

по частям, получаем:

+∞

2 x sh2 x

+∞ sh2 x

In = ∫0

ch −

dx = In−2 − ∫0

dx =

chn+1 x

chn+1 x

1

+∞

(

1

) = In−2 +

∫0

= In−2 +

sh x d

n

chn x

1

sh x

+∞

+∞

dx

0

−

∫

+ n chn x

0

chn−1 x =

1

n

−

1

= I

n−2

+

[0

−

I

] =

I

.

n

n

n−2

n−2

Таким образом, для рассматриваемого интеграла имеет место рекуррентное соотношение

n − 1

In = n In−2.

244

Нетрудно вычислить интегралы при n = 0 и n = 1:

+∞			+∞	d(sh x)
I0 = ∫	dx	=	∫		=
	ch x			ch2 x

00

+∞

(sh x)

+

∞

π

= ∫

= arctg(sh x) 0

d

=

.

1 + sh2 x

2

0

+∞

dx

+

I1 = ∫

= th x 0

∞

= 1.

ch2 x

0

Далее воспользуемся рекуррентным соотношением. При n =

= 2k применим рекуррентное соотношение k раз, получаем

In = I2k =

2k − 1

I2k−2 = . . . =

(2k − 1)(2k − 3) . . . 3 · 1

I0 =

2k

(2k)(2k − 2) . . . 4 · 2

=

(2k − 1)!!

π

= (n − 1)!!

π .

(2k)!!

·

2

n!!

·

2

При n = 2k + 1 применим рекуррентное соотношение k раз:

In = I2k+1 =

2k

= . . .

I2k−1

2k + 1

. . . =

(2k)(2k − 2) . . . 4 · 2

I

=

(2k)!!

1 =

(n − 1)!!

.

(2k + 1)(2k − 1) . . . 5 · 3

1

(2k + 1)!! ·

n!!

Следовательно,

(n − 1)!!

·

π

,

n

– четное

,

I

=

n!!

2

n

(n

1)!!

−

,

n

– нечетное

.

n!!

π/2

π/2

2353. а)

∫0

ln sin x dx;

б)

∫0

ln cos x dx.

245

Пусть

π/2		π/2
I1 = ∫0	ln sin x dx ,	I2 = ∫0	ln cos x dx.

Покажем, что I1 = I2, для этого в I2 сделаем замену x = π2 − t:

0				π/2
I2 = − ∫	ln cos	π	− t dt =	∫	ln sin t dt = I1.
		2
π/2	(		)	0

Обозначим общее значение этих интегралов через I. Тогда

					π/2				π/2
2I = I1 + I2 = ∫0						ln sin x dx + ∫0				ln cos x dx =
π/2								π/2
= ∫0	[ln sin x + ln cos x] dx = ∫0								ln (sin x cos x) dx =
	π/2						π/2
= ∫0		ln	sin 2x		dx =		∫0	[ln sin 2x − ln 2] dx =
			2

∫π/2

=ln sin 2x dx − π2 ln 2.

0

Преобразуем интеграл в правой части последнего равенства, делая замену 2x = t:

	π/2		1	π	1	π/2		1	π
	∫	ln sin 2x dx =		∫ ln sin t dt =		∫	ln sin t dt +		∫	ln sin t dt.
			2		2			2
	0			0		0			π/2

246

Если во втором из полученных интегралов сделать замену z = π − t, получим

∫π ln sin t dt = − ∫0

π/2

ln sin(π − z)dz = ∫

ln sin z dz.

π/2

π/2

0

Следовательно,

π/2

1

π/2

1

π/2

1

1

∫0

ln sin 2x dx =

∫0

ln sin t dt +

∫0 ln sin z dz =

I +

I = I,

2

2

2

2

что приводит к уравнению

2I = I

−

π

ln 2.

2

Решая полученное уравнение, находим:

π

I = −

ln 2,

2

т. е.

π/2

π/2

∫0

ln sin x dx = ∫0

ln cos x dx = −

π

ln 2.

2

2354. Найти

∫

e

−

x/2

|

sin x − cos x|

dx,

√sin x

E

где E – множество тех значений x интервала (0; +∞), для которых подынтегральное выражение имеет смысл.

Прежде всего, вычислим неопределенный интеграл от подынтегральной функции с опущенным знаком модуля:

∫	e	−	x/2	sin x − cos x			dx =
				√sin x

247

cos x

= ∫ (e−x/2√sin x − e−x/2

)dx =

√

= ∫

sin x

(

)

−2e−x/2√

sin x

′ dx = −2e−x/2

√

sin x

+ C.

Область определения подынтегральной функции

∞

n

(2πn; π + 2πn)

E =

=0

и рассматриваемый интеграл

π+2πn

∫

e

−

x/2 | sin x − cos x|

dx =

∞

∫

e

−

x/2

|

sin x − cos x|

dx.

√sin x

n=0

√sin x

E

∑

2πn

На

промежутке [2πn; π/4 +

2πn]

модуль

| sin x − cos x| =

= −(sin x − cos x), а на участке [π/4 + 2πn; π + 2πn] величина | sin x − cos x| = sin x − cos x. Следовательно, учитывая найденный выше неопределенный интеграл, имеем:

π+2πn

sin x − cos x| dx =

(

)

π/4+2πn

2πn

x/2

e

2e

x/2√sin x

∫

−

|

√sin x

−

−

π+2πn

√4

− (2e−x/2√sin x) π/4+2πn = 2

8 e−π/8e−πn.

Таким образом,

∞

E

∑

∫

e

−

x/2

|

sin x − cos x|

dx = 2

√4 8 e

−

π/8

e

−

πn.

√sin x

n=0

Суммируя геометрическую прогрессию, находим:

∞

∞

)

−

∑

∑ (

e−πn =

e−π

n =

1

1

e−π

n=0

n=0

248

и искомый интеграл

sin x − cos x|

2

√4

e−π/8

.

e

−

x/2

|

dx =

8

∫

√sin x

1

−

e−π

E

2355. Доказать равенство

+∞

b

1

+∞

(√

)

0

0

∫

f(ax +

)dx =

∫

f

x2 + 4ab dx,

x

a

где a > 0 и b > 0, предполагая, что интеграл в левой части равенства имеет смысл.

Рассмотрм на положительной полуоси функцию

y = ax +

b

,

x

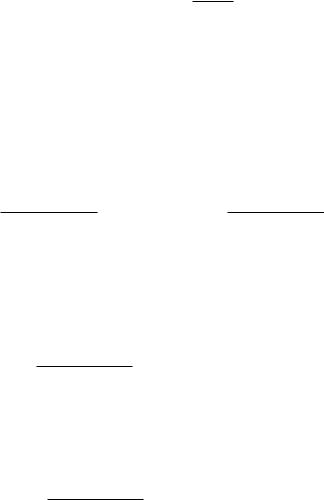
график которой представлен на рис. 5.1.

y

6

y = ax +

b

√

x

q

2 ab

bq

-x

O

√a

Рис. 5.1

Он имеет асимптоты x = 0 и y = ax. В точке x =

b/a

функция имеет единственный экстремум

y = 2

√

,

являющийся

ab

√

строгим минимумом. На промежутках (0;

√

] и [√

; +∞)

b/a

b/a

249

эта функция имеет обратные, которые обозначим, соответственно, x1(y) и x2(y). Их явный вид легко найти, решая уравнение

y = ax + xb

относительно переменной x. Приводя к общему знаменателю, получаем квадратное уравнение ax2 − yx + b = 0. Решая его, находим:

y

y2

4ab

y + y2

4ab

x1(y) =

− √2a −

, x2

(y) =

√2a

−

.

Рассматриваемый интеграл разбиваем на два:

√

+∞

b/a

+∞

b

b

b

∫ f(ax +

)dx = ∫

f(ax +

)dx + ∫

f(ax +

)dx.

x

x

x

0

0

√

b/a

В первом интеграле сделаем подстановку x = x1(y), а во втором – замену x = x2(y). В обоих случаях ax + b/x = y (по определению обратной функции). После замены получаем:

√

2√

b/a

b

ab

∫

f(ax +

)dx = ∫ f(y)x1′ (y)dy =

x

0

2√

+∞

(1 −

)dy =

ab

=

1

∫ f(y)

y

2a

y2

4ab

+

∞

−

(

√

− 1)dy.

+

=

1

∫∞ f(y)

y

2a

√

y2 4ab

2√

−

ab

+∞

b

+∞

∫

f(ax +

)dx = ∫ f(y)x2′ (y)dy =

x

√

2√

b/a

ab

250