
[ Филиппов ] Теория упругости (лекции)
.pdfН. Н. Филиппов
ОБЩАЯ ФИЗИКА
ВВЕДЕНИЕ В МЕХАНИКУ СПЛОШНЫХ СРЕД
ТЕОРИЯ УПРУГОСТИ
2
ОГЛАВЛЕНИЕ
1.ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНЫХ СРЕД ………… 4
2.ОСНОВЫ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ ……………………….. 4
2.1.Эмпирические основы линейной теории упругости ………………… 4
2.2.Качественные характеристики деформации стержня ……………….. 5
2.3.Закон Гука ……………………………………………………………… 5
2.4.Изменение диаметра стержня ………………………………………… 6
2.5.Изменение объема стержня ………………………………………….. 7
2.6.Дифференциальная форма закона Гука ……………………………… 7
2.7.Принцип суперпозиции ……………………………………………….. 8
2.8.Пределы применимости теории упругости ………………………….. 8
3.ОДНОРОДНЫЕ ДЕФОРМАЦИИ ………………………………………... 9
3.1.Гидростатическое давление …………………………………………... 9
3.2.Продольная деформация при запрещенных боковых смещениях … 10
3.3.Деформация сдвига …………………………………………………... 11
4.НЕОДНОРОДНЫЕ ДЕФОРМАЦИИ …………………………………… 15
4.1.Деформация под действием массовых сил ………………………… 16
4.2.Деформация кручения ………………………………………………... 18
4.2.1.Кручение тонкостенного цилиндра …………………………... 18
4.2.2.Толстостенная трубка …………………………………………. 20
4.2.3.Сплошной цилиндр ……………………………………………. 20
4.2.4.Кручение как неоднородная деформация ……………………. 20
4.2.5.Изменение объема тела при кручении ……………………….. 21
4.2.6.Крутильные весы ………………………………………………. 21
4.2.6.Крутильный маятник ………………………………………….. 22
4.3.Деформация изгиба …………………………………………………... 23
4.3.1.Изгиб балки …………………………………………………….. 23
4.3.2.Жесткость балки ……………………………………………….. 25
4.3.3.Прогиб консольной балки …………………………………….. 26
4.3.4.Колебания нагруженной балки ……………………………….. 27
4.3.5.Перерезывающая сила ………………………………………… 29
4.3.6.Устойчивость упругого равновесия ………………………….. 30
5.ВОЛНОВЫЕ ЯВЛЕНИЯ В УПРУГИХ СРЕДАХ ……………………… 33
5.1.Продольные волны в стержне …………………………………….…. 33
5.1.1.Волновое уравнение …………………………………….….….. 33
5.1.2.Звуковые волны в тонком стержне …………………….……... 35
5.2.Волны в тонких пластинах …………………………………….…..… 36
3
5.3.Волны в неограниченных упругих средах …………………………. 38
5.3.1.Продольные волны ……………………………………………. 38
5.3.2.Поперечные волны ……………………………………………. 39
5.4Скорости распространения упругих волн ………………………….. 40
5.5.Крутильные волны в стержнях ……………………………………… 40
5.6.Волны изгиба в стержнях ……………………………………………. 42
5.7.Собственные колебания стержней …………………………………... 44
6.ОСНОВЫ ОБЩЕЙ ТЕОРИИ УПРУГОСТИ …………………………… 49
6.1.Тензор напряжений …………………………………………………... 49
6.2.Тензор деформаций …………………………………………………... 49
6.3.Обобщенный закон Гука ……………………………………………... 50
ЗАДАЧИ ……………………………………………………………………... 50
ЛИТЕРАТУРА ………………………………………………………………. 51
4
1. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНЫХ СРЕД
Основные объекты теоретической механики
•Материальная точка
•Дискретные системы материальных точек
•Абсолютно твердые тела
Основные объекты механики сплошных сред
•Газообразные среды
•Жидкие среды
•Твердые деформируемые тела
Характеристики сплошных сред
•Однородность (неоднородность) относительно некоторого свойства
•Изотропность (анизотропность) относительно некоторого свойства
Типы сил в механике сплошных сред
•Массовые силы действуют на все элементы сплошной среды.
•Поверхностные силы действуют на элемент поверхности, ограничивающей тело, или ограничивающей внутренний элемент среды.
Основные разделы механики сплошных сред
•Теория упругости – изучение деформаций и возникающих при этом напряжений в твердых телах.
•Гидродинамика – изучение законов движения жидкостей и газов.
2.ОСНОВЫ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
2.1.Эмпирические основы линейной теории упругости
•Атомно-молекулярная структура тел, определяющая их упругое поведение, не рассматривается механикой сплошных сред.
•Основные законы упругого поведения твердых тел получены из двух экспериментальных фактов:
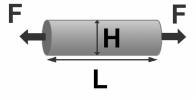
Малые удлинения (сокращения) δL
стержня (Рис. 1) пропорциональны приложенной силе: δL F .
При растяжении (сжатии) стержня его
диаметр |
H |
|
уменьшается |
|
(увеличивается): |
δH |
− |
Рис. 2.1 |
|
δL . |
||||
|
|
H |
|
L |
5
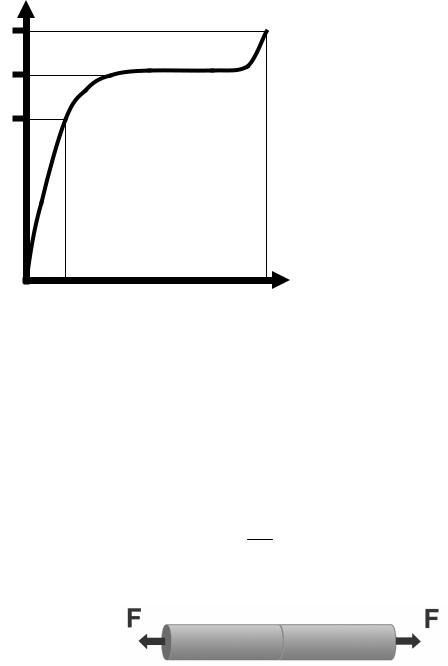
2.2.Качественные характеристики деформации стержня
F
Fs
Ff
Fe
0
Рис. 2.2. Зависимость удлинения стержня от приложенной силы. Fe – предел упругости (при
F < Fe |
удлинение |
|
является |
|
обратимым), Ff |
– |
предел |
||
текучести, |
Fs |
– |
предел |
|
прочности. |
|
|
|
|
δL
Линейная теория упругости справедлива при малых удлинениях δL , вызываемых силами F << Fe .
2.3.Закон Гука
Деформация ε - относительное изменение размеров тела: ε = δLL .
Для стержня удвоенной (Рис. 3) длины L′= 2L удлинение под действием силы F также составляет удвоенную величину δL′= 2 δL . Деформация при
этом остается неизменной: ε′= δLL′′ = δLL = ε. Деформация в этом случае зависит только от приложенной силы: ε F .
Рис. 2.3
Напряжение σ - отношение силы F к площади сечения S : σ = FS .
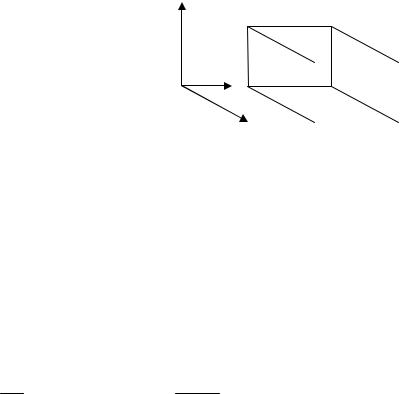
Для стержня удвоенного (Рис. 4) сечения S′= 2S деформация сохраняется при удвоенной величине приложенной силы F′= 2F . Напряжение при
этом остается неизменным: σ′= FS′′ = FS = σ. Вне зависимости от длины и сечения стержня, его деформация пропорциональна напряжению:

6 |
|
||
ε = |
σ |
- закон Гука |
|
|
|
||
|
E |
|
|
E – коэффициент пропорциональности, |
Рис. 2.4 |
||
называемый модулем Юнга. Модуль Юнга |
|||
является характеристикой вещества, из которого сделано исследуемое тело. В таблице 1 для некоторых веществ приведены значения модуля
Юнга, напряжения σe = FSe , характеризующего предел упругости, и
величины максимальной упругой деформации εmax = σEe .
Таблица 1. Модуль Юнга, предел упругости, максимальная упругая деформация и коэффициент Пуассона.
Материал |
E |
σe |
εmax |
ν |
|
1010 Н/м2 |
107 Н/м2 |
0,003 |
|
Сталь |
20 |
60 |
0,26 |
|
Железо |
13 |
5 |
0,0004 |
0,26 |
Медь |
11 |
3 |
0,0003 |
0,37 |
Олово |
4 |
0,33 |
0,00008 |
0,33 |
Свинец |
1,6 |
0,24 |
0,00015 |
0,45 |
В теории упругости рассматриваются деформации ε<< εmax , поэтому с полным основанием можно считать | ε|<<1 и строить теорию в линейном по ε приближении.
2.4.Изменение диаметра стержня
Относительное изменение диаметра (Рис. 1) стержня ε пропорционально
его продольной деформации: ε = |
δH |
= −ν |
δL |
= −νε, |
где ν > 0 - |
|
H |
L |
|||||
|
|
|
|
коэффициент Пуассона. С учетом закона Гука, формула для поперечной деформации стержня приобретает вид:
ε = − Eν σ
Значения коэффициента Пуассона для ряда веществ приведены в таблице 1.

7
2.5.Изменение объема стержня
Объем стержня до деформации: V = π4 H 2L .
Объем деформированного стержня: V ′= π4 (H +δH )2 (L +δL).
Изменение объема в результате деформации: δV =V ′−V .
Относительное изменение объема: δV = (H +δH )2 (L2+δL)− H 2 L .
V H L
С учетом малости деформаций: δVV = ε+2ε +2ε ε+ε2 +ε2 ε ≈ ε+2ε .
Учитывая связь деформаций и напряжения: δVV = 1−E2 νσ.
Из физических соображений следует, что при растяжении стержня его объем не может уменьшаться, поэтому 1−E2 ν > 0. Последнее соотношение
позволяет уточнить область значений коэффициента Пуассона: 0 < ν < 12 .
Чем ближе значение ν к 12 , тем меньше относительное изменение объема стержня при данном приложенном напряжении.
2.6.Дифференциальная форма закона Гука
Малый интервал:
∆x = x2 − x1
После деформации:
x1′ = x1 +u(x1) x2′ = x2 +u(x2 )
Функция u(x) - величина
смещения точек бруска в результате его деформации
Длина интервала после деформации
∆x′ = x′2 − x1′ =[x2 +u(x2 )]−[x1 +u(x1)]
∆x′ = x2 − x1 |
+u(x2 ) −u(x1) |
Рис. 2.5 |
|||||
′ |
|
u |
(x2 ) |
−u(x1) |
|
||
= ∆x + |
∆x |
|
|||||
∆x |
|
|
∆x |
|
|||
|
|
∂u |
|
|
|||
′ |
≈ ∆x + |
∆x |
|
|
|
||
∆x |
∂x |
|
|
|
|||

8
Изменение длины интервала ∆x : δ(∆x) = ∆x′− ∆x ≈ ∂∂ux ∆x Деформация элемента ∆x : ε = δ(∆∆xx) ≈ ∂∂ux
Из закона Гука: ε = Eσ
Дифференциальная форма закона Гука: ∂u = σ(x)
∂x E(x)
2.7.Принцип суперпозиции
Если под действием некоторой силы Fi тело испытывает деформацию εi , то совокупное действие таких сил F = ∑Fi приведет к деформации
i
ε = ∑εi .
i
2.8.Пределы применимости теории упругости
Процессы необратимой пластической деформации в нагруженном твердом теле протекают всегда. При малых напряжениях такие деформации являются пренебрежимо малыми, если нагрузка действует в течение относительно небольшого интервала времени. В этом случае мы можем говорить, что деформация тела является упругой. При увеличении длительности нагруженного состояния остаточная деформация после снятия нагрузки может оказаться существенной, и деформация тела теряет свойство упругости. Если сохранять тело в нагруженном состоянии достаточно долго, даже небольшие напряжения могут привести к его разрушению. Время, которое образец может выдержать под нагрузкой до разрушения, называется его долговечностью. В большом диапазоне напряжений средняя долговечность тел τ хорошо описывается выражением
τ= exp U − γσ ,
kT
где U и γ являются эмпирическими параметрами, зависящими от материала образца, Т - абсолютная температура, k - постоянная Больцмана. Изучением процессов, определяющих долговечность тел, занимается кинетическая теория прочности.
9
Лекция 2
3. ОДНОРОДНЫЕ ДЕФОРМАЦИИ
Однородными называются такие деформации, при которых величина
ε = ∂∂ux постоянна по всему телу. Ниже мы рассмотрим несколько примеров однородных деформаций.
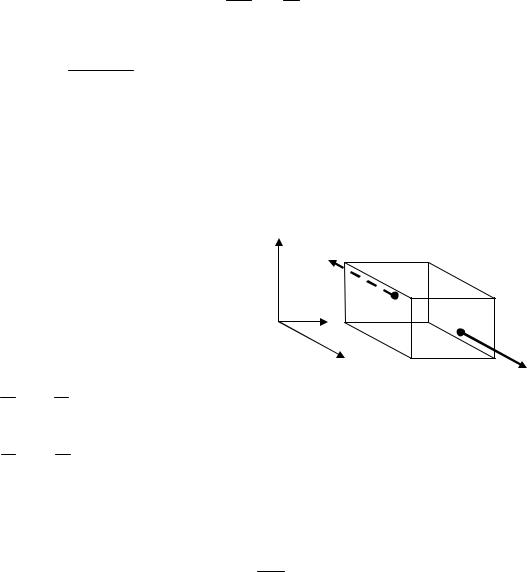
3.1.Гидростатическое давление
Брусок (параллелепипед) помещен в жидкость с постоянным давлением, рассмотрим изменение его размеров, исходя из принципа суперпозиции.
Начнем с анализа деформации бруска в направлении x (Рис. 3.1). Эта |
|||||||
деформация будет складываться из следующих составляющих: |
|||||||
1. |
деформации продольного сжатия εx1 |
z |
|
|
ly |
||
|
за счет давления на переднюю и |
|
|
|
|
lx |
|
2. |
заднюю грани бруска. |
|
y |
|
|
||
деформации удлинения εx2 за счет |
|
|
lz |
||||
|
|
||||||
|
давления на верхнюю и нижнюю |
|
|
|
|
|
|
|
грани бруска; |
|
|
|
|
|
|
3. |
деформации удлинения εx3 за счет |
|
|
x |
|
||
|
давления на правую и левую грани |
|
|
|
Рис. 3.1 |
||
|
|
|
|
||||
бруска; |
|
|
|
|
|
||
Внешняя сила, действующая |
на |
единицу |
|
поверхности бруска |
|||
(напряжение), равна давлению жидкости P , поэтому |
|
||||||
εx1 = − |
P |
; εx2 |
= |
ν |
P ; εx3 = |
ν |
P , |
|
E |
E |
|||||
|
E |
|
|
|
|||
а общая деформация находится простым суммированием:
εx = δllxx = εx1 + εx2 + εx3 = −1−E2ν P .
Всилу симметрии задачи (направление x не является физически выделенным), получаем
δl |
z = |
δly |
= |
δl |
x = − |
1 |
− 2ν |
P . |
lz |
ly |
|
|
E |
||||
|
|
lx |
|
|
||||
Этот результат позволяет легко вычислить и относительное изменение
10
объема бруска V . Исходный объем был равен V =lx ly lz , а изменение объема под действием внешних сил составило
δV = (lx + δlx )(ly + δly )(lz + δlz )−lx ly lz .
Раскрывая скобки и оставляя линейные по малым параметрам δl члены, получаем
δV =ly lz δlx +lz lx δly +lx ly δlz ,
откуда следует
δV |
= |
δl |
x + |
δly |
+ |
δl |
z = −3 |
1 |
− 2ν |
P , |
V |
|
ly |
|
|
E |
|||||
|
lx |
|
lz |
|
|
|||||
или
δVV = − KP ,
где
K= 3(1−E2ν) - модуль всестороннего объемного сжатия
3.2.Продольная деформация при запрещенных боковых смещениях
Брусок (параллелепипед) испытывает продольную деформацию под
действием внешнего напряжения σx |
(рис. 3.2). Рассмотрим изменение его |
|||||||||||||||
длины lx |
при запрещенных смещениях боковых граней, перпендикулярных |
|||||||||||||||
направлению |
|
y |
( εy = 0 ). |
Грани, |
z |
σx |
ly |
|||||||||
перпендикулярные направлению z, |
||||||||||||||||
остаются |
|
при |
|
|
этом |
свободными |
|
|
lx |
|||||||
( σz = 0 ). Величину деформации εx |
|
y |
|
|||||||||||||
при данных условиях можно найти |
|
|
lz |
|||||||||||||
из следующих уравнений: |
|
|
|
|||||||||||||
|
|
|
σx |
|||||||||||||
|
|
|
1 |
|
|
|
ν |
|
|
|
|
|
|
|
x |
|
εx |
= |
σx |
− |
σy ; |
|
|
|
|
Рис. 3.2 |
|||||||
|
|
|
|
|
||||||||||||
|
|
|
E |
|
|
|
E |
|
|
|
|
|
|
|
|
|
ε |
y |
= |
1 |
σ |
y |
− |
ν |
σ |
x |
= 0, |
|
|
|
|
|
|
|
|
E |
|
|
E |
|
|
|
|
|
|
|
|
|||
откуда следует σy = νσx и |
|
|
|
|
||||||||||||
εx = E1эф σx ,
