Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Интегрированные системы управления и проектирования

Файл:

Березкин Основы теории информации и кодирования Лабораторный практикум 2009

.pdf

Скачиваний:

238

Добавлен:

17.08.2013

Размер:

715.03 Кб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)

____________________________________________

Е.Ф. Березкин

ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ И КОДИРОВАНИЯ

Лабораторный практикум

Учебно-методическое пособие 2-е издание, переработанное и дополненное

Москва 2009

УДК 519.72(076.5) ББК 22.18я 7 Б48

Березкин Е.Ф. Основы теории информации и кодирования. Лабо-

раторный практикум: Учебно-методическое пособие. – 2-е изд., пере-

раб. и доп. – М.: МИФИ, 2009. – 84 с.

Приведены описания восьми лабораторных работ. Первые четыре работы посвящены исследованию математических моделей непрерывных сигналов, следующие четыре – исследованию информационных моделей дискретных сигналов. Все работы выполняются в дисплейном классе на IBM совместных ПЭВМ с использованием специализированного компьютерного учебника ОТИК 4.15.

Лабораторный практикум предназначен для студентов, обучающихся по специальности 230102 «Автоматизированные системы обработки информации и управления» и направлению подготовки бакалавров и магистров 230100 «Информатика и вычислительная техника».

Рецензент д-р техн. наук, проф. Ю.Г. Древс

Рекомендовано редсоветом МИФИ

в качестве учебно-методического пособия

ISBN 978-5-7262-1120-6 © Московский инженерно-физический институт (государственный университет), 2009

Редактор Е.Е. Шумакова Оригинал-макет изготовлен Е.Ф. Березкиным

Подписано в печать 16.02.2009. Формат 60х84 1/16.

Печ.л. 5,25. Уч.-изд.л. 5,25. Тираж 150 экз.

Изд. № 030-1. Заказ №

_______________________________________________________________________

Московский инженерно-физический институт (государственный университет),

115409, Москва, Каширское шоссе, д.31. Типография МИФИ.

ОГЛАВЛЕНИЕ

_______________________________________________________________

Предисловие ........................................……………………………..........	4
Лабораторная работа 1. Математические модели детерминированных
периодических сигналов .............……………….……….......	5
Лабораторная работа 2. Математические модели детерминированных
непериодических сигналов .......…………………………......	13
Лабораторная работа 3. Дискретизация непрерывных сигналов ……..	23
Лабораторная работа 4. Математические модели случайных сигналов
и элементы теории оптимального приема .….…….…….......	36
Лабораторная работа 5. Рациональное кодирование двоичного
источника .…………………………………………………......	44
Лабораторная работа 6. Исследование информационной пропускной
способности двоичного канала .……..………............…….....	54
Лабораторная работа 7. Корректирующие коды
Боуза–Чоудхури–Хоквингема .…………………………….…	62
Лабораторная работа 8. Построение кодирующих и декодирующих
устройств циклического кода Хэмминга ………………........	71
Список рекомендуемой литературы ..........……………........…….........	82
Приложение ………………………………………………………………	83

_______________________________________________________________

ПРЕДИСЛОВИЕ

Курс «Основы теории информации и кодирования» читается студентам III курса (5-й и 6-й семестры) кафедры «Управляющие интеллектуальные системы». Лабораторный практикум по курсу выполняется в дисплейных классах кафедры с использованием специализированного компьютерного учебника ОТИК 4.15 нового поколения, который состоит из единого программного комплекса и предназначен для самостоятельного выполнения практических заданий и решения задач, охватывающих все разделы курса.

Первое издание учебного пособия (Березкин Е.Ф., Федосеев Ю.Н. Лабораторный практикум по курсу "Основы теории информации и кодирования". – М.: МИФИ, 1997), базировавшегося на компьютерном учебнике ОТИК предыдущего поколения, существенно переработано и дополнено новыми работами.

Программный комплекс – диалоговая программа с оверлейной структурой, позволяющая детальнее и глубже изучить соответствующий материал и содержащая специальные средства, с помощью которых можно провести достаточно интересные и серьезные исследования. Как правило, специальные средства обеспечивают автоматизацию наиболее трудоемких процедур проектирования информационной техники.

Практические задания разработаны для изучения: математических моделей детерминированных периодических сигналов; математических моделей детерминированных непериодических сигналов; дискретизации непрерывных сигналов по времени; математических моделей случайных сигналов и элементов теории оптимального приема; рационального кодирования двоичного источника; информационной пропускной способности двоичного канала; корректирующих кодов Боуза–Чоудхури–Хоквингема; кодирующих и декодирующих устройств циклического кода Хэмминга заданной канальности.

Программный комплекс разработан на алгоритмическом языке

Delphi 7.0 с использованием HTML Help Workshop 1.3 и занимает на HDD порядка 30 Mb. Дистрибутив комплекса реализован с по-

мощью InstallShield Express 2.12.

Лабораторная работа 1

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЕТЕРМИНИРОВАННЫХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Цель: изучение и исследование спектральных характеристик детерминированных периодических сигналов.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Теория анализа и обработки физических данных базируется на математических моделях соответствующих физических полей и физических процессов, на основе которых создаются математические модели сигналов. Математические модели сигналов дают возможность обобщенно, абстрагируясь от физической природы, судить о свойствах сигналов, предсказывать изменения сигналов в изменяющихся условиях, заменять физическое моделирование процессов математическим. С помощью математических моделей имеется возможность описывать свойства сигналов, которые являются главными, определяющими в изучаемых процессах, и игнорировать большое число второстепенных признаков. Знание математических моделей сигналов дает возможность классифицировать их по различным признакам, характерным для того или иного типа моделей.

Сигнал – изменяющаяся физическая величина, обеспечивающая передачу информации по линии связи. Сигналы, используемые в информационных системах, можно разделить на две группы: детерминированные и случайные сигналы. Детерминированные сигналы характеризуются тем, что в любые моменты времени их значения являются известными величинами, а случайные – тем, что их значения в любые моменты времени – случайные величины.

Деление сигналов на детерминированные и случайные условно, так как детерминированных сигналов в точном их понимании в природе нет. На практике нельзя точно предсказать значение сигнала в любые моменты времени, в противном случае сигнал не нес бы полезной информации. Кроме того, любой реальный сигнал

случаен в силу воздействия на него многочисленных случайных факторов.

Несмотря на это, исследование детерминированных сигналов весьма важно, так как выводы, полученные в результате анализа периодических и непериодических детерминированных сигналов, во многих случаях можно использовать для анализа случайных сигналов.

Важнейшая характеристика сигнала – его частотные свойства. Для исследования используется частотное представление функции в виде спектра, являющегося преобразованием Фурье временной формы. В процессе переработки и передачи сигналов эта характеристика играет особую роль, так как определяет параметры используемой аппаратуры.

При разложении периодического колебания x(t) в ряд Фурье

по тригонометрическим функциям в качестве ортогональной системы берут

1,cosω0t,sinω0t,cos2ω0t,sin2ω0t,...,coskω0t,sinkω0t,... (1.1)

или

..., e− j 2 ω0t , e− jω0t ,1, e jω0t , e j 2 ω0t ,... .

(1.2)

Интервал ортогональности в обоих случаях совпадает с перио-

домT = 2π/ ω0 функции x(t) .

Система функций (1.1) приводит к тригонометрической форме ряда Фурье, а система (1.2) – к комплексной форме. Между этими двумя формами существует простая связь.

Тригонометрическая форма ряда Фурье имеет вид:

∞

x(t) =

+ ∑

cos(kω0t + Θk ) =

k =1

(1.3)

∞

+ ∑(ak cos kω0t −bk sin kω0t) ,

k =1

где

–

постоянная

составляющая функции x(t) ;

cos( kω0t + Θk )

– k -я

гармоническая составляющая;

, kω0 , Θk – амплитуда, частота и начальная фаза k-й гармони-

ческой составляющей;

ω 0

2 π

– частота основной гармоники

(T – период колебаний).

Ряд Фурье (1.3) с учетом свойств периодической функции x(t)

приобретает еще более простой вид:

∞

x(t) = ∑bk

sin kω0t

– нечетная функция;

k =1

∞

x(t) =

∑ak

cos kω0t

– четная функция.

k =1

Коэффициенты ak и bk

вычисляются в соответствии с выраже-

ниями

T / 2

cos Θk

∫x(t)cos(kω0t)dt,

T −T / 2

T / 2

sin Θk

∫x(t)sin(kω0t)dt

−T / 2

и связаны между собой формулой

a k2 + bk2 .

Комплексная форма ряда Фурье имеет вид

∞

x (t ) =

∑ Ak e jk ω0 t

(1.4)

2 k = −∞

где A

e jΘk

– комплексная амплитуда гармонической со-

ставляющей частоты kω0 , вычисляемая по формуле

T / 2

− jkω t

∫x(t)e

dt =

−T / 2

/ 2

∫x(t)cos(kω0t)dt − j

∫x(t)sin(kω0t)dt = ak − jbk

;

−T / 2

Θk = −arctg

– начальная фаза.

Совокупность модулей амплитуд и соответствующих частот гармоник называют спектром амплитуд – Ak (ω) , совокупность начальных фаз и соответствующих частот гармоник – спектром

фаз Θk (ω).

Спектр амплитуд и спектр фаз однозначно определяют сигнал. На рис. 1.1 даны графические изображения спектра амплитуд и спектра фаз периодического сигнала. Характерной особенностью спектров периодического сигнала является его дискретность.

Ak (ω)

Θk (ω)

Θ3

Θ1

Θ5

ω ω

0 ω0 2 ω0 3ω0 4 ω0 5 ω0

Рис. 1.1. Спектральные характеристики периодического сигнала

Дискретный спектр не обязательно означает периодичность функции x(t) . Последнее имеет место лишь в случае, когда рас-

стояние между спектральными линиями кратны основной частоте ω0 . При невыполнении этого условия спектр описывает так назы-

ваемую почти периодическую функцию. Примером такой функции может служить спектр амплитудно-модулированного сигнала с гармонической модулирующей функцией, частота которой несоизмерима с частотой несущей.

При рассмотрении спектров основных видов сигналов главное внимание уделяется определению их ширины, поскольку в основном этот фактор используется для согласования сигнала с аппаратурой обработки информации (каналом): для исключения потери

информации ширина спектра не должна превышать полосы пропускания канала. Ширина спектра, как правило, определяется через его энергетическую характеристику – среднюю мощность. Средняя мощность периодического колебания и распределение этой мощности между отдельными гармониками имеет вид

		A	2	1	∞		2

x 2					∑
	(t) =	0	+			Ak	.

		2		2 k =1

Пример. Найти спектр последовательности прямоугольных импульсов (рис. 1.2)

			T
+h, iT		≤t <		+iT ;
+h, iT		≤t <	2	+iT ;
x(t) =	T		2
x(t) =
−h, −		+iT ≤t <iT, i =0,±1,±2,...,
−h, −		+iT ≤t <iT, i =0,±1,±2,...,
	2
	2

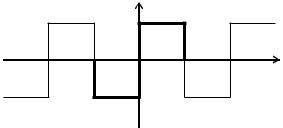
называемой меандром.

x(t)

-T/2 T/2

Рис. 1.2. Меандр

Поскольку функция x(t) нечетная, разложение будем искать в

виде ( ak = 0)

∞

x(t) = ∑bk sin kω0t .

k =1

Спектр амплитуд вычисляется следующим образом:

T / 2

∫

x(t) sin( kω0t)dt =

∫sin( kω0t)dt =

−T / 2

= −

cos kω0t

T / 2

= −

(cos kπ −1) =

kω0

kπ

, k =

1,3,5,...;

kπ

0, k = 2,4,6,... .

Спектр фаз имеет вид	bk		π .
Θk = −arctg		= −
	0
			2

Спектральные характеристики меандра приведены на рис. 1.3. Окончательно тригонометрический ряд Фурье будет иметь вид:

x(t) =

(sin ω0t +

sin 3ω0t +

sin 5ω0t +...) .

Ak (ω)

ω0 3ω0 5ω0 7ω0 ω

Θk (ω)

4h/ π

4h/3 π

- π/2

4h/5 π

4h/7 π

ω0 3ω0 5ω0 7ω0

Рис. 1.3. Спектр амплитуд и спектр фаз меандра

Модель одного периода сигнала задана с тремя разрывами первого рода (скачками). Любой скачок функции содержит все частоты диапазона до бесконечности, в связи с чем ряд Фурье также бесконечен и очень медленно затухает. Однако одним из важных достоинств преобразования Фурье является то, что при ограничении (усечении) ряда Фурье до любого конечного числа его членов

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете Интегрированные системы управления и проектирования