В.М. Волков Математика и математика в экономике. Программа, контрольные работы №4, 5, 6 и методические указания для студентов 2 курса заочной формы обучения

10

Пример.

∫x arctgxdx = ∫arctgx xdx , то есть возьмём

dx

u = arctgx du =

,

1 + x

2

2

x

dv = xdx v = ∫dv = ∫xdx =

.

2

(здесь при нахождении v константу c полагаем равной 0). Получим

∫x arctgxdx = ∫arctgx xdx =

x2

arctgx −

1

∫x2

dx

.

2

2

1 + x2

dx

Возьмём

∫x2

отдельно

+ x2

1

∫x2

dx

x2 + 1 −

1

1 −

1

dx

= x − arctgx + c .

=

∫

dx =

∫

dx

= ∫dx

− ∫

+ x2

x2 + 1

1 + x2

1 + x2

1

Итак

∫x arctgxdx = x2 arctgx − 1 (x − arctgx)+ c .

2

2

Пример. Найти

∫x e−3xdx . Пусть

u = x du = dx,

−3x

−3x

1

−3x

1

d(− 3x)= −

−3x .

dv = e

dx v =

∫e

dx

= −

∫e

e

3

3

∫x e

−3x

1

e

−3x

1

e

−3x

xe−3x

1

∫e

−3x

dx =

dx = x −

3

− ∫ −

3

dx = −

3

+

3

= − xe−3x

− e−3x + c .

3

9

Пример. При вычислении интеграла I = ∫ 2 +

x + 1 dx

сделаем под-

x + 3

становку u =

x + 1 u2 = x + 1 x = u2 − 1 dx = 2udu,

x + 3 = u2 − 1 + 3 = u2 + 2 . Получим

2u + u2 du .

I = ∫

2 +

x + 1 dx = ∫

2 + u 2udu = 2∫

2u + u2

x + 3

u2 + 2

u2 + 2

Дробь

неправильная (степень числителя не меньше степени

u2 + 2

знаменателя). Выделим целую часть

11

(u2 + 2)− 2 + 2u

= 1 −

2

+

2u

.

2u + u2

u2 + 2

u2 + 2 u2 + 2

Итак

I =

2∫

du =

−

∫

2du

+

2udu

4

arctg

u

+

u2 + 2

2 ∫du

u2

∫

= 2u −

2

2

+

2

u2

+ 2

+ 2 ln(u2 + 2)+ c = 2 x +1 − 4

arctg

x +1 + 2 ln x + 3 + c .

du

2

2

Здесь ∫du и ∫

табличные, а

u2 +

2

+ 2)

2

2udu

∫

=

∫

d(u

= ln(u2 + 2)+ c .

2

2

+ 2

u + 2

u

В пункте в приведены интегралы от дробнорациональных функций, метод интегрирования которых приведён в литературе [1, гл. YII,

с. 303-311; 7, гл. IX, с. 235-245].

Пример. Найти ∫			x2 −		2	dx.
	x	3	− 4x	2	+ 3x

Подынтегральная функция является правильной дробно - рациональной функцией, так как степень числителя меньше степени знаменателя. Для разложения её в сумму простейших дробей найдём корни знаменателя x3 − 4x2 + 3x = x(x2 − 4x + 3)= 0. Тогда x = 0,x =1,x = 3 . Так как корни действительные и различные числа, разложение имеет

вид	x2 − 2	=	A	+		B		+	C		. Для нахождения неопределённых ко-
	x3 − 4x2 + 3x		x			x −	1		x −	3
эффициентов A,B,C					приводим к общему знаменателю выражение в

правой части и приравниваем числители

x2 − 2 = A(x −1)(x − 3)+ Bx(x − 3)+ Cx(x −1).

Подставляя в это равенство корень x = 0, получаем − 2 = 3A A = − 23 .

При x =1, получаем −1 = −2B B =	1	. При x = 3 , получаем
	2

7 = 6C C = 76 . Заменяя подынтегральное выражение, получаем

12

−

2

1

7

x

2

−

2

dx

dx

3

2

6

∫

dx = ∫

+

+

dx = − 2 ∫dx + 1 ∫

+ 7 ∫

=

3

2

x

x −1

x −

3

x

− 4x

+ 3x

3

3 x 2 x −1 6 x −

= −

2

∫

dx

+

1

∫

d(x −1)

+

7

∫d(x − 3)

= −

2 ln x +

1 ln x −1 +

7 ln x − 3 + C =

3 x 2 x −1

6 x − 3

3

2

6

= ln

x −1 6 (x − 3)7

+ C.

3 x2

Для нахождения площадей плоских фигур и объёмов тел вращения в задачах № 31-60 рекомендуется изучить литературу [1, гл.8, с. 340-344, 347; 3, гл.6, с. 340-346; 4, гл.12, с. 416-418,426; 6, гл.5, с. 189,199; 7, гл.10, с. 269-271].

При вычислении интегралов в этих задачах и в дальнейшем можно пользоваться таблицей интегралов в справочниках [10, с. 841-851; 11,

с. 114-156].

Пример. Найти площади частей, на которые круг x2 + y2 = 12 делится параболой y = x2 .

Сделаем схематический чертёж ( рис.5) и найдём точки пересечения этих линий

							2	+ y		2	= 12						2	= 12 − y			2
					x										x							12	− y2 = y
									2								2
																		= y
					y = x										x
					y2 + y − 12 = 0 y = − 1 ± 1 + 48 = − 1 ± 7 , y = 3.
																				2			2
		В	точке			пересечения								x2 = 3 x1 = −								3, x2 =			.		Площадь							меньшей
																								3
части
			3								3				x								x					3			x3			3
S1 =			∫	12 − x2 dx −							∫ x2dx =							12 − x2 + 6 arcsin												−				=
																2							12								3
		−	3								− 3																−		3				−	3
=		3	12 − 3 + 6 arcsin									3	−			−		3	12	− 3		− 6 arcsin				3			−
		2										12					2								12
−		3	3	−	− 3		3							π		− 2 3 = 3 + 2π.
		3			3			= 3 3 + 12						6

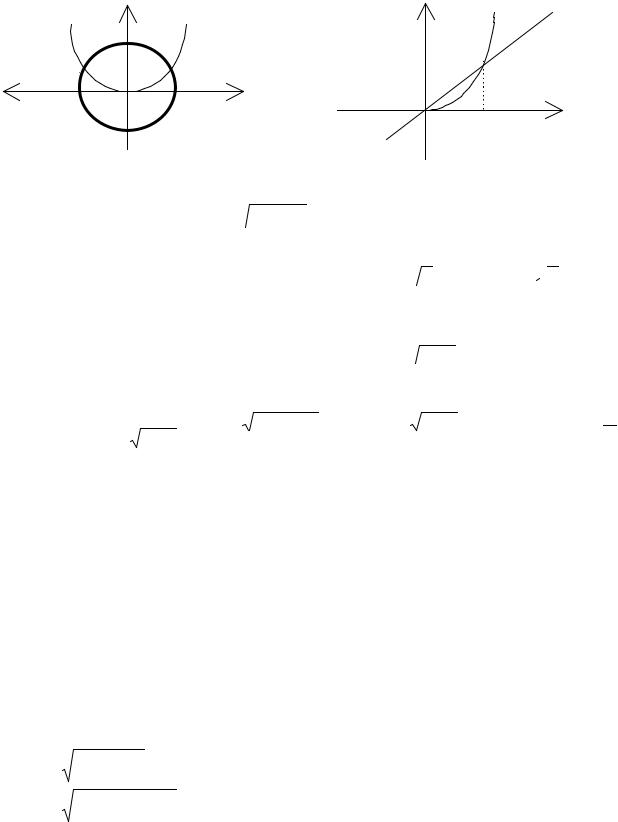
				13
	y	y = x2		y
				y = x
			x	x
	x2	+ y2	=12
	Рис.5			Рис.6

При вычислении интеграла ∫ 12 − x2 dx мы воспользовались справочником [10] (интеграл № 51) или [11] (интеграл № 157).

Площадь большей части S2 = πr2 −S1 = π 12 − 3 − 2π = 10π − 3 .

Пример. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями y = x, y = x sinx, 0 ≤ x ≤ π .

Сделаем схематический чертёж ( рис.6) и найдём точки пересечения

этих линий y = x	x − x sinx =
y = x	sinx
	π

0, x1 = 0, 1 − sinx = 0, sinx = 1, x2 = π2 .

π

			b	b
V = V1 − V2 = π∫y12dx − π∫y22dx = π∫2 x2dx − π∫2 x2 sin xdx =
			a	a			0			0
		3				π			3
	x					2		π
= π			− 2xsin x + (x2	− 2)cosx			= π			− π + 2	,
	3							24
						0
∫x2 sin xdx = 2xsin x −(x2 − 2)cosx.

При нахождении длины дуги в задачах № 61-90 следует помнить, что дифференциал длины дуги выражается различными формулами [1,

гл.8, с. 347-352; 4, гл.12, с. 432-436; 7, гл.10, с.270].

1. ds = 1 + (y′x )2 dx , если линия задана в декартовых координатах;

2. ds = (x′t )2 + (y′t )2 dt , если линия задана параметрически

x = x(t), y = y(t);

14

3. ds = r2 + (r′(θ))2 dθ, если линия задана в полярных координатах

r = r(θ).

Пример. Найти длину дуги кривой r = cos2 θ												,	0 ≤ θ ≤						π .
										θ	2				θ			1	2
Вычисляем ds = r2			+ (r′(θ))			2	dθ, rθ′		= 2cos										.
										2	− sin				2			2
r2 + (r′(θ))	2	= cos4	θ	+ cos2	θ		sin2	θ	= cos2	θ				θ		+ sin2				θ		= cos2	θ	,
			2		2			2		2	cos2			2									2
																				2

ds = cos2 θ2dθ = cos θ2 dθ,

ππ

2	θ	dθ = 2sin	θ		2		π		= 2	2	= 2 .
S = ∫cos						= 2 sin		− sin0
0	2		2		0		4			2

При решении задач № 91-120 необходимо изучить криволинейные интегралы второго рода (по координатам) и научиться их вычислять в зависимости от задания пути интегрирования [2, с. 82-89; 3, с. 472-479; 5, с.217-226].

r	Пример.		r	Вычислить		работу,	совершаемую	силой
				r	при перемещении некоторой массы по дуге
F = (x2		− 2xy)i + (y2 − 2xy)j
параболы y = x2				от точки A(1,1) до точки B(-1,1).
	Составляем криволинейный интегралA =						∫ (x2 − 2xy)dx + (y2 − 2xy)dy .
Так как y = x2 , то y′ = 2x,							AB
					dy = 2xdx , и при движении массы из точки A

в точку B x принимает значения от 1 до -1, которые и будут пределами интегрирования по одной переменной x . Следовательно, имеем

A =		∫ (x	2	− 2xy)dx + (y	2	− 2xy)dy			=		1					2	− 2x				3						2	)	2	− 2x			x	2
											∫		(x									)+ (x														2x dx =
		AB									−1
	1						x	3				2x		4				2x	6				4x	5			1				14
=	∫	(x2 − 2x3 + 2x5 − 4x			4 )dx =					−					+						−								=			.
							3										6						5								15
	−1												4														−1

15

r	Пример.	Вычислить работу,	совершаемую		переменной	силой
	r	r
F = −y2x i + x2y j при перемещении некоторой массы по дуге кривой,
заданной параметрически x = cost,			y =	sin t , от точки A до точки B с
соответствующими значениями параметра t1 = 0, t2					= π .
					2
	Составляем криволинейный интеграл			A = ∫ (− xy2 )dx + x2ydy		и сво-
				AB

дим его к определённому интегралу по t . Для этого находим дифференциалы

dx = d(	cost)=	− sin t	sin t)=	cost
		2 cost dt, dy = d(		2 sin t dt .

После подстановки вместо x, y,dx,dy их выражений через t криволи-

нейный интеграл превращается в определённый интеграл по переменной t , то есть

π

(− sin t)

2

cost

+ cost

sin t

cost

A = ∫

− sin t

2 cost

dt =

0

2 sin t

π

π

π

2

=

1

2

1

2

1

dt =

1

t

π

.

2

∫(sin2 t + cos2 t)dt =

2

∫

2

=

4

0

0

0

r

r

Пример.

Вычислить

работу,

совершаемую силой

− 3xy j

F = x2

i

при перемещении некоторой массы из точки A(1,2) в точку B(4,0) по прямой линии.

Напишем уравнение прямой AB, используя уравнение прямой, про-

ходящей через две данные точки																	y − y1								=	x − x1						. Получим
																y2 − y1										x2 − x1
y − 2	= x − 1,			y − 2 = x − 1, y = −												2			(x − 1)+ 2, y = −														2 x + 8							, dy = −			2 dx .
0 − 2 4 − 1				− 2					3							3																	3						3				3
Искомая работа равна													4													2				8					2
						2											2
			A = ∫x				dx	−	3xydy = ∫ x										− 3x −								x +				−						dx				=
																										3
				AB									1																	3					3
4		x3		16x						1		x3		16						x2				4				1	(64 −				1)+				8		(16			− 1)= 33 .
= ∫	−		+		dx =				−				+												= −
		3		3						3		3		3						2								9									3
1																								1

16

Контрольная работа №6

Данная контрольная работа включает в себя задачи по теме «Дифференциальные уравнения».

В задачах № 1-30 при отыскании общего решения дифференциального уравнения первого порядка следует использовать литературу [1,

с.105-107, 110-111, 118-120; 2, с. 22-27, 30-34; 3, с. 198-203; 4, с. 568575; 5, с. 389-394].

Перед решением задач нужно определить тип уравнения и метод решения, при этом можно руководствоваться табл.1.

Таблица 1 Классификация дифференциальных уравнений первого порядка

Тип

дифферен-

Вид уравнения

Метод решения

циального

урав-

нения

первого

порядка

1. С

разделяю-

dy

= f1(x) f2 (y)

∫

dy

= ∫f1(x)dx

dx

f2 (y)

щимися

пере-

менными

2. Однородное

dy

= f

Подстановка

y

= u, y = ux ,

y

dx

x

x

y′ = u′x + u

приводит к

уравнению первого типа

3. Линейное

dy

+ P(x)y = Q(x)

Подстановка y = u(x) v(x)

dx

приводит к уравнениям

первого типа

dy

+ P(x) v = 0,

dx

du

v = Q(x)

dx

Пример. Найти общее решение уравнения siny′x = y .

Так как y′ = dydx , то получаем уравнение dydx = y sinx - уравнение пер-

вого типа. Разделяем переменные :

dyy = sinx dx, ∫ dyy = ∫sinxdx, ln y = −cosx + c,

17

где c - произвольная постоянная. Можно оставить решение в таком виде или выразить y в явном виде

y = e− cos x+c .

y

Пример. Найти общее решение уравнения y′ = ex + xy .

Это уравнение второго типа, однородное, следовательно, делаем

подстановку

y

= u, y = ux, y′ = u′x + u . Уравнение примет вид

x

du x = eu ,

du

= eu .

u′x + u = eu + u,

dx

dx

x

Получили уравнение с разделяющимися переменными:

du

=

dx

,

∫

du

=

∫

dx

, − e−u

= ln

x

+ lnc .

eu

x

eu

x

Здесь мы обозначили произвольную постоянную не c , а lnc для удобства записи:

− e−u = ln				, u = y	− e−	y	= ln		cx		.
		cx				x
				x
Можно оставить решение в таком виде, а можно y выразить явно:

e−

y

= −ln

cx

, e−

y

= ln

1

, − y

= lnln

1

, y = −xlnln

1

.

x

x

cx

x

cx

cx

Пример. Найти общее решение уравнения y′ + 2y = x .

Это линейное уравнение P(x)= 2,

Q(x)= x (табл.1). Делаем подста-

новку y = u(x) v(x), y′ = u′v + uv′. Подставив эти соотношения в исход-

ное уравнение, получаем u′v + uv′ + 2uv = x . Одну из функций находим из уравнения

		uv′ + 2uv = 0,	dv + 2v = 0 ,
			dx
тогда вторая функция u определяется из уравнения u′v = x .
Решая первое уравнение, находим функцию v , то есть
dv = −2v,	dv	= −2dx, ∫ dv = −∫ 2dx, ln			v		= −2x,	v = e−2x	,
dx	v	v

произвольную постоянную для v полагаем равной нулю. Получаем уравнение для нахождения функции u:

18

du

e

−2x

= x,

du =

x

dx, du = x e

2x

dx, ∫du = ∫x e

2x

dx,

dx

e−2x

u =

1 x e2x −

1

∫e2xdx =

1 x e2x −

1 e2x

+ c .

2

2

2

4

Решение исходного уравнения имеет вид

y = uv = 12 xe2x − 41 e2x + c e−2x .

В задачах № 31-60 для решения дифференциальных уравнений второго порядка следует изучить литературу [1, с. 126-131; 2, с. 58-63; 3,

с. 210-212; 4, с. 582-585; 5, с. 397-400].

Уравнения второго порядка допускают понижение порядка ( то есть сводятся к уравнениям первого порядка) в двух случаях (табл.2).

Таблица 2 Дифференциальные уравнения второго порядка, допускающие пони-

жение порядка

Вид уравнения	Подстановка,	применяемая
	для понижения порядка
1. y′′ = f (x, y′) - уравнение в явном виде не	y′ = u(x), y′′ =	du .
содержит функцию y .		dx
2. y′′ = f (y, y′) - уравнение в явном виде не	y′ = u(y), y′′ = u du .
содержит переменную x .		dy

Пример. Найти общее решение уравнения 1 + y′ = y′′ x.

Это уравнение не содержит в явном виде функциюy , делаем под-

становку y′ = u(x),

y′′ =

du . Уравнение примет вид

dx

du

du

1

1 + u = dx x

dx

= (1 + u)x .

Разделим переменные:

du

= dx ,

∫

du

= ∫ dx, ln

1 + u

= ln

x

+ lnc1 , ln

1 + u

= ln

c1x

,

1 + u

x

1 + u

x

1 + u = c1x, u = c1x − 1.

Так как u = dy , получаем dy = c1x − 1,

dy = (c1x − 1)dx .

dx

dx

19

Интегрируя это равенство, получим общее решение исходного уравнения

y = c1 x2 2 − x + c2 .

Пример. Найти общее решение уравнения y′′ y2 = (y′)3 .

Это уравнение не содержит в явном виде переменную x , применяем

подстановку y′ = u(y),

y′′ = u

du .

dy

Уравнение примет вид

= u3 ,

= u2 .

u du

y2

= u

3 , u du

du

dy

dy

y2

dy

y2

Это уравнение с разделяющимися переменными:

du

=

dy

,

∫

du

=

∫

dy

, −

1

= −

1

+ c1 .

u

y

u2

y2

u2

y2

Отсюда находим, что u =

y

, так как u = dy

, то dy

=

y

.

1

− c1y

1 − c1y

dx

dx

Разделяя переменные, получим

1 − c

y

1

− c1y = x + c2 .

1

dy = dx,

∫

− c1

dy = ∫dx,

ln

y

y

y

Это общий интеграл уравнения, y выразить в явном виде отсюда невозможно.

В задачах № 61-90 использую приёмы решения дифференциальных уравнений второго порядка с постоянными коэффициентами, изложен-

ные в литературе [1, с. 135-144; 2, с. 77-82, 84-94; 3, с. 224-233; 4, с. 597-607; 5, с. 400-410].

Для нахождения общего решения однородного дифференциального уравнения используют табл. 3, а для нахождения частного решения неоднородного дифференциального уравнения - табл. 4.