В.М. Волков Математика. Программа, контрольные работы №7, 8 и методические указания для студентов-заочников инженерно-технических специальностей 2 курса

10

Составляем криволинейный интеграл A = ∫ (− xy2 )dx + x2ydy и

AB

сводим его к определённому интегралу по t . Для этого находим дифференциалы

dx = d(	cost)=	− sin t	sin t)=	cost
		2 cost dt, dy = d(		2 sin t dt .
После подстановки вместо x, y,dx,dy			их выражений через t

криволинейный интеграл превращается в определённый интеграл по переменной t , то есть

π

(− sin t)

2

− sin t

cos t

+ cost

sin t

cost

A = ∫

2

cost

2

dt =

0

sin t

π

π

π

2

=

1

2

(sin2 t + cos2 t)dt =

1

2

1

dt =

1

t

=

π

.

2

∫

2

∫

2

4

0

0

0

r

r

Пример. Вычислить

работу, совершаемую

силой

− 3xy j

F = x2

i

при перемещении некоторой массы из точки A(1,2) в точку B(4,0) по прямой линии.

Напишем уравнение прямой AB, используя уравнение прямой,

проходящей через две данные точки																								y − y1								=			x − x1				. Получим
																								y2 − y1
																																		x2 − x1
y − 2 = x − 1,					y − 2 = x − 1, y = −											2			(x − 1)+ 2, y = − 2 x + 8 , dy = −																										2 dx .
0 − 2 4 − 1						− 2				3						3																					3	3							3
Искомая работа равна															4															2					8			2
								2												2
				A = ∫x					dx	−	3xydy = ∫ x											− 3x −										x +					−				dx =
																														3
						AB									1																					3		3
4			x3			16x						1		x3			16						x2					4					1	(64 − 1)+							8		(16	− 1)= 33 .
= ∫		−		+			dx =				−				+														= −
			3		3							3		3					3														9								3
1																							2					1

В задачах № 121-150 нужно построить заданную область интегрирования D и вычислить двойной интеграл в декартовых координатах или в полярных координатах. Теоретический материал по этой теме изложен в литературе интегрирования [2, гл.10, с. 53-63; 3, гл.8, с.437450; 9, гл.1, с.5-10].

11
Пример. Вычислить ∫∫(3x + y2 )dxdy,			≥	1
		D = y		x	; y ≤ 2x; x ≤ 3 .
D	1
Построим границы области y =		; y = 2x; x = 3				(рис.3). Найдём
	x

координаты точек их пересечения A,B,C.

Для A:

Для B:

Для C:

							1 , 2x −						1			= 0,	2x	2	− 1	= 0, 2x2 = 1,
y = 2x, 2x =
							x						x					x
	1			, x2	=	1			, x =			1			, y =		2		=	1
y =																				2, A		, 2 .
		x				2							2				2				2
y = 2x,					y = 6, B(3,6).
	3,
x =
	1			,
y =							1							1
		x			y =					,	C	3,				.
							3
	3,													3
x =

B

y

y = 2 x

y

y = 2x

A

A

1

x + y = 3

C

y =

x

O

B

3

0

x

x

		Рис.3									Рис.4
	В данной области D				x, y удовлетворяют условиям
1	≤ x ≤ 3,	1		≤ y ≤ 2x .
2			x
				∫∫(3x + y2 )dxdy =		3	2x			(3x	+ y2 )dy .
	Находим
						∫dx ∫
				D		1		1
						2		x

Вычислим внутренний интеграл, в котором считаем x постоянным, подставим вместо y его пределы интегрирования, затем вычислим

внешний интеграл

3			y3				2x		3					1		1		3		1
∫	3xy	+	3					dx =	∫		3x	2x	−		+		8x		−		dx =
1							1		1					x		3				x3
2									2

x

12

	3					2			8			3		1						x3				8		x4			1		x−2					3
=	∫			6x			−	3 +	3	x			−		dx		=		6	3		− 3x +		3		4		−	3							=
	1													3x3																	(− 2)						1
	2						1							1		2						1			1		1									2
	33										3							34											− (		2)	2				= 100 .
= 2			−		(		2)	3 − 3					−		+					−	( 2)		4	+				2
														2		3									6 3

Иногда удобней внешний интеграл вычислять по переменной y , а внутренний по x .

Пример. Вычислить ∫∫ ydxdy, D = {y ≤ 2 x; x + y ≤ 3; y ≥ o}.

D

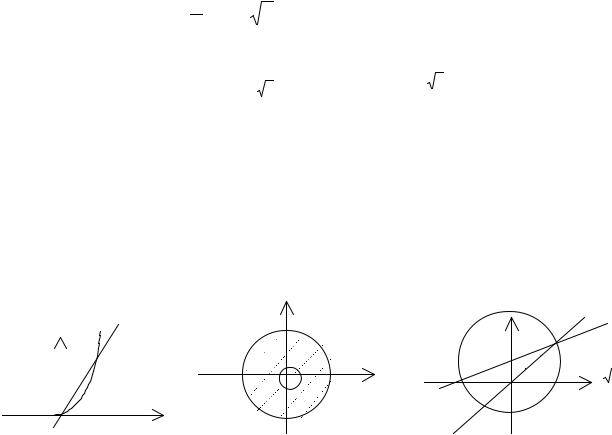
Построим область D (рис.4). Координаты точек пересечения O(0,0); A(1,2); B(3,0). В области D y удовлетворяет условию 0 ≤ y ≤ 2. При это

область D слева ограничена кривой y = 2x , справа линией x + y − 3 = 0.

Для определения границ изменения выразим из этих уравнений x как функцию от y , то есть

					x = y2	, x = 3 − y.
			4				y2
Следовательно, в области D справедливо								≤ x ≤ 3 − y.
		2	3−y				4
Находим
	∫∫ ydxdy = ∫dy ∫ ydx .
	D	0		y 2
			4

При вычислении внутреннего интеграла считаем y постоянным

2			3−y		2					y2		2						−	y3
∫ yx			y 2		dy = ∫	y(3	− y)− y			2	dy	= ∫			3y − y2				4	dy =
0					0							0
	4
														2
							y2		y3		y4					1	.
						= 3		−		−					= 2
							2		3		4 4					3
														0

13

В некоторых задачах решение равноценно при любом порядке интегрирования, но следует помнить, что пределами внешнего интеграла всегда являются числа, а пределами внутреннего интегралауравнения линий.

	x2
Пример. Вычислить	∫∫D y2 dxdy, D = {y ≥ x2; y ≤ 2x}.

Построим область D (рис.5). Координаты точек пересечения O(0,0);

										0 ≤ y ≤ 4,
A(2,4). В области D										y		≤ x ≤			y.
											2
Находим
						x2						4			y x2								4			x3							y
																								1
					∫∫				dxdy = ∫dy ∫												dx = ∫													dy =
																	y2											3
					D y2							0			y								0	y2							y
				3											2			1													2		1									1
								3																															2
4	1		y 2				y					4		1		−		2				1							2				2		1			y					= 1.
= ∫					−					dy = ∫					y					−			y dy =							y				−
		2												3								24							3						24			2
0 y			3				8 3					0
																																										0

Если область D - круг или часть круга, удобнее вычислить двойной интеграл, переходя к полярным координатам.

y

x2

+ y 2 = 9

y

y = x

y

y = 2x

y =

1

A

O

x

1

3

x

y = x2

x

O

x

Рис.6

Рис.7

Рис.5

Пример. Вычислить

∫∫e−x 2 −y 2 dxdy,

D = {1 ≤ x2 + y2 ≤ 9}.

D

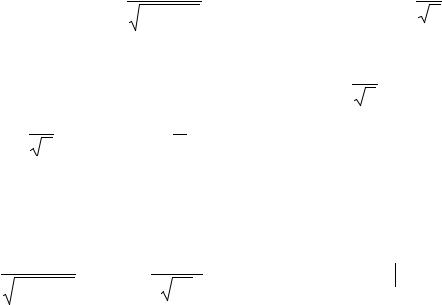
Построим границы области точке O(0,0) и радиусом R=1,

x2 + y2 = 1 x2 + y2 = 9

-окружность с центром в

-окружность с центром в

точке O(0,0) и радиусом R=3 (рис.6).

Полагая x = r cosϕ,	x2 + y2 = r2 , dxdy = rdrdϕ, имеем
y = r sinϕ,

14

∫∫e−x 2 −y 2 dxdy = ∫∫e−r 2

rdrdϕ.

D

D

В области D :

0 ≤ ϕ ≤ 2π,

1 ≤ r ≤ 3. Находим

−x

2 −y

2

−r 2

2π

3

−r 2

2π

3

1

−r 2

2

)

∫∫e

dxdy = ∫∫e

rdrdϕ = ∫dϕ∫e

rdr = −

∫dϕ∫

e

d − r

=

2

D

3

D

0

1

0

1

(

1

2π

−r 2

1

(e

−9

−1

)ϕ

2π

1

(e

−9

−1

)2π

1

1

= −

∫

e

dϕ = −

− r

= −

− r

=

−

π .

2

0

1

2

1

0

2

e

e9

Пример. Вычислить

∫∫

dxdy,

+ y2

≤ R

2 ,

x

x

D = x2

3

≤ y ≤ x .

D

2 + y2

Построим область D (рис.7). В области D :

0 ≤ r ≤ R .

Пределы

изменения ϕ определим из уравнений прямых y =

x

,

y = x .

1

π

3

Так k1 = tgϕ1 ,

= tgϕ1

,

ϕ1 =

,

3

π

6

π

π .

k2 = tgϕ2 ,

1 = tgϕ2 ,

ϕ2 =

, то есть

≤ ϕ ≤

Находим

4

6

4

π

π

	1	dxdy = ∫∫ rdrdϕ =								R
∫∫					∫∫drdϕ = 4∫dϕ∫dr
D x2 + y2		D		r2	D				π 0
									6
			π	π		π			1
			π4							πR .
		= R ϕ		= R	−			=
		6		4		6			12

=4∫r R0 dϕ =

π

6

Контрольная работа №8

Данная контрольная работа включает в себя задачи по теме «Дифференциальные уравнения».

В задачах № 1-30 при отыскании общего решения дифференциального уравнения первого порядка следует использовать литературу [1,

с.105-107, 110-111, 118-120; 2, с. 22-27, 30-34; 3, с. 198-203; 4, с. 568575; 5, с. 389-394].

Перед решением задач нужно определить тип уравнения и метод решения, при этом можно руководствоваться табл.1.

15

Пример. Найти общее решение уравнения siny′x = y .

Так как y′ = dydx , то получаем уравнение dydx = y sinx - уравнение

первого типа. Разделяем переменные

dyy = sinx dx, ∫ dyy = ∫sinxdx, ln y = −cosx + c,

где c - произвольная постоянная. Можно оставить решение в таком виде или выразить y в явном виде

y = e− cos x+c .

y

Пример. Найти общее решение уравнения y′ = ex + xy .

Это уравнение второго типа, однородное, следовательно, делаем подстановку xy = u, y = ux, y′ = u′x + u . Уравнение примет вид

Таблица 1

Дифференциальные уравнения первого порядка

Тип

дифференци-

Вид уравнения

Метод решения

ального уравнения

первого порядка

1. С

разделяющи-

dy

= f1(x) f2 (y).

∫

dy

=

∫f1(x)dx .

dx

f2 (y)

мися

переменны-

ми.

2. Однородное.

dy

y

Подстановка

y

= u, y = ux ,

dx

= f .

x

x

y′ = u′x + u

приводит к

уравнению первого типа.

3. Линейное.

dy

+ P(x)y = Q(x).

Подстановка y = u(x) v(x)

dx

приводит

к

уравнениям

первого

типа

dy

+ P(x) v = 0,

dx

du

v = Q x

.

dx

(

)

	16
u′x + u = eu + u,	du	x = eu ,	du	= eu .
	dx		dx	x

Получили уравнение с разделяющимися переменными

du

=

dx

,

∫

du

= ∫

dx

, − e−u = ln

x

+ lnc .

eu

x

eu

x

Здесь мы обозначили произвольную постоянную не c , а lnc для удобства записи

− e−u = ln				, u = y	− e−	y	= ln		cx		.
		cx				x
				x
Можно оставить решение в таком виде, а можно y выразить явно

e−

y

= −ln

cx

, e−

y

= ln

1

, − y = lnln

1

, y = −xlnln

1

.

x

x

cx

x

cx

cx

Пример. Найти общее решение уравнения y′ + 2y = x .

Это линейное уравнение

P(x)= 2,

Q(x)= x (табл.1). Делаем

подстановку y = u(x) v(x), y′ = u′v + uv′. Подставив эти соотношения в

исходное уравнение,		получаем	u′v + uv′ + 2uv = x . Одну из						функций
находим из уравнения				dv + 2v = 0 ,
		uv′ + 2uv = 0,
				dx
тогда вторая функция u определяется из уравнения u′v = x .
Решая первое уравнение, находим функцию v , то есть
dv = −2v,	dv	= −2dx, ∫ dv	= −∫ 2dx, ln			v		= −2x, v = e−2x	,
dx	v	v

произвольную постоянную для v полагаем равной нулю. Получаем уравнение для нахождения функции u

du

e

−2x

= x,

du =

x

dx, du = x e

2x

dx, ∫du = ∫x e

2x

dx,

dx

e−2x

u =

1 x e2x −

1

∫e2xdx =

1 x e2x −

1 e2x

+ c .

2

2

2

4

Решение исходного уравнения имеет вид

y = uv = 12 xe2x − 41 e2x + c e−2x .

17

В задачах № 31-60 для решения дифференциальных уравнений второго порядка следует изучить литературу [1, с. 126-131; 2, с. 58-63; 3, с. 210-212; 4, с. 582-585; 5, с. 397-400].

Уравнения второго порядка допускают понижение порядка ( то есть сводятся к уравнениям первого порядка) в двух случаях (табл.2).

Таблица 2 Дифференциальные уравнения второго порядка, допускающие

понижение порядка

Вид уравнения	Подстановка,	применяемая
	для понижения порядка
1. y′′ = f (x, y′) - уравнение в явном виде не	y′ = u(x), y′′ =	du .
содержит функцию y .		dx
2. y′′ = f (y, y′) - уравнение в явном виде не	y′ = u(y), y′′ = u du .
содержит переменную x .		dy

Пример. Найти общее решение уравнения 1 + y′ = y′′ x.

Это уравнение не содержит в явном виде функциюy , делаем

подстановку y′ = u(x),

y′′

= du

. Уравнение примет вид

dx

du

du

1

1 + u = dx

x

dx

= (1 + u)x .

Разделим переменные

du

= dx ,

∫

du

= ∫ dx, ln

1 + u

= ln

x

+ lnc1 , ln

1 + u

= ln

c1x

,

1 + u

x

1 + u

x

1 + u = c1x, u = c1x − 1.

Так как u = dy , получаем

dy = c1x − 1,

dy = (c1x − 1)dx .

dx

dx

Интегрируя это равенство, получим общее решение исходного уравнения

y = c1 x2 2 − x + c2 .

Пример. Найти общее решение уравнения y′′ y2 = (y′)3 .

18

Это уравнение не содержит в явном виде переменную x , применяем

подстановку y′ = u(y),

y′′ = u

du .

dy

Уравнение примет вид

= u3 ,

= u2 .

u du

y2

= u

3 , u du

du

dy

dy

y2

dy

y2

Это уравнение с разделяющимися переменными

du

=

dy

,

∫

du

=

∫

dy

, −

1

= −

1

+ c1 .

u

y

u2

y2

u2

y2

Отсюда находим, что u =

y

, так как u = dy

, то dy

=

y

.

1

− c1y

1 − c1y

dx

dx

Разделяя переменные, получим

1 − c

y

1

− c1y = x + c2 .

1

dy = dx,

∫

− c1

dy = ∫dx,

ln

y

y

y

Это общий интеграл уравнения, y выразить в явном виде отсюда невозможно.

В задачах № 61-90 используются приёмы решения дифференциальных уравнений второго порядка с постоянными коэффициентами,

изложенные в литературе [1, с. 135-144; 2, с. 77-82, 84-94; 3, с. 224-233; 4, с. 597-607; 5, с. 400-410].

Для нахождения общего решения однородного дифференциального уравнения используется табл. 3, а для нахождения частного решения неоднородного дифференциального уравнения используется табл. 4.

					Таблица 3
		Общее решение однородного уравнения
Вид общего решения однородного			Корни		характеристического
уравнения			уравнения
1.	y0	= c1ek1x + c2ek 2x .	k1 ,k2	-вещественные, k1 ≠ k2 .
2.	y0	= (c1 + c2x)ekx .	k1 ,k2	-вещественные, k1 = k2 .
3.	y0	= (c1 cosβx + c2 sinβx)eαx .	k1 ,k2	-комплексные,
			k1 = α + βi, k2 = α − βi .

19

Пример. Найти частное решение дифференциального уравнения

y′′ + 8y′ + 16y = 2xe−4x ,

удовлетворяющее начальным условиям y(0)= 1, y′(0)= 2.

Решение. Общее решение неоднородного уравнения можно

записать в виде y = y0 + Y , где	y0 -		общее решение однородного
уравнения
y′′ + 8y′ + 16y = 0 ,
			Таблица 4
Частное решение неоднородного уравнения
Вид правой части неоднородного		Вид частного решения
дифференциального уравнения
f (x)= eax Pn (x), Pn (x)- многочлен		y = xr eax Qn (x), где
степени n .		0, еслиa неявляетсякорнем
			характерист. уравнения
		1,еслиa равноодномукорню
		r =	характерист. уравнения
			2,еслиоба корняхарактерист.
			уравненияравныa
		Qn (x)- многочлен степени n с не-
		определёнными коэффициентами
f (x)= eax (Pn (x)cosbx + Qm (x)sinbx),		y = xr eax (SN (x)cosbx + ZN (x)sinbx)
Pn (x)- многочлен степени n ,		0, еслиa + bi неявляетсякорнем
Qm (x)- многочлен степени m .			характерист. уравнения
		r =
		1,еслиa + bi равноодномукорню
			характерист. уравнения
		N равно наибольшей из степеней
		n и m .