В.М. Волков Математика. Программа, контрольные работы №9, 10 и методические указания для студентов-заочников инженерно-технических специальностей 2 курса.2003

10

Составляем закон распределения случайной величины X

	X				1					2	3
	P				2/3					2/9	1/9
	Контроль:	3	2			2		1	= 1. Закон составлен правильно.
		∑pi =			+		+
			3			9		9
		i=1

Вычисляем числовые характеристики. Математическое ожидание

M(X)= ∑xi pi = 1 2 + 2 2												+ 3 1 = 13 .
3
i=1			3						9					9				9
Дисперсию определяем по формуле D(X)= M(X2 )− M2 (X). Здесь
M(X2 )= ∑xi pi = 1 2 + 4 2												+ 9 1 = 23 .
3
i=1				3						9					9				9
D(X) =	23				13			2				38	.
	9	−						=				81
						9

Среднее квадратическое отклонение

σ(X)= D(X) = 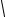3881 ≈ 0,68 .

Внекоторых задачах следует производить непосредственный подсчёт вероятностей возможных значений случайной величины.

Пример. В лотерее из десяти билетов три выигрышных. Наудачу взяты два билета. Составить закон распределения случайной величины X - числа невыигрышных билетов среди отобранных. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение. Случайная величина X - число невыигрышных билетов среди отобранных - может принимать значения: 0, 1, 2. Найдём соответствующие им вероятности.

Событие X = 0 означает, что среди двух взятых билетов оба выигрышных. Тогда

	P(X = 0)=	C32	=	3	=	1	.
		C102		45		15

Событие X = 1 означает, что среди двух взятых билетов один выигрышный и один невыигрышный. Тогда

							11
							P(X = 1)=					C13 C17										=		7		.
														C102								15
Событие X = 2 означает, что среди двух взятых билетов оба невыиг-
рышных. Тогда															C72
								P(X = 2)=											=				7		.
															C102							15
Составляем закон распределения случайной величины X
X		0												1																					2
P		1/15												7/15																					7/15
3	1				7			7
Контроль: ∑pi =				+			+		= 1. Закон составлен правильно.
	15
i=1				15			15
Вычисляем числовые характеристики. Математическое ожидание
M(X)				= ∑xi pi = 0 1 + 1 7																		+ 2 7 = 21 = 1,4 .
				3
				i=1						15							15										15				15
Дисперсию определяем по формуле D(X)= M(X2 )− M2 (X). Здесь
M(X2 )= ∑xi pi = 0 1 + 1 7																							+ 4 7 = 7 ≈ 2,33.
				3
					i=1						15							15										15				3
							D(X)= 2,33 − (1,4)2 = 0,37.
Среднее квадратическое отклонение
					σ(X)= D(X) =											0,37 ≈ 0,61.

Закон распределения непрерывной случайной величины может быть задан функцией распределения F(x) ( интегральная функция) или

функцией плотности вероятностей f (x) (дифференциальная функция).

Для решения задач № 121-150 надо знать определение функции плотности вероятностей, формулы, позволяющие находить числовые характеристики, а также уметь определять вероятность попадания случайной величины в заданный интервал. Соответствующие вопросы из-

ложены в [1, гл.10-11; 2, гл.6, п.1-3].

12

Пример. Функция распределения случайной величины имеет вид

0, x ≤ 0,

F(x)= x , 0 < x ≤ 3,

3

1, x > 3.

Требуется найти плотность распределения, математическое ожидание, дисперсию и вероятность попадания случайной величины в интервал (2,4).

Решение. Найдём функцию плотности вероятностей по определению f (x)= F′(x). Для этого продифференцируем функцию F(x), то есть

0, x ≤ 0,

f (x)= 1 , 0 < x ≤ 3,

3

0, x > 3.

Числовые характеристики вычисляем по формулам

M(X)=	∞	D(X)=	∞	(x − M(X))2 f (x)dx .
	∫x f (x)dx;		∫
	−∞		−∞

Иногда для определения дисперсии удобно использовать формулу

D(X)=	∞	2
	∫ x2 f (x)dx − (M(X)) .

−∞

Так как f (x) задана на разных интервалах различными аналитическими

выражениями, то несобственный интеграл при нахождении математического ожидания и дисперсии будет представлен в виде суммы интегралов

M(X)=	0	3	1	∞		1	3	1		x	2			3		1		9		3	.
	∫x 0	dx + ∫x		dx + ∫x 0	dx =		∫x dx =								=				=
			3			3		3								3
	−∞	0		3			0		2					0			2 2

Дисперсию вычисляем по второй формуле

D(X) =				0							3				1			∞				3	2	1	3	9	=
						∫x2		0 dx + ∫x2							3	dx + ∫x2					0 dx −		=	3	∫x2 dx −	4
				−∞							0							3				2			0		.
	1		x3			3	9		1	9		9	= 3			− 2	1		3	.
=						−		=			−							=
	3		3				4		3			4					4		4
						0

Найдём вероятность попадания случайной величины в заданный интервал по формуле

P(2 < X < 4)= F(4)− F(2)= 1 − 23 = 13 .

13

Для решения задач № 151-180 следует изучить закон нормального распределения. Соответствующий вопрос изложен в [1, гл.12, п.2,5; 2,

гл.6, п.5].

Пример. Случайная величина X распределена по нормальному закону с математическим ожиданием a = 3,2 и средним квадратическим отклонением σ = 0,8 . Записать плотность распределения . Найти вероятность попадания случайной величины в интервал (2,5).

Решение. Так как случайная величина X распределена по нормальному закону, то её функция плотности имеет вид

			−	(x−a)2				−	(x−3,2)2
		1				1
f (x)=					f (x)=			e 2(0,8)2 .
	σ		e 2σ2 ;				2π
		2π			0,8

Вероятность того, что случайная величина примет значение из интервала (2,5), определяется по формуле

β − a

α − a

5

− 3,2

2

− 3,2

P(2

< X < 5)= Φ

− Φ

= Φ

− Φ

=

σ

σ

0,8

0,8

= Φ(2,25)− Φ(− 1,5)

= Φ(2,25)+ Φ(1,5).

	По прил. 2 «Таблица значений функции Φ(x)=	1	x	−	x 2
					2
			∫e
		2π 0

dx » [1, с. 462;

2, 326] определяем значения функции

Φ(2,25)= 0,4878, Φ(1,5)= 0,4332. P(2 < X < 5)= 0,4878 + 0,4332 = 0,921.

Контрольная работа № 10

Для выполнения работы следует изучить соответствующий матери-

ал по литературе [1, гл.15-17; 2, гл.9-13].

Одной из задач математической статистики является установление закономерностей массовых случайных явлений, основанное на изучении результатов наблюдений. Покажем на примере системати-зацию опытных данных и вычисление числовых характеристик.

14

Пример 1. На угольных предприятиях определяли производительность труда рабочих при проходке штрека (случайная величина X ) и скорость проходки (случайная величина Y , м/мес). Результаты наблюдений приведены в табл. 1.

Таблица 1

Исходные данные (выборка)

X	Y	X	Y	X	Y	X	Y	X	Y
0,31	136	0,19	110	0,16	70	0,15	118	0,15	100
0,16	76	0,16	87	0.33	300	0,18	152	0,19	64
0,27	160	0,14	75	0,23	185	0,21	155	0,31	150
0,25	170	0,21	120	0,36	311	0,26	151	0,22	150
0,23	101	0,18	97	0,20	97	0,29	230	0,23	126
0,17	87	0,24	100	0,17	120	0,22	215	0,36	280
0,18	72	0,12	123	0,25	201	0.23	202	0.31	154
0,22	100	0,24	103	0.20	152	0,16	120	0,21	120
0,29	194	0,21	100	0,18	118	0,18	101	0,16	120
0,25	190	0.23	103	0,17	158	0,17	100	0.28	125

По данным X - производительности труда рабочего (табл.1) необходимо:

а) составить вариационный ряд;

б) вычислить выборочную среднюю x , выборочную дисперсию Db , выборочное среднее квадратическое отклонение σx .

Решение. А. Систематизация результатов наблюдения.

Для построения интервального вариационного ряда определим оптимальную величину интервала (шаг) по формуле Стерджеса

h = xmax − xmin ,

1 + 3,2lgn

где xmax , xmin - соответственно максимальные и минимальные значения X, n - объём выборки.

	h =	0,36 − 0,12	=	0,24	≈ 0,04 .
		1 + 3,2lg50		6,44

Величину интервала определяем с той же точностью, с какой заданы исходные данные.

Составим таблицу распределения случайной величины или признака X , называаемую вариационным рядом.

15

Таблица 2 Вариационный ряд производительности труда рабочих

Интервалы J	Частота mi	Частость p*i	Накопленная
			частость F* (x)
[0,12;0,16)	4	0,08	0,08
[0,16;0,20)	16	0,32	0,40
[0,20;0,24)	14	0,28	0,68
[0,24;0,28)	7	0,14	0,82
[0,28;0,32)	6	0,12	0,94
[0,32;0,36]	3	0,06	1,00
∑	50	1

Замечания к составлению табл. 2

1. Запись интервалов начинается с xmin и продолжается до тех пор, пока не войдёт xmax .

2.Просматривая по табл. 1 исходные данные признака X в порядке записи, проставляют (во втором столбце табл. 2) точки в интервале, которому соответствует данное значение X . Подсчитав количество проставленных точек, определим частоту, соответствующую данному интервалу.

3.В интервал включаются значения большие или равные нижней границе и меньшие верхней границы интервала.

4.Отношение частоты к общему числу наблюдений определяет час-

тость p*i = mni .

5. Накопленная частость интервала определяется как сумма частостей предшествующих и данного интервала [1, гл.15, п.7; 2, гл.9, п.2].

Б. Вычисление числовых характеристик

Таблица 3

Расчёт числовых характеристик

xi	mi	xi mi	xi − x	(xi − x)2	(xi − x)2 mi
0,14	4	0,56	-0,08	0,0064	0,0256
0,18	16	2,88	-0,04	0,0016	0,0256

16

Продолжение табл. 3 Расчёт числовых характеристик

0,22	14	3,08	0	0	0
0,26	7	1,82	0,04	0,0016	0,0112
0,30	6	1,80	0,08	0,0064	0,0384
0,34	3	1,02	0,12	0,0144	0,0432
∑	50	11,16			0,1440

Замечания к табл. 3 1. В первом столбце записаны середины интервалов, например, для

первого интервала x1 = 0,12 + 0,16 = 0,14 .

2

2. В третьем столбце результаты перемножения соответствующих значений первого и второго столбца. Вычисляем выборочную среднюю

	x =	∑xi mi	=	11,16	= 0,2238 ≈ 0,22 .
				50
		n

3. В четвёртом столбце разности между значениями xi и выборочным средним x .

4.В пятом столбце записываются квадраты значений четвёртого столбца.

5.В шестом столбце записаны результаты перемножения соответствующих значений второго и пятого столбцов. Вычислим выборочную

дисперсию	Db =	∑(xi	− x)2		mi	=	0,1440	≈ 0,0029	и среднее квадратиче-
			n				50
ское отклонение σx =			Db	=	0,0029 ≈ 0,053.

Пример 2. Построить теоретическую кривую нормального распределения по данным примера 1. Проверить по критерию Пирсона правильность выбранной гипотезы при уровне значимости α = 0,05.

Решение. Для построения нормальной кривой рассчитываем теоретические частоты mi по формуле

mi = nh ϕ(ti ),

σx

	где ti =	xi − x	, ϕ(t)=	1	e−	t 2		n - объём выборки, h - шаг интервала.
						2 ,
				2π
		σx

17

Составим расчётную таблицу

		Расчёт теоретических частот						Таблица 4
xi	mi	ti =	xi − 0,22			ϕ(ti )	mi =	50 0,04ϕ(ti )
				0,053
								0,053
0,14	4	-1,51				0,1276	5
0,18	16	-0,75				0,3011	11
0,22	14	0				0.3989	15
0,26	7	0,75				0,3011	11
0,30	6	1,51				0,1276	5
0,34	3	2,26				0,0310	1
∑	50						48

Замечания к табл. 4

1. Значения ϕ(ti ) находят по прил. 1 [1, с. 461; 2, с. 324] «Таблица зна-

чений функции ϕ(x)=	1	e−	x 2
				». При этом учитывают, что
			2
	2π

ϕ(− x)= ϕ(x). Для x > 3,99 ϕ(x)= 0 .

2.Теоретические частоты округляют до целых значений.

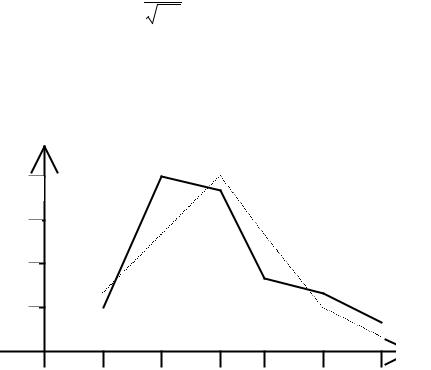
Построим полигоны эмпирических и теоретических частот производительности труда рабочих

m i mi

16

12

8

4

xi

0,14		0,18		0,22		0,26		0,3		0,34

Пунктирной линией построен полигон теоретических частот, а сплошной линией - полигон эмпирических частот.

18

Проверим согласованность теоретического и эмпирического распределения по критерию Пирсона

χ2 = ∑r (mi − mi )2 . p i =1 mi

		Расчёт величины χp2				Таблица 5
xi	mi	mi		mi − mi	(mi − mi )2	(mi − mi )2
						mi
0,14	4	5		4	16	1
0,18	20	16
	16	11
0,22	14	15		-1	1	0,07
0,26	7	11		-4	16	1,45
0,30	6	5		1	1	0,166
0.34	9	6
	3	1
∑	50	48				2,686
Замечание к табл. 5
Если число наблюдений			(частота mi ) в интервале меньше 5, то ин-

тервал объединяется с соседним и их частоты складываются. В этом случае и соответствующие им теоретические частоты mi также надо

сложить.

По прил. 5 « Критические точки распределения χ2 » [1, с. 465; 2, с.

329] находим χтабл2 (k,α), где α = 0,05 - уровень значимости, k - число степеней свободы, k = r − 3 = 4 − 3 = 1 (r - число интервалов после объе-

динения), χтабл2 (1;0,05)= 3,8. Так как χp2 = 2,686 меньше χтабл2 (1;0,05)= 3,8,

то различия между теоретическими и эмпирическими частотами незначимы.

Вывод. Производительность труда рабочих при проходке штрека распределяется по нормальному закону и имеет функцию плотности

	1		−(x−0,22)2
f (x)=		2π	e 2(0,053)2 .
	0,053

19

Пример 3. Найти доверительный интервал для оценки математического ожидания нормального распределения с надёжностью γ = 0,95 по

значениям x = 0,22; σx = 0,053; n = 50 , полученным в первом примере.

Решение. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии генеральной совокупности определяется по формуле

x −	s	tn, γ < a < x +	s	tn, γ .
	n		n
Для γ = 0,95, n = 50 по прил. «Таблица значений tγ = t(γ,n)» [1, с. 464;

2, с. 328] определяем tγ = t(0,95;50)= 2,009.

Определяем исправленную дисперсию s2 :

s2 = Db n		n − 1	= 0,0029	50	= 0,00295;
				50 − 1
s =	s2 =	0,00295 = 0,054;
s	tn, γ =	0,054 2,009 ≈		0,015;
n
		50
0,22 − 0,015 < a < 0,22 + 0,015;					0,205 < a < 0,235 .

Пример 4. При уровне значимости α = 0,08 проверить нулевую гипотезу H0: M(X)= M(Z) при конкурирующей гипотезе H1: M(X)≠ M(Z),

если z = 0,24;	D(Z)= 0,01;	m = 60 взяты из генеральной совокупности
Z , а x = 0,22;	D(X)= 0,029;	n = 50 берём из первого примера.

Решение. Вычисляем расчётное значение Z - критерия. Так как дисперсии генеральных совокупностей известны, то

x − z

0,22 − 0,24

≈ 1,33.

Zp =

=

D(Z)

D(X)

0,0029 0,01

+

+

50

60

n

m

Определяем критическую точку из равенства

Φ(Zkp )=

1 − α

=

1 − 0,08

= 0,46 .

2

2

z2

По прил. 2 «Таблица значений функции Φ(x)=

1

x

−

∫e

2

dz »

2π

0

[2, с. 462] по значению функции 0,46 определяем табличное (критическое) значение аргумента Zkp = 1,75 . Сравним Zp = 1,33 и Zkp = 1,75 . Так