§ 1 Криволинейные интегралы и их приложения

§ 1 Криволинейные интегралы и их приложения.

п.1 Кривые на плоскости и в пространстве
Пусть в пространстве задана ДСК.
Опр.1.1 Простой кривой L в пространстве называется множество точек M (x,y,z ),
координаты которых удовлетворяют уравнениям
x = x (t ), y = y (t ), z = z (t ) ,	(1.1)

где x (t ), y (t ), z (t ) − непрерывные функции переменной t , заданные на отрезке [α; β], причем разным значениям t соответствуют разные точки

M (x,y,z ).

Уравнения (1.1) называются параметрическими уравнениями кривой в пространстве Oxyz . Кривые на плоскости Oxy определяются уравнениями (1.1) в

которые не входит функция z = z (t ). Примеры.

1) x = cost,	y = sin t, z	= t , t [0; 2π] − один виток винтовой линии в
пространстве;		[0; 2π] − единичная окружность на плоскости
2) x = cost,	y = sin t , t
Oxy с центром O (0; 0; 0 ).
Говорят, что уравнения (1.1) задают замкнутую кривую, если значениям t			= α и
t = β соответствует одна точка M (x,y,z ).
Векторная функция
	r (t ) = x (t ) i + y (t ) j + z (t ) k		(1.2)

называется вектором кривой L или векторным уравнением кривой L .

Если для каждого t [α; β] из начала координат откладывать вектор r (t ), то

кривая L получатся как множество концов этих векторов. В этом случае говорят, что кривая есть годограф вектор-функции r = r (t ).

Опр. 1.2 Кривая r = r (t ) называется гладкой на [α; β], если на [α; β] существует r ′(t ) и r ′(t ) ≠ 0 для всех t [α; β]. Простая кривая называется кусочногладкой на [α; β], если отрезок [α; β] можно разделить на конечное число частей, на каждом из которых кривая гладкая.

Опр. 1.3 Кривая называется ориентированной, если задан порядок следования точек на этой кривой при возрастании параметра от α к β . Ориентацию кривой можно

сменить, введя новый параметр, например, по формуле τ = β + α −t .

Замкнутую кривую на плоскости ориентируют обычно так, чтобы при обходе кривой против часовой стрелки область ограниченная этой кривой, оставалась слева.

Для гладкой кривой ориентация определяется естественным образом выбором единичного направляющего вектора касательной, так как имеет место

Теорема 1.1 В каждой точке гладкой кривой существует касательная. Производная r ′(t ) направлена по этой касательной в сторону возрастания параметра.

п.2 Криволинейный интеграл 1-го рода. Его свойства и вычисление.

Пусть L кусочно-гладкая кривая в пространстве, заданная уравнениями (1.1), и в каждой точке этой кривой определена непрерывная функция f (x,y, z ). Разобьем эту

кривую на n частей и обозначим длины этих частей через l1, l2,…, ln . Выберем на каждой части разбиения по одной точке M1, M2,…, Mn и найдем значения функции

f (x,y, z ) в этих точках.

Опр. 1.4 Интегральной суммой для функции f (x,y, z ) по кривой L называется

сумма произведений значений функции, вычисленных в выбранных точках, на длины соответствующих частей разбиения.

In = f (M1 ) l1 + f (M2 ) l2 + + f (Mn ) ln .

Будем производить разбиения так, чтобы max li → 0 и для каждого такого

разбиения будем составлять интегральные суммы. В результате получается бесконечная числовая последовательность интегральных сумм

I1, I2,…, In ,…

Опр. 1.5 Если существует конечный предел последовательности интегральных сумм при max li → 0 , не зависящий от способа разбиения и выбора точек, то этот предел называется криволинейным интегралом первого рода от функции f (x,y, z ) по

кривой L и обозначается ∫ f (x,y, z )dl .

		L
	Основные свойства криволинейного интеграла первого рода
1)	Для функций f1 (x,y, z ) и f2 (x,y, z ) и постоянных c1 и c2 выполняется равенство
	∫ [c1f1 (x,y, z ) +c2 f2 (x,y, z )]dl = c1 ∫ f1 (x,y, z )dl +c2 ∫ f2 (x,y, z )dl .
	L		L	L
2)	Если кривая L составлена из кривых L1 и L2 , то
	∫ f (x,y, z )dl = ∫ f (x,y, z )dl + ∫ f (x,y, z )dl .
	L	L1	L2
3)	Значение криволинейного интеграла на кривой не зависит от ориентации кривой
	∫ f (x,y, z )dl = ∫ f (x,y, z )dl .
	L+	L−

Вычисление криволинейного интеграла сводится к вычислению определенного интеграла. Для этого найдем dl . По теореме Пифагора получаем

dl = (dx )2 +(dy )2 +(dz )2 .

1) Пусть кривая задана уравнениями x = x (t ),y = y (t ), z = z (t ) . Тогда dl = (dx )2 +(dy )2 +(dz )2 = (xt′)2 +(yt′)2 +(zt′)2dt и

	t2
∫ f (x,y, z )dl = ∫ f (x (t ),y (t ), z (t )) (xt′)2 +(yt′)2 +(zt′)2dt ,		(1.3)
L	t1

где t = t1 соответствует началу кривой, а t = t2 − концу кривой.

2) Если кривая задана на плоскости Oxy уравнениями x = x (t ), y = y (t ) , то

	t2
∫ f (x,y )dl = ∫ f (x (t ),y (t )) (xt′)2 +(yt′)2dt .		(1.4)
L	t1
3) Если кривая задана на плоскости графиком функции y = y (x ) , то
dl = (dx )2 +(dy )2 =	1 +(y′)2dx и для интеграла получаем
	x2
∫ f (x,y )dl = ∫ f (x,y (x )) 1 +(y′)2dx .		(1.5)
L	x1

4) Если кривая задана на плоскости в полярной системе координат уравнением r = r (ϕ),

то x = r (ϕ) cos ϕ ,	y = r (ϕ) sin ϕ и dl = (dx )2 +(dy )2 =	r2 +(r ′)2dϕ .
Тогда	ϕ2
∫ f (x,y )dl = ∫ f (r (ϕ)cos ϕ,r (ϕ)sin ϕ) r2 +(r ′)2dϕ.		(1.6)
L	ϕ1

п.3 Приложения криволинейного интеграла первого рода

1) Вычисление длины дуги кривой

l = ∫ dl .

L

2) Вычисление массы материальной кривой с плотностью ρ = ρ(x,y, z ) :

	m = ∫ ρ(x,y, z )dl .
	L
3) Вычисление статических моментов материальной кривой
относительно оси Ox : Mx	= ∫ ρ(x,y, z )	y2	+ z2dl ,
	L
относительно оси Oy : My	= ∫ ρ(x,y, z )	x2	+ z2dl ,
	L
относительно оси Oz : Mz	= ∫ ρ(x,y, z )	x2 + y2dl .
	L

4)Вычисление координат центра масс материальной кривой xc = Mmx ,y = Mmy , z = Mmz .

5)Вычисление моментов инерции материальной кривой

относительно оси Ox : Ix	= ∫ ρ(x,y, z )(y2 + z2 )dl ,
	L
относительно оси Oy : Iy	= ∫ ρ(x,y, z )(x2 + z2 )dl ,
	L
относительно оси Oz : Iz	= ∫ ρ(x,y, z )(x2 + y2 )dl .
	L

Если кривая задана в плоскости Oxy , то в формулах отсутствует координата z .

Пример. Найти массу четверти эллипса x = a cos t, y = b sin t , расположенной в первом квадранте, если ρ(x,y ) = y .

Решение. Величина массы найдется по формуле m = ∫ ρ(x,y )dl . Вычислим этот

L

интеграл в с помощью Maple. Криволинейные интегралы в этой программе удобно вычислять с помощью специализированных функций пакета > VectorCalculus.

1)Сначала подгружаем пакет

> with(VectorCalculus):

2)С помощью специальной функции PathInt() данного пакета задаем интеграл с опцией 'inert' , чтобы интеграл не вычислялся автоматически.

> PathInt(y,[x,y] = Path( <a*cos(t),b*sin(t)>, t=0..Pi/2),'inert');

π

⌠

2

a

2

sin( t )

2

+ b

2

cos( t )

2

dt

b sin( t )

⌡0

3) Вычисляем интеграл, убрав опцию 'inert' и добавив условия на параметры a и b

> m=simplify(PathInt(y,[x,y] = Path( <a*cos(t),b*sin(t)>, t=0..Pi/2))) assuming a>0, b>0,a>b;

					−b	2	+ a	2
		b	−b2 + a2	b + a2 arcsin
	1					a
m =
	2			−b2 + a2

или, раскрывая скобки, получаем

> m=expand(rhs(%));

								−b	2	+ a	2
		2			b a	2
	b			1			arcsin		a
m =			+
	2			2			−b2 + a2

	b2			ba2 arcsin		a2	−b2
							a
Ответ: m =			+					.
		2			2 a2 −b2

п.4 Криволинейные интегралы второго рода

Пусть L кусочно-гладкая кривая в пространстве, заданная уравнениями (1.1), и в каждой точке этой кривой определена непрерывная вектор-функция

F (x,y, z ) = P (x,y, z ) i +Q (x,y, z ) j + R(x,y, z ) k .

Разобьем эту кривую на n частей и обозначим векторы, соединяющие точки разбиения через l1, l2,…, ln . Выберем на каждой части разбиения по одной точке

M1, M2,…, Mn и найдем значения вектор-функции F (x,y, z ) в этих точках.

Опр. 1.6 Интегральной суммой для вектор-функции F (x,y, z ) по кривой L

называется сумма скалярных произведений значений вектор-функции, вычисленных в выбранных точках, на векторы соответствующих звеньев частей разбиения.

In = F (M1 ) l1 + F (M2 ) l2 + + F (Mn ) ln .

Будем производит разбиения так, чтобы max | li |→ 0 и для каждого такого

разбиения будем составлять интегральные суммы. В результате получается бесконечная числовая последовательность интегральных сумм

I1, I2,…, In ,…

Опр. 1.7 Если существует конечный предел последовательности интегральных сумм при max | li |→ 0 , не зависящий от способа разбиения и выбора точек, то этот предел называется криволинейным интегралом второго рода от вектор-функции

F (x,y, z ) по кривой L и обозначается ∫ F (x,y, z ) dl .

L

	Основные свойства криволинейного интеграла второго рода
1)	Для вектор-функций F1 (x,y, z ) и F2 (x,y, z )			и постоянных c1 и c2 выполняется
равенство
			= c1	∫ F1 (x,y, z ) dl +c2	∫ F2 (x,y, z ) dl .
	∫ c1F1 (x,y, z )	+c2F2 (x,y, z ) dl
	L			L	L
2)	Если кривая L составлена из кривых L1 и L2 , то
	∫ F (x,y, z ) dl = ∫ F (x,y, z ) dl + ∫ F (x,y, z ) dl .
	L	L1	L2
3)	Значение криволинейного интеграла на кривой зависит от ориентации кривой
	∫ F (x,y, z ) dl = −∫ F (x,y, z ) dl .
	L+	L−

Вычисление криволинейного интеграла сводится к вычислению определенного интеграла. Для этого найдем dl . Раскладывая этот вектор по векторам канонического базиса, получаем dl = dx i +dy j +dz k . Тогда

F (x,y, z ) dl = P (x,y, z )dx +Q (x,y, z )dy + R(x,y, z )dz

и

∫ F (x,y, z ) dl = ∫ P (x,y, z )dx +Q (x, y, z )dy + R (x, y, z )dz

L L

1) Пусть кривая задана уравнениями x = x (t ),y = y (t ), z = z (t ) . Тогда

∫ F (x,y, z ) dl = ∫ P (x,y, z )dx +Q (x,y, z )dy + R(x,y, z )dz =

L L t2

= ∫ [P (x (t ),y (t ), z (t ))x ′(t ) +Q (x (t ),y (t ), z (t ))y′(t ) +

t1

+R(x (t ),y (t ), z (t ))z ′(t )]dt.

2)Если кривая задана на плоскости Oxy уравнениями x = x (t ), y = y (t ) , то

∫ F (x,y ) dl = ∫ P (x,y )dx +Q (x,y )dy =

L L t2

= ∫ [P (x (t ),y (t ))x ′(t ) +Q (x (t ),y (t ))y′(t )]dt

t1

3) Если кривая задана на плоскости графиком функции y = y (x ) , то

x2

∫ F (x,y ) dl = ∫ P (x,y )dx +Q (x,y )dy = ∫[P (x,y (x )) +Q (x,y (x ))y′(x )]dx .

L L x1

4) Если кривая задана на плоскости в полярной системе координат уравнением r = r (ϕ), то x = r (ϕ) cos ϕ, y = r (ϕ) sin ϕ. Тогда

∫ F (x,y ) dl = ∫ P (x,y )dx +Q (x,y )dy =

L L

ϕ2

= ∫ [P (r (ϕ)cos ϕ,r (ϕ)sin ϕ)(r ′(ϕ)cos ϕ −r (ϕ)sin ϕ)+

ϕ1

+Q (r (ϕ)cos ϕ, r (ϕ)sin ϕ)(r ′(ϕ)sin ϕ + r (ϕ)cos ϕ)]dϕ.

п.5 Механический смысл криволинейного интеграла второго рода

Работа силы - мера действия силы, зависящая от её модуля и направления и от перемещения точки приложения силы. Если сила F постоянна по модулю и направлению, а перемещение M0M1 = s прямолинейно (рис. 1), то работа определяется равенством

A =| F | | s | cos α,

F
M0 M α	M1

s

где α - угол между направлениями силы и перемещения. Если α < 90 , то A > 0 , а если 90 < α < 180 , то A < 0 ; если же α = 90 , т. е. если сила перпендикулярна перемещению, то A = 0 . Единицы измерения работы - джоуль, эрг (1 эрг = 10-7 Дж) и килограмм-сила на 1 метр (1 кгс·м = 9,81 Дж).

В общем случае для вычисления работы силы вводят понятие элементарной работы dA =| F | | ds | cos α где ds - вектор элементарного перемещения точки приложения

силы, a α- угол между силой и вектором элементарного перемещения, направленным в сторону перемещения точки.

F

M1

M0	α
	M

ds

В декартовых координатах ds = dx i +dy j +dz k ,

F = P (x,y, z ) i +Q (x,y, z ) j + R(x,y, z ) k , поэтому элементарная работа будет равна dA = P (x,y, z ) dx +Q (x,y, z ) dy + R (x,y, z ) dz

координаты точки её приложения.

Работа силы на конечном перемещении определяется как предел интегральной суммы соответствующих элементарных работ и при перемещении по кривой L выражается криволинейным интегралом второго рода

∫ F (x,y, z ) ds = ∫ P (x,y, z )dx +Q (x,y, z )dy + R(x,y, z )dz

L L

Таким образом, криволинейный интеграл второго рода определяет значение работы силы при перемещении по кривой точки единичной массы.

Отметим, что

1)для сил давления элементарная работа равна dA = pdV , где p давление, а dV изменение объема;

2)для потенциальных сил dA = dU или dA = −dΠ, гдеU - силовая функция, а

Π- потенциальная энергия системы, A =U1 −U0 или A = Π0 − Π1 гдеU0 , U1 , Π0 ,

Π1 - значения соответствующих величин в начальном и конечном положениях системы; в

этом случае работа не зависит от вида траекторий точек приложения сил; 3) При движении механической системы сумма работ всех действующих сил на

некотором перемещении этой системы равна изменению её кинетической энергии T на этом же перемещении, т. е. ∑Ai =T1 −T0 .

Понятие работы широко используется в механике и в других областях физики, а также в технике.

Для вычисления КИВР в пакете Maple применяются как стандартные методы вычисления интегралов, так и специальные функции.

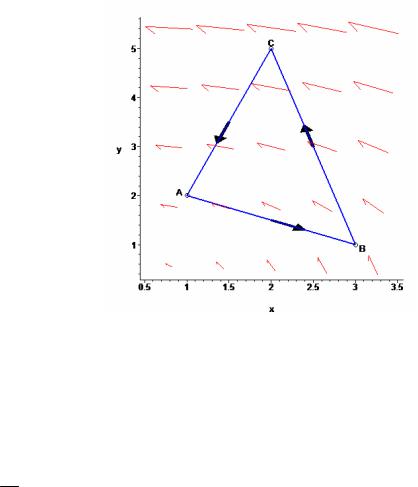
Пример. Вычислить криволинейный интеграл второго рода ∫ 2xdy − 3ydx ,

L

L – контур треугольника с вершинами A(1; 2), B (3; 1), C (2; 5 ), пробегаемый против

часовой стрелки.

Решение. Построим векторное поле, которое определяет КИВР и путь интегрирования 1) Загрузим пакет с функциями для вычисления криволинейных интегралов и пакет

построения графиков

>with(Student[VectorCalculus]): with(plots):

2) Определим векторное поле в виде графика и путь интегрирования. Дополнительно изобразим точки треугольника

>P1:=LineInt( VectorField( <-3*y,2*x > ), LineSegments( <1,2>,<3,1>,<2,5>,<1,2> ), output=plot ):

>P2:=textplot([1-0.05,2,A],align={ABOVE,LEFT}): T1:=pointplot([1,2],symbol=circle,symbolsize=14):

>P3:=textplot([3+0.05,1,B],align={BELOW,RIGHT}):

T2:=pointplot([3,1],symbol=circle,symbolsize=14):

>P4:=textplot([2,5+0.05,C],align={ABOVE}):

T3:=pointplot([2,5],symbol=circle,symbolsize=14):

>display(P1,P2,P3,P4,T1,T2,T3);

3) Вычисляем КИВР

> VectorCalculus[LineInt]( VectorField(<-3*y,2*x> ),

LineSegments( <1,2>,<3,1>,<2,5>,<1,2> ), inert )= LineInt( VectorField( <-3*y,2*x> ), LineSegments( <1,2>,<3,1>,<2,5>,<1,2> ));

⌠1	⌠1	⌠1	3 − 3 t dt =	35
	−14 + 2 t dt +	27 + 4 t dt +		2
⌡0	⌡0	⌡0

35

Ответ: 2 .

п.6 Формула Грина. Независимость криволинейного интеграла от пути интегрирования.

Если кривая L расположена на плоскости Oxy и замкнута, то КИВР обозначается в виде ∫ F (x,y ) dl = ∫ P (x,y )dx +Q (x,y )dy , а сама кривая L называется

L L

контуром.

Обозначим через D область, которую ограничивает контур L .

Теорема. 1.2 Пусть L замкнутая кусочно-гладкая кривая, ограничивающая область D , а функции P (x,y ) и Q (x,y ) непрерывны вместе со своими частными

∂P ∂Q

производными ∂y и ∂x в области D . Тогда имеет место формула

	(		)		(		)		∂Q		∂P
∫ P		x,y		dx +Q		x,y				−
								dy = ∫∫			dxdy .
L								D	∂x		∂y

Доказательство. Пусть контур L , может быть задан как уравнениями x = x1 (y ) ,

x = x2 (y ), c ≤ y ≤ d , x1 (y ) ≤ x2 (y ) , так и уравнениями y = y1 (x ) , y = y2 (x ) , a ≤ x ≤ b , y1 (x ) ≤ y2 (x ).

y

E

y2

(x )

B

x1 (y )

D

x2 (y )

A

C

y1 (x )

O

x

интеграл ∫∫ ∂∂Py dxdy

Вычислим

двойной

по

области

D с помощью повторного

интеграла

D

b

y2(x )

b

∫∫ ∂y

∫

dx

∫ ∂y

∫

[P (x,y

(x ))−P (x,y (x ))]dx

=

∂P dxdy =

∂P dy =

2

1

D

a

y (x )

a

1

b

b

= ∫ P (x,y2 (x ))dx − ∫ P (x,y1 (x ))dx = ∫ P (x,y )dx − ∫ P (x,y )dx =

a

a

AEB

ACB

= − ∫ P (x,y )dx − ∫ P (x,y

BEA ACB

Аналогично

∫∫ ∂∂Qx	d	x2(x )	∂∂Qx dx
	dxdy = ∫dy ∫
D	c	x1(x )
d		d

)dx = −∫ P (x,y )dx.

L

d

= ∫ [Q (x2 (y ),y )−Q (x1 (y ),y )]dy =

c

= ∫Q (x2 (y ),y )dy − ∫Q (x1 (y ),y )dy = ∫ P (x,y )dx − ∫ P (x,y )dx =

c c CBE CAE

= ∫ P (x,y )dx + ∫ P (x,y )dx = ∫Q (x,y )dy.

CBE EAC L

Вычитая из второго равенства первое, получаем формулу Грина в виде

∂Q	−	∂P			x,y		dx +Q		x,y		dy .
∫∫		dxdy = ∫ P		(		)		(		)
D ∂x		∂y	L

Теорема доказана.

В некоторых случаях величина КИВР не зависит от пути интегрирования, а зависит только от начальной и конечной точек. Укажем условия при которых это свойство выполняется.

Опр. 1.8 Плоская область D называется односвязной, если любой замкнутый контур, лежащий внутри этой области ограничивает часть плоскости, целиком принадлежащую области D .

Теорема 1.3 Пусть функции P (x,y ) и Q (x,y ) непрерывны вместе со своими

∂P ∂Q

частными производными ∂y и ∂x в замкнутой односвязной области D . Тогда

следующие четыре условия эквивалентны

1) для любой замкнутой кусочно-гладкой кривой L , расположенной в области D

∫ P (x,y )dx +Q (x,y )dy = 0 ;

L

2) для любых точек A и B области D значение интеграла ∫ P (x,y )dx +Q (x,y )dy

		AB
не зависит от пути, соединяющего точки A и B ;
3) выражение P (x,y )dx +Q (x,y )dy		представляет собой полный	дифференциал
некоторой функции F (x,y ), то есть
∂F	∂F
dF (x,y ) = ∂x dx + ∂y dy = P (x,y )dx +Q (x,y )dy ;
4) в области D выполняется условие	∂P	= ∂Q .
	∂y	∂x
(Шипачев В.С. Высшая математика, с 337-339)
Пример. Вычислить интеграл второго рода ∫ xydx + yzdy + zxdz			L – четверть
окружности x = cos t , y = sin t , z		L
	= t , пробегаемая в направлении возрастания

параметра t .

>with( Student[VectorCalculus] ):

>with(plots):

>P1:=LineInt( VectorField( <x*y,y*z,z*x> ),

Path( <cos(t),sin(t),t>,t=0..Pi/2 ), output=plot ):

>

P2:=textplot3d([1,0+0.1,0,A],align={BELOW,RIGHT},color=black):T1

:=pointplot3d([1,0,0],symbol=circle,symbolsize=14,color=black):

>P3:=textplot3d([0,1,1.7,B],align={BELOW,RIGHT},color=black):

T2:=pointplot3d([0,1,1.6],symbol=circle,symbolsize=14,

color=black):

>display(P1,P2,T1,P3,T2,axes=normal,orientation=[-10, 72]);