Анализ данных отчеты Катков / Prakticheskaya_rabota_2

Министерство образования и науки

Государственное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ

Методические материалы к выполнению практической работы №2 по дисциплине «Анализ и обработка данных» для студентов, обучающихся по специальности 080801 Прикладная информатика (в управлении)

Новокузнецк

2010

УДК 519.24: 681.3

С

Рецензент доктор технических наук, профессор кафедры информационных

технологий в металлургии СибГИУ С.Н. Калашников

С 37 Статистические характеристики: метод. указ. / Сост.: Т.В. Кораблина; Сиб. гос. индустр. ун-т. – Новокузнецк: СибГИУ, 2010 – 17 с.

Изложены основные теоретические и практические подходы и алгоритмы для оценки значений статистических характеристик случайной величины, рассчитываемых по экспериментальным данным.

Предназначены для студентов специальностей 080801 – Прикладная информатика (в управлении).

	СОДЕРЖАНИЕ
Введение.....................................................................................................		4
1.	Выборочное среднее...........................................................................	5
2.	Выборочная дисперсия и среднеквадратическое отклонение........	7
3.	Центральные моменты высоких порядков.......................................	8
Задание 1 .................................................................................................		9
4.	Доверительный интервал. Доверительная вероятность................	10
Задание 2 ...............................................................................................		17
СПИСОК ЛИТЕРАТУРЫ.......................................................................		18

3

Введение

Для решения задачи об оценке закона распределения случайной величины по экспериментальным данным необходим достаточно обширный статистический материал (порядка нескольких сотен значений). На практике же часто приходится иметь дело с весьма ограниченными выборками (несколько десятков). Такого количества отсчетов значений величины недостаточно, чтобы найти заранее неизвестный закон распределения. Этот материал может быть использован для определения статистических характеристик – важных числовых параметров случайной величины, которые в некоторой степени характеризуют наиболее важные свойства ее закона распределения. Такими статистическими характеристиками являются выборочное среднее, дисперсия и ряд других моментов более высокого порядка.

Другая задача прикладной статистики заключается в оценке неизвестных параметров закона распределения, когда сам закон заранее известен. Например, если известно, что случайная величина подчинена нормальному закону распределения, то по выборочным данным необходимо определить два параметра – математическое ожидание тх и среднеквадратическое отклонение σх. Если известно, что случайная величина подчинена закону Пуассона, то подлежит определению только один его параметр – математическое ожидание λ.

4

1. Выборочное среднее

Математическое ожидание или среднее значение – это число-

вая характеристика, определяющая положение случайной величины на числовой оси, т.е. указывает некоторое ориентировочное значение, около которого группируются все возможные значения случайной величины.

В качестве оценки математического ожидания, которую будем назвать выборочным средним, чаще всего используют арифметическое среднее, вычисленное по отсчетам значений случайной величины:

~		1	L
x	=		∑x(l)	(1)
		L l=1

x(ℓ) – отсчет ряда данных или значений случайной величины; ℓ – порядковый номер отсчета случайной величины;

L – объем выборки.

При увеличении объема выборки L величина ~x сходится по вероятности к математическому ожиданию т.

Для установления качества или «правильности» оценки используется три основных свойства.

1. Желательно, чтобы математическое ожидание оценки равнялось оцениваемому параметру:

M[ϕ~ ]= φ,

(2)

где M[·] – оператор математического ожидания или осреднения; ϕ~ – оценка параметра φ.

Если это свойство имеет место, то оценка называется несмещенной. 2. Желательно, чтобы среднеквадратичная ошибка данной оценки

была наименьшей среди всех возможных оценок:
	M[(ϕ~	– φ)2]≤ M[(ϕ~	– φ)2],	(3)
где ϕ~	1	i
	– исследуемая оценка;
1
ϕ~i	– любая другая оценка;

Если это свойство имеет место, то оценка называется эффективной. 3. Желательно, чтобы оценка сходилась к оцениваемому параметру с вероятностью, стремящейся к единице по мере увеличения раз-

мера выборки, т.е. для любого ε > 0:

limP[|ϕ~ −ϕ |>ε] = 0,

(4)

L→∞

где P[·] – вероятность события [·].

5

Если это так, то оценка называется состоятельной. Достаточным для выполнения условия (4) является условие:

lim M [(ϕ~ −ϕ)2 ] = 0,	(5)
L→∞

Рассмотрим оценку среднего значения ~x . Математическое ожидание выборочного среднего равно:

~

1

L

1

L

1

M[x ] = M

∑x(l)

=

M ∑x(l)

=

(Lmx ) = mx

(6)

L

L

L l=1

l=1

Следовательно, согласно (2) оценка среднего значения несмещенная. Среднеквадратическая ошибка выборочного среднего ~x равна:

~

2

1 L

2

1

L

2

M[(x

−m

x

)

]= M

∑

x(l) −m

=

M

x(l) −m

. (7)

2

x

∑

x

L l=1

L

l=1

Будем считать, что отсчеты случайной величины независимы, поэтому математические ожидания членов, содержащих произведения, равны нулю. Поэтому

~

2

1

L

2

1

2

σx2

M[(x

−m

x

)

]=

M

x(l) −m

=

(Lσ

x

)=

.

(8)

2

2

∑

x

L

L

l=1

L

Следовательно, согласно (34) оценка ~x состоятельна. Эффективность или неэффективность оценки среднего значения

зависит от вида закона распределения величины. Можно доказать, что если величина распределена по нормальному закону, то оценка среднего значения ~x будет эффективной. Для других законов распределения это может быть иначе.

В качестве оценки для выборочного среднего в том случае, когда закон распределения случайной величины близок к нормальному, можно использовать медиану. Кроме того, медиана является помехозащищенной оценкой среднего, это свойство обусловлено алгоритмом

еерасчета:

1.Строится вариационный ряд, т.е. значения случайной величины упорядочиваются по возрастанию или убыванию.

2.Если количество отсчетов величины нечетное, то в качестве значения медианы берется центральный отсчет вариационного ряда

L
med = x		,	(9)
	2

где [ ] – результат деления нацело. Если количество отсчетов вариационного ряда четное, то в качестве значения медианы берется сред-

6

нее арифметическое двух центральных отсчетов:

		L		L
	x			+ x		+1
med =		2		2			,	(10)
				2

2. Выборочная дисперсия и среднеквадратическое отклонение

Дисперсия – это характеристика рассеивания случайной величины около ее среднего значения. Дисперсия имеет размерность квадрата случайно величины. Оценить дисперсию можно по формуле:

~	1	L	~	2
d x =		∑	(x(l) − x )		.	(11)
	L l=1

Для удобства характеристики рассеивания используют величину, размерность которой совпадает с размерностью случайной величины, такой характеристикой является среднеквадратическое отклонение, которая определяется как корень квадратный из дисперсии:

σ~х =

~

(12)

dx .

Рассмотрим свойства оценки дисперсии. Математическое ожи-

дание оценки дисперсии равно

~

1

L

~

2

1

L

~

2

M[d

] = M

∑

(x(l)

− x )

=

M ∑

(x(l) − x )

(13)

L

L l=1

l=1

В свою очередь

L

~ 2

L

~

2

= ∑(x(l) −mx

∑(x(l) − x )

+ mx − x )

=

L

l=1

l=1

L

L

2

~

~

−mx )

2

= ∑

(x(l) −mx ) −

2(x −mx )∑

(x(l) −mx )+∑

(x

=

l=1

L

l=1

l=1

2

−

~

~

~

2

= ∑(x(l) −mx )

2(x −mx )L(x −mx )+ L(x

−mx )

=

l=1

L

2

~

2

= ∑(x(l) −mx )

− L(x

−mx )

l=1

d x

2

~

2

Так как M[(x(l) −mx )

]= dx

и

M[(x

−mx ) ]=

, то

L

~

1

L −1

M[dx ]=

(Ld x −dx )=

d x

L

L

(14)

(15)

7

~

Следовательно, оценка dx смещена. Для получения несмещенной

оценки, согласно формуле (15), следует использовать видоизмененную формулу (11) для оценки выборочной дисперсии

~	1	L	~ 2
dx =		∑(x(l) − x ) .		(16)
	L −1l=1

Величина, рассчитываемая по формуле (16), представляет собой несмещенную оценку дисперсии dx.

Для проверки состоятельности оценки дисперсии выразим ее через второй начальный момент

~	1	L	(x(l))	2	~2
d x =		∑			− x	.	(17)
	L l=1

Первый член в правой части есть среднее арифметическое L квадрата значений случайной величины. Он сходится по вероятности ко второму начальному моменту α2. Второй член сходится по вероятности к квадрату математического ожидания. Вся величина (17) сходится по вероятности к дисперсии dx. Это означает что оценка выбо-

~

рочной дисперсии dx состоятельная.

~

Оценка для дисперсии dx не является эффективной. Однако, в

случае нормального закона распределения она является «асимптотически эффективной», то есть при увеличении объема выборки L отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

На практике вместо формулы (16) можно применять формулу

~			1	L	2	~2		L
d	x	=		∑	(x(l))	− x				.	(18)
								L −1
		L l=1

3. Центральные моменты высоких порядков

Коэффициент асимметрии или третий центральный момент – числовая величина характеризующая асимметричность закона распределения случайной величины. Если распределение симметрично относительно среднего значения, то коэффициент асимметрии равен нулю. В этом случае равны нулю и все нечетные центральные моменты. Оценка выборочного коэффициента асимметрии определяется по формуле:

8

		1	L	~ 3
			∑	(x(l) − x )
	~	L			.	(19)
			l=1
	βx =
				σ~х3

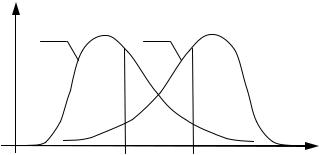
На рисунке 1 показаны два асимметричных распределения с положительным значением коэффициентом распределения (кривая 1) и отрицательным (кривая 2).

f(x)

1 2

m1

m2

x

Рисунок 1 – Асимметричные распределения: 1 – коэффициент асимметрии βх > 0, 2 – коэффициент асимметрии βх < 0

Эксцесс или четвертый центральный момент – числовая величина характеризующая «крутость» закона распределения случайной величины, т.е. островершинность или плосковершинность распределения, по сравнению с нормальным законом.

Оценка выборочного эксцесса определяется по формуле:

	1	L	~ 4
~		∑	(x(l) − x )
	L l=1			−3.	(20)
γx =
			σ~х3

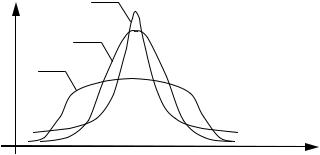
Число 3 вычитается из отношения потому, что для нормального закона распределения это отношение равно трем. Таким образом, для нормального закона распределения эксцесс равен нулю. Для более островершинных кривых по сравнению с нормальным законом эксцесс положительный, для более плосковершинных – отрицательный (рисунок 2).

Задание 1

Для данных, по которым в практической работе №1 строилась гистограмма, рассчитать значения выборочных оценок статистических характеристик: среднего, медианы, дисперсии, среднеквадратического отклонения, коэффициента вариации, коэффициента асимметрии и эксцесса.

9

f(x) 1 2

3

x

Рисунок 2 – Распределения с различными значениями эксцесса γх:

1–γх > 0; 2 – γх = 0; 3 – γх < 0

4.Доверительный интервал. Доверительная вероятность

Оценка неизвестного параметра а одним числом называется точечной. В ряде задач требуется не только найти для параметра а подходящее численное значение, но и оценить его точность и надежность. Требуется знать, к каким ошибкам может привести замена параметра а его точечной оценкой а~ и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы.

Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка а~ в значительной мере случайна и приближенная замена а на а~ может привести к серьезным ошибкам.

Чтобы дать представление о точности и надежности оценки а~ , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.

Пусть для параметра а получена из опыта несмещенная оценка а~ Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность р (например, р = 0,9; 0,95 или 0,99) такую, что событие с вероятностью р можно считать практически достоверным, и найдем такое значение ε, для которого

P(| a −a |<ε) = р	(21)
~

Тогда диапазон практически возможных значений ошибки, возникающей при замене а на а~ , будет ±ε; большие по абсолютной величине ошибки будут появляться только с малой вероятностью α = 1р (рисунок 3).

10