
[ Будылин ] Методическое пособие по высшей математике в третьем семестре с примерами решения типовых задач
.pdf
|
|
|
|
|
|
! "
!" #$%! !$! ! &'$( ) % & * +$ $ * $* * * ( ,- !&'. / " #
#$
%
$0
1223 0
& % " '
% % % % ( )%*%
+ " ,
*-#%
# *-#%
!" #$%! !$! ! &'$( ) % & * + $ $ * $ * * * ( ,- !&'.
/ " # 4$5 1223
) $
' . / ' &
0 ' +' .
0 % 1 + +
' " + 0 %
+ $
Методическое пособие по высшей математике в третьем семестре с примерами решения типовых задач
Будылин А.М.
Содержание
1 |
Введение |
2 |
|
2 |
Криволинейный интеграл 1 рода |
3 |
|
|
2.1 |
Теоретический материал . . . . . . . . . . . . . . . . . |
3 |
|
2.2 |
Примеры решения задач . . . . . . . . . . . . . . . . . |
6 |
3 |
Поверхностный интеграл 1 рода |
9 |
|
|
3.1 |
Теоретический материал . . . . . . . . . . . . . . . . . |
9 |
|
3.2 |
Примеры решения задач . . . . . . . . . . . . . . . . . |
11 |
4 |
Дифференциальные формы |
14 |
|
4.1Теоретический материал . . . . . . . . . . . . . . . . . 14
4.1.1Формы и их внешнее произведение . . . . . . 14
4.1.2Дифференцирование форм . . . . . . . . . . . 15
4.1.3Замена переменных . . . . . . . . . . . . . . . 16
4.1.4 Точные и замкнутые формы . . . . . . . . . . |
17 |
4.2 Примеры решения задач . . . . . . . . . . . . . . . . . |
18 |
5 Криволинейный интеграл 2 рода |
23 |
5.1Теоретический материал . . . . . . . . . . . . . . . . . 23
1
5.2 Примеры решения задач . . . . . . . . . . . . . . . . . 25
6 Поверхностные интегралы 2 рода |
27 |
6.1Теоретический материал . . . . . . . . . . . . . . . . . 27
6.2Примеры решения задач . . . . . . . . . . . . . . . . . 29
7 Геометрия поверхностей |
31 |
7.1Теоретический материал . . . . . . . . . . . . . . . . . 31
7.2Примеры решения задач . . . . . . . . . . . . . . . . . 32
1 Введение
Данное учебное пособие посвящено основным практическим вопросам курса математического анализа на физическом факультете в третьем семестре, а именно разбору типовых задач по темам: кратные и поверхностные интегралы, дифференциальные уравнения, геометрия поверхностей. В целях замкнутости изложения по каждой из данных тематик приводится краткая теоретическая справка.
Главным побудительным мотивом к написанию предлагаемого пособия явился переход от устного экзамена к письменному. Не затрагивая здесь мотивов, собственно оправдывающих эту реформу экзамена, отметим, что в рамках письменного экзамена по математическому анализу на первый план выступает умение студентафизика решать стандартные практические задачи.
Стоит отдельно подчеркнуть, что материал пособия, посвященный алгебре и интегрированию дифференциальных форм, весьма бедно представлен в общедоступной отечественной литературе.
Пособие рекомендуется студентам всех трех потоков второго курса.
2

2Криволинейный интеграл 1 рода
2.1Теоретический материал
Путь в Rn — это непрерывное отображение : [a; b] ! Rn. Значения функции (t) называются точками пути . В координатах путь описывается равенствами
x1 = x1(t) ; : : : xn = xn(t) ; |
t 2 [a; b] : |
Точка (a) называется началом пути , точка (b) — его концом. Если начало и конец пути совпадают, путь называется замкнутым. Если вектор-функция непрерывно дифференцируема и 0(t) =6 0, путь называется гладким. Производная 0 называется скоростью пути . Путь эквивалентен пути , если = ', где ' — непрерывно дифференцируемая функция и '0 > 0. Класс эквивалентных между собой путей называется ориентированной кривой. Кривая в Rn — это такое подмножество в Rn, которое является образом (множеством точек) некоторого пути. Путь , определяющий кривую , называется ее параметризацией. Кривая называется гладкой или замкнутой, если таковым свойством обладает ее параметризация. Каждой гладкой кривой отвечает ровно две ориентированных гладких кривых. Они называются ее ориентациями. Выбранная ориентация называется положительной, другая — отрицательной. Ориентация гладкой кривой может быть определена выбором непрерывного единичного касательного векторного поляк кривой. Последний определяется параметрически равенствами
0(t) P = (t) ; (P ) = j 0(t)j ;
где — параметризация ориентированной кривой. Если кривая не замкнута, ее ориентация может быть определена выбором начала и конца кривой.
Интеграл от функции f по гладкой кривой с параметризацией
3
:
Z
[a; b] ! Rn определяется равенствами |
|
|
|
|
|||
f(P ) dl = Z |
f(P ) dl = Za b f( (t))j 0(t)j dt |
|
|
|
|||
|
|
Za |
b |
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
1 |
n0 |
|||
|
= |
|
f(x1(t); : : : xn(t)) |
x02 |
(t) + : : : + x 2(t) dt : |
||
Определение не зависит от параметризации кривой, в частности, от ее ориентации. Так определенный интеграл обладает свойством линейности относительно интегрируемой функции и свойством аддитивности относительно кривой интегрирования. На кусочно гладкие кривые интеграл распространяется по аддитивности. Интеграл от f = 1 по кривой (пути ) называется длиной данной кривой (пути):
l( ) = l( ) = Z dl = Z dl :
Физический смысл интеграла по длине дуги
M( ) = Z dl
— масса кривой с линейной плотностью . Координаты центра тяжести такой кривой определяются равенствами
|
xi dl |
|
|
|
; i = 1; : : : n : |
xi = R |
|
|
M( ) |
|
|
Интегралы
Z rk dl ;
4
где r — расстояние от точки массивной кривой до некоторой фиксированной точки, прямой или плоскости, называются моментами порядка k данной кривой относительно данной точки, оси или плоскости. Моменты первого порядка называются также статическими, моменты второго порядка называются моментами инерции.
5

2.2Примеры решения задач
Задача Найти массу винтовой линии
x = a cos t ; y = a sin t ; z = bt ; 0 6 t 6 2 ;
если плотность в каждой ее точке равна квадрату аппликаты.
Решение. Обозначим винтовую линию через . Тогда
|
2 |
|
|
|
|
|
|
|
|
M( ) = Z |
z2 dl = Z0 |
(bt)2p |
|
|
dt |
|
|
|
|
( a sin t)2 + (a cos t)2 + b2 |
|
|
|
||||||
|
|
|
|
|
|
|
8 3 |
|
|
|
|
|
= b2 |
p |
: |
||||
|
|
|
|
|
|||||
|
|
|
|
a2 + b2 |
3 |
||||
Задача Найти момент инерции однородной полуокружности x2 + y2 = R2; y > 0, относительно оси OX.
Решение. Обозначим полуокружность через , плотность через , а искомый момент через I. Параметризация окружности может быть определена равенствами
|
x = R cos t ; y = R sin t ; |
0 6 t 6 |
: |
|
|
|
Тогда |
|
|
|
|
|
|
I = Z |
y2 dl = Z0 (R sin t)2p |
|
|
|
|
|
( R sin t)2 |
+ (R cos t)2 dt |
|
||||
|
|
= R3 |
1 cos 2t dt = R3 |
: |
||
|
|
|
Z0 |
2 |
|
|
|
|
|
2 |
|
||
6

Задача Найти статический момент дуги параболы y = x2 ; 0 6 x 6 1; относительно оси OY .
Решение. Обозначим дугу параболы через , плотность через . Тогда
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = (1 + 4x2)3=2 |
|
1= |
5p5 1 |
: |
||
x dl = |
x |
p |
1 + 4x2 |
|
||||||
Z |
Z0 |
6 |
|
0 |
6 |
|
||||
Задача Найти координаты центра тяжести однородной полуокружности
x2 + y2 + z2 = R2 ; y = x ; x > 0 :
Решение. Обозначим полуокружность через , плотность через , искомые координаты через x0; y0; z0. По соображениям симметрии
x0 = y0 ; z0 = 0 :
Зададим параметризацию равенствами
R |
sin ; |
R |
|
|
|
: |
|||
x = p2 |
y = p2 sin ; z = R cos ; 0 |
6 |
6 |
||||||
|
|
|
|
|
|
|
|
||
Тогда
|
|
|
|
|
|
M( ) = Z |
R2 |
R2 |
|||
|
|||||
dl = Z0 r 2 cos2 + |
2 cos2 + R2 sin2 d |
||||
= R Z d = R
0
7
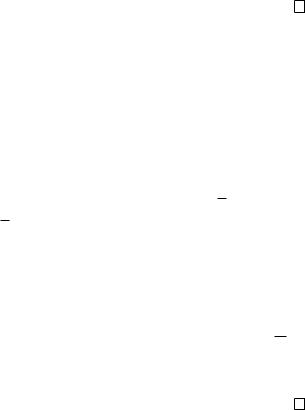
и
|
x dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
|
|
|
Rp2 |
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|||||||
x0 = R |
|
= |
|
|
|
|
sin R d = |
|
|
( cos ) |
|
= |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
R Z0 |
|
|
|
|
|
|
|
|
|||||||
M( ) |
|
p2 |
|
p2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
Задача Найти момент инерции однородной окружности x2 + y2 + z2 = R2 ; x + y + z = R
относительно плоскости XOZ.
Решение. Обозначим окружность через , плотность через , искомый момент через I. Отметим, что данная окружность описана около равностороннего треугольника со стороной Rp2, следова-
тельно, ее радиус равен Rq2 . Тогда
3
I = Z |
y2 dl = Z |
|
|
|
R2 |
Z |
|
R2l( ) |
y2 dl = |
3 Z |
(x2+y2+z2) dl = |
3 |
dl = |
3 |
= 2 R3 r2 : 3 3
8
