
- •Задания и методические указания
- •080503.65 Антикризисное управление (351000)
- •© Гоу впо « Российский государственный профессионально-педагогический
- •Указания к выполнению контрольной работы
- •Содержание контрольной работы
- •Из генеральной совокупности , распределенной по нормальному закону, извлечена выборка. Требуется:
- •Из генеральной совокупности , распределенной по нормальному закону, извлечена выборка. Требуется:
- •Уровень значимости
- •Литература
- •Подписано в печать Формат 60х84/16. Бумага для множ. Аппаратов
Из генеральной совокупности , распределенной по нормальному закону, извлечена выборка. Требуется:
1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
2. Построить полигон относительных частот;
3. Построить график эмпирической функции распределения;
4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
5. С надежностью
![]() найти доверительные интервалы для
оценки математического ожидания и
среднего квадратического отклонения
изучаемого признака генеральной
совокупности.
найти доверительные интервалы для
оценки математического ожидания и
среднего квадратического отклонения
изучаемого признака генеральной
совокупности.
1.0.
![]()
-
5,6
5,8
5,0
5,4
5,2
5,8
5,2
5,6
5,6
5,6
5,4
5,0
5,4
5,8
5,4
5,6
5,4
5,2
5,4
5,4
5,6
5,0
6,0
5,8
5,2
5,8
5,6
5,8
6,0
5,2
5,8
6,0
6,2
5,4
6,2
5,6
6,0
5,6
5,2
5,6
Составим
вариационный ряд. Напомним, что
вариационным рядом называется
последовательность наблюдаемых
значений признака ![]() ,
расположенных в неубывающем порядке
,
расположенных в неубывающем порядке
![]() ,
,![]() ,…,
,…,![]() ,
где
,
где
![]()
![]() …
…![]() .
Следовательно, в нашей задаче вариационный
ряд запишется так:
.
Следовательно, в нашей задаче вариационный
ряд запишется так:
-
5,0
5,0
5,0
5,2
5,2
5,2
5,2
5,2
5,2
5,4
5,4
5,4
5,4
5,4
5,4
5,4
5,4
5,6
5,6
5,6
5,6
5,6
5,6
5,6
5,6
5,6
5,6
5,8
5,8
5,8
5,8
5,8
5,8
5,8
6,0
6,0
6,0
6,0
6,2
6,2
Составим статистический ряд распределения данной нам выборки
-
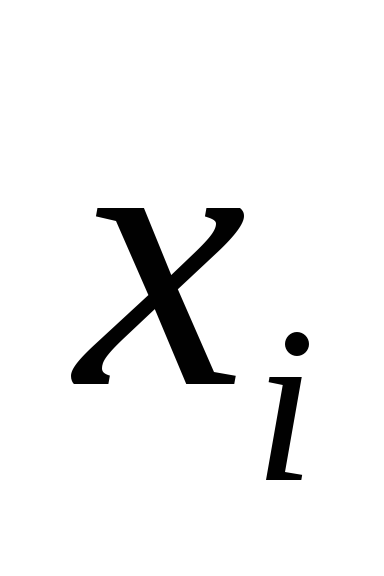
5,0
5,2
5,4
5,6
5,8
6,0
6,2
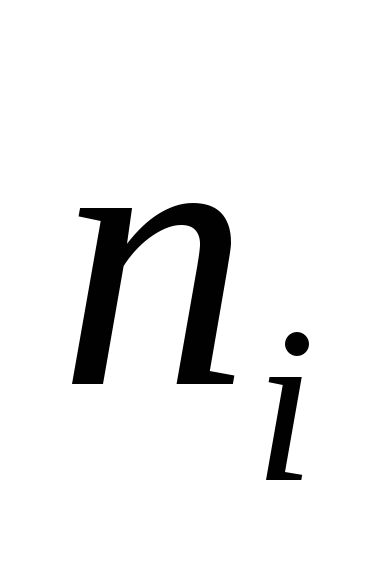
3
6
8
10
7
4
2
![]() -
варианты,
-
варианты,
![]() -
частоты.
-
частоты.
Найдем объем выборки
![]() .
.
Относительная
частота вычисляется по формуле
![]() .
.
Запишем выборочный ряд распределения
-
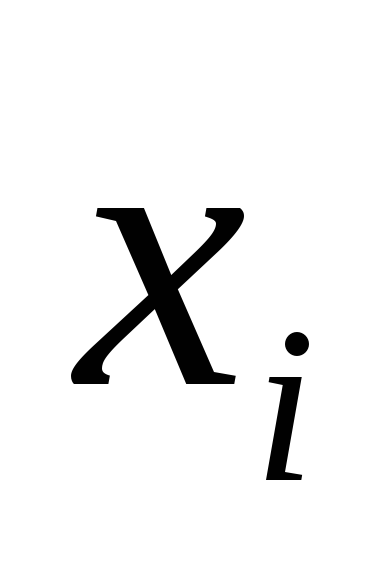
5,0
5,2
5,4
5,6
5,8
6,0
6,2
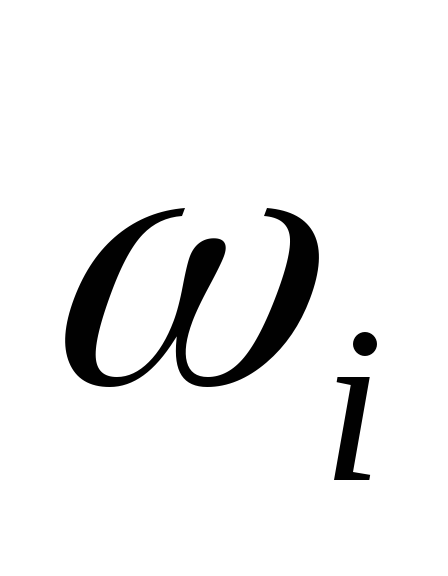
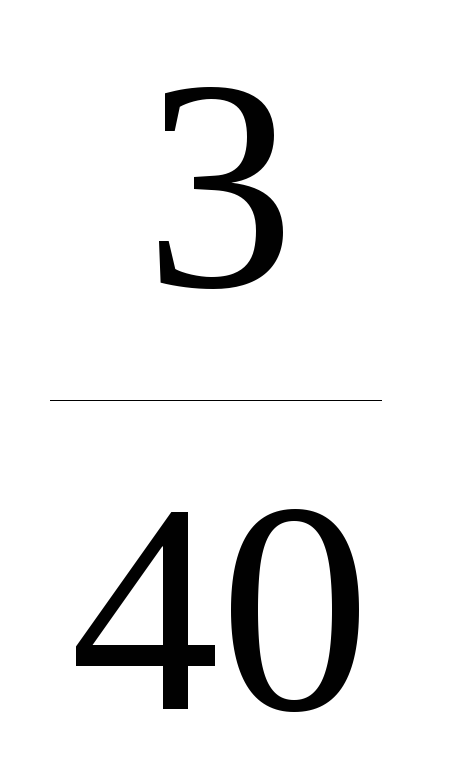
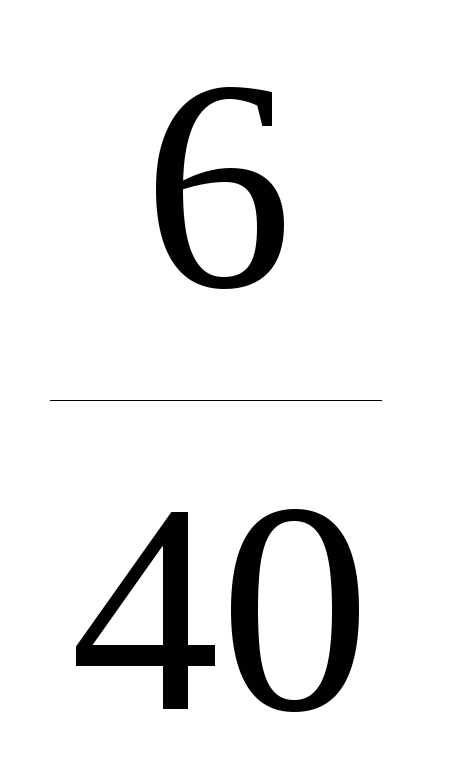
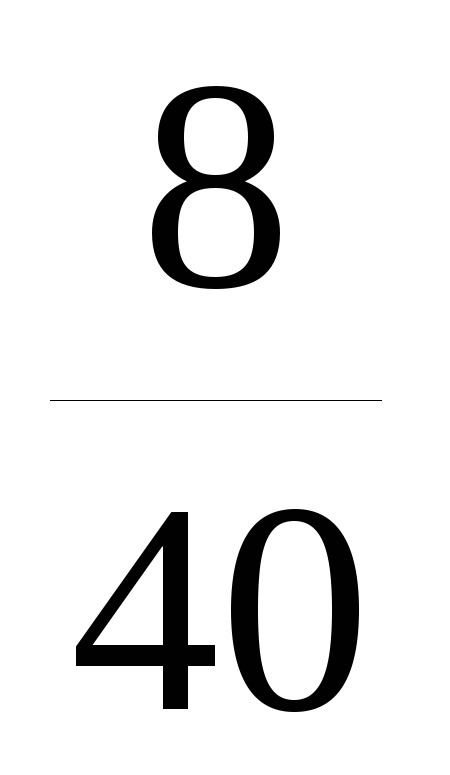
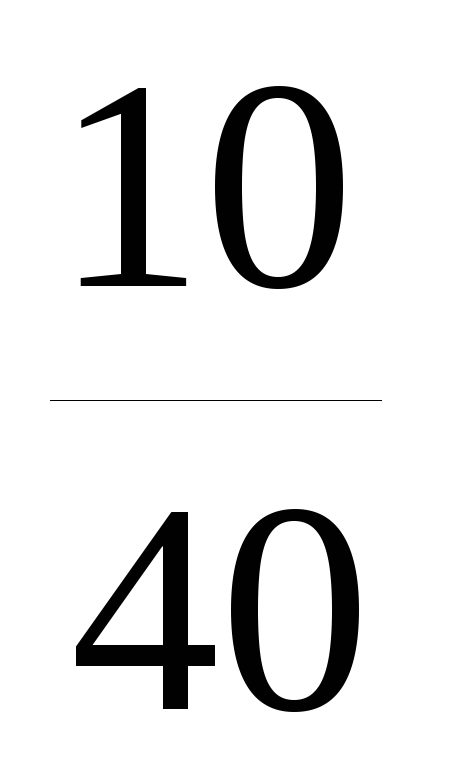
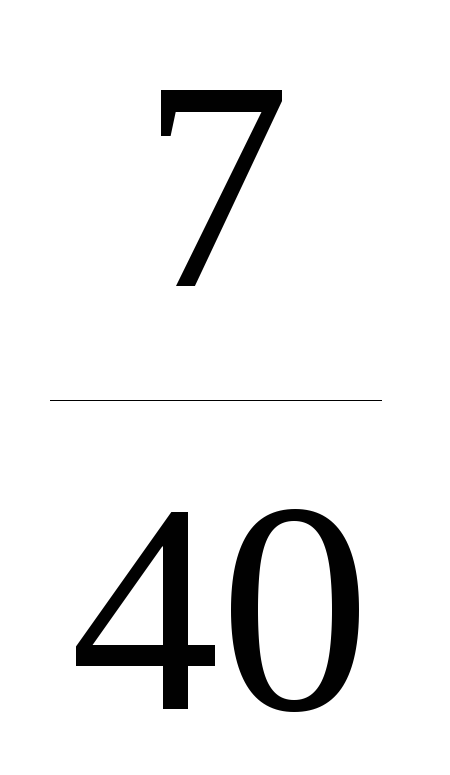

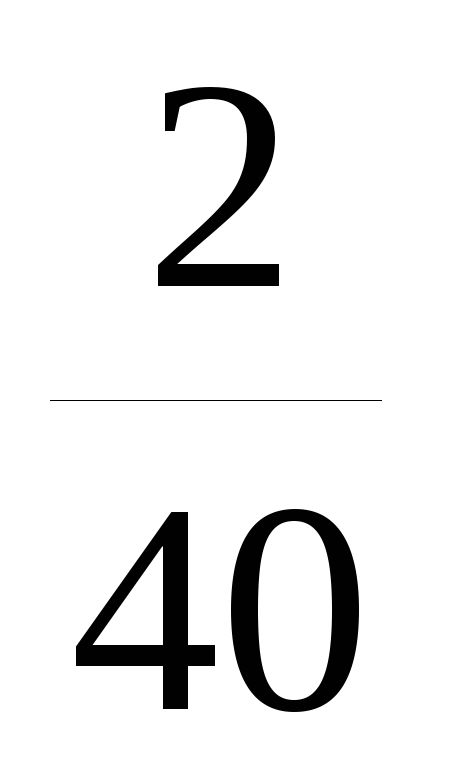
![]()
![]() .
.
Размах
выборки
![]() ,
т.е. в нашем случае
,
т.е. в нашем случае![]() .
.
П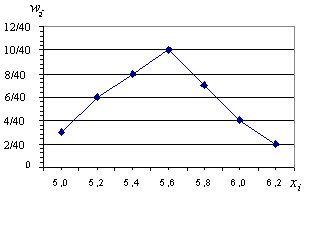 остроим
полигон относительных частот
остроим
полигон относительных частот
Вычислим выборочную среднюю
![]() =
=
=
=![]() (
(![]() )=
)=![]() =5,56.
=5,56.
Построим
график эмпирической функции распределения![]() где
где![]() (
(![]() число вариант, меньших, чем значение
аргумента
число вариант, меньших, чем значение
аргумента
![]() ).
).
В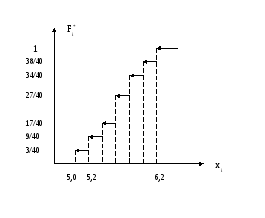 ычислим
выборочную дисперсию
ычислим
выборочную дисперсию![]() ,
где в нашем случае
,
где в нашем случае![]() =
=![]() (
(![]() )=
)=![]() =31,012
=31,012
![]()
![]() .
.
Найдем выборочное среднее квадратическое отклонение
![]()
Вычислим
"исправленную" дисперсию
![]() ,
которая выражается формулой
,
которая выражается формулой
![]() (в нашем случае
(в нашем случае
![]() )
)
и
"исправленное" среднее квадратическое
отклонение
![]() .
.
Модой
![]() называется варианта с наибольшей
частотой, т.е. в нашей задаче
называется варианта с наибольшей
частотой, т.е. в нашей задаче![]() .
Медиана
.
Медиана![]() - варианта, которая делит вариационный
ряд на две части, равные по числу вариант,
т.е. в нашей задаче
- варианта, которая делит вариационный
ряд на две части, равные по числу вариант,
т.е. в нашей задаче![]() .
.
Найдем с надежностью =0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
Так как по условию задачи генеральная совокупность x распределена по нормальному закону и объем выборки равен n=40, то искомый доверительный интервал для оценки математического ожидания имеет вид
![]() ,
,
где
![]() - среднее квадратическое отклонение, а
величинаt
определяется по таблице значений функции
Лапласа из равенства
- среднее квадратическое отклонение, а
величинаt
определяется по таблице значений функции
Лапласа из равенства
![]() .
.
Следовательно,
в нашем случае последнее равенство
принимает вид
![]() .
Из этого равенства по таблице значений
интегральной функции Лапласа
.
Из этого равенства по таблице значений
интегральной функции Лапласа![]() находим значениеt=1,96.
Величина
находим значениеt=1,96.
Величина
![]() была найдена ранее:
была найдена ранее:![]() и
и![]() .
.
Вычислим
![]() .
.![]() .
.
Учитывая,
что
![]() ,
доверительный интервал для оценки
математического ожидания запишется
,
доверительный интервал для оценки
математического ожидания запишется![]() или,
окончательно,
или,
окончательно,![]() .
.
Доверительный
интервал для среднего квадратического
отклонения нормально распределенной
случайной величины находится по формуле
![]() ,
гдеs
- "исправленное" среднее квадратическое
отклонение, а
находится по формуле
,
гдеs
- "исправленное" среднее квадратическое
отклонение, а
находится по формуле
![]() ,
где величинаq
определяется по специальной таблице
значений функции
,
где величинаq
определяется по специальной таблице
значений функции
![]() .
.
Найдем
![]() для нашей конкретной задачи:
для нашей конкретной задачи:
q=q(0,95;40)=0,24;
=sq=0,3210,24=0,077.
Следовательно,
![]() или
окончательно
или
окончательно![]() .
.
На этом решение задачи 1 закончено.
Задача 2.
Для выборки,
извлеченной из генеральной совокупности
и представленной интервальным рядом
(в первой строке указаны интервалы
значений
![]() исследуемого количественного признакаX
генеральной совокупности; во второй –
частоты
исследуемого количественного признакаX
генеральной совокупности; во второй –
частоты
![]() ,
т.е. количество элементов выборки,
значения
,
т.е. количество элементов выборки,
значения![]() признака которых принадлежат указанному
интервалу), требуется:
признака которых принадлежат указанному
интервалу), требуется:
1) Построить полигон относительных накопленных частот (кумулятивную кривую);
2) Построить гистограмму частот и гистограмму относительных частот;
3) Найти выборочную среднюю, выборочную дисперсию, моду и медиану;
4) Проверить на
уровне значимости
![]() гипотезу о нормальном распределении
признака
гипотезу о нормальном распределении
признака![]() генеральной совокупности по критерию
согласия Пирсона;
генеральной совокупности по критерию
согласия Пирсона;
5) В случае
согласованности с нормальным распределением
найти с надежностью
![]() доверительные интервалы для оценки
математического ожидания и среднего
квадратического отклонения признака
доверительные интервалы для оценки
математического ожидания и среднего
квадратического отклонения признака![]() генеральной совокупности.
генеральной совокупности.
2.0.
|
|
3-5 |
5-7 |
7-9 |
9-11 |
11-13 |
13-15 |
15-17 |
|
|
10 |
70 |
450 |
970 |
860 |
330 |
60 |
![]() .
.
В нашем случае n=2750.Тогда на основе данной таблицы построим интервальный статистический и интервальный выборочный ряды распределения, сведенные в одну таблицу.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
3-5 |
5-7 |
7-9 |
9-11 |
11-13 |
13-15 |
15-17 |
|
|
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
|
10 |
70 |
450 |
970 |
860 |
330 |
60 |
|
|
0,0036 |
0,0255 |
0,1636 |
0,3527 |
0,3127 |
0,12 |
0,0218 |
|
|
0,0036 |
0,0291 |
0,1927 |
0,5454 |
0,8581 |
0,9781 |
1 |
П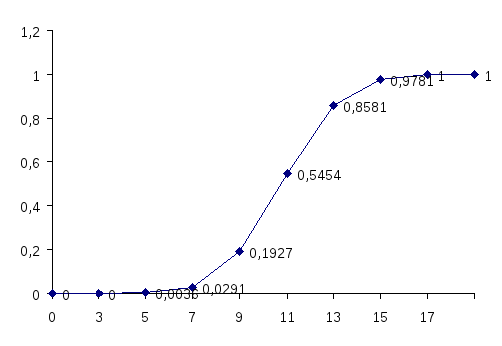 остроим
полигон относительных накопленных
частот (кумулятивную кривую);
остроим
полигон относительных накопленных
частот (кумулятивную кривую);
Построим гистограмму частот.
В
нашем случае исследуемый признак X
может принимать значения на отрезке
[3;17]. Интервальная группировка выполнена
таким образом, что длина каждого интервала
равна h=2.
Площадь прямоугольника, построенного
на i-ом
интервале, должна равняться
![]() .
Это значит, что высотаi-го
прямоугольника будет
.
Это значит, что высотаi-го
прямоугольника будет
![]() .
.
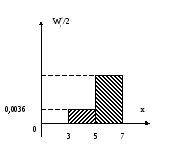
Н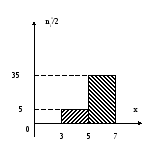 а
остальных интервалах прямоугольники
строятся аналогично.
а
остальных интервалах прямоугольники
строятся аналогично.
Если
высотуi-го
прямоугольника определим как
![]() ,
то получим гистограмму относительных
частот, которую можно рассматривать
как аналог дифференциальной функции
распределения в теории вероятностей.
,
то получим гистограмму относительных
частот, которую можно рассматривать
как аналог дифференциальной функции
распределения в теории вероятностей.
Для того, чтобы найти выборочную среднюю, воспользуемся формулой
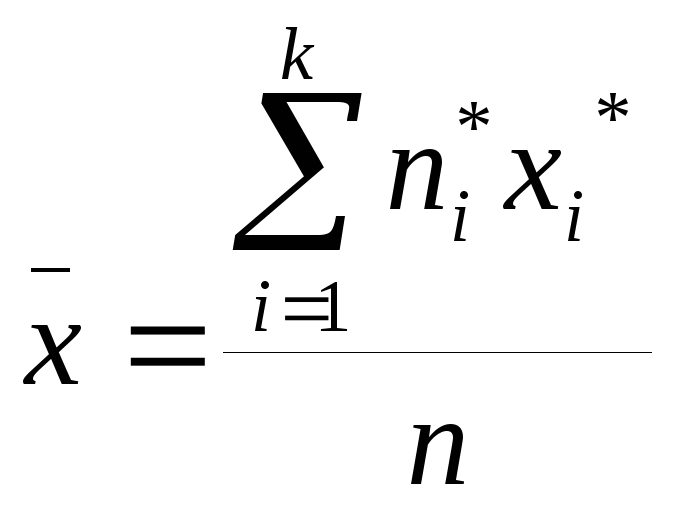 ,
где k
- количество интервалов, n
- объем выборки.
,
где k
- количество интервалов, n
- объем выборки.
![]() .
.
Для
вычисления выборочной дисперсии
воспользуемся формулой
![]() .
В случае интервальной группировки
.
В случае интервальной группировки![]() находится по формуле
находится по формуле![]()
![]()
=![]() .
.
Теперь можно окончательно вычислить выборочную дисперсию
![]() .
.
Найдем выборочное среднее квадратическое отклонение
![]() .
.
Отыщем выборочный коэффициент вариации
![]() .
.
Найденное значение выборочного коэффициента вариации дает наглядное представление о степени относительного рассеяния исследуемого признака.
Отыщем
значения "исправленной" дисперсии
и "исправленного" среднего
квадратического отклонения
![]() ,
,
![]() .
.
Для
отыскания моды
![]() в случае интервальной группировки
используем формулу
в случае интервальной группировки
используем формулу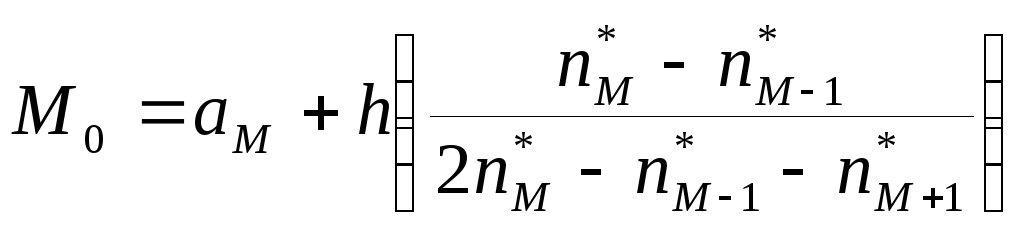 ,
где
,
где![]() -
левая граница интервала, имеющего
наибольшую интервальную частоту,h
- шаг (длина интервала группировки),
-
левая граница интервала, имеющего
наибольшую интервальную частоту,h
- шаг (длина интервала группировки),
![]() ,R
- размах выборки, k
- количество интервалов,
,R
- размах выборки, k
- количество интервалов,
![]() - наибольшая интервальная частота,
- наибольшая интервальная частота,![]() - интервальная частота интервала,
расположенного слева от интервала с
наибольшей интервальной частотой,
- интервальная частота интервала,
расположенного слева от интервала с
наибольшей интервальной частотой,![]() - интервальная частота интервала,
расположенного справа от интервала с
наибольшей интервальной частотой.
- интервальная частота интервала,
расположенного справа от интервала с
наибольшей интервальной частотой.
В
нашем случае
![]() .
.
Значение
медианы
![]() для случая интервальной группировки
отыщем по формуле
для случая интервальной группировки
отыщем по формуле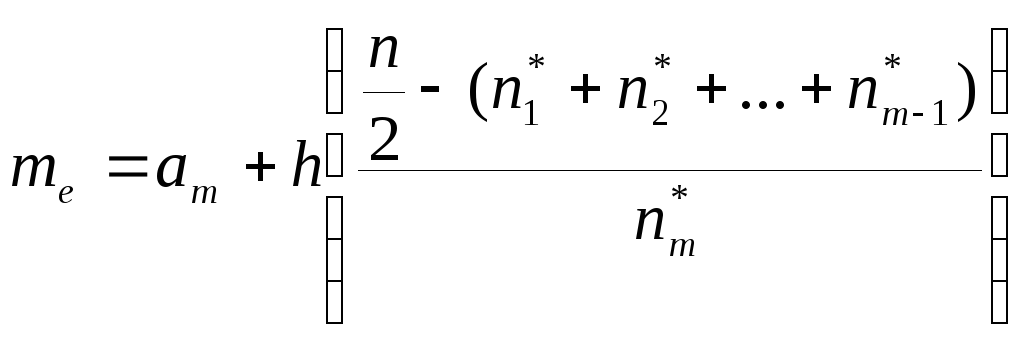 ,
где
,
где![]() - левая граница интервала, содержащего
медиану,n
- объем выборки, h
- шаг,
- левая граница интервала, содержащего
медиану,n
- объем выборки, h
- шаг,
![]() - интервальная частота интервала,
содержащего медиану,
- интервальная частота интервала,
содержащего медиану,![]() - интервальные частоты всех интервалов,
расположенных слева от интервала,
содержащего медиану.
- интервальные частоты всех интервалов,
расположенных слева от интервала,
содержащего медиану.
Найдем
значение медианы
![]() для нашей конкретной задачи .
для нашей конкретной задачи .
Далее
начнем суммировать интервальные частоты
слева направо до тех пор пока сумма
интервальных частот не превзойдет
![]() .Номер последней прибавленной частоты
будет совпадать с номером интервала,
содержащего медиану распределения:
10+70+450+970=1500>1375. Следовательно,
.Номер последней прибавленной частоты
будет совпадать с номером интервала,
содержащего медиану распределения:
10+70+450+970=1500>1375. Следовательно,![]() =9,
=9,![]() .
.
Проверим
на уровне значимости =0,05
гипотезу
![]() о нормальном распределении признакаx
генеральной совокупности по критерию
согласия Пирсона.
о нормальном распределении признакаx
генеральной совокупности по критерию
согласия Пирсона.
Для
нашей задачи все условия применимости
метода Пирсона выполняются:
![]() ,
для любого интервала
,
для любого интервала![]() .
.
Проверка гипотезы нормальности по критерию Пирсона основана на сравнении эмпирического и гипотетического распределений, точнее, на сравнении эмпирических и гипотетических интервальных частот. Мера близости между ними оценивается статистикой Пирсона:
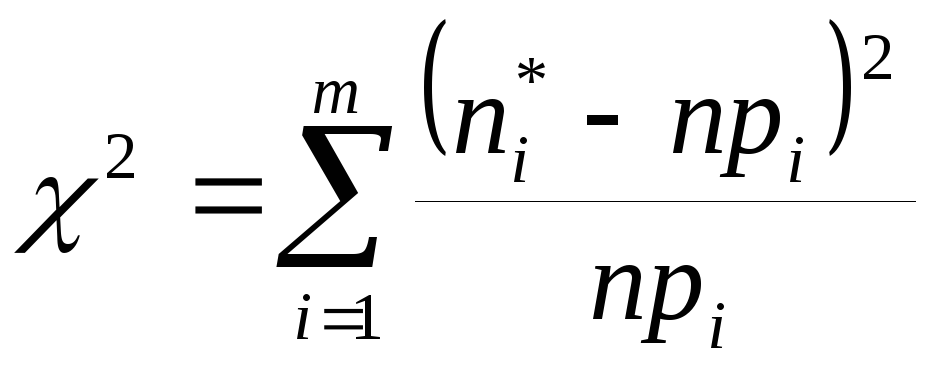 ,
где
,
где
![]() - интервальные (эмпирические) частоты,
- интервальные (эмпирические) частоты,![]() - интервальные теоретические частоты,
- интервальные теоретические частоты,![]() - теоретические вероятности попадания
переменнойx
в i-ый
интервал группировки,
- теоретические вероятности попадания
переменнойx
в i-ый
интервал группировки,
![]() ,
,![]() - левая границаi-го
интервала,
- левая границаi-го
интервала,
![]() - правая границаi-го
интервала.
- правая границаi-го
интервала.
При
этом теоретические вероятности
![]() рассчитываются в предположении
нормальности распределения случайной
величиныx
по формуле:
рассчитываются в предположении
нормальности распределения случайной
величиныx
по формуле:
![]() ,
где
,
где
![]() и функция
и функция![]() есть плотность стандартного нормального
распределения, таблица значений которой
приведена в приложении 2.
есть плотность стандартного нормального
распределения, таблица значений которой
приведена в приложении 2.
Вычисление
наблюдаемого значения статистики
Пирсона
![]() организуем в форме расчетной таблицы.
Для заполнения таблицы нам понадобятся
величины
организуем в форме расчетной таблицы.
Для заполнения таблицы нам понадобятся
величины![]() ,
,![]() ,
,![]() .
.
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(3;5) |
4 |
10 |
6,785 |
3,182 |
0,0025 |
0,0023 |
6,325 |
3,675 |
13,506 |
2,135 |
|
2 |
(5;7) |
6 |
70 |
4,785 |
2,244 |
0,0325 |
0,0305 |
83,87 |
-13,87 |
192,516 |
2,295 |
|
3 |
(7;9) |
8 |
450 |
2,785 |
1,306 |
0,1691 |
0,1586 |
436,15 |
13,85 |
191,823 |
0,440 |
|
4 |
(9;11) |
10 |
970 |
0,785 |
0,368 |
0,3726 |
0,3495 |
961,12 |
8,875 |
78,766 |
0,082 |
|
5 |
(11;13) |
12 |
860 |
1,215 |
0,570 |
0,3391 |
0,3181 |
874,78 |
-14,78 |
218,301 |
0,250 |
|
6 |
(13;15) |
14 |
330 |
3,215 |
1,508 |
0,1276 |
0,1197 |
329,18 |
0,825 |
0,681 |
0,002 |
|
7 |
(15;17) |
16 |
60 |
5,215 |
2,446 |
0,0198 |
0,0186 |
51,15 |
8,85 |
78,322 |
1,531 |
|
|
|
|
2750 |
|
|
|
0,9973 |
|
|
|
6,735 |
Следовательно,
![]() .
Заданный уровень значимости
.
Заданный уровень значимости![]() ,
количество интервалов группировки
,
количество интервалов группировки![]() ,
и потомуp=1-=0,95
и число степеней свободы k=m-3=4.
,
и потомуp=1-=0,95
и число степеней свободы k=m-3=4.
Теперь
по таблице критических точек распределения
![]() отыщем значение
отыщем значение![]() .
.
Сравним
значения
![]() и
и![]() .
Имеем 6,735<9,5 , следовательно,
.
Имеем 6,735<9,5 , следовательно,![]() <
<![]() .
Поэтому гипотезу о нормальном распределении
признакаx
принимаем. В этом случае необходимо
найти с надежностью =0,95
доверительные интервалы для оценки
математического ожидания и среднего
квадратического отклонения признака
x
генеральной совокупности. Пример
нахождения доверительных интервалов
разобран при решении задачи 1 (пятый
вопрос).
.
Поэтому гипотезу о нормальном распределении
признакаx
принимаем. В этом случае необходимо
найти с надежностью =0,95
доверительные интервалы для оценки
математического ожидания и среднего
квадратического отклонения признака
x
генеральной совокупности. Пример
нахождения доверительных интервалов
разобран при решении задачи 1 (пятый
вопрос).
Таким образом, решение задачи 2 полностью разобрано.
Задача 3.
Проведите сравнительный анализ результатов педагогического эксперимента в контрольных и экспериментальных группах, используя критерий однородности Пирсона.
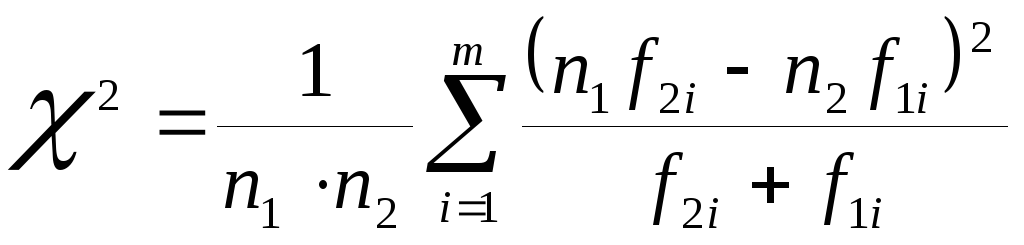 ,
где
,
где
![]() и
и![]() .
.
Уровень
значимости положите
![]()
3.0.
|
Значение
варианты
|
|
|
|
|
|
Частота
появления
|
|
|
|
|
|
Частота
появления
|
|
|
|
|
Проведем сравнительный анализ результатов педагогического эксперимента в контрольных и экспериментальных группах, используя критерий однородности Пирсона:
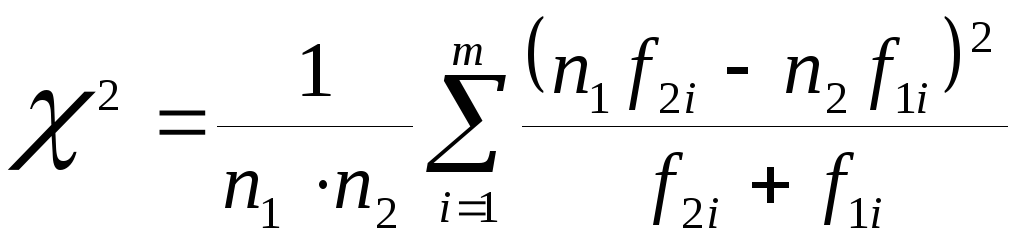 ,
где 2, 3, 4, 5 - вариационный ряд (оценки,
выставляемые по результатам проведения
контрольных работ),
,
где 2, 3, 4, 5 - вариационный ряд (оценки,
выставляемые по результатам проведения
контрольных работ),
![]() - частота появленияi-ой
варианты в экспериментальной группе,
- частота появленияi-ой
варианты в экспериментальной группе,
![]() - частота появленияi-ой
варианты в контрольной группе,
- частота появленияi-ой
варианты в контрольной группе,
![]() -
объем выборки в экспериментальной
группе,
-
объем выборки в экспериментальной
группе,![]() -
объем выборки в контрольной группе,m=4
- количество различных значений варианты
(количество интервалов группировки),
k=m-1=3
- количество степеней свободы.
-
объем выборки в контрольной группе,m=4
- количество различных значений варианты
(количество интервалов группировки),
k=m-1=3
- количество степеней свободы.
Найдем
![]() и
и![]() .
.![]() =27+25+28+9=89,
=27+25+28+9=89,![]() =9+5+18+10=42.
=9+5+18+10=42.
Теперь
вычислим
![]() .
.
![]() =
=![]() =8,6.
=8,6.
По
таблице критических точек распределения
![]() ,
приведенной в приложении 3, для числа
степеней свободыk=3
и уровня значимости =0,05
находим значение
,
приведенной в приложении 3, для числа
степеней свободыk=3
и уровня значимости =0,05
находим значение
![]() =7,81.
=7,81.
Так
как
![]() >
>![]() (8,6>7,81), то согласно правилу принятия
решения, делаем вывод, что существуют
достоверные различия между результатами
проведения контрольных работ в
экспериментальной и контрольной группах
на уровне надежности=1-=1-0,05=0,95.
(8,6>7,81), то согласно правилу принятия
решения, делаем вывод, что существуют
достоверные различия между результатами
проведения контрольных работ в
экспериментальной и контрольной группах
на уровне надежности=1-=1-0,05=0,95.
На этом решение задачи 3 закончено. Приведенный пример с небольшими изменениями взят из работы [7].
Задача 4.
Исследуется
зависимость коэффициента усвоения
знаний, выраженного в процентах (![]() %)
от уровня посещаемости занятий (
%)
от уровня посещаемости занятий (![]() %)
в группе из четырнадцати учащихся (
%)
в группе из четырнадцати учащихся (![]() -
порядковый номер учащегося). Статистические
данные приведены в таблице.
-
порядковый номер учащегося). Статистические
данные приведены в таблице.
Требуется:
1)
Найти оценки параметров линейной
регрессии
![]() на
на![]() .
Построить диаграмму рассеяния и нанести
прямую регрессии на диаграмму рассеяния.
.
Построить диаграмму рассеяния и нанести
прямую регрессии на диаграмму рассеяния.
2)
На уровне значимости
![]() проверить гипотезу о согласии линейной
регрессии с результатами наблюдений.
проверить гипотезу о согласии линейной
регрессии с результатами наблюдений.
3)
С надежностью
![]() найти доверительные интервалы для
параметров линейной регрессии.
найти доверительные интервалы для
параметров линейной регрессии.
4.0.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
53 |
40 |
46 |
39 |
35 |
29 |
75 |
31 |
68 |
66 |
60 |
54 |
55 |
59 |
|
|
36 |
30 |
32 |
29 |
27 |
23 |
47 |
19 |
44 |
42 |
40 |
39 |
33 |
37 |
Найдем
точечные статистические оценки
![]() и
и![]() параметров
параметров![]() и
и![]() линейной регрессииY
на X:
линейной регрессииY
на X:
![]() .
.
Для
уравнения прямой регрессии
![]() по статистическим данным таблицы 4.0
найдем оценки
по статистическим данным таблицы 4.0
найдем оценки
![]() и
и![]() ее параметров методом наименьших
квадратов. Применим известные формулы
ее параметров методом наименьших
квадратов. Применим известные формулы
![]() ,
где
,
где
![]() ,
,![]() ;
;
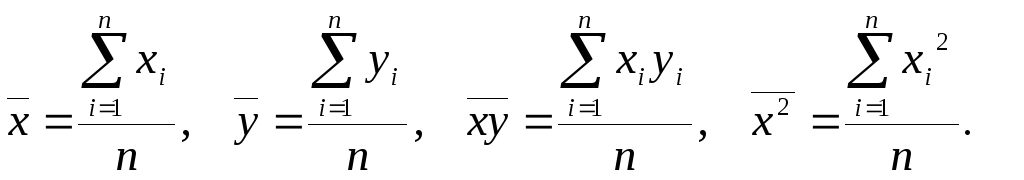
Вычисления
![]() организуем в форме следующей расчетной
таблицы:
организуем в форме следующей расчетной
таблицы:
|
i |
|
|
|
|
|
|
1 |
53 |
36 |
1908 |
2809 |
1296 |
|
2 |
40 |
30 |
1200 |
1600 |
900 |
|
3 |
46 |
32 |
1472 |
2116 |
1024 |
|
4 |
39 |
29 |
1131 |
1521 |
841 |
|
5 |
35 |
27 |
945 |
1225 |
729 |
|
6 |
29 |
23 |
667 |
841 |
529 |
|
7 |
75 |
47 |
3525 |
5625 |
2209 |
|
8 |
31 |
19 |
589 |
961 |
361 |
|
9 |
68 |
44 |
2992 |
4624 |
1936 |
|
10 |
66 |
42 |
2772 |
4356 |
1764 |
|
11 |
60 |
40 |
2400 |
3600 |
1600 |
|
12 |
54 |
39 |
2106 |
2916 |
1521 |
|
13 |
55 |
33 |
1815 |
3025 |
1089 |
|
14 |
59 |
37 |
2183 |
3481 |
1369 |
|
|
710 |
478 |
25705 |
38700 |
17168 |
|
|
50,714 |
34,143 |
1836,071 |
2764,286 |
1226,286 |
Таким
образом,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Далее вычисляем ковариации
![]() ;
;
![]() ;
;
![]() ;
;
и по указанным выше формулам находим
![]() ;
;
![]() .
.
В результате получаем уравнение прямой регрессии
![]() .
.
Проверим согласованность выбранной линейной регрессии с результатами наблюдений. Для этого решим следующую задачу проверки статистической гипотезы.
На
заданном уровне значимости
![]() выдвигается
гипотеза
выдвигается
гипотеза![]() об отсутствии линейной статистической
связи. Для проверки выдвинутой гипотезы
используется коэффициент детерминации
об отсутствии линейной статистической
связи. Для проверки выдвинутой гипотезы
используется коэффициент детерминации![]() и применяется статистика ФишераF.
и применяется статистика ФишераF.
В
случае парной линейной регрессии
коэффициент детерминации
![]() равен квадрату выборочного коэффициента
корреляции Пирсона, т.е.
равен квадрату выборочного коэффициента
корреляции Пирсона, т.е.![]() .
.
Статистика
F
выражается формулой
![]() и при условии справедливости гипотезы
имеет классическое распределение Фишера
с
и при условии справедливости гипотезы
имеет классическое распределение Фишера
с![]() и
и![]() степенями свободы.
степенями свободы.
В соответствии с приведенными формулами вычисляем коэффициент детерминации и наблюдаемое значение статистики Фишера:
![]() ,
,
![]() .
.
Критическое
значение статистики Фишера
![]() находим по таблице квантилей распределения
Фишера, исходя из равенства
находим по таблице квантилей распределения
Фишера, исходя из равенства![]() ,
гдеp=1-
(порядок квантили),
,
гдеp=1-
(порядок квантили),
![]() и
и![]() .
В данном случае
.
В данном случае![]() .
.
Сравниваем
между собой наблюдаемое и критическое
значения статистики Фишера. Так как
![]() ,
то выдвинутая гипотеза
,
то выдвинутая гипотеза![]() решительно отвергается, что свидетельствует
о согласии линейной регрессивной связи
с результатами наблюдений.
решительно отвергается, что свидетельствует
о согласии линейной регрессивной связи
с результатами наблюдений.
Так
как линейная регрессия
![]() согласуется со статистическими данными,
найдем (с надежностью=0,95
) доверительные интервалы для параметров
согласуется со статистическими данными,
найдем (с надежностью=0,95
) доверительные интервалы для параметров
![]() и
и![]() линейной регрессии. Для нахождения
доверительных интервалов применим
известные формулы:
линейной регрессии. Для нахождения
доверительных интервалов применим
известные формулы:
![]() ,
,
где
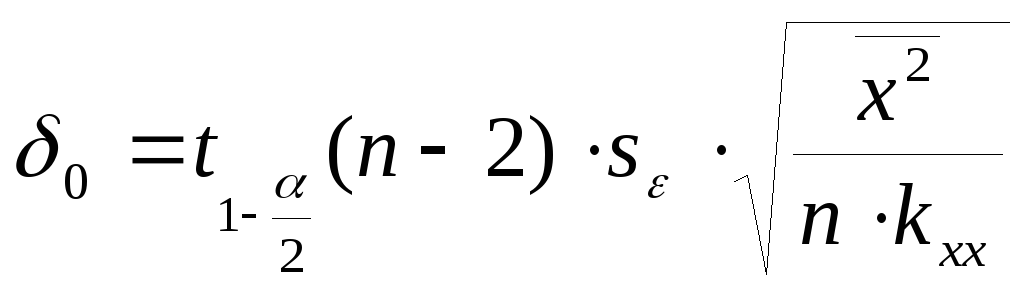 ,
,![]() - квантиль распределения Стьюдента
порядка
- квантиль распределения Стьюдента
порядка![]() сk=n-2
степенями свободы,
сk=n-2
степенями свободы,
![]() ;
;
![]() ,
где
,
где
![]() .
.
В
данном случае
![]() =
=![]() ,
,![]() ;
;

![]() ;
;
![]() =
=![]() .
.
Применив приведенные выше формулы для доверительных интервалов, окончательно получим
![]() ,
,
![]() .
.
Задача 5.
Предположим, что
в педагогическом эксперименте участвовали
три группы студентов по 10 человек в
каждой. В группах применили различные
методы обучения: в первой – традиционный
![]() ,
во второй – основанный на компьютерных
технологиях
,
во второй – основанный на компьютерных
технологиях![]() ,
в третьей – метод, широко использующий
задания для самостоятельной работы
,
в третьей – метод, широко использующий
задания для самостоятельной работы![]() .
Знания оценивались по десятибалльной
системе.
.
Знания оценивались по десятибалльной
системе.
Требуется обработать
полученные данные об экзаменах и сделать
заключение о том, значимо ли влияние
метода преподавания, приняв за уровень
значимости
![]() .
.
Результаты экзаменов
заданы таблицей,
![]() – уровень фактора
– уровень фактора![]() – оценка
– оценка![]() -го
учащегося обучающегося по методике
-го
учащегося обучающегося по методике![]() .
.
5.0.
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Уровень фактора
|
|
6 |
7 |
9 |
4 |
6 |
7 |
5 |
4 |
6 |
5 |
|
|
10 |
9 |
10 |
7 |
9 |
8 |
10 |
8 |
5 |
6 | |
|
|
8 |
7 |
9 |
5 |
9 |
7 |
5 |
6 |
7 |
6 |
Поместим в таблице
экзаменационные оценки (![]() ),
их отклонения от общей средней (
),
их отклонения от общей средней (![]() )
и квадраты этих отклонений
)
и квадраты этих отклонений![]() .
Уровни фактора означают:
.
Уровни фактора означают:![]() - традиционный метод,
- традиционный метод,![]() - применение компьютерной технологии,
- применение компьютерной технологии,![]() - увеличение доли самостоятельной
работы.
- увеличение доли самостоятельной
работы.
|
Номер испытан.1 |
Уровни
фактора
| ||||||||
|
|
|
| |||||||
|
Оценки
|
|
|
Оценки
|
|
|
Оценки
|
|
| |
|
1 |
6 |
-1 |
1 |
10 |
3 |
9 |
8 |
1 |
1 |
|
2 |
7 |
0 |
0 |
9 |
2 |
4 |
7 |
0 |
0 |
|
3 |
9 |
2 |
4 |
10 |
3 |
9 |
9 |
2 |
4 |
|
4 |
4 |
-3 |
9 |
7 |
0 |
0 |
5 |
-2 |
4 |
|
5 |
6 |
-1 |
1 |
9 |
2 |
4 |
9 |
2 |
4 |
|
6 |
7 |
0 |
0 |
8 |
1 |
1 |
7 |
0 |
0 |
|
7 |
5 |
-2 |
4 |
10 |
3 |
9 |
5 |
-2 |
4 |
|
8 |
4 |
-3 |
9 |
8 |
1 |
1 |
6 |
-1 |
1 |
|
9 |
6 |
-1 |
1 |
5 |
-2 |
4 |
7 |
0 |
0 |
|
10 |
5 |
-2 |
4 |
6 |
-1 |
1 |
6 |
-1 |
1 |
|
Груп. сред.2 |
5,9 |
|
|
8,2 |
|
|
6,9 |
|
|
|
|
|
33 |
|
42 |
|
19 | |||
1 Номер испытания (порядковый номер студента группы).
2 Групповая средняя (средний балл группы).
Общая средняя равна
![]() .
.
![]() ;
;
![]() .
.
![]() .
.
В нашем примере p=3 (p - количество факторов), q=10 (q - количество студентов), поэтому для степеней свободы получаются следующие значения: pq-1=29, p-1=2, p(q-1)=27.
Находим
выборочные дисперсии:
![]() ;
;
![]() ;
;
![]() .
.
Примем в качестве нулевой гипотезу о том, что выявленное различие групповых средних (средних баллов) случайно, т.е. при уровне значимости =0,05 средние баллы совпадают.
Для
проверки этой гипотезы следует
воспользоваться F-критерием
Фишера-Снедекора. Вычисляется
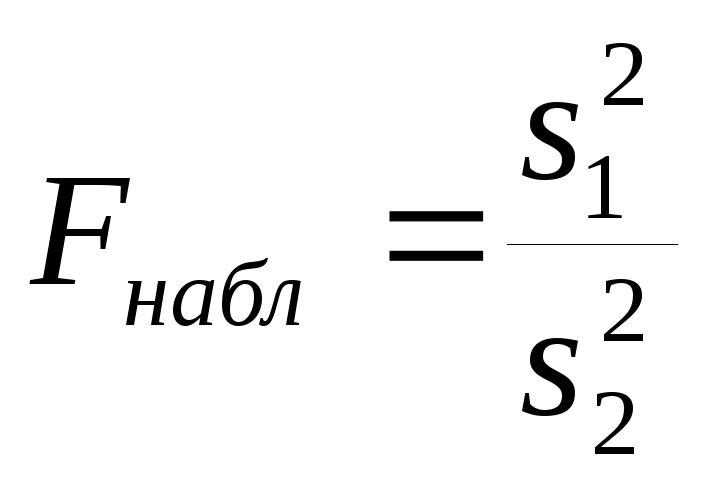 .
.
По
таблицам находится критическая точка
![]() .
Здесь
- уровень значимости,
.
Здесь
- уровень значимости,
![]() - число степеней свободы для дисперсии
- число степеней свободы для дисперсии![]() (в
числитель формулы вписывается большая
из дисперсий),
(в
числитель формулы вписывается большая
из дисперсий),![]() - число степеней свободы для меньшей
дисперсии
- число степеней свободы для меньшей
дисперсии![]() .
В случае
.
В случае![]() нулевая гипотеза принимается, в случае
нулевая гипотеза принимается, в случае![]() она отвергается.
она отвергается.
В
примере
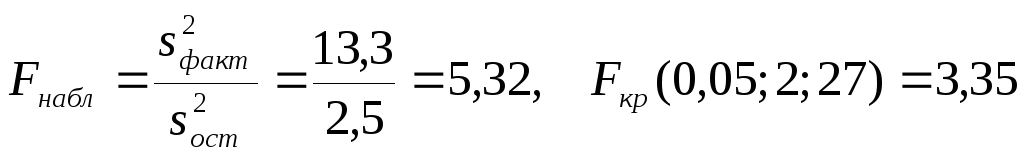 .
.
Таким
образом, нулевая гипотеза отвергается,
и следует считать, что средние баллы
групп различаются "значимо". В
частности, повышение качества знаний
под воздействием уровня
![]() фактораF
нельзя считать случайным.
фактораF
нельзя считать случайным.
Задача 6.
Группировка статистических данных.
По промышленным предприятиям города имеются следующие данные за отчетный год:
|
№ |
Объем продукции, млн. руб. |
Среднегодовая стоимость основных средств, млн. руб. |
Среднесписочное число работников, чел. |
Прибыль, млн. руб. |
|
1 |
478,0 |
19,1 |
1415 |
112,2 |
|
2 |
207,3 |
9,6 |
813 |
30,2 |
|
3 |
194,4 |
8,9 |
852 |
30,4 |
|
4 |
462,3 |
18,3 |
1409 |
97,3 |
|
5 |
207,1 |
10,1 |
896 |
33,2 |
|
б |
196,5 |
10,0 |
900 |
13,4 |
|
7 |
290,2 |
13,5 |
1195 |
49,3 |
|
8 |
356,6 |
14,0 |
1284 |
62,8 |
|
9 |
422,3 |
17,4 |
1359 |
104,6 |
|
10 |
590,0 |
22,7 |
1490 |
134,6 |
|
11 |
581,0 |
21,8 |
1392 |
138,9 |
|
12 |
297,3 |
12,8 |
1202 |
44,5 |
|
13 |
462,4 |
19,5 |
1378 |
111,6 |
|
14 |
582,3 |
22,1 |
1482 |
143,2 |
Требуется выполнить группировку предприятий по объему продукции, приняв следующие интервалы:
1)до 200 млн. руб.; 2) от 200 до 400 млн.руб.; 3) от 400 млн.руб. и более. По каждой группе и в целом по всем предприятиям определить:
число предприятий;
среднесписочное число работников;
среднегодовую стоимость основных средств;
объем продукции всего; средний объем продукции на одного работника; средний объем продукции на 1 млн. руб. стоимости основных средств;
прибыль всего; среднюю прибыль на одного работника; среднюю прибыль на 1 млн. руб. стоимости основных средств.
Сделать вывод.
Для удобства вычислений заполняем сначала вспомогательную таблицу.
|
Группы предприятий по объему продукции млн. руб. |
Объем продукции, млн. руб. |
Среднегодовая стоимость основных средств, млн. руб. |
Среднесписочное число работников, чел. |
Прибыль, млн. руб. |
|
до 200 |
194,4; 196,5; |
8,9; 10,0; |
852; 900; |
30,4; 13,4; |
|
от 200 до 400 |
207,3; 207,1; 290,2; 356,6; 297,3; |
9,6; 10,1; 13,5; 14,0;12,8; |
813;896; 1195; 1284; 1202; |
30,2; 33,2; 49,3; 62,8; 44,5; |
|
более 400 |
478,0; 462,3; 422,3; 590,0; 581,0; 462,4; 582,3; |
19,1; 18,3; 17,4; 22,7; 21,8; 19,5; 22,1; |
1415; 1409; 1359; 1490; 1392; 1378; 1482; |
112,2; 97,3; 104,6; 134,6; 138,9; 111,6; 143,2; |
Результаты группировки приведены в следующей аналитической таблице.
|
Группы предприятий по объему продукции млн. руб. |
Число предприятий в группе |
Среднесписочное число работников, чел. |
Среднегодовая стоимость основных средств млн. руб. |
Объем продукции |
Прибыль | ||||
|
Всего млн. руб. |
В среднем на 1-го работника тыс. руб. |
В среднем на 1 млн. руб. основных средств |
Всего млн. руб. |
В среднем на 1-го работника тыс. руб. |
В среднем на 1 млн. руб. основных средств | ||||
|
до 200 |
2 |
1752 |
18,9 |
390,9 |
223,1 |
20,68 |
43,8 |
25,0 |
2,317 |
|
от 200 до 400 |
5 |
5390 |
60,0 |
1358,5 |
252,04 |
22,64 |
220 |
40,82 |
3,67 |
|
более 400 |
7 |
9925 |
140,9 |
3578,3 |
360,53 |
25,40 |
842,4 |
84,88 |
5,98 |
|
Итого по всем группам |
14 |
17067 |
219,8 |
5327,7 |
312,16 |
24,24 |
1106,2 |
64,82 |
5,03 |
Значения показателей объема продукции, прибыли, среднегодовой стоимости основных средств и среднесписочного числа работников по каждой группе и по всем предприятиям получаются суммированием соответствующих значений по каждому предприятию из вспомогательной таблицы.
Средние показатели объема продукции и прибыли на одного работника рассчитаны делением соответствующих суммарных показателей на число работников по группе (или по всем предприятиям). Аналогично рассчитаны средние показатели объема продукции и прибыли на один млн. руб. основных средств.
По результатам группировки, приведенной в аналитической таблице, можно сделать следующие выводы.
По объему продукции предприятия разделены на мелкие, средние и крупные. Доля мелких предприятий значительно ниже, чем доля средних и крупных.
Значение объема продукции в среднем на одного работника возрастает от мелких предприятий к крупным (I гр. - 223,1 тыс. руб., II гр. - 252,04 тыс. руб., III гр. - 360,53 тыс.руб.).
Еще более значительно растет прибыль на одного работника (I гр. - 25 тыс. руб., II гр. - 40,82 тыс. руб., III гр. - 84,88 тыс. руб.). На крупных предприятиях прибыль на одного работника в 3,4 раза выше, чем на мелких, и в два с лишним раза выше, чем на средних.
Аналогичная картина наблюдается и при сравнении объема продукции и прибыли в среднем на 1 млн. руб. основных средств. Так для крупных предприятий эта прибыль примерно в два с половиной (5,98:2,317ss2,58) раза больше, чем для мелких и в 1,6 раза больше, чем для средних.
Эти данные свидетельствуют о наибольшей эффективности предприятий третьей группы.
Задача 7.
Абсолютные, относительные и средние величины
По каждому из трех предприятий фирмы (г- порядковый номер предприятия), имеются соответствующие данные о фактическом объеме реализованной в 2000 г. продукции (у0 млн.руб.), о плановом задании по росту реализованной продукции на 2001 г. (8, %), а также о фактическом объеме реализованной в 2001 г. продукции (ух млн.руб.). Статистические данные приведены в таблице.
Требуется определить в целом по фирме:
1) размер планового задания по росту объема реализованной продукции в 2001 г;
2) процент выполнения плана по объему реализованной продукции в 2001г.;
3) показатель динамики реализованной продукции.
|
i |
y0i |
δi% |
y1i |
|
1 |
28,5 |
103,0 |
31 |
|
2 |
51,5 |
105,0 |
55,5 |
|
3 |
62,5 |
102,5 |
63,0 |
При решении задачи используются следующие понятия: Относительный показатель динамики (ОПД) характеризует изменение явления во времени
ОПД=![]() или
в процентах
ОПД=
или
в процентах
ОПД=![]() 100%,
100%,
где
у0
- базовый
уровень исследуемого явления. В нашей
задаче это объем реализованной
продукции в 2000г; уi
(i
-
0,1,2,3,...) - уровень явления за одинаковые
последовательные периоды времени
(например, выпуск продукции по годам).
ОПД иначе называются темпами роста. Они
могут быть базовыми
![]() или цепными
или цепными![]() .
.
Относительный показатель плана ОПВП) - отношение величины показателя по плану (упл) к его фактической величине в базисном (или предшествующем) периоде.
ОПП=![]() или ОПП=
или ОПП=![]() 100%.
100%.
Относительный
показатель выполнения плана (ОПВП) -
отношение фактической
(отчетной) величины показателя у1
к
запланированной на тот же период
времени его величине
![]()
ОПВП=![]()
ОПД,
ОПП и ОПВП связаны соотношением
![]() или
или
опп·опвп=опд.
Решение задачи 7.
1. Найдем размер планового задания в целом по фирме по росту объема реализованной продукции в 2001 г., т.е. ОППф - относительный показатель плана фирмы.
Для
этого найдем сначала плановое задание
на 2001 г. по каждому предприятию
![]() и
в целом по фирме
и
в целом по фирме
![]()
![]() 28,5·1,03+51,5·1,05+62,5·1,025=
28,5·1,03+51,5·1,05+62,5·1,025=
= 29,355 + 54,075 + 64,0625 = 147,4925 (млн.руб.).
Достигнутый
в базисном периоде (2000г.) уровень в целом
по фирме
![]()
составляет
![]() 28,5
+ 51,5 + 62,5 = 142,5 (млн.руб.)
28,5
+ 51,5 + 62,5 = 142,5 (млн.руб.)
Теперь можно найти относительный показатель плана в целом по фирме на 2001г.
ОППф=![]()
или
в процентах ≈103,5%.
2.
Найдем процент выполнения плана по
объему реализованной продукции в 2001 г.
в целом по фирме (ОПВПф). Для этого найдем
фактический уровень, достигнутый в 2001
г.
![]()
![]() 31
+ 55,5 + 63,0 = 149,5 млн.руб., тогда
31
+ 55,5 + 63,0 = 149,5 млн.руб., тогда
ОПВПф=![]() 1,0136108
или 101,36%,
т.е.
план перевыполнен на 1,36%.
1,0136108
или 101,36%,
т.е.
план перевыполнен на 1,36%.
3. Найдем относительный показатель динамики реализованной продукции в целом по фирме (ОПДф)
ОПДф=![]() 1,0491228
или ≈104,91%,
1,0491228
или ≈104,91%,
т.е. фактический рост составил ≈4,91%.
Проверка: ОПДф=ОППф·ОПВПф=1,035035·1,0136108=1,049123.
Задача 8.
Элементы дисперсионного анализа.
По
каждой из трех основных рабочих профессий
цеха (i
-порядковый номер профессии: 1-токари;
2-фрезеровщики; 3-слесари) имеются
соответствующие данные о числе
рабочих профессии (![]() чел.), о средней заработной плате
чел.), о средней заработной плате
(![]() руб.), а также о внутригрупповой дисперсии
заработной платы (
руб.), а также о внутригрупповой дисперсии
заработной платы (![]() руб2).
Статистические
данные за месяц приведены в таблице.
руб2).
Статистические
данные за месяц приведены в таблице.
Требуется:
определить общую дисперсию заработной платы рабочих цеха;
оценить однородность совокупности рабочих цеха по уровню месячной заработной платы;
определить, на сколько процентов дисперсия в размере заработной платы обусловлена различиями в профессии рабочих и влиянием других причин.
|
i |
|
|
|
|
1 |
52 |
2650 |
2400 |
|
2 |
26 |
2780 |
3100 |
|
3 |
42 |
2420 |
730 |
Предварительные сведения.
Для
характеристики величины вариации
(колеблемости) признака статистической
совокупности используются абсолютные
и относительные показатели.
В качестве абсолютных показателей чаще
всего рассматривают дисперсию
![]() и
среднеквадратическое отклонение
и
среднеквадратическое отклонение
![]() (СКО)
(СКО)
![]() ,
,
где
![]() -
наблюдённые значения признака (варианты),п
-
общее число вариант (объем
выборки). Суммирование в этой формуле
производится по всем вариантам;
-
наблюдённые значения признака (варианты),п
-
общее число вариант (объем
выборки). Суммирование в этой формуле
производится по всем вариантам;
![]() -
среднее значение признака,
-
среднее значение признака,
![]() - среднее
значение квадрата признака
- среднее
значение квадрата признака
![]() .
.
Изучая
только общую дисперсию интересующего
исследователя признака, нельзя
оценить влияние отдельных факторов,
как качественных, так и количественных,
на величину признака. Это можно сделать
при помощи метода группировки, когда
варианты
![]() подразделяются
на непересекающиеся группы по
признаку-фактору.
При этом, кроме общей средней
подразделяются
на непересекающиеся группы по
признаку-фактору.
При этом, кроме общей средней
![]() по
всей выборке, рассматриваются
средние по отдельным группам
по
всей выборке, рассматриваются
средние по отдельным группам
![]() и следующие показатели дисперсии:
и следующие показатели дисперсии:
общая дисперсия
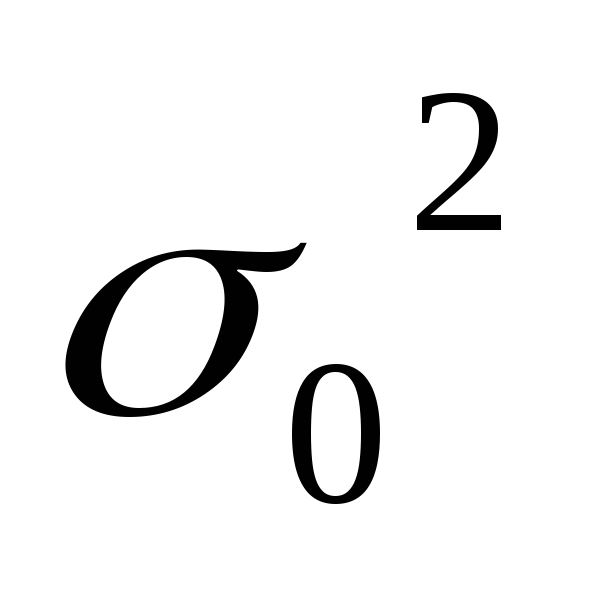
межгрупповая дисперсия
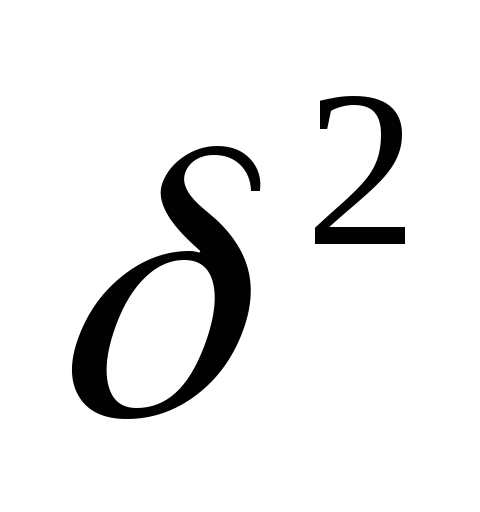 ,
,внутригрупповые дисперсии
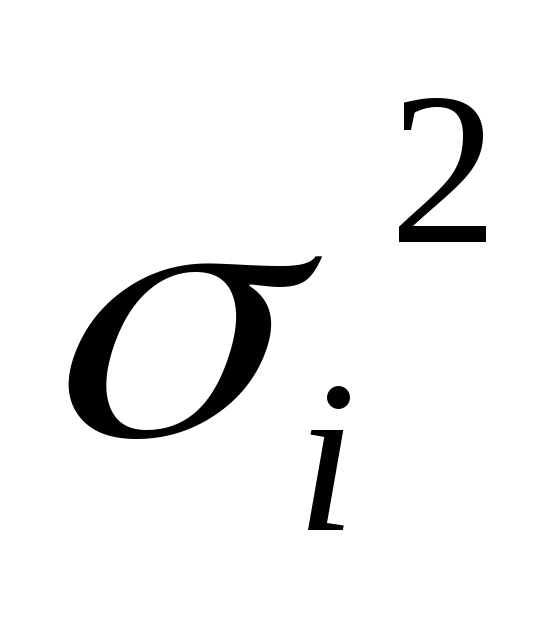 ,
,средняя внутригрупповая дисперсия
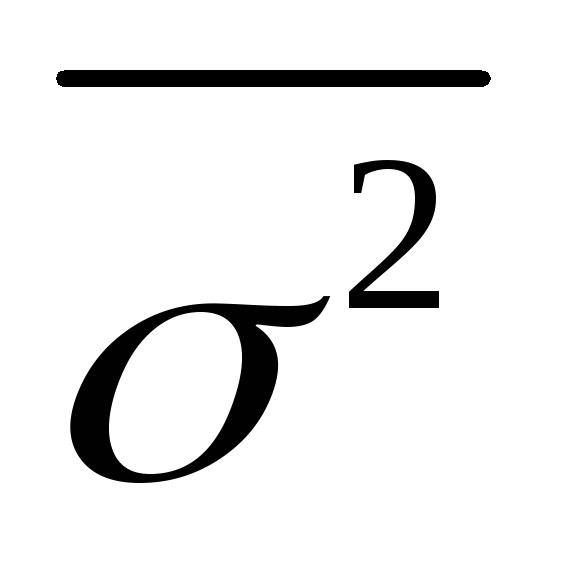 .
Кратко
охарактеризуем эти дисперсии.
.
Кратко
охарактеризуем эти дисперсии.
1.
Общая дисперсия
![]() учитывает
влияние всех факторов, от которых
зависит величина изучаемого признака
X
учитывает
влияние всех факторов, от которых
зависит величина изучаемого признака
X
![]() ,
,
где
![]() -
общая
средняя по всей выборке.
-
общая
средняя по всей выборке.
2.
Межгрупповая дисперсия
![]() (дисперсия групповых средних) отражаетсистематическую
вариацию, т.е. те различия в величине
изучаемого признака, которые
возникают под влиянием фактора,
положенного в основу группировки. Эта
дисперсия определяется по формуле:
(дисперсия групповых средних) отражаетсистематическую
вариацию, т.е. те различия в величине
изучаемого признака, которые
возникают под влиянием фактора,
положенного в основу группировки. Эта
дисперсия определяется по формуле:
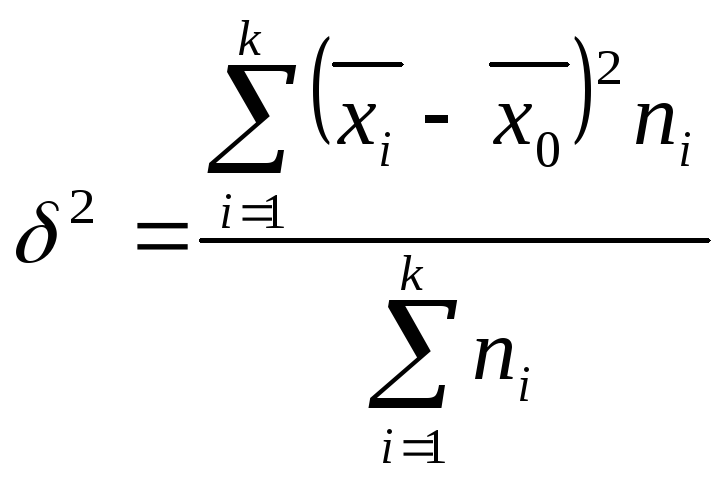
здесь
![]() - внутригрупповые
средние,
- внутригрупповые
средние,
![]() - число вариант вi
-ой
группе; к
число
групп, суммирование производится по
различным группам.
- число вариант вi
-ой
группе; к
число
групп, суммирование производится по
различным группам.
3. Внутригрупповая дисперсия
![]()
отражает
рассеяние значений
![]() признака,
относящихся к одному уровню группировочного
фактора, поэтому она определяется не
этим фактором, а другими
причинами.
признака,
относящихся к одному уровню группировочного
фактора, поэтому она определяется не
этим фактором, а другими
причинами.
4.
Средняя внутригрупповая дисперсия
![]() ,
так
же как и
,
так
же как и
![]() , характеризует
случайную вариацию, возникающую под
влиянием других, неучтенных факторов,
и не зависит от условия, положенного в
основу группировки. Эта дисперсия
определяется по формуле
, характеризует
случайную вариацию, возникающую под
влиянием других, неучтенных факторов,
и не зависит от условия, положенного в
основу группировки. Эта дисперсия
определяется по формуле
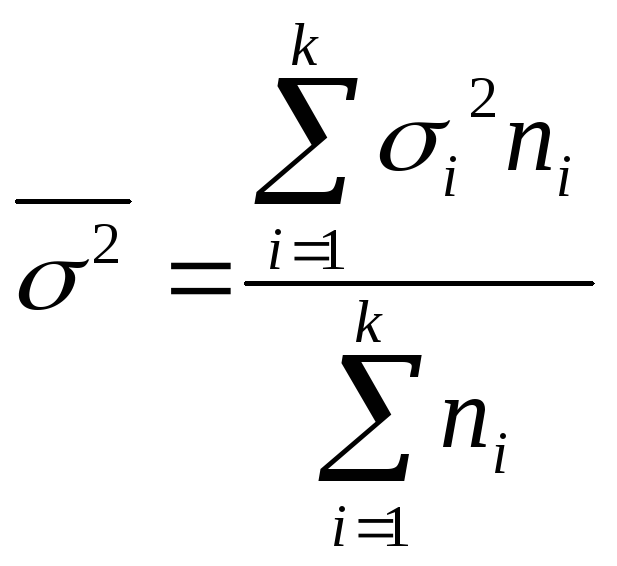 .
.
Можно доказать, что имеет место правило сложения дисперсий
![]()
Отношение
![]() показывает, какую долю общей дисперсии
составляет
показывает, какую долю общей дисперсии
составляет
дисперсия, возникающая под влиянием группировочного фактора, т.е. позволяет оценить влияние этого фактора на величину изучаемого признака X.
При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в разных совокупностях используются относительные показатели вариации. Наиболее распространенным среди относительных показателей вариации является коэффициент вариации
![]()
Его применяют также и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Решение задачи 8.
1. Найдем среднюю из внутригрупповых дисперсий
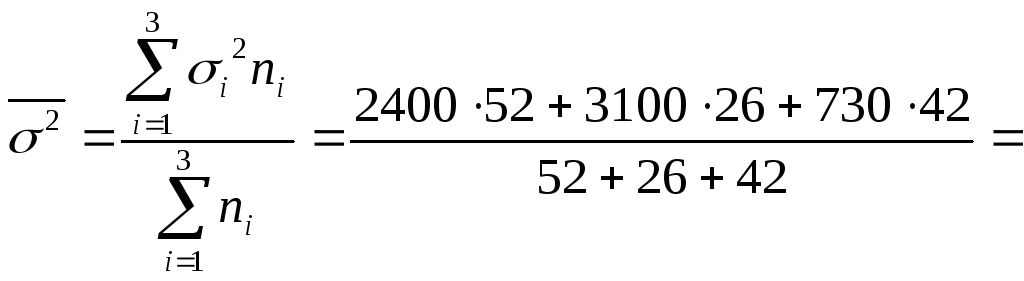 1967,17
(руб2).
1967,17
(руб2).
Определим среднюю зарплату по цеху для основных рабочих профессий (общую среднюю)
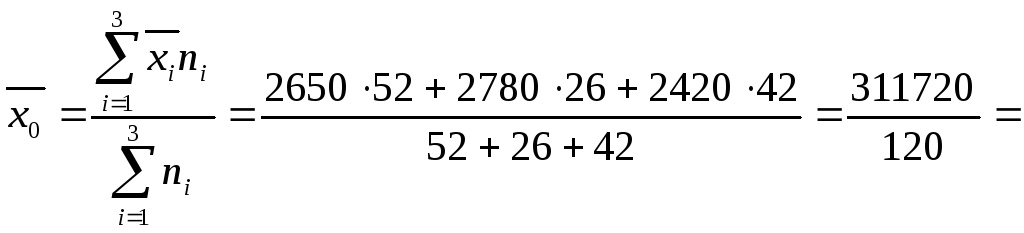 2597,67(руб).
2597,67(руб).
Находим межгрупповую дисперсию
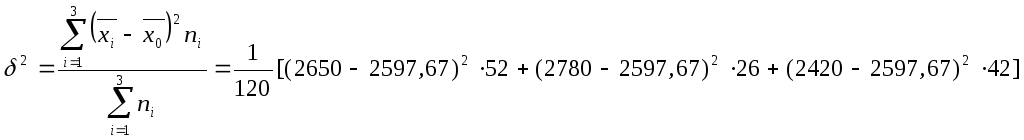 =19438(руб2).
=19438(руб2).
Используя правило сложения дисперсий, найдем общую дисперсию заработной платы:
![]() =
19438
+1967 = 21405 (руб2).
=
19438
+1967 = 21405 (руб2).
2. Оценим однородность совокупности рабочих цеха по уровню месячной заработной платы с помощью коэффициента вариации
![]() 5,63%.
Так
как V
< 33
%, то совокупность считается однородной.
5,63%.
Так
как V
< 33
%, то совокупность считается однородной.
3. Общая дисперсия заработной платы рабочих цеха обусловлена различиями в профессии на
![]() .
.
Эта же дисперсия обусловлена влиянием других причин на
![]()
Задача 9.
Элементы корреляционного анализа.
По 14-ти предприятиям городского хозяйства (i-порядковый номер предприятия) имеются соответствующие данные об объеме продукции (услуг) за месяц (у млн.руб.) и уровне механизации труда (х, %). Статистические данные
приведены в таблице.
Для выявления наличия корреляционной связи между объемом продукции
и уровнем механизации труда требуется:
1) измерить тесноту связи между признаками с помощью коэффициента
корреляции рангов Спирмена;
проверить его достоверность на уровне значимости α= 0,05;
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
98 |
89 |
109 |
110 |
91 |
90 |
65 |
99 |
105 |
101 |
91 |
90 |
77 |
90 |
|
|
94 |
63 |
92 |
63 |
98 |
99 |
95 |
69 |
84 |
89 |
99 |
97 |
94 |
98 |
С
помощью выборочного коэффициента
ранговой корреляции Спирмена
![]() оценивается
теснота связи между двумя качественными
переменными X
и
Y.
Этот
коэффициент применяется и в случае
количественных переменных, если
заранее не гарантируется нормальность
распределения двумерной случайной
величины
(X,Y).
оценивается
теснота связи между двумя качественными
переменными X
и
Y.
Этот
коэффициент применяется и в случае
количественных переменных, если
заранее не гарантируется нормальность
распределения двумерной случайной
величины
(X,Y).
Выборочный
коэффициент
![]() служит
точечной оценкой генерального
коэффициента
ранговой корреляции
служит
точечной оценкой генерального
коэффициента
ранговой корреляции
![]() .
Коэффициенты
.
Коэффициенты
![]() и
и
![]() изменяются
от минус единицы до плюс единицы. Чем
ближе
изменяются
от минус единицы до плюс единицы. Чем
ближе
![]() к
1, тем теснее связь между переменными X
и
Y.
к
1, тем теснее связь между переменными X
и
Y.
1.
Для того чтобы вычислить коэффициент
ранговой корреляции
![]() ,
нужно
сначала провести ранжировку объектов
и получить две согласованные
последовательности
рангов.
,
нужно
сначала провести ранжировку объектов
и получить две согласованные
последовательности
рангов.
Расположим наблюдаемые пары в порядке невозрастания качества по показателю X:
|
|
99 |
99 |
98 |
98 |
97 |
95 |
94 |
94 |
92 |
89 |
84 |
69 |
63 |
63 |
|
|
90 |
91 |
91 |
90 |
90 |
65 |
98 |
77 |
109 |
101 |
105 |
99 |
89 |
110 |
Затем пронумеруем объекты (числа) в каждой из строк в порядке неубывания. Рангом объекта называется его номер в ранжировке. Получим следующую таблицу:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
9 |
7 |
8 |
10 |
11 |
14 |
6 |
13 |
2 |
4 |
3 |
5 |
12 |
1 |
В первой ранжировке обведены группы объектов, имеющих одинаковое качество по переменной X; во второй ранжировке единообразно отмечены объекты, имеющие одинаковое качество по переменной Y.
Далее объектам одинакового качества присваиваем средние ранги (средние арифметические порядковых номеров этих объектов). В результате получим две согласованные последовательности рангов:
|
|
1,5 |
1,5 |
3,5 |
3,5 |
5 |
6 |
7,5 |
7,5 |
9 |
10 |
11 |
12 |
13,5 |
14,5 |
|
|
10 |
7,5 |
7,5 |
10 |
10 |
14 |
6 |
13 |
2 |
4 |
3 |
5 |
12 |
1 |
|
|
-8,5 |
-6 |
-4 |
-6,5 |
-5 |
-8 |
1,5 |
-5,5 |
7 |
6 |
8 |
7 |
1,5 |
13,5 |
В
последней строке записаны разности
рангов
![]() .
.
Найдем
сумму квадратов разностей рангов:
![]() =670,5
и по известнойформуле
вычислим выборочный коэффициент ранговой
корреляции Спирмена:
=670,5
и по известнойформуле
вычислим выборочный коэффициент ранговой
корреляции Спирмена:
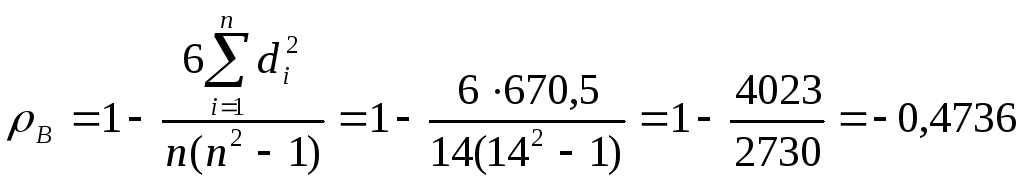
2) Для проверки статистической значимости выборочного коэффициента ранговой корреляции Спирмена на заданном уровне значимости α выдвигается гипотеза Но об отсутствии ранговой корреляционной связи:
![]() .
.
Для проверки выдвинутой гипотезы используется статистика Стьюдента
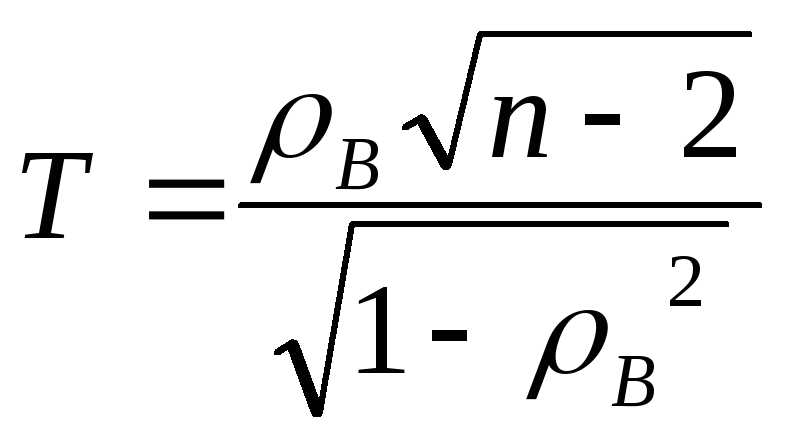 ,
,
где п - число пар (xi, yi) в выборке.
При условии справедливости гипотезы H0 случайная величина Т имеет известное t -распределение Стьюдента с к=п-2 степенями свободы.
Зная
![]() ,
вычисляем
наблюдаемое значение статистики
Стьюдента:
,
вычисляем
наблюдаемое значение статистики
Стьюдента:
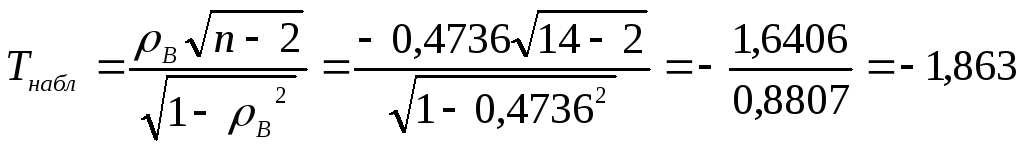
и число степеней свободы к = п - 2 = 12.
По таблице критических точек распределения Стьюдента для двусторонней критической области находим критическую точку статистики Стьюдента (см. например [4]),
![]() .
.
Критерий проверки:
Если
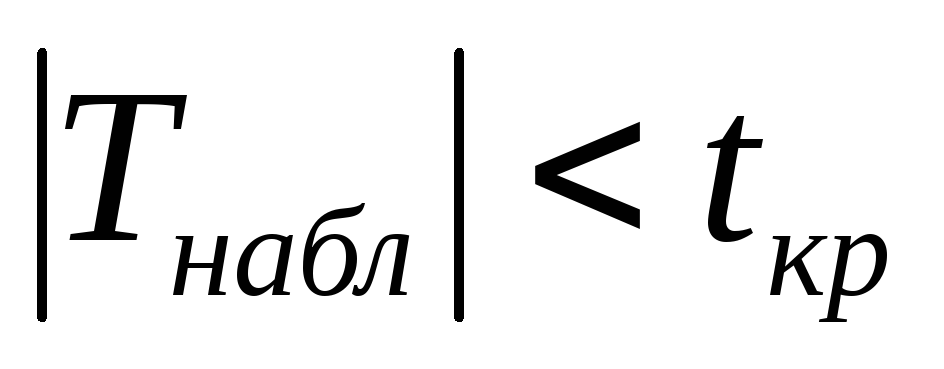 ,
то гипотезаH0
сохраняется
(ранговая корреляционная связь
практически отсутствует);
,
то гипотезаH0
сохраняется
(ранговая корреляционная связь
практически отсутствует);Если
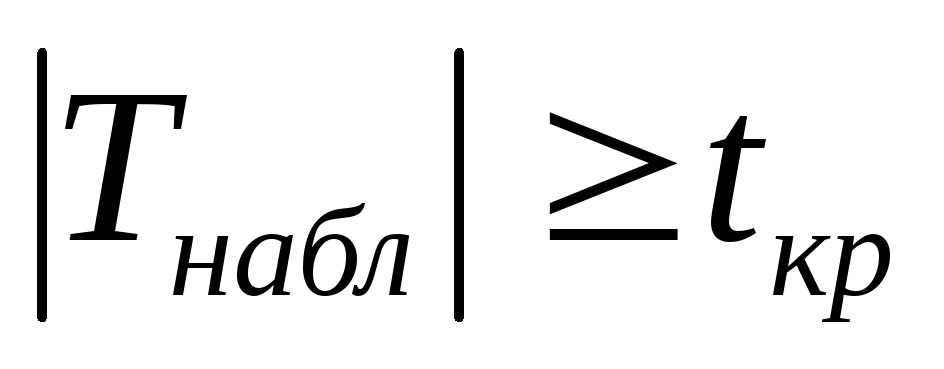 ,
то
гипотеза Н0
отвергается (существует значимая
корреляционная связь между переменными
X
и
Y).
,
то
гипотеза Н0
отвергается (существует значимая
корреляционная связь между переменными
X
и
Y).
В
нашем случае \Тнабл\
= 1,863
<![]() =2,18,
поэтому в соответствие с критерием
проверки заключаем, что
=2,18,
поэтому в соответствие с критерием
проверки заключаем, что
![]() незначимо
отличается от нуля, т.е. ранговая
корреляционная
связь практически отсутствует.
незначимо
отличается от нуля, т.е. ранговая
корреляционная
связь практически отсутствует.
Задача 10.
Прогнозирование на основе сглаженного временного ряда
Динамика удельного расхода условного топлива на производство тепло-энергии (yt, кг/Гкал) на ТЭЦ по годам представлена в таблице. Требуется:
произвести сглаживание ряда методом трехлетней скользящей средней;
выровнять ряд по прямой - т.е. оценить параметры bo,b1 линейного тренда
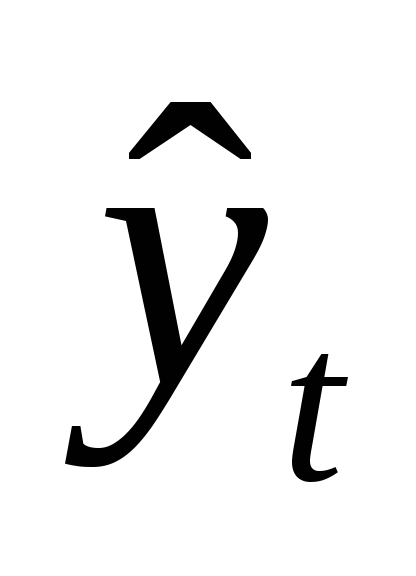 =
b0
+ b1t
методом
наименьших квадратов;
=
b0
+ b1t
методом
наименьших квадратов; начертить графики первичного и сглаженных рядов;
на уровне значимости α = 0,05 проверить согласованность линейной трендовой модели с результатами наблюдений;
методом экстраполяции найти точечные и интервальные (с доверитель ной вероятностью γ = 0,95) оценки прогноза экономического показателя yt на 2002 и 2003г.г.
|
|
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
yt |
169,2 |
168,1 |
168,6 |
168,4 |
167,9 |
167,6 |
167,8 |
166,9 |
167,1 |
(n=9) Временным рядом называется последовательность значений (уровней) некоторого экономического показателя yt, расположенных в порядке возрастания времени. Уровни ряда должны отражать значения экономического показателя за одинаковые или через одинаковые промежутки времени.
Одной из важнейших задач исследования временного ряда является задача выявления основной тенденции развития (тренда) изучаемого процесса.
Решение этой задачи необходимо для прогнозирования. При этом исходят из того, что тенденция развития, установленная в прошлом, может быть распространена (экстраполирована) на будущий период.
Наиболее простыми и часто применяемыми способами выявления основной тенденции развития являются сглаживание временного ряда методом скользящей средней или выравнивание по прямой методом наименьших квадратов.
1) Метод скользящей средней основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени "скользит" вдоль ряда, получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд.
Для нашего примера скользящие средние находим по формуле
![]() .
.
Например, при t = 2
![]() (169,2
+168,1 +168,9)
(169,2
+168,1 +168,9)![]() 168,7,
168,7,
при
t
=
3
![]() (168,1
+168,9 +168,4)
(168,1
+168,9 +168,4)![]() 168,5.
168,5.
По результатам получим сглаженный ряд:
|
|
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
yt |
– |
168,6 |
168,4 |
168,3 |
168,0 |
167,8 |
167,8 |
167,3 |
– |
2)
По статистическим данным найдем оценки
![]() и
и
![]() параметров
линейного тренда
параметров
линейного тренда
![]() методом
наименьших квадратов. Для этого применим
известные формулы [1]:
методом
наименьших квадратов. Для этого применим
известные формулы [1]:
![]() ,
,
где
![]() .
.
Здесь и в дальнейшем t - номер уровня ряда: 1993 г. соответствует номер 1,... 2001 году - номер 9.
Вычисление
средних значений
![]() организуем в форме расчетнойтаблицы.
организуем в форме расчетнойтаблицы.
-

yt
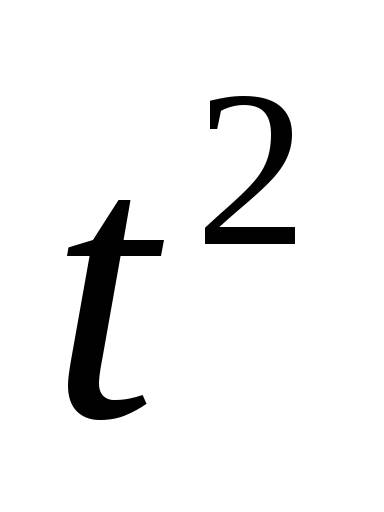
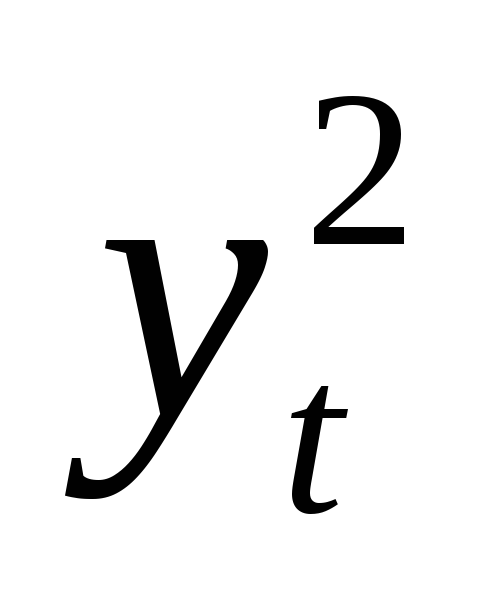
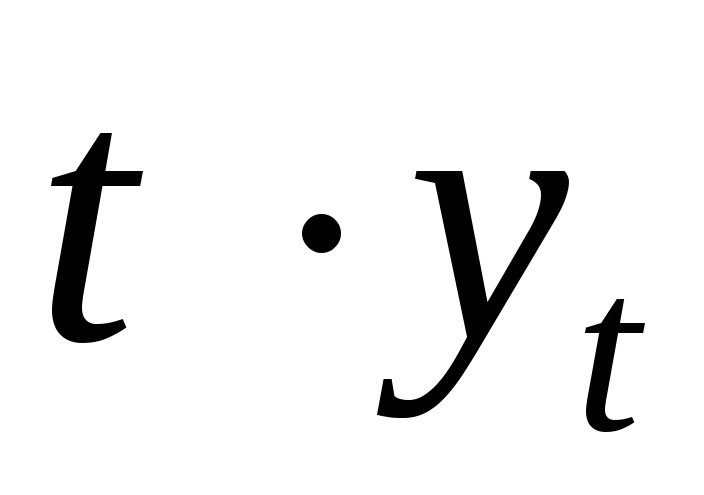
1
169,2
1
28628,64
169,2
2
168,1
4
28257,61
336,2
3
168,6
9
28425,96
505,8
4
168,4
16
28358,56
673,6
5
167,9
25
28190,41
839,5
6
167,6
36
28089,76
1005,6
7
167,8
49
28156,84
1174,6
8
166,9
64
27855,61
1335,2
9
167,1
81
27922,41
1503,9
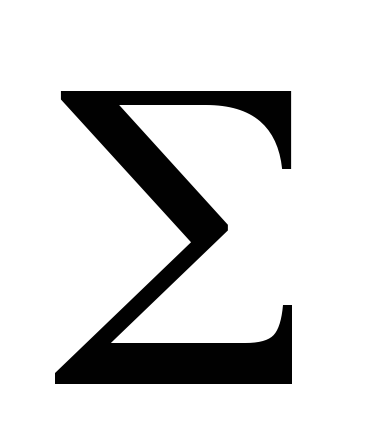
45
1511,6
285
253885,8
7543,6

5
167,955
31,67
28209,53
838,18
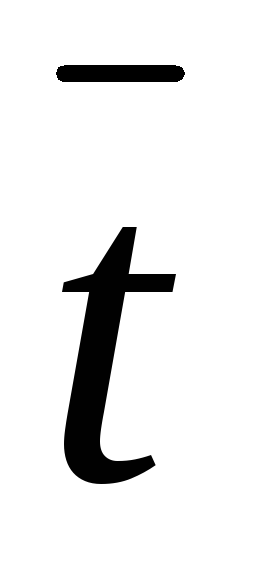
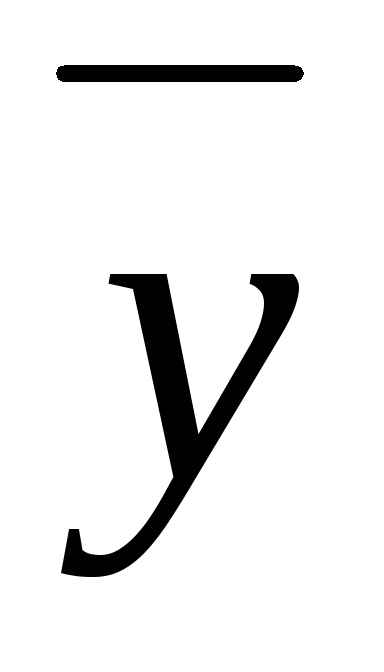
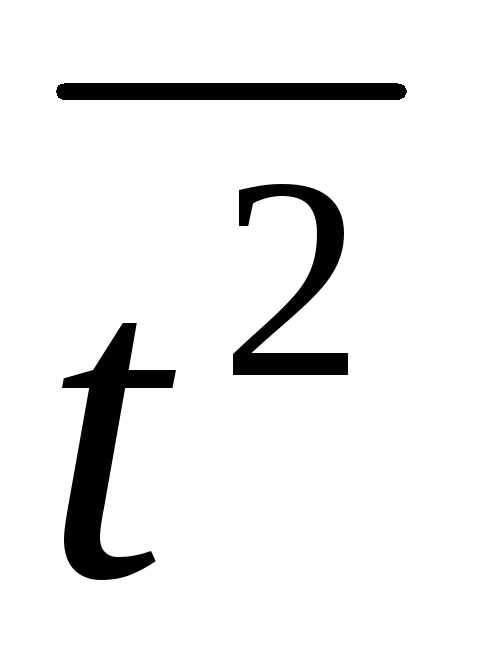
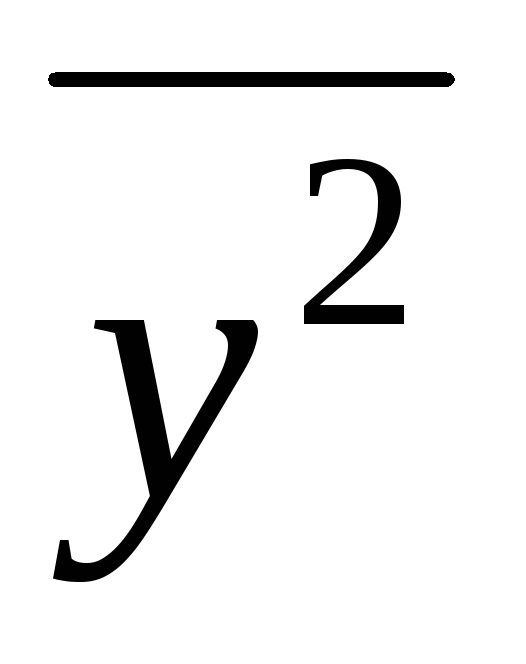
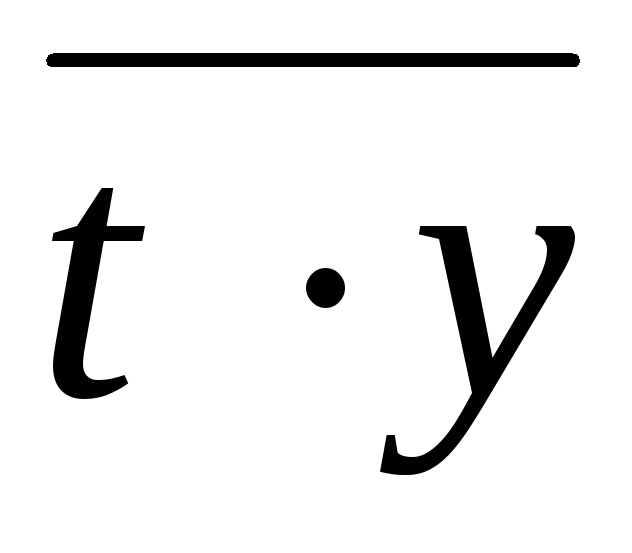
![]()
![]()
![]() .
.
Таким
образом, искомые оценки параметров
линейного аренда равны:
![]() =
169,1695,
=
169,1695,
![]() =
-0,2429. Уравнение линейного тренда имеет
вид:
=
-0,2429. Уравнение линейного тренда имеет
вид:
![]() 169,1695
- 0,2429·t.
169,1695
- 0,2429·t.
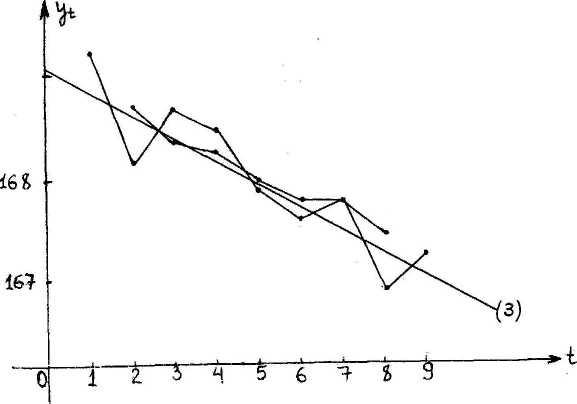 Н
Н
(2)
169
а рисунке цифрой (1) отмечен первичный ряд, цифрой (2) - скользящая трехлетняя средняя, цифрой (3) помечен ряд, выровненный по прямой.
(1)
4
(1)![]() об отсутствии линейной статистической
связи переменных
об отсутствии линейной статистической
связи переменных![]() и t
на заданном уровне значимости α = 0,05.
Для проверки гипотезы используется
коэффициент
детерминации
и t
на заданном уровне значимости α = 0,05.
Для проверки гипотезы используется
коэффициент
детерминации
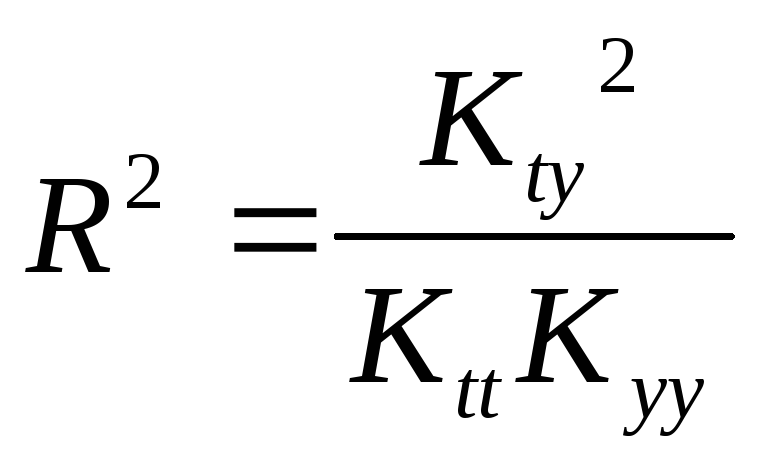 и применяется статистика Фишера
и применяется статистика Фишера![]() с
с
![]() и
к2=п
- 2
степенями
свободы.
и
к2=п
- 2
степенями
свободы.
В
рассматриваемом случае
![]() 28209,53
- (167,955)2
= 0,648,
28209,53
- (167,955)2
= 0,648,
![]() ,
,![]() .
.
Критическое значение статистики Фишера равно
![]() .
.
Так
как
![]() ,
то
выдвинутая гипотеза Hо
отвергается,
что свидетельствует
о согласии линейной трендовой модели
с результатами наблюдений.
,
то
выдвинутая гипотеза Hо
отвергается,
что свидетельствует
о согласии линейной трендовой модели
с результатами наблюдений.
5)
По полученному уравнению линейного
тренда
![]() =169,1695-
0,2429t
найдем
точечные (индивидуальные) прогнозы
показателя
=169,1695-
0,2429t
найдем
точечные (индивидуальные) прогнозы
показателя
![]() на
2002 и 2003 г.г.
на
2002 и 2003 г.г.
Для 2002г. t = 10
![]() 166,7405.
166,7405.
Для 2003г. t = 11
![]() 166,4976.
166,4976.
Дать
интервальную оценку тренда - значит
указать границы интервала, в который
попадет возможное значение переменной
![]() с
заданной доверительной
вероятностью γ
(в
нашем примере γ
=
0,95).
с
заданной доверительной
вероятностью γ
(в
нашем примере γ
=
0,95).
Этот интервал определяется по известным формулам [3]
![]() ,
,
где
δ
-
точность прогноза
![]() ,
здеськ=п-2
-
число степеней свободы, α=1-γ,
,
здеськ=п-2
-
число степеней свободы, α=1-γ,
![]() ищется
по таблице критических
точек распределения Стьюдента для
двусторонней критической области
(см., например [4]); в нашем случае α=1 - 0,95
= 0,05; к
=
9-2 =7;
ищется
по таблице критических
точек распределения Стьюдента для
двусторонней критической области
(см., например [4]); в нашем случае α=1 - 0,95
= 0,05; к
=
9-2 =7;
![]() 2,36.
(Можно воспользоваться так же таблицами
2,36.
(Можно воспользоваться так же таблицами
![]() [3]).
[3]).
![]() -
исправленное среднеквадратическое
отклонение (С.К.О.) индивидуальных
значений зависимой переменной
-
исправленное среднеквадратическое
отклонение (С.К.О.) индивидуальных
значений зависимой переменной![]()
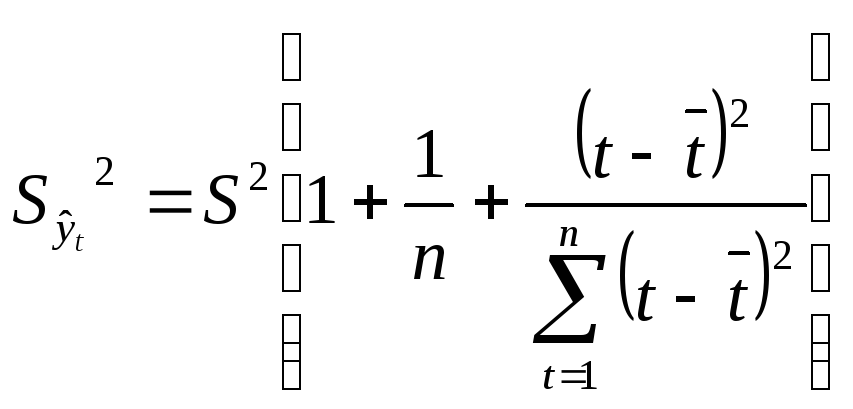 .
.
Из
этой формулы видно, чем больше
![]() ,
тем
меньше точность прогноза. S
- исправленное
С.К.О. ошибок линейной регрессии
,
тем
меньше точность прогноза. S
- исправленное
С.К.О. ошибок линейной регрессии
![]() .
.
Вычисление доверительных интервалов прогнозов организуем в виде таблицы
-
t
yt
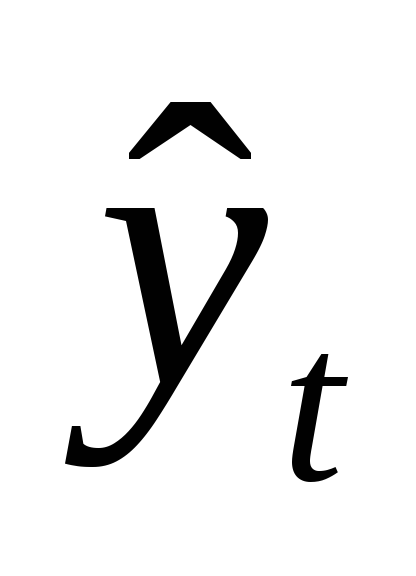
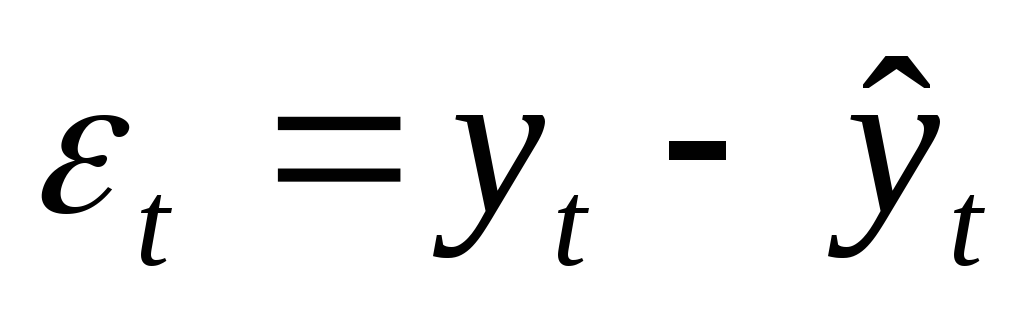
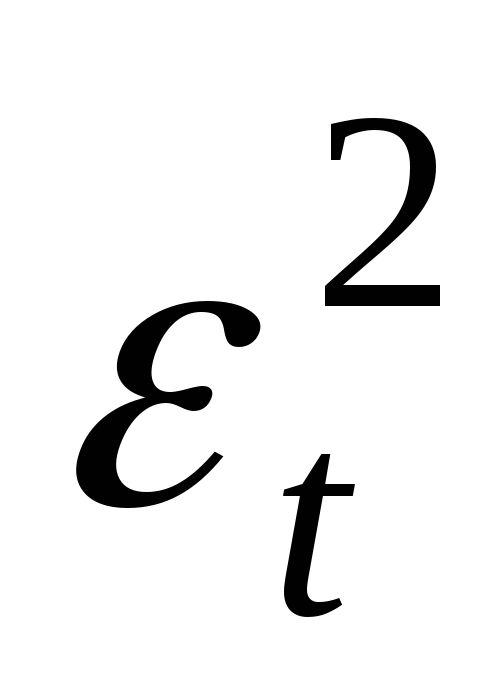
1
169,2
168,9266
0,2734
0,07475
2
168,1
168,6837
-0,5837
0,34071
3
168,6
168,4408
0,1592
0,02534
4
168,4
168,1979
0,2021
0,04084
5
167,9
167,9550
-0,055
0,00303
6
167,6
167,7121
-0,1121
0,01257
7
167,8
167,4692
0,3308
0,10943
8
166,9
167,2263
-0,3263
0,10647
9
167,1
166,9834
0,1166
0,01360

–
–
–
0,72674
![]() .
.
![]() .
.
Дальнейшие вычисления проводим отдельно для t =10 (2002 г.) и t =11 (2003 г.)
Для t = 10
![]() .
.
![]()
![]() ,
,
166,74-0,94<![]() <166,74+0,94.
<166,74+0,94.
Итак, с вероятностью γ = 0,95, удельный расход условного топлива в 2002 г. будет принадлежать интервалу (кг/Гкал)
165,8
<![]() <
167,68.
<
167,68.
Аналогично для 2003 г. t = 11, получим
![]() .
.
![]() ,
,
![]() ,
,
166,498-0,995<![]() <166,498+0,995.
165,50<
<166,498+0,995.
165,50<![]() <167,49,
γ=0,95.
<167,49,
γ=0,95.
Приложение 1
Таблица значений
функции Лапласа
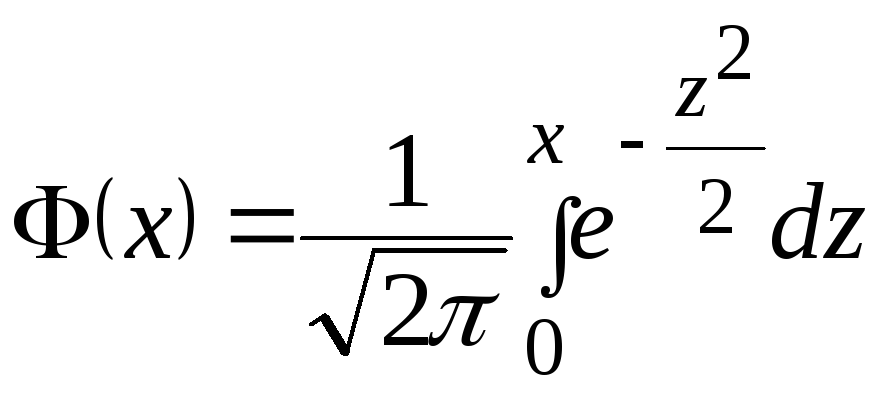
|
|
|
|
|
|
|
|
|
|
0,00 |
0,0000 |
0,32 |
0,1255 |
0,64 |
0,2389 |
0,96 |
0,3315 |
|
0,01 |
0,0040 |
0,33 |
0,1293 |
0,65 |
0,2422 |
0,97 |
0,3340 |
|
0,02 |
0,0080 |
0,34 |
0,1331 |
0,66 |
0,2454 |
0,98 |
0,3365 |
|
0,03 |
0,0120 |
0,35 |
0,1368 |
0,67 |
0,2486 |
0,99 |
0,3389 |
|
0,04 |
0,0160 |
0,36 |
0,1406 |
0,68 |
0,2517 |
1,00 |
0,3413 |
|
0,05 |
0,0199 |
0,37 |
0,1443 |
0,69 |
0,2549 |
1,01 |
0,3438 |
|
0,06 |
0,0239 |
0,38 |
0,1480 |
0,70 |
0,2580 |
1,02 |
0,3461 |
|
0,07 |
0,0279 |
0,39 |
0,1517 |
0,71 |
0,2611 |
1,03 |
0,3485 |
|
0,08 |
0,0319 |
0,40 |
0,1554 |
0,72 |
0,2642 |
1,04 |
0,3508 |
|
0,09 |
0,0359 |
0,41 |
0,1591 |
0,73 |
0,2673 |
1,05 |
0,3531 |
|
0,10 |
0,0398 |
0,42 |
0,1628 |
0,74 |
0,2703 |
1,06 |
0,3554 |
|
0,11 |
0,0438 |
0,43 |
0,1664 |
0,75 |
0,2734 |
1,07 |
0,3577 |
|
0,12 |
0,0478 |
0,44 |
0,1700 |
0,76 |
0,2764 |
1,08 |
0,3599 |
|
0,13 |
0,0517 |
0,45 |
0,1736 |
0,77 |
0,2794 |
1,09 |
0,3621 |
|
0,14 |
0,0557 |
0,46 |
0,1772 |
0,78 |
0,2823 |
1,10 |
0,3643 |
|
0,15 |
0,0596 |
0,47 |
0,1808 |
0,79 |
0,2852 |
1,11 |
0,3665 |
|
0,16 |
0,0636 |
0,48 |
0,1844 |
0,80 |
0,2881 |
1,12 |
0,3686 |
|
0,17 |
0,0675 |
0,49 |
0,1879 |
0,81 |
0,2910 |
1,13 |
0,3708 |
|
0,18 |
0,0714 |
0,50 |
0,1915 |
0,82 |
0,2939 |
1,14 |
0,3729 |
|
0,19 |
0,0753 |
0,51 |
0,1950 |
0,83 |
0,2967 |
1,15 |
0,3749 |
|
0,20 |
0,0793 |
0,52 |
0,1985 |
0,84 |
0,2995 |
1,16 |
0,3770 |
|
0,21 |
0,0832 |
0,53 |
0,2019 |
0,85 |
0,3023 |
1,17 |
0,3790 |
|
0,22 |
0,0871 |
0,54 |
0,2054 |
0,86 |
0,3051 |
1,18 |
0,3810 |
|
0,23 |
0,0910 |
0,55 |
0,2088 |
0,87 |
0,3078 |
1,19 |
0,3830 |
|
0,24 |
0,0948 |
0,56 |
0,2123 |
0,88 |
0,3106 |
1,20 |
0,3849 |
|
0,25 |
0,0987 |
0,57 |
0,2157 |
0,89 |
0,3133 |
1,21 |
0,3869 |
|
0,26 |
0,1026 |
0,58 |
0,2190 |
0,90 |
0,3159 |
1,22 |
0,3883 |
|
0,27 |
0,1064 |
0,59 |
0,2224 |
0,91 |
0,3186 |
1,23 |
0,3907 |
|
0,28 |
0,1103 |
0,60 |
0,2257 |
0,92 |
0,3212 |
1,24 |
0,3925 |
|
0,29 |
0,1141 |
0,61 |
0,2291 |
0,93 |
0,3238 |
1,25 |
0,3944 |
|
0,30 |
0,1179 |
0,62 |
0,2324 |
0,94 |
0,3264 |
|
|
|
0,31 |
0,1217 |
0,63 |
0,2357 |
0,95 |
0,3289 |
|
|
Продолжение приложения 1
|
|
|
|
|
|
|
|
|
|
1,26 |
0,3962 |
1,59 |
0,4441 |
1,92 |
0,4726 |
2,50 |
0,4938 |
|
1,27 |
0,3980 |
1,60 |
0,4452 |
1,93 |
0,4732 |
2,52 |
0,4941 |
|
1,28 |
0,3997 |
1,61 |
0,4463 |
1,94 |
0,4738 |
2,54 |
0,4945 |
|
1,29 |
0,4015 |
1,62 |
0,4474 |
1,95 |
0,4744 |
2,56 |
0,4948 |
|
1,30 |
0,4032 |
1,63 |
0,4484 |
1,96 |
0,4750 |
2,58 |
0,4951 |
|
1,31 |
0,4049 |
1,64 |
0,4495 |
1,97 |
0,4756 |
2,60 |
0,4953 |
|
1,32 |
0,4066 |
1,65 |
0,4505 |
1,98 |
0,4761 |
2,62 |
0,4956 |
|
1,33 |
0,4082 |
1,66 |
0,4515 |
1,99 |
0,4767 |
2,64 |
0,4959 |
|
1,34 |
0,4099 |
1,67 |
0,4525 |
2,00 |
0,4772 |
2,66 |
0,4961 |
|
1,35 |
0,4115 |
1,68 |
0,4535 |
2,02 |
0,4783 |
2,68 |
0,4963 |
|
1,36 |
0,4131 |
1,69 |
0,4545 |
2,04 |
0,4793 |
2,70 |
0,4965 |
|
1,37 |
0,4147 |
1,70 |
0,4554 |
2,06 |
0,4803 |
2,72 |
0,4967 |
|
1,38 |
0,4162 |
1,71 |
0,4564 |
2,08 |
0,4812 |
2,74 |
0,4969 |
|
1,39 |
0,4177 |
1,72 |
0,4573 |
2,10 |
0,4821 |
2,76 |
0,4971 |
|
1,40 |
0,4192 |
1,73 |
0,4582 |
2,12 |
0,4830 |
2,78 |
0,4973 |
|
1,41 |
0,4207 |
1,74 |
0,4591 |
2,14 |
0,4838 |
2,80 |
0,4974 |
|
1,42 |
0,4222 |
1,75 |
0,4599 |
2,16 |
0,4846 |
2,82 |
0,4976 |
|
1,43 |
0,4236 |
1,76 |
0,4608 |
2,18 |
0,4854 |
2,84 |
0,4977 |
|
1,44 |
0,4251 |
1,77 |
0,4616 |
2,20 |
0,4861 |
2,86 |
0,4979 |
|
1,45 |
0,4265 |
1,78 |
0,4625 |
2,22 |
0,4868 |
2,88 |
0,4980 |
|
1,46 |
0,4279 |
1,79 |
0,4633 |
2,24 |
0,4875 |
2,90 |
0,4981 |
|
1,47 |
0,4292 |
1,80 |
0,4641 |
2,26 |
0,4881 |
2,92 |
0,4982 |
|
1,48 |
0,4306 |
1,81 |
0,4649 |
2,28 |
0,4887 |
2,94 |
0,4984 |
|
1,49 |
0,4319 |
1,82 |
0,4656 |
2,30 |
0,4893 |
2,96 |
0,4985 |
|
1,50 |
0,4332 |
1,83 |
0,4664 |
2,32 |
0,4898 |
2,98 |
0,4986 |
|
1,51 |
0,4345 |
1,84 |
0,4671 |
2,34 |
0,4904 |
3,00 |
0,49865 |
|
1,52 |
0,4357 |
1,85 |
0,4678 |
2,36 |
0,4909 |
3,20 |
0,49931 |
|
1,53 |
0,4370 |
1,86 |
0,4686 |
2,38 |
0,4913 |
3,40 |
0,49966 |
|
1,54 |
0,4382 |
1,87 |
0,4693 |
2,40 |
0,4918 |
3,60 |
0,49841 |
|
1,55 |
0,4394 |
1,88 |
0,4699 |
2,42 |
0,4922 |
3,80 |
0,499928 |
|
1,56 |
0,4406 |
1,89 |
0,4706 |
2,44 |
0,4927 |
4,00 |
0,499968 |
|
1,57 |
0,4418 |
1,90 |
0,4713 |
2,46 |
0,4931 |
4,50 |
0,499997 |
|
1,58 |
0,4429 |
1,91 |
0,4719 |
2,48 |
0,4934 |
5,00 |
0,499997 |
Приложение 2
Таблица значений
функции
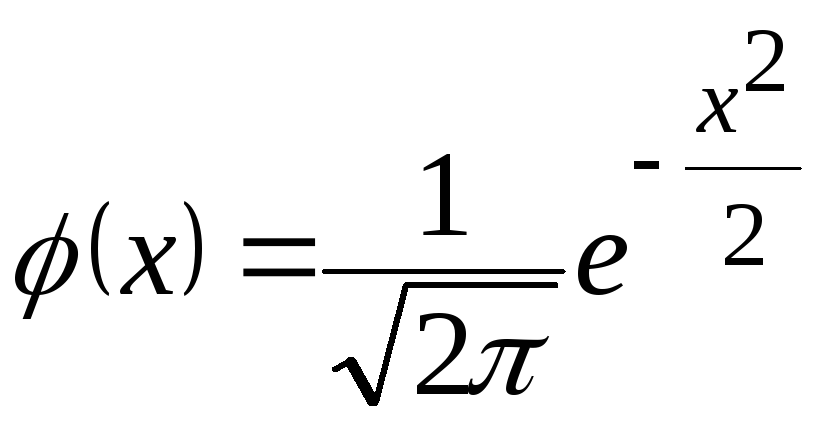
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,0 |
0,399 |
3989 |
3989 |
3988 |
3986 |
3984 |
3982 |
3980 |
3977 |
3973 |
|
0,1 |
3970 |
3965 |
3961 |
3956 |
3951 |
3945 |
3939 |
3932 |
3925 |
3918 |
|
0,2 |
3910 |
3902 |
3894 |
3885 |
3876 |
3867 |
3857 |
3847 |
3836 |
3825 |
|
0,3 |
3814 |
3802 |
3790 |
3778 |
3765 |
3752 |
3739 |
3726 |
3712 |
3697 |
|
0,4 |
3683 |
3668 |
3852 |
3637 |
3621 |
3605 |
3589 |
3572 |
3555 |
3538 |
|
0,5 |
3521 |
3503 |
3485 |
3467 |
3448 |
3429 |
3410 |
3391 |
3372 |
3352 |
|
0,6 |
3332 |
3312 |
3292 |
3271 |
3251 |
3230 |
3209 |
3187 |
3166 |
3144 |
|
0,7 |
3123 |
3101 |
3079 |
3056 |
3034 |
3011 |
2989 |
2966 |
2943 |
2920 |
|
0,8 |
2897 |
2874 |
2850 |
2827 |
2803 |
2780 |
2756 |
2732 |
2709 |
2685 |
|
0,9 |
2661 |
2637 |
2613 |
2589 |
2565 |
2541 |
2516 |
2492 |
2468 |
2444 |
|
1,0 |
0,242 |
2396 |
2371 |
2347 |
2323 |
2299 |
2275 |
2251 |
2227 |
2203 |
|
1,1 |
2179 |
2155 |
2131 |
2107 |
2083 |
2059 |
2036 |
2012 |
1989 |
1965 |
|
1,2 |
1942 |
1919 |
1895 |
1872 |
1849 |
1826 |
1804 |
1781 |
1758 |
1736 |
|
1,3 |
1714 |
1691 |
1669 |
1647 |
1626 |
1604 |
1582 |
1561 |
1539 |
1518 |
|
1,4 |
1497 |
1476 |
1456 |
1435 |
1415 |
1394 |
1374 |
1354 |
1334 |
1315 |
|
1,5 |
1295 |
1276 |
1257 |
1238 |
1219 |
1200 |
1182 |
1163 |
1145 |
1127 |
|
1,6 |
1109 |
1092 |
1074 |
1057 |
1040 |
1023 |
1006 |
0989 |
0973 |
0957 |
|
1,7 |
0940 |
0925 |
0909 |
0893 |
0878 |
0863 |
0848 |
0833 |
0818 |
0804 |
|
1,8 |
0790 |
0775 |
0761 |
0748 |
0734 |
0721 |
0707 |
0694 |
0681 |
0669 |
|
1,9 |
0656 |
0644 |
0632 |
0620 |
0608 |
0596 |
0584 |
0573 |
0562 |
0551 |
|
2,0 |
0,054 |
0529 |
0519 |
0508 |
0498 |
0488 |
0478 |
0468 |
0459 |
0449 |
|
2,1 |
0440 |
0431 |
0422 |
0413 |
0404 |
0396 |
0387 |
0379 |
0371 |
0363 |
|
2,2 |
0355 |
0347 |
0339 |
0332 |
0325 |
0317 |
0310 |
0303 |
0297 |
0290 |
|
2,3 |
0283 |
0277 |
0270 |
0264 |
0258 |
0252 |
0246 |
0241 |
0235 |
0229 |
|
2,4 |
0224 |
0219 |
0213 |
0208 |
0203 |
0198 |
0194 |
0189 |
0184 |
0180 |
|
2,5 |
0175 |
0171 |
0167 |
0163 |
0158 |
0154 |
0151 |
0147 |
0143 |
0139 |
|
2,6 |
0136 |
0132 |
0129 |
0126 |
0122 |
0119 |
0116 |
0113 |
0110 |
0107 |
|
2,7 |
0104 |
0101 |
0099 |
0096 |
0093 |
0091 |
0088 |
0086 |
0084 |
0081 |
|
2,8 |
0079 |
0077 |
0075 |
0073 |
0071 |
0069 |
0067 |
0065 |
0063 |
0061 |
|
2,9 |
0060 |
0058 |
0056 |
0055 |
0053 |
0051 |
0050 |
0048 |
0047 |
0043 |
|
3,0 |
0,004 |
0043 |
0042 |
0040 |
0039 |
0038 |
0037 |
0036 |
0035 |
0034 |
|
3,1 |
0033 |
0032 |
0031 |
0030 |
0029 |
0028 |
0027 |
0026 |
0025 |
0025 |
|
3,2 |
0024 |
0023 |
0022 |
0022 |
0021 |
0020 |
0020 |
0019 |
0018 |
0018 |
|
3,3 |
0017 |
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
0014 |
0013 |
0013 |
|
3,4 |
0012 |
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
0009 |
0009 |
|
3,5 |
0009 |
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
0007 |
0006 |
|
3,6 |
0006 |
0006 |
0006 |
0005 |
0005 |
0005 |
0005 |
0005 |
0005 |
0004 |
|
3,7 |
0004 |
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
0003 |
0003 |
|
3,8 |
0003 |
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
0002 |
0002 |
|
3,9 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0001 |
0001 |
Приложение 3
Критические точки
распределения
![]()
|
Число
степеней свободы
|
Уровень
значимости
| |||||
|
0,01 |
0,025 |
0,05 |
0,95 |
0,975 |
0,99 | |
|
1 |
6,6 |
5,0 |
3,8 |
0,0039 |
0,00098 |
0,00016 |
|
2 |
9,2 |
7,4 |
6,0 |
0,103 |
0,051 |
0,020 |
|
3 |
11,3 |
9,4 |
7,8 |
0,352 |
0,216 |
0,115 |
|
4 |
13,3 |
11,1 |
9,5 |
0,711 |
0,484 |
0,297 |
|
5 |
15,1 |
12,8 |
11,1 |
1,15 |
0,831 |
0,554 |
|
6 |
16,8 |
14,4 |
12,6 |
1,64 |
1,24 |
0,872 |
|
7 |
18,5 |
16,0 |
14,1 |
2,17 |
1,69 |
1,24 |
|
8 |
20,1 |
17,5 |
15,5 |
2,73 |
2,18 |
1,65 |
|
9 |
21,7 |
19,0 |
16,9 |
3,33 |
2,70 |
2,09 |
|
10 |
23,2 |
20,5 |
18,3 |
3,94 |
3,25 |
2,56 |
|
11 |
24,7 |
21,9 |
19,7 |
4,57 |
3,82 |
3,05 |
|
12 |
26,2 |
23,3 |
21,0 |
5,23 |
4,40 |
3,57 |
|
13 |
27,7 |
24,7 |
22,4 |
5,89 |
5,01 |
4,11 |
|
14 |
29,1 |
26,1 |
23,7 |
6,57 |
5,63 |
4,66 |
|
15 |
30,6 |
27,5 |
25,0 |
7,26 |
6,26 |
5,23 |
|
16 |
32,0 |
28,8 |
26,3 |
7,96 |
6,91 |
5,81 |
|
17 |
33,4 |
30,2 |
27,6 |
8,67 |
7,56 |
6,41 |
|
18 |
34,8 |
31,5 |
28,9 |
9,39 |
8,23 |
7,01 |
|
19 |
36,2 |
32,9 |
30,1 |
10,1 |
8,91 |
7,63 |
|
20 |
37,6 |
34,2 |
31,4 |
10,9 |
9,59 |
8,26 |
|
21 |
38,9 |
35,5 |
32,7 |
11,6 |
10,3 |
8,90 |
|
22 |
40,3 |
36,8 |
33,9 |
12,3 |
11,0 |
9,54 |
|
23 |
41,6 |
38,1 |
35,2 |
13,1 |
11,7 |
10,2 |
|
24 |
43,0 |
39,4 |
36,4 |
13,8 |
12,4 |
10,9 |
|
25 |
44,3 |
40,6 |
37,7 |
14,6 |
13,1 |
11,5 |
|
26 |
45,6 |
41,9 |
38,9 |
15,4 |
13,8 |
12,2 |
|
27 |
47,0 |
43,2 |
40,1 |
16,2 |
14,6 |
12,9 |
|
28 |
48,3 |
44,5 |
41,3 |
16,9 |
15,3 |
13,6 |
|
29 |
49,6 |
45,7 |
42,6 |
17,7 |
16,0 |
14,3 |
|
30 |
50,9 |
47,0 |
43,8 |
18,5 |
16,8 |
15,0 |
Приложение 4.
Таблица значений
![]()
|
n |
0,95 |
0,99 |
0,999 |
n |
0,95 |
0,99 |
0,099 |
|
5 |
2,78 |
4,60 |
8,61 |
20 |
2,093 |
2,861 |
3,883 |
|
6 |
2,57 |
4,03 |
6,86 |
25 |
2,064 |
2,797 |
3,745 |
|
7 |
2,45 |
3,71 |
5,96 |
30 |
2,645 |
2,756 |
3,659 |
|
8 |
2,37 |
3,50 |
5,41 |
35 |
2,032 |
2,720 |
3,600 |
|
9 |
2,31 |
3,36 |
5,04 |
40 |
2,023 |
2,708 |
3,558 |
|
10 |
2,26 |
3,25 |
4,78 |
45 |
2,016 |
2.692 |
3,527 |
|
11 |
2,23 |
3,17 |
4,59 |
50 |
2,009 |
2,679 |
3,502 |
|
12 |
2,20 |
3,11 |
4,44 |
60 |
2,001 |
2,662 |
3,464 |
|
13 |
2,18 |
3,06 |
4.32 |
70 |
1,996 |
2,649 |
3,439 |
|
14 |
2,16 |
3,01 |
4,22 |
80 |
1,991 |
2,640 |
3,418 |
|
15 |
2,15 |
2,98 |
4,14 |
90 |
1,987 |
2,633 |
3,403 |
|
16 |
2,13 |
2,95 |
4,07 |
100 |
1,984 |
2,627 |
3,392 |
|
17 |
2,12 |
2,92 |
4,02 |
120 |
1,980 |
2,617 |
3,374 |
|
18 |
2,11 |
2,90 |
3,97 |
|
1,960 |
2,576 |
3,291 |
|
19 |
2,10 |
2,88 |
3,92 |
|
|
|
|
Приложение 5
Таблица значений
![]()

|
n |
0,95 |
0,99 |
0,999 |
n |
0,95 |
0,99 |
0,999 |
|
5 |
1,37 |
2,67 |
5,64 |
20 |
0,37 |
0,58 |
0,88 |
|
6 |
1,09 |
2,01 |
3,88 |
25 |
0,32 |
0,49 |
0,73 |
|
7 |
0,92 |
1,62 |
2,98 |
30 |
0,28 |
0,43 |
0,63 |
|
8 |
0,80 |
1,38 |
2,42 |
35 |
0,26 |
0,38 |
0,56 |
|
9 |
0,71 |
1,20 |
2,06 |
40 |
0,24 |
0,35 |
0,50 |
|
10 |
0,65 |
1,08 |
1,80 |
45 |
0,22 |
0,32 |
0,46 |
|
11 |
0,59 |
0,98 |
1,60 |
50 |
0,21 |
0,30 |
0,43 |
|
12 |
0,55 |
0,90 |
1,45 |
60 |
0,188 |
0,269 |
0,38 |
|
13 |
0,52 |
0,83 |
1,33 |
70 |
0,174 |
0,245 |
0,34 |
|
14 |
0,48 |
0,78 |
1,23 |
80 |
0,161 |
0,226 |
0,31 |
|
15 |
0,46 |
0,73 |
1,15 |
90 |
0,151 |
0,211 |
0,29 |
|
16 |
0,44 |
0,70 |
1,07 |
100 |
0,143 |
0,198 |
0,27 |
|
17 |
0,42 |
0,66 |
1,01 |
150 |
0,115 |
0,160 |
0,211 |
|
18 |
0,40 |
0,63 |
0,96 |
200 |
0,099 |
0,136 |
0,185 |
|
19 |
0,39 |
0,60 |
0,92 |
250 |
0,098 |
0,120 |
0,162 |
Приложение 6.
Критические точки
распределения
![]() Фишера-Снедекора
Фишера-Снедекора
![]() –число
степеней свободы большей дисперсии,
–число
степеней свободы большей дисперсии,
![]() – число степеней свободы меньшей
дисперсии. Уровень значимости
– число степеней свободы меньшей
дисперсии. Уровень значимости![]()
|
к1 к2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
4052 |
4999 |
5403 |
5625 |
5764 |
5889 |
5928 |
5981 |
6022 |
6056 |
6082 |
6106 |
|
2 |
98,49 |
99,01 |
90,17 |
99,25 |
99,33 |
99,30 |
99,34 |
99,36 |
99,36 |
99,40 |
99,41 |
99,42 |
|
3 |
34,12 |
30,81 |
29,46 |
28,71 |
28,24 |
27,91 |
27,67 |
27,49 |
27,34 |
27,23 |
27,13 |
27,05 |
|
4 |
21,20 |
18,00 |
16,69 |
15,98 |
15,52 |
15,21 |
14,98 |
14,80 |
14,66 |
14,54 |
14,45 |
14,37 |
|
5 |
16,26 |
13,27 |
12,06 |
11,39 |
10,97 |
10,67 |
10,45 |
10,27 |
10,15 |
10,05 |
9,96 |
9,89 |
|
6 |
13,74 |
10.92 |
9,78 |
9,15 |
8,75 |
8,47 |
8,26 |
8,10 |
7,98 |
7,87 |
7,79 |
7,72 |
|
7 |
12,25 |
9,55 |
8,45 |
7,85 |
7,46 |
7,19 |
7,00 |
6,84 |
6,71 |
6,62 |
6,54 |
6,47 |
|
8 |
11,26 |
8,65 |
7,59 |
7,01 |
6,63 |
6,37 |
6,19 |
6,03 |
5,91 |
5,82 |
5,74 |
5,67 |
|
9 |
10,56 |
8,02 |
6,99 |
6,42 |
6,06 |
5,80 |
5,62 |
5,47 |
5,35 |
5,26 |
5,18 |
5,11 |
|
10 |
10,04 |
7,56 |
6,55 |
5,99 |
5,64 |
5,39 |
5,21 |
5,06 |
4,95 |
4,85 |
4,78 |
4,71 |
|
11 |
9,86 |
7,20 |
6,22 |
5,67 |
5,32 |
5,07 |
4,88 |
4,74 |
4,63 |
4,54 |
4,46 |
4,40 |
|
12 |
9,33 |
6,93 |
5,95 |
5,41 |
5,06 |
4,82 |
4,65 |
4,50 |
4,39 |
4,30 |
4,22 |
4,16 |
|
13 |
9,07 |
6,70 |
5,74 |
5,20 |
4,86 |
4,62 |
4,44 |
4,30 |
4,19 |
4,10 |
4,02 |
3,96 |
|
14 |
8,86 |
6,51 |
5,56 |
5,03 |
4,69 |
4,46 |
4,28 |
4,14 |
4,03 |
3,94 |
3,86 |
3,80 |
|
15 |
8,68 |
6,36 |
5,42 |
4,89 |
4,56 |
4,32 |
4,14 |
4,00 |
3,89 |
3,80 |
3,73 |
3,67 |
|
16 |
8,53 |
6,23 |
5,29 |
4,77 |
4,44 |
4,20 |
4,03 |
3,89 |
3,78 |
3,69 |
3,61 |
3,55 |
|
17 |
8,40 |
6,11 |
5,18 |
4,67 |
4,34 |
4,10 |
3,93 |
3,79 |
3,68 |
3,59 |
3,52 |
3,45 |




