учебное пособие - теория графов

1		0	1	0	1
	0	1	0	0	0
S	1	0	1	0	1	– матрица сильных компонент графа G.
0		0	0	1	0
	1	0	1	0	1

г) Найдем все сильные компоненты графа G. Ввиду определений 9.5 и 9.6, сильной компонентой графа G является максимальный сильно связный подграф графа G, т.е. такой подграф графа G, любые две вершины которого являются взаимно достижимыми и который не содержится ни в каком другом подграфе графа G с указанным свойством. Согласно теореме 8.2, вершины ai и aj графа G находятся в одной сильной компоненте (т.е. взаимно достижимы) тогда и только тогда, когда элемент sij матрицы сильных компонент S равен 1.

Так как s11= s13= s15=1, то вершины a1, a3 и a5 графа G находятся в одной сильной компоненте G1. Поскольку во второй строке матрицы S единственный элемент s22 равен 1, то вершина a2 графа G образует сильную компоненту G2. Аналогично, вершина a4 образует сильную компоненту G3. Таким образом, граф G имеет три сильные компоненты:

G1 (V1, R1 ) , где V1 a1, a3 , a5 , R1 u1,u4 ,u6 ,u7 ;

G2 (V2 , R2 ) , где V2 a2 , R2 ; G3 (V3 , R3 ) , где V3 a4 , R3 .

Тема 7. Метрические характеристики связных графов

Задание 7.1. Для связного неорграфа G найти: а) матрицу расстояний; б) эксцентриситеты всех вершин; в) диаметр и радиус;

141

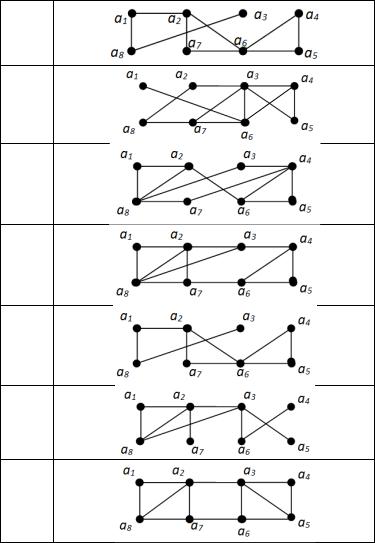
г) периферийные и центральные вершины.

7.1.1.

7.1.2.

7.1.3.

7.1.4.

7.1.5.

7.1.6.

7.1.7.

142

7.1.8.

7.1.9.

7.1.10.

Решение задания 7.1.1.

а) Найдем матрицу расстояний графа G. Поскольку граф G имеет 8 вершин, то, согласно определению 15.2, матрица расстояний P pij

графа G является матрицей 8-го порядка, причем элемент pij равен расстоянию d (ai , a j ) . По определению 15.1, d (ai , a j ) – длина кратчайшего

(ai , a j ) -маршрута в графе G. Тогда
d(a1, a1 ) 0 ,	d(a1, a2 ) 2 ,	d(a1, a3 ) 2 ,	d(a1, a4 ) 2 ,	d(a1, a5 ) 3,
d(a1, a6 ) 2 ,	d(a1, a7 ) 1,	d(a1, a8 ) 2 ,	d(a2 , a3 ) 1,	d(a2 , a4 ) 2 ,
d(a2 , a5 ) 2 ,	d(a2 , a6 ) 2 ,	d(a2 , a7 ) 1,	d(a2 , a8 ) 2 ,	d(a3 , a4 ) 1,
d(a3 , a5 ) 1,	d(a3 , a6 ) 1,	d(a3 , a7 ) 1,	d(a3 , a8 ) 1 ,	d(a4 , a5 ) 2 ,
d(a4 , a6 ) 2 ,	d(a4 , a7 ) 1,	d(a4 , a8 ) 2 ,	d(a5 , a6 ) 1,	d(a5 , a7 ) 1,
d(a5 , a8 ) 2 ,	d(a6 , a7 ) 1, d(a6 , a8 ) 2 , d(a7 , a8 ) 1, d(a2 , a2 ) 0 , …,
d(a8 , a8 ) 0 .

Отсюда следует, что матрица расстояний Р графа G имеет вид:

143

	0		2	2	2	3	2	1	2
		2	0	1	2	2	2	1	2
		2	1	0	1	1	1	1	1
P	2 2 1				0	2	2	1	2 .
		3	2	1	2	0	1	1	2
		2	2	1	2	1	0	1	2
		1	1	1	1	1	1	0	1
		2	2	1	2	2	2	1	0

б) Найдем эксцентриситеты всех вершин графа G. Согласно определению 15.3, эксцентриситет вершины a графа G есть число

e (a) max{ d(a,b) b V }. Ввиду замечания 15.3, эксцентриситет вершины ai равен наибольшему из чисел в i-й строке матрицы расстояний Р. Таким образом, получаем

e (a1 ) 3,	e (a2 ) 2,			e (a3 ) 2,			e (a4 ) 2,
e (a5 ) 3,	e (a6 ) 2,			e (a7 ) 1,			e (a8 ) 2.
в) Найдем диаметр и радиус графа G. Согласно определению 15.4,
диаметр	d (G) графа G есть наибольший из эксцентриситетов всех его
вершин, т.е. d(G) max{ e(a)						a V };		радиус	r(G) графа G есть наи-
меньший	из		эксцентриситетов					всех	его	вершин,	т.е.
r(G) min{ e(a)			a V } .

Исходя из пункта б), имеем d(G) 3, r(G) 1.

г) Найдем все периферийные и все центральные вершины графа G. По определению 15.5 вершина a графа G является периферийной, если e(a) d (G) ; вершина a графа G является центральной, если e(a) r(G) .

Так как e (a1 ) e (a5 ) 3 d(G) , то a1 и a5 – периферийные верши-

ны графа G. Так как e (a7 ) 1 r(G) , то a7 – центральная вершина графа

G.

144

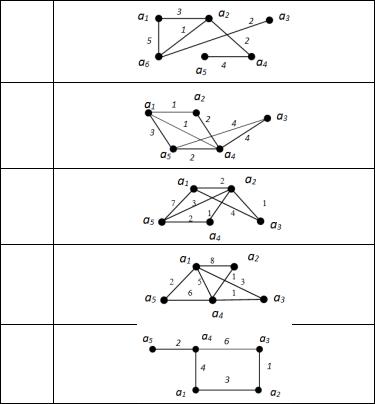
Задание 7.2. Для взвешенного связного неорграфа G найти: а) матрицу весов; б) взвешенные расстояния между вершинами;

в) взвешенные эксцентриситеты всех вершин; г) взвешенный диаметр и взвешенный радиус;

д) взвешенные периферийные и взвешенные центральные вершины.

7.2.1.

7.2.2.

7.2.3.

7.2.4.

7.2.5.

145

7.2.6.

7.2.7.

7.2.8.

7.2.9.

7.2.10.

Решение задания 7.2.1.

а) Найдем матрицу весов графа G. Поскольку граф G имеет 6 вершин, то, согласно определению 16.2, матрица весов W (wij ) графа G

является матрицей 6-го порядка, причем если в графе G имеется ребро (ai , a j ) , то элемент wij равен весу ребра (ai , a j ) , а если в графе G ребро (ai , a j ) отсутствует, то wij . Так как граф G содержит ребра [a1, a2 ],

146

[a1, a6 ] , [a2 , a4 ] , [a2 , a6 ] , [a3 , a6 ], [a4 , a5 ] , веса которых соответственно равны 3, 5, 2, 1, 2, 4, то матрица весов графа G имеет вид:

			3				5
		3			2		1
							2
	W							.
			2			4
					4
		5	1	2

б) Найдем взвешенные расстояния между вершинами графа G. По определению 16.4 взвешенное расстояние между вершинами a и b графа G – это наименьший из весов всех (a,b) -маршрутов графа G, который

обозначается dW (a,b) . Ввиду определения 16.3, вес маршрута есть сумма весов всех входящих в него ребер. Таким образом, получаем

dw (a1, a2 ) 3 , dw (a1, a3 ) 6 , dw (a1, a4 ) 5 , dw (a1, a5 ) 9 , dw (a1, a6 ) 4 , dw (a2 , a3 ) 3 , dw (a2 , a4 ) 2 , dw (a2 , a5 ) 6 , dw (a2 , a6 ) 1,

dw (a3 , a4 ) 5 , dw (a3 , a5 ) 9 , dw (a3 , a6 ) 2 , dw (a4 , a5 ) 4 , dw (a4 , a6 ) 3,

dw (a5 , a6 ) 7 .

в) Найдем взвешенные эксцентриситеты всех вершин графа G. Согласно определению 16.5, взвешенный эксцентриситет вершины a графа

G есть число eW (a) max{ dW (a,b)					b V } . Тогда из пункта б) следует
e w(a1 ) 9, e w (a2 ) 6, e w (a3 ) 9, e w (a4 ) 5, e w (a5 ) 9, e w (a6 ) 7.
г) Найдем взвешенный диаметр dw (G)						и взвешенный радиус rw (G)
графа G. По			определению		16.6	dW (G) max{ eW (a)		a V },
rW (G) min{ eW (a)			a V }.			rw (G) 5 .
Исходя из пункта б), имеем dw (G) 9 ,
					147

д) Найдем все взвешенные периферийные и все взвешенные центральные вершины графа G. Ввиду определения 16.7, вершина a графа G является взвешенной периферийной вершиной, если ew (a) dw (G) ;

вершина a графа G является взвешенной центральной, если ew (a) rw (G) .

Так как e w(a1 ) ew (a3 ) ew (a5 ) 9 dw (G) , то a1, a3, a5 – взвешенные периферийные вершины графа G. Так как e w(a4 ) 5 rw (G) , то a4 – взвешенная центральная вершина графа G.

Тема 8. Нахождение в графах путей минимального и максимального весов

Задание 8.1. Для взвешенного орграфа G, заданного матрицей весов W, с помощью метода Шимбелла найти:

а) путь минимального веса длины 3; б) путь максимального веса длины 3.

8.1.1.			5	13	9	12			8.1.6.				3	2		5
			9											12
					5 6
							15				4				5 10
	W									W
			6		8		9
													7
												6
						1

148

8.1.2.			1		2	3				8.1.7.			2	3
			4											7
							2									4
	W	5 7			5						W	5		6 1
							1									3
		8 3					9					1		3		6
8.1.3.				8	9	10				8.1.8.				1		3
														5 8
					3 7 13
			5											9
	W						11				W					4
			2		4		6					2		4 7
		4										4
												6
8.1.4.			5		8	9				8.1.9.			5	2
			7											7 11
					1							2		9 6
	W										W
			3		4
																5
		4 9					1									6
8.1.5.			2	1		3				8.1.10.			2	5		8
			4		2								4
					3 6 2							7
	W				1						W	4		2 7
							5									1
			2				1									10

Решение задания 8.1.1.

Метод Шимбелла нахождения во взвешенных орграфах пути минимального (максимального) веса, содержащего заданное количество k ребер состоит из следующих этапов:

1 этап. В матрице весов W графа G заменить все символы – и символом 0.

149

2 этап. Найти W k	W W W	(найти W k	W W W ), ис-
min		max
	k раз		k раз

пользуя при умножении матриц следующее правило (*): для любых элементов a и b матриц:

a b 0			a 0 или	b 0 ;
если a 0	и b 0 ,
то a b a b ,
a b min{a,b}		( a b max{a,b} – при нахождении W k				).
					max
3 этап. Пусть w	– наименьший элемент в матрице W k				(наибольший
ij				min

элемент в матрице Wmaxk ). Тогда wij – минимальный (максималь-

ный) вес пути графа G, состоящий из k ребер, причем данный путь соединяет i-ю и j-ю вершины графа G.

а) С помощью метода Шимбелла найдем в графе G один из путей минимального веса.

1 этап. В матрице весов W графа G заменим все символы – и символом 0:

		0		5	13	9	12	0
			0	0	9	5	6	0
			0	0	0	0	0	15	.
	W
		0		0	6	0	8	9
			0	0	0	0	0	0
			0	0	0	0	1	0
2 этап. Найдем W 3	W W W , используя правило (*):
min

150