учебное пособие - теория графов

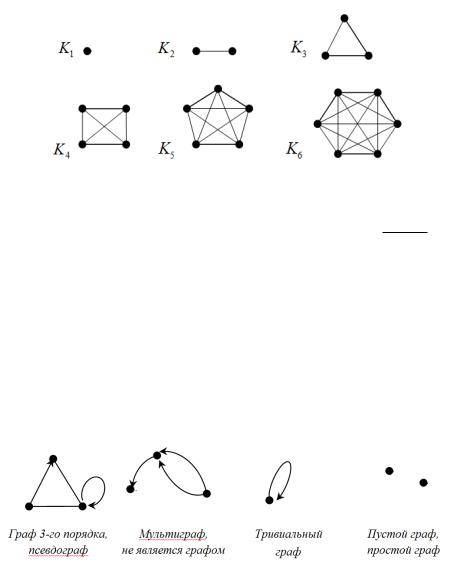
Например:

Лемма 1.1. Пусть m – число ребер графа Kn . Тогда т п(п 1) .

2

Доказательство. В полном графе любые две различные вершины являются смежными. Это означает, что каждая из n вершин в графе Kn

имеет (n–1) инцидентных ей ребер. Ввиду того, что каждое ребро является инцидентным по отношению к двум вершинам, то число ребер в графе

Kn	равно ((n 1) (n 1) ... (n 1))	1		n(n 1)	. Лемма доказана.
		2	2
	n раз

Пример 1.2.

11

Граф как алгебраическая система

Пусть G V , R, f – орграф. Тогда каждое ребро u графа G однозначно определяется упорядоченной парой вершин a,b , соединенных им. В этой связи ребро u можно обозначать упорядоченной парой a,b ,

где a – начало ребра u, b – конец ребра u, т.е. f (u) u . Таким образом, в

(a,b)

орграфе G множество R играет роль бинарного отношения на множестве

V, т.е.

R u a,b V V | реброu исходит из вершины a и заходит в вершину b .

Напомним, что непустое множество с определенными на нем алгебраическими операциями и отношениями называется алгебраической системой. Используя определение алгебраической системы, сформулируем следующее определение графа.

Определение 1.6 . Пусть V – непустое множество, R – бинарное отношение на V. Графом называется алгебраическая система V , R .

Замечание 1.3. Если R – симметричное бинарное отношение, то заменяя упорядоченные пары вида a, b и b, a элементом a, b , получим граф, у которого все ребра неориентированные. Таким образом, каждый неориентированный граф можно рассматривать как орграф с симметричным бинарным отношением.

Части и подграфы графа

Определение 1.17. Пусть G (V , R) – граф. Граф G1 (V1 , R1 ) называется частью графа G, если V1 V и R1 R V12 .

Определение 1.18. Часть G1 (V1 , R1 ) графа G (V , R) называется

подграфом (правильным подграфом) графа G, если R1 R V12 .

Пример 1.3.

12

Пусть G (V , R) , V {1,2,3,4}, R {(1,3),[1,2],[2,3],[3,4],[4,1] },

G1 (V1 ,R1 ), V1 {1,2,3 },	R1 {[1,2],(3,2)}, G2	(V2 ,R2 ),	V2 V1 ,
R2 {[1,2],[2,3],(1,3)}. Определить являются ли G1		и G2 частями, под-
графами графа G.

	Решение: Найдем R V 2		: R V 2 {(1,3),[1,2],[2,3]}. Тогда
		1	1
R R V 2		G – часть графа G, подграфом не является;
1	1	1
R R V 2		G – подграф графа G.
2	1	2

§ 2. Вершины графа и их числовые характеристики

Содержание параграфа

степень (валентность) вершины графа;

изолированные и концевые (висячие) вершины, концевое ребро;

степень графа;

полустепень исхода из вершины (захода в вершину);

теорема Эйлера о рукопожатиях.

Определение 2.1. Степенью (валентностью) вершины a графа G

называется число рёбер, ей инцидентных, причём петли считаются дважды, и обозначается deg a (или, иначе, n(a), d(a)).

Пример 2.1.

deg a 1 ,

degb 4 , deg c 1,

deg d 0

Определение 2.2. Вершина a графа G называется

13

1)изолированной, если deg a 0 ;

2)висящей или концевой, если deg a 1 .

Определение 2.3. Ребро графа называется концевым ребром, если оно инцидентно концевой вершине.

Определение 2.4. Степенью графа G называется наибольшая из степеней всех его вершин и обозначается deg G .

Замечание 2.1. Через δ(G) обозначается наименьшая из степеней всех вершин графа G, через (G) – наибольшая из степеней всех вершин графа G. Следовательно, deg G = (G) .

Пусть G – ориентированный граф, a – вершина графа G. Введем следующие обозначения: deg a – число рёбер графа G, исходящих из вершины a; deg a – число рёбер графа G, заходящих в вершину a. Тогда deg a deg a deg a .

Определение 2.5. Пусть a – вершина орграфа G. Число deg a называется полустепенью исхода из вершины a, число deg a называется

полустепенью захода в вершину a.
	Определение 2.6.
1.	Вершина a орграфа G называется источником, если			deg a 0	и
	deg a 0 .
2.	Вершина a орграфа G называется стоком,		если	deg a 0	и
	deg a 0.
	Замечание 2.2. Пусть G V , R,	f – орграф	f – инъективное
отображение, f : R V 2 . Напомним,		что если f u a,b , то u – про-

образ элемента a,b при отображении f, а a,b – образ элемента u при отображении f.

Кроме того, f R f u | u R – образ множества R при отображении f; f 1 a,b u R | f u a,b – полный прообраз элемента

14

a,b при	отображении f. Так как f – инъективное отображение, то
f 1 a,b –	одноэлементное множество. Напомним, что если Y V V ,
то f 1 Y	f 1 a,b – полный прообраз множества Y при отображе-
	а ,в Y
нии f. В частности, f 1 V V R . Отметим, что			f 1 a V		deg		a ,

f 1 V a deg a .

Теорема 2.1. Пусть

G V , R, f

–

конечный

ориентированный

граф. Тогда справедливы следующие утверждения:

1.

deg a deg a

R

.

a V

a V

2.

Сумма степеней всех вершин графа G равна удвоенному числу рёбер

графа G, т.е. deg a 2

R

.

a V

Доказательство. 1) Покажем,

что deg a

R

. Из замечания 2.2

следует, что f 1 V V R .

Рассмотрим V V a,b | a,b V . Введём

обозначение

V 2

a V a,b

b V , a V

a

V V

V 2

f 1 V V

V 2

f 1 V 2

R

f 1

a

a

a

a V

a V

a V

f 1 Va2

f 1 a V

замечание 2.2

deg a.

a V

a V

a V

Аналогично доказывается, что deg a R .

a V

2) deg a deg a deg a R R 2 R . Теорема доказана.

a V

a V

Из теоремы 2.1 в качестве следствия получаем теорему Эйлера о рукопожатиях.

15

Следствие 2.1.1 (теорема Эйлера о рукопожатиях). В любом ко-

нечном ориентированном графе число вершин нечётной степени является четным числом.

Доказательство. Пусть G V , R, f , V1 – множество всех вершин графа G чётной степени, V2 – множество всех вершин графа G нечётной степени, то есть

V1 a V | dega 2ka ,ka Z } , V2 { b V | deg b 2kb 1,kb Z}.

Из теоремы 2.1 следует, что

2

R

deg a deg a deg b 2kа

(2kb 1)

a V

a V1

b V2

a V1

b V2

2

kа

kb

V2

a V1

b V2

V2

2

R

2

kа

V2

kb

–

чётное число. Следствие до-

a V1

b V2

казано.

Замечание 2.3. Теорему Эйлера можно интерпретировать так: на любом мероприятии количество человек, сделавших нечетное число рукопожатий, является чётным числом или таких людей нет.

§ 3. Регулярные и двудольные графы

Содержание параграфа

регулярный (однородный) граф;

регулярность полного графа;

двудольные и полные двудольные граф;

свойства регулярных двудольных графов;

звездный граф;

k-дольные графы.

16

Определение 3.1. Граф G называется регулярным (однородным),

если все его вершины имеют одну и ту же степень.

Пустой граф является регулярным графом степени 0. Регулярные графы степени 3 называют также кубическими или трехвалентными. Примером кубического графа является граф Петерсона:

Лемма 3.1. Полный граф n-го порядка является регулярным графом степени n–1.

Доказательство. Поскольку в полном графе любые две различные вершины являются смежными, то для всякой вершины a графа Kn справедливо равенство deg a n 1. Это означает, Kn – регулярный граф и

deg Kn n 1. Лемма доказана.

Лемма 3.2. Не существует регулярного графа n-го порядка степени k, у которого k и n нечетные.

	Доказательство.		Допустим, что существует регулярный					граф
			n ,			deg G k , где k и n – нечетные числа.
G=(V,R) такой, что		V						Тогда
	deg a k k ... k n k						– нечетное число. С другой стороны, по
a V	n раз
теореме 2.1 deg a 2					R		– четное число. Получили противоречие.
	a V

Следовательно, регулярного графа n-го порядка степени k, где k и n – нечетные числа, не существует. Лемма доказана.

17

Теорема 3.1. Пусть n и k – натуральные числа различной четности, 0 k n 1. Тогда существует регулярный граф n-го порядка степени k.

Определение 3.2. Граф G=(V,R) называется двудольным, если существует разбиение V1, V2 множества V (множества V1 и V2 называются долями графа G) такое, что каждое ребро графа G имеет концы, принадлежащие различным долям.

Определение 3.3. Двудольный граф G называется полным двудольным графом, если любые две вершины графа G, принадлежащие разным долям, являются смежными.

Полный двудольный граф, у которого m вершин принадлежит одной доле, n вершин принадлежит другой доле, обозначается Km,n.

Например, K3,3 :

Определение 3.4. Двудольный граф K1,n называется звездным гра-

фом.

Например, K1,6 :

Теорема 3.2. Пусть G=(V,R) – непустой регулярный двудольный граф, V1 и V2 – доли графа G. Тогда V1 V2 .

18

Доказательство. Так как G – непустой регулярный граф, тоa V : deg a k , где k – некоторое натуральное число. Поскольку граф

G является двудольным, то

R

V1

k и

R

V2

k . Отсюда следует,

что

V1

V2

. Теорема доказана.

Определение 3.5. Граф G=(V,R) называется k-дольным, если существует разбиение V1,V2,…,Vk множества V (множества V1,V2,…,Vk называются долями графа G) такое, что каждое ребро графа G имеет концы, принадлежащие различным долям.

§4. Способы задания графов

Содержание параграфа

основные способы задания графов (аналитический, геометрический, матричный, с помощью списка дуг, структурой смежности);

матрицы смежности и инцидентности, матрица Кирхгофа;

представление графов в памяти ЭВМ.

Основными способами задания графов являются следующие.

1.Графический (геометрический) способ – заключается в изображении графа на плоскости или в трехмерном пространстве.

2.Аналитический способ – заключается в непосредственном перечисление элементов множеств V и R для графа G (V , R) .

3.Матричный способ.

Определение 4.1. Пусть G (V , R) – ориентированный граф, V {a1 , a2 ,..., an }. Матрицей смежности графа G называется матрица

19

a

a

...

a

11

12

1n

AG

n-го

порядка

вида

AG

... ...

...

...

,

где

an2

...

an1

ann

i

j

) R

1, если ( a ,a

aij

,

i 1, n,

j 1, n .

,a j ) R

0, если ( ai

Замечание 4.1. Для произвольного графа G можно рассматривать соответствующий ему ориентированный граф, обозначаемый Gор, который получают из графа G заменой каждого неориентированного ребра парой ориентированных ребер с противоположной ориентацией. В силу сказанного, справедливо следующее определение.

Определение 4.2. Матрицей смежности произвольного графа G называется матрица смежности соответствующего ему ориентированного графа Gор.

Пример 4.1. Составим матрицу смежности следующего графа G:

Решение:

	1		1	0	0	0
		0	0	1	0	0
A		0	0	0	0	0
G
	0		0	1	1	0
		0	0	0	0	0
								.

Пример 4.2. Граф G задан матрицей смежности AG . Изобразим G графически.

20