П.5 Уравнения и тождества

В уравнении как бы ставится вопрос о том, когда функция становится равной некоторому конкретному числу. Примерами уравнений являются

2x = 8

x² = 9

f(x) = 0.

Решением уравнения является значение x, удовлетворяющее данному уравнению. Первое уравнение имеет решение x = 4. Второе уравнение имеет два решения x = 3 и x = —3. Третье уравнение задано просто в общем виде. Мы не знаем его решения до тех пор, пока нам неизвестно конкретное правило, стоящее за f, но мы можем обозначить его решение через x*9. Это просто означает, что x*10 есть такое число, что f(x*) = 011. Мы говорим, что x*12 удовлетворяет уравнению f(x) = 0.

Тождество есть взаимосвязь между переменными, которая справедлива для всех значений переменных. Вот некоторые примеры тождеств:

(x + y)² x² + 2xy + y²

2(x + 1) 2x +2.

Особый знак 13 означает, что левая и правая части выражения равны для всех значений переменных. Уравнение справедливо только для некоторых значений переменных, в то время как тождество справедливо для всех значений переменных. Часто тождество справедливо по самому определению тех понятий, о которых идет речь.

П.6 Линейные функции

Линейная функция есть функция вида

y = ax + b,

где a и b — константы. Примерами линейных функций являются

y = 2x + 3

y = x — 99.

Строго говоря, функция вида y = ax + b должна называться афинной функцией и только функции вида y = ax должны называться линейными функциями. Однако мы не будем настаивать на этом разграничении.

Линейные функции могут быть также выражены неявно, в виде, подобном ax + by = c.

В таком случае мы часто выражаем y как функцию x, чтобы привести это к "стандартному" виду:

y = — x.

П.7 Изменения и отношения изменений

Обозначение Dx 14 читается как "изменение x". Оно не означает D15, умноженная на x. Если x изменяется от x*16 до x**17, то изменение x есть просто

Dx = x** — x*.18

Мы также можем записать

x** = x* + x19,

указывая на то, что x**20 есть x*21 плюс изменение x.

Как правило, Dx 22 относится к малому изменению x. Иногда мы выражаем эту мысль, говоря, что Dx 23 представляет предельное изменение.

Скорость изменения есть отношение двух изменений. Если y есть функция x, заданная в виде y = f(x), то скорость изменения y относительно x обозначается как

=.

Скорость изменения показывает то, как изменяется y с изменением x.

Линейная функция обладает тем свойством, что скорость изменения y относительно x является постоянной. Чтобы доказать это, обратите внимание, что если y = a + bx, то

=== b.

Для нелинейных функций скорость изменения функции будет зависеть от значения x. Рассмотрим, например, функцию y = x²24. Для этой функции

=== 2x + Dx.

Здесь скорость изменения от x до x + Dx25 зависит от значения x и от величины изменения Dx26. Но если рассматривать очень малые изменения x, то Dx2728 будет почти равна нулю, так что скорость изменения y относительно x составит примерно 2x.

П.8 Наклоны и пересечения с осями

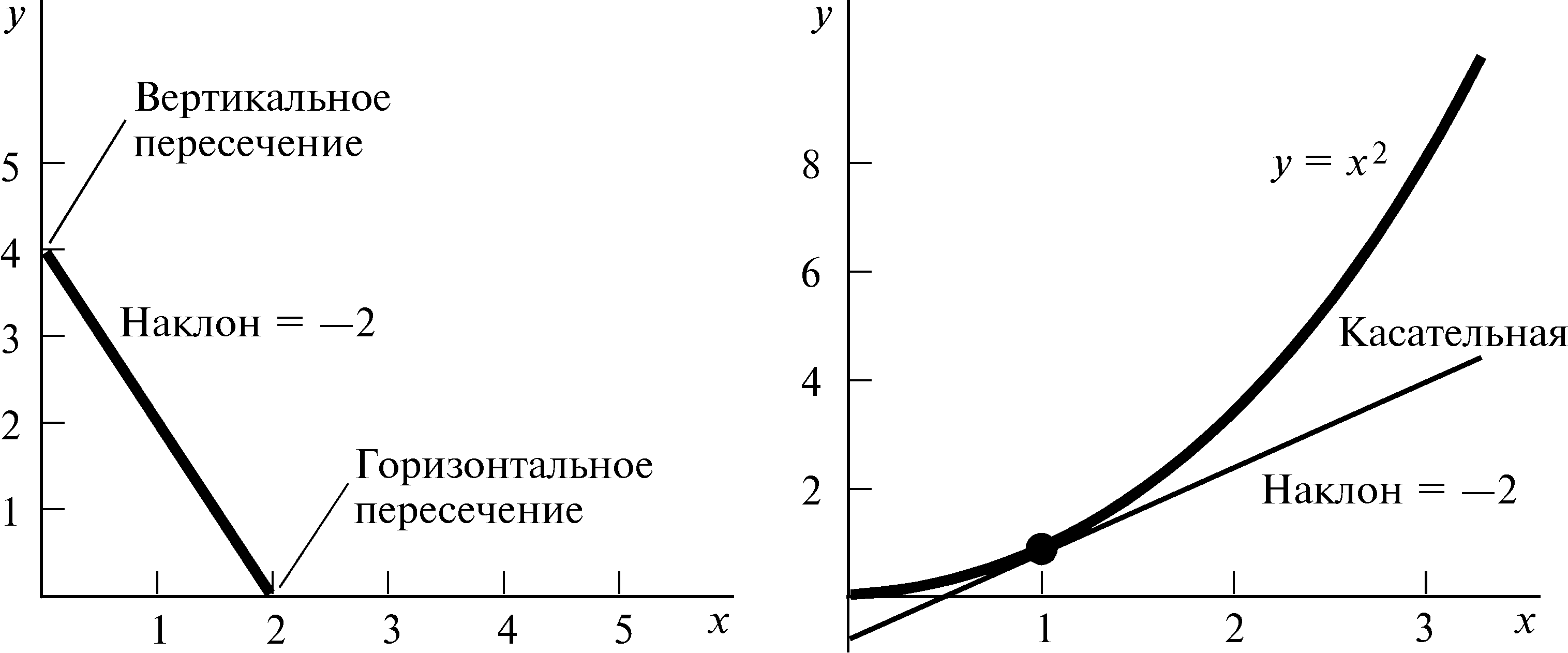
Скорость изменения функции может быть графически интерпретирована как наклон функции. На рис.П.2A мы изобразили линейную функцию y = —2x + 4. Точка пересечения графика этой функции с вертикальной осью (вертикальное пересечение) есть значение y при x = 0, составляющее y = 4. Точка пересечения с горизонтальной осью (горизонтальное пересечение) есть значение x при y = 0, составляющее x = 2. Наклон функции есть скорость изменения y при изменении x. В этом случае наклон функции равен —2.

A B

Наклоны и точки пересечения с осями. На рис.A изображена функция y = —2x + 4, а на рис.B — функция y = x^229.

Рис. П.2

Вообще, если линейная функция имеет вид y = ax + b, то точка пересечения с вертикальной осью будет y* = b30, а точка пересечения с горизонтальной осью x* = —b/a31. Если линейная функция представлена в виде

a₁x₁ + a₂x₂ = c,

то горизонтальным пересечением будет значение x₁32 при x₂ = 033, равное = c/a₁34, а вертикальное пересечение будет иметь место при x₁ = 035, т.е. при = c/a₂36. Наклон этой функции есть —a₁/a₂37.

Нелинейная функция обладает тем свойством, что ее наклон изменяется по мере изменения x. Касательная к функции в некоторой точке x есть линейная функция, имеющая тот же самый наклон. На рис.П.2B мы изобразили функцию y = x²38 и касательную к ней в точке x = 1.

Если y всегда растет с ростом x, то Dy 39 всегда будет иметь тот же знак, что и Dx 40, так что наклон функции будет положительным. Если, с другой стороны, y убывает с ростом x или y возрастает с убыванием x, то Dy41 и Dx42 будут иметь противоположные знаки, так что наклон функции будет отрицательным.