Лекция 2 +

9

2. Элементарная теория вероятностей

ЛЕКЦИЯ 2

Аксиомы теории вероятностей. Основанием современной теории вероятностей служит система аксиом, установленная А. Н. Колмогоровым.

Пусть – пространство элементарных событий и – алгебра определённых на пространстве событий. Тогда вероятность определяется следующими аксиомами.

2. Каждому событию соответствует действительное число , называемое вероятностью события , причём .

2. Вероятность достоверного события .

3. Если события и не пересекаются, то вероятность их объединения равна сумме их вероятностей:

.

Приведённые аксиомы теории вероятностей представляют собой абстрактные эквиваленты приведённых выше свойств относительной частоты (2.4) – (2.5). Аксиома 1 постулирует статистическую устойчивость относительной частоты появления некоторого события в длинных сериях испытаний, то есть статистическое определение вероятности 2.5, и отражает свойство относительной частоты события (2.4). Аксиома 2 постулирует появление какого-либо (любого) результат (исхода) из всех возможных исходов данного эксперимента. Аксиома 3 обобщает свойство (2.5) относительной частоты, относящееся к частоте появления объединения двух несовместимых событий.

Теорема сложения вероятностей для несовместимых событий. Пусть – совокупность несовместимых событий. Справедлива следующая теорема.

Теорема 2.1. Для несовместимых событий вероятность появления события вычисляется по формуле

. (2.6)

Д о к а з а т е л ь с т в о. Доказательство непосредственно следует из аксиомы 3 и определения несовместимых событий 2.15. Действительно, так как , то с учётом ассоциативности операции объединения и в соответствии с аксиомой 3 имеем:

.

Теорема 2.2. Если несовместимые события образуют полную группу, то вероятность их объединения равна единице:

. (2.7)

Д о к а з а т е л ь с т в о. Так как несовместимые события образуют полную группу, то одно из них происходит обязательно. Поэтому событие , то есть является достоверным. Применяя аксиому 2, получаем доказательство теоремы.

Полная группа событий может включать в себя счётное число событий, причём при . Тогда формула (2.7) принимает вид

. (2.8)

Теорема 2.3. Вероятность объединения двух противоположных событий и равна единице:

. (2.9)

Д о к а з а т е л ь с т в о. Так как события и несовместимы и одно из них происходит обязательно, то они образуют полную группу и, следовательно, формула (2.9) получается из формулы (2.7) как частный случай последней.

Формула (2.4) часто используется в виде

. (2.10)

Определение 2.1. События называются равновероятными, если вероятности их появления в данном испытании равны:

.

Лемма 2.1. Вероятность появления одного из несовместимых равновероятных событий, составляющих полную группу, вычисляется по формуле

. (2.11)

Д о к а з а т е л ь с т в о. Применяя формулу (2.7) и учитывая определение 2.19, получаем:

.

Теорема 2.4. Вероятность появления одного из событий, входящих в полную группу равновероятных событий , вычисляется по формуле

. (2.12)

Д о к а з а т е л ь с т в о. Используя формулы (2.8) и (2.11), получаем:

.

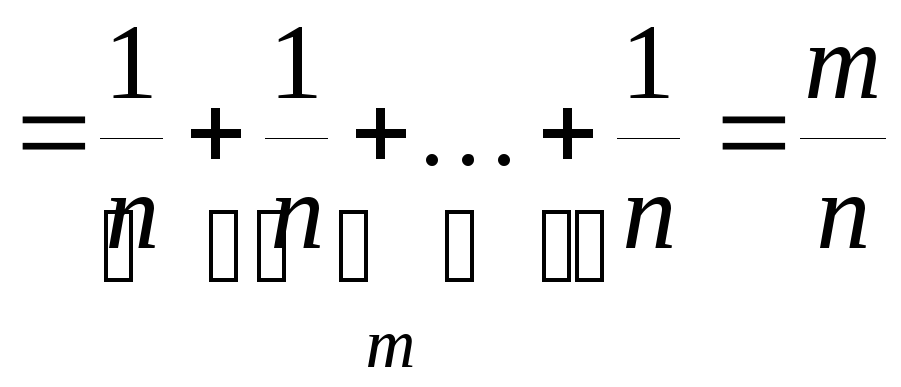Если равновероятных элементарных событий из пространства элементарных событий благоприятствуют некоторому событию , то формула (2.12) в классической теории вероятностей принимается за определение вероятности.

Пример 2.1. Найти вероятность выпадения какой-либо цифры при однократном бросании игральной кости.

Р е ш е н и е. Так как события

,

,

,

равновероятны и образуют полную группу, то, применяя формулу (2.11), получаем, что вероятность выпадения какой-либо цифры

, .

Пример 2.2. В лотерее разыгрывается 1000 билетов. Из них: на 1 билет выпадает выигрыш 500 рублей; на 10 билетов выпадает выигрыш по 100 рублей; на 50 билетов выпадает выигрыш по 20 рублей; на 100 билетов выпадает выигрыш по 5 рублей; остальные билеты невыигрышные. Некто покупает 1 билет. Требуется найти вероятность выигрыша не менее 20 рублей.

Р е ш е н и е. Рассмотрим следующие события:

;

;

;

.

Событие представим в виде

.

В силу несовместимости событий по теореме сложения вероятностей для несовместимых событий получаем:

.

Из того, что все исходы в задаче равновероятны и образуют полную группу, из теоремы 2.4 следует, что

,

,

.

Поэтому для искомой вероятности события получаем

.

Условные вероятности, правило умножения вероятностей. Не все события являются независимыми. Возможность появления какого-либо события часто зависит от того, произошло, или нет другое событие.

Определение 2.2. Два события и называются зависимыми (независимыми), если вероятность появления одного из них зависит (не зависит) от того, произошло или нет другое событие.

Определение 2.3. Пусть события и зависимы и . Тогда условной вероятностью события называется величина, вычисляемая по формуле

. (2.13)

Таким образом, условная вероятность события – вероятность этого события, вычисленная в предположении, что событие уже произошло.

Формулу (2.13) чаще записывают в виде правила умножения вероятностей:

. (2.14)

Так как можно выбрать «первым» событие , то вместо (2.14) можно записать

. (2.15)

Безусловные вероятности , и условные вероятности , в формулах (2.13) – (2.15) называются, соответственно, априорными и апостериорными вероятностями.

Очевидным образом для независимых событий апостериорные вероятности превращаются в априорные вероятности

,

и из (2.13), получаем

. (2.16)

Равенство (2.16) может служить определением независимости событий, и естественным образом распространяется на произвольное число событий, независимых в совокупности.

Определение 2.4. События называются независимыми в совокупности, если вероятность их совместного появления в данном эксперименте равна произведению вероятностей появления каждого из них.

Таким образом, для независимых событий имеем

. (2.17)

Пример 2.3. В ящике имеется 2 белых и 3 чёрных шара. Производится два испытания, каждое из которых состоит в изъятии из ящика одного шара, причём после первого испытания шар возвращается обратно в ящик. Пусть в результате первого испытания произошло событие

{изъят белый шар},

а в результате второго испытания произошло событие

{изъят чёрный шар}.

Так как после первого испытания шар возвращается в ящик, то события и независимы и .

Пример 2.4. Пусть в условиях предыдущего примера производится испытание – изъятие из ящика одного шара, который назад в ящик не возвращается. Предположим, что в результате первого испытания происходит событие

{изъят белый шар}.

Вероятность этого события есть .

Производится второе испытание, в результате которого происходит событие

{изъят чёрный шар}.

Так как после первого испытания шар в ящик не возвращён, вероятность второго события , то есть увеличилась. Событие зависит от события .

Пример 2.5. Пусть, как и в предыдущих примерах, в ящике имеется 2 белых и три чёрных шара. Предположим, что из ящика два раза изымается по одному шару, причём после первого изъятия шар назад в ящик не возвращается. Требуется определить вероятность того, что оба раза изъят белый шар.

Р е ш е н и е. Результатом первого испытания является событие

{изъят белый шар}.

Результатом второго испытания является событие

{изъят белый шар}.

Результирующее событие

{оба раза из ящика изымается белый шар}.

Используем теорему умножения вероятностей для зависимых событий:

.

Причём

.

Следовательно,

.

Теорема сложения вероятностей для совместимых событий. Рассмотрим, теперь, случай, когда события совместимы. Справедлива следующая теорема.

Теорема 2.5. Пусть события (зависимые или нет!) совместимы. Тогда вероятность их объединения (суммы) вычисляется по формуле

, (2.18)

где

,

,

,

,

.

Эта теорема принимается без доказательства.

Первое слагаемое в (2.18) всегда равно сумме вероятностей, то есть соответствует сложению вероятностей для несовместимых событий, а остальные слагаемые дают поправку на совместимость событий. Когда вероятностями совместного появления событий можно пренебречь по сравнению с вероятностями появления самих событий, можно использовать для приближённого вычисления вероятности объединения (суммы) совместимых событий формулу (2.6) для вероятности появления суммы несовместимых событий.

Формула (2.18), например, при имеет вид

. (2.19)

Формула полной вероятности. Предположим, что некоторое событие может произойти только совместно с одним из взаимно несовместимых событий , образующих полную группу. В этом предположении события называют гипотезами, в отношении случайного события .

Теорема 2.6. Если – гипотезы в отношении события , то вероятность появления события вычисляется по формуле:

. (2.20)

Д о к а з а т е л ь с т в о. Представим событие в виде

.

Гипотезы несовместимы, следовательно, несовместимы и все события . Применяя формулу сложения вероятностей несовместимых событий, получаем

.

Учитывая, что по формуле умножения вероятностей (2.14) каждая вероятность

,

получаем искомую формулу (2.20).

Формула (2.20) называется формулой полной вероятности. Эта формула позволяет вычислить вероятность появления события , если известны априорные вероятности гипотез и апостериорные вероятности события при условии, что соответствующая гипотеза реализовалась.

Пример 2.6. Для приёма зачёта экзаменатор приготовил 50 задач: 30 по дифференциальному исчислению и 20 по интегральному исчислению. Для того чтобы сдать зачёт, нужно решить первую попавшуюся задачу. Какова вероятность студенту сдать зачёт, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению.

Р е ш е н и е. Выпишем гипотезы:

{получена задача по дифференциальному исчислению},

{ получена задача по интегральному исчислению}.

Для вероятностей гипотез имеем:

Пусть событие

{задача решена}.

Тогда по формуле полной вероятности получаем

,

где , . Окончательно для вероятности события имеем:

.

Формула Байеса. Иногда требуется решить следующую задачу: найти апостериорную вероятность гипотезы при условии, что событие реализовалось, причём предполагается, что априорные вероятности гипотез и апостериорные вероятности события известны. Иными словами, нужно ответить на вопрос: как изменились вероятности гипотез в связи с появлением события ?

Пусть, как и в предыдущем параграфе, гипотезы образуют полную группу. Используя формулы умножения вероятностей (2.13) и (2.14), находим:

. (2.21)

Подставляя в (2.21) вероятность по формуле полной вероятности (2.20) , получаем так называемую формулу Байеса

, (2.22)

которая и решает поставленную задачу.

Пример 2.7. Партия деталей изготовлена тремя рабочими, причём каждый из них при изготовлении деталей допустил некоторый процент брака. Количество деталей (в процентах), изготовленных каждым рабочим, и соответствующий процент допущенного брака приведены в таблице

Рабочий	1-й	2-й	3-й
Количество	25 %	35 %	40 %
Процент брака	5 %	4 %	2 %

Случайно выбранная для проверки деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена вторым рабочим?

Р е ш е н и е. Пусть события

{выбранная деталь бракованная},

{бракованная деталь изготовлена первым рабочим},

{бракованная деталь изготовлена вторым рабочим},

{бракованная деталь изготовлена третьим рабочим}.

Вероятности распределяются так:

Используя формулу Байеса (2.22), получаем:

.

Последовательность независимых испытаний, биномиальная формула. Рассмотрим последовательность (серию) из испытаний. Предположим, что в каждом испытании может появиться некоторое событие с одной и той же отличной от нуля вероятностью , независящей от исхода других испытаний. Такая последовательность независимых испытаний называется схемой Бернулли.

Так как вероятность появления события в одном испытании равна , то вероятность противоположного события (не появления события в том же испытании) равна .