(5.10)

где

при

и

при

.

5.3 Механический смысл стоксовых постоянных

Рассмотрим сначала случай, когда . Тогда и , так как эта переменная изменяется от нуля до . Поскольку гармоника также равна нулю, остается определить только . Из формулы (5.10) следует

(5.11)

Рассмотрим теперь случай, когда . Теперь мы должны определить четыре стоксовых постоянных: , , , . Обращаясь к формуле (5.10), получим

(5.12)

(5.13)

Для того, чтобы выполнить интегрирование, нужно перейти к декартовым координатам

(5.14)

По определению сферических гармоник имеет место равенство

(5.15)

При	имеем		, поэтому

Из теоретической механики известно, что координаты центра масс тела определяются следующим образом

поэтому

(5.16)

Итак, шаровая функция первой степени, которую представляет собой функция Лапласа первой степени, определяет центр масс притягивающего тела. Определим теперь функцию Лапласа второй степени. Из формулы (5.7) следует

Снова перейдем к декартовым координатам

(5.17)

Следуя правилам теоретической механики, выполним интегрирование. Будем использовать традиционные обозначения для моментов массы второго порядка -- моментов инерции

(5.18)

Для того, чтобы привести формулу для коэффициентов к окончательному виду, заметим, что

Следовательно, матрицу, составленную из коэффициентов разложения потенциала притяжения для шаровой функции второй степени, можно представить в виде

(5.19)

Вернемся к формуле представления гравитационного потенциала рядом Лапласа. Определяя стоксовы постоянные через ненормированные шаровые функции, формула (5.9) будет иметь тот же вид, за исключением того, что стоксовы постоянные и сферические функции "потеряют" черту сверху

(5.20)

где коэффициенты и определяются формулами (5.10), (5.16) и (5.19). Полученную формулу можно упростить, если принять

1.начало координат совпадает с центром масс,

2.направление осей совпадают с главными осями инерции.

При выполнении этих условий функция Лапласа первой степени будет равна нулю,

то есть		. Кроме того, будут равны нулю и произведения инерции
, , . Следовательно,				, а

Теперь формула (5.20) принимает вид

(5.21)

Полученная формула говорит о том, что потенциал притяжения в точке 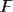зависит как от расстояния рассматриваемой точки от начала координат, так и сферических координат: полярного расстояния и долготы. Однако отдельные сферические гармоники могут зависеть только от широты, например, при , в этом случае гармоники называют зональными. Поверхность сферы в этом случае оказывается разбитой на зоны -- сферические пояса.

Второй крайний случай возникает при 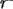. Обратимся к формуле (5.15). В этом случае она приобретает вид

Нетрудно понять, что знак сферическая гармоника может менять при определенных значениях долготы, так как -ая производная полинома -ой степени есть постоянная величина, а 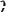при изменении полярного расстояния от нуля до не меняет знака. Поверхность сферы оказывается разбитой подобно арбузу на сектора и соответствующие гармоники, называются секториальными.

Наконец, в остальных случаях границы изменения знака сферической гармоники на поверхности сферы образуют мозаику подобно шахматной доске. Эти гармоники называют тессеральными от латинского слова tessera, что означает сферический четырехугольник в мозаике.