ИнМu_lectures

∆ Кратное интегрирование. Когомологии

71

Пусть ω = P|I|=p	′aIdxI	– форма степени p ≥ 1. По определения формы
(dω(x))y	=	′daI(x)dxI		=	daI(x(y))dxI(y).
	|XI|			y	X
		=p
С другой стороны
d(ω(x(y))) = d				′aI(x(y))dxI(y) .
			|XI|
			=p

Отсюда по линейности дифференциала и используя свойства внешнего произведения получаем, что

|X|	′	|XI|
d(ω(x(y))) =	daI(x(y)) dxI(y) +	aI(x(y)) d(dxI(y)).
I =p		=p

И, наконец, используя обобщенное правило Лейбница для форм d(x y) = dx y + (−1)degxx dy,

и то, что X C2, нетрудно показать, что d(dxI(y)) = 0.

Тема 3. Интегрирование дифференциальных форм

Лекция 8 ´

Ориентируемость многообразий

Определение ориентируемого многообразия. Ориентируемость. Условие ориентируемости RPn. Ориентируемость произвольного комплексно аналитического многообразия. Условие ориентируемости в терминах дифференциальных форм.

1. Определение ориентируемого многообразия

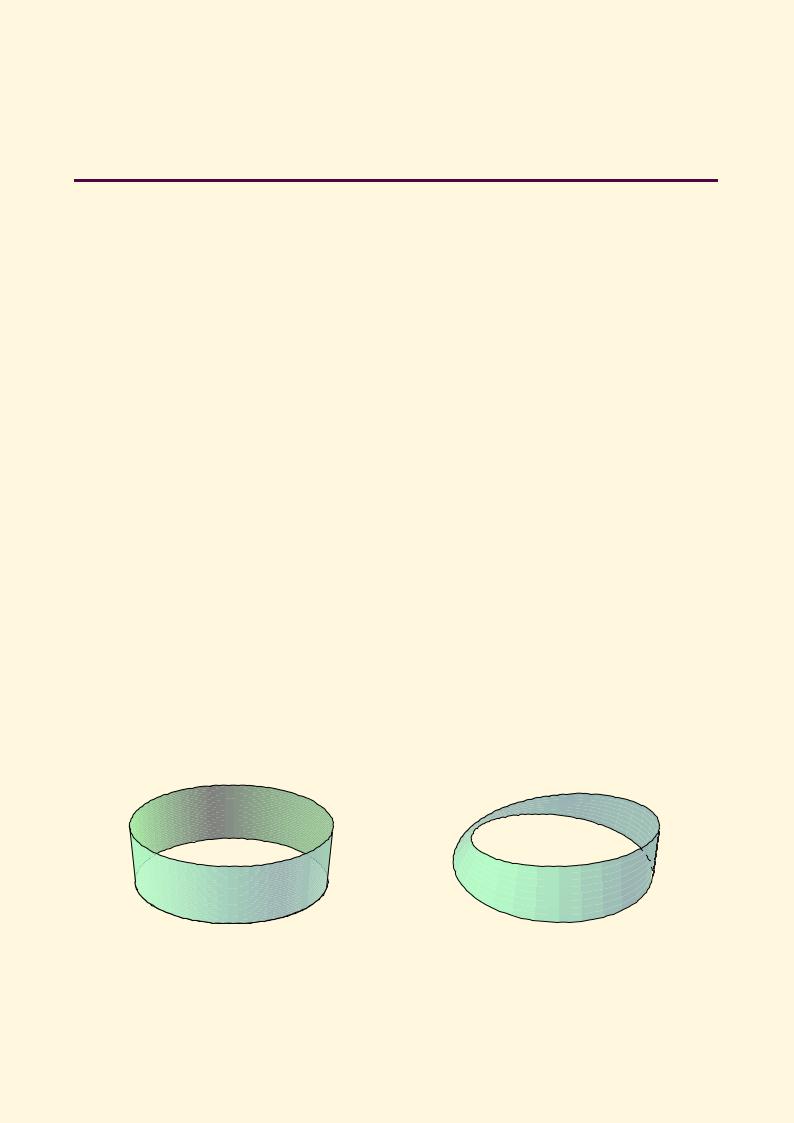
Обычно свойство ориентируемости поверхностей в R3 понимают следующим образом: если вектор нормали при обходе по любому замкнутому пути возвращается в исходное положение, то многообразие называется ориентируемым. В противном случае — неориентируемым. Согласно этому определению, цилиндр является ориентируемым многообразием, а лист Мебиуса — неориентируемым.

Цилиндр

лист Мебиуса

Такое понятие ориентируемости на языке нормалей к поверхности невозможно применить в случае абстрактного многообразия, не вложенного в евклидово пространство.

∆ Кратное интегрирование. Когомологии

73

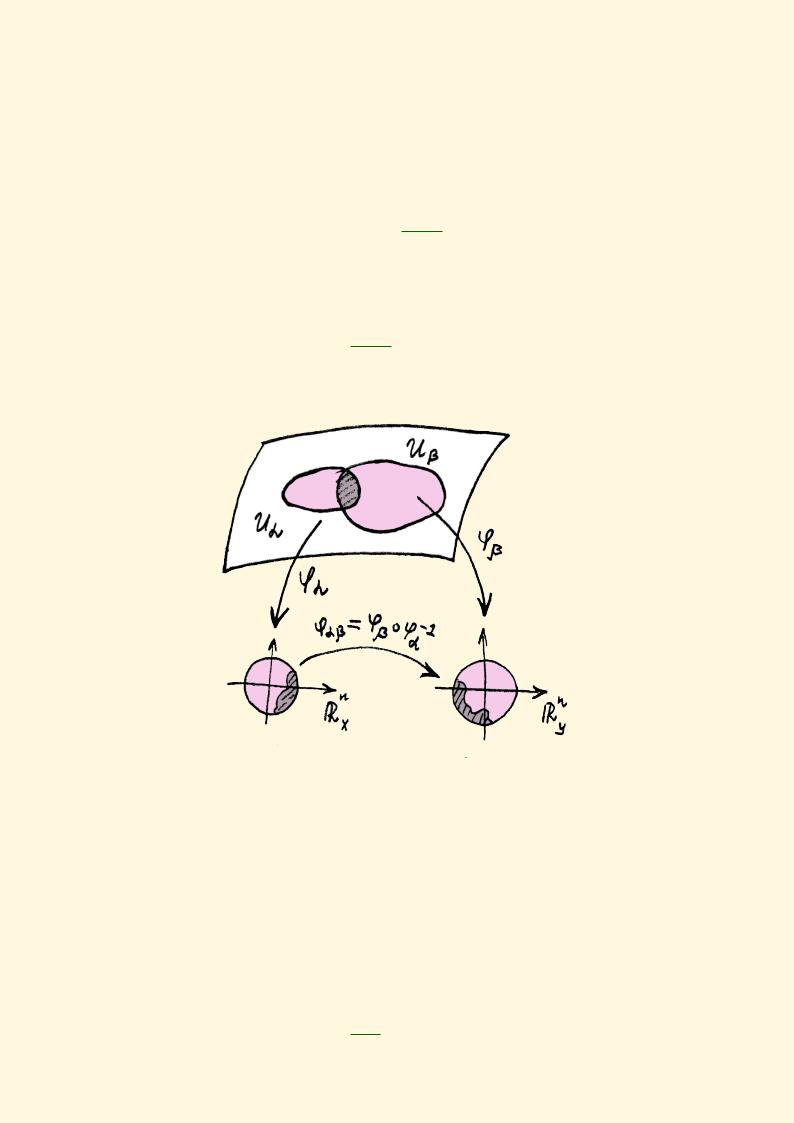
Определение 8.1. Гладкое многообразие X называется ориентируемым, если его можно покрыть семейством координатных окрестностей {Uα}

и выбрать локальные координаты в каждом Uα так, что если Uα ∩Uβ ̸=

, то якобиан перехода

Jαβ(x) = ∂ϕ∂xαβ > 0

в ϕα (Uα ∩ Uβ).

Если же нельзя осуществить указанное покрытие и выбор локальных координат так, чтобы Jαβ(x) = ∂ϕ∂xαβ > 0 для любых α, β, то многообразие называется неориентируемым.

Пример 8.1. Вещественное проективное пространство RPn ориентируемо для нечетных n.

Доказательство. Напомним, что RPn =

n

Ui, где Ui = {[ξ] : ξi ̸= 0}, при-

чем координатные отображения

=0

iS

ϕi : [ξ] Ui → x = (x1, . . . , xn) Rn

осуществляются по правилу:

x1 =

ξ0

, . . . , xi =

ξi−1

, xi+1 =

ξi+1

, . . . , xn =

ξn

.

ξ

i

ξ

i

ξ

i

ξ

i

74	И.А. Антипова, О.В. Знаменская, А.К. Цих ∆
Пусть Ui	= {[ξ] : ξi ̸= 0} и Uj = {[ξ] : ξj ̸= 0} — две координатных

окрестности. Предположим для определенности, что i < j, в Ui действуют локальные координаты x = (x1, . . . , xn), а в Uj— локальные координаты

y = (y1, . . . , yn).

Тогда функции перехода ϕij будут иметь вид:

y1 =

x1

, . . . , yi

=

xi

, yi+1 =

1

, yi+2

=

xi+1

, . . . ,

xj

xj

xj

xj

. . . , yj

=

xj−1

, yj+1

=

xj+1

, . . . , yn =

xn

.

xj

xj

xj

Вычисления показывают, что якобиан отображения ϕij равен:

ij =

1

j−1

1

1

n−j =

(−1)n

.

J

xj

· −xj2 ! · xj

xjn+1

Таким образом, если n — нечетное, то знак Jij сохраняется, но отрицателен. В противном случае знак якобиана вообще не сохраняется. Заменив в функциях перехода знаки первых координат на минусы, получим, что якобиан положителен и значит многообразие RPn для нечетных n ориентируемо.

2. Ориентируемость комплексных аналитических многообразий

Пример 8.2. Всякое комплексное аналитическое многообразие ориентируемо.

Доказательство. Напомним, что X — комплексное аналитическое многообразие, если для любой p X существует окрестность U(p), гомеоморфная шару B Cn, и при этом все функции перехода w = ϕαβ(z)

голоморфны.

Очевидно, достаточно доказать, что любое биголоморфное отображение w : Cnz → Cnw имеет положительный якобиан.

На пространство Cnz переменных zj = xj + iyj, j = 1, . . . , n можно смотреть как на вещественное пространство R2n переменных z, x, а на пространство Cnw переменных wj = uj +ivj, j = 1, . . . , n — как на вещественное пространство R2n переменных u, v.

∆ Кратное интегрирование. Когомологии

75

Отображение w = f(z) имеет вид

wk = fk(z1, . . . , zn), k = 1, . . . , n.

Оно голоморфно, т.е. все fk — голоморфные функции от z и равносильно вещественному отображению (u, v) : R2n → R2n:

( vk = vk(x1, y1, . . . , xn, yn),	k = 1, . . . , n.
uk = uk(x1, y1, . . . , xn, yn)

Представим последнее отображение как композицию отображений

	B	Φ				B−1
			w = f(z), w¯ = f(z)
	(x, y) → (z, z¯) →					→ (u, v),

где

(z, z¯) = (z1, . . . , zn, z¯1, . . . , z¯n), (w, w¯) = (w1, . . . , wn, w¯1, . . . , w¯n),

а

B−1 ◦ Φ ◦ B : (x, y) → (u, v)

— линейное преобразование и вычислим якобиан:

∂(u, v)

=

∂(B−1 ◦ Φ ◦ B)

=

B−1

∂Φ

B

=

∂Φ

.

|

|∂(z, z¯)

|

|

∂(x, y)

∂(x, y)

∂(z, z¯)

Последний якобиан

∂Φ

∂f

0

=

∂f

2

∂(z, z¯) =

0

∂f∂z

∂z

> 0,

∂z

поскольку исходное

отображение

биголоморфно

и его

якобиан отличен

от 0.

= Jαβ(xα).

76	И.А. Антипова, О.В. Знаменская, А.К. Цих ∆

3. Ориентируемость на языке дифференциальных форм

Предложение 8.1. Гладкое вещественное n-мерное многообразие ориентируемо тогда и только тогда, когда на X существует непрерывная форма ω степени n, нигде не равная нулю.

Доказательство. Докажем, что если на X существует нигде не обращающаяся в 0 форма ω степени n, то X — ориентируемо.

Пусть Uα, α A — покрывающие X координатные окрестности, а xα1 , . . . , xαn — локальные координаты в Uα. Так как ω — форма степени n, то в координатной окрестности Uα она представляется в виде

ω = ω(xα) = aα(xα)dxα1 · · · xαn.

Для координатной окрестности Uβ, аналогично, имеем:

ω = ω(xβ) = aα(xβ)dxβ1 · · · xβn.

При этом

aα(xα)dxα1 · · · xαn = aβ(xβ(xα))Jαβ dxα1 · · · xαn,

откуда

aα(xα) aβ(xβ(xα))

Пусть окрестность связная. Поскольку ω ̸= 0, функция aα на связном множестве не обращается в 0, и значит не меняет знак. Таким образом, aα либо везде больше нуля, либо везде меньше нуля. В последнем случае переставим xk с xk+1 и получим dxk xk+1 = −dxk+1 dxk. Итак, все aα > 0

и значит Jαβ > 0.
Пусть теперь X — ориентируемо, т.е. существует покрытие X =				Uα,
	J			α A
где Uα — координатные окрестности,		αβ(x) > 0 в области	определения.
				S

Построим дифференциальную форму ω степени n, нигде не равную нулю. Возьмем набор дифференциальных форм

ωα = dxα1 · · · xαn, α A.

∆ Кратное интегрирование. Когомологии

77

Рассмотрим разбиение единицы {ρα}, подчиненное покрытию Uα, т.е. набор гладких неотрицательных функций ρα : X → R, таких, что Supp ρα Uα,

глобально	P		X	ω	ω =	ραωα
α A и	α A	ρα(p) = 1, где p		— текущая точка многообразия X. Искомая,
						P
	определенная на			форма , будет иметь вид:			.

α A

Рассмотрим вопрос о придании ориентации многообразию. Пусть U —

координатная окрестность многообразия X. Задать ориентацию в окрестности U — значит выбрать в ней определенную систему локальных координат x = (x1, . . . , xn); при этом считается, что всякая другая система локальных координат y = (y1, . . . , yn) задает ту же самую ориентацию, если якобиан

перехода ∂x∂y > 0.

В случае ориентируемого многообразия задание ориентации в любой окрестности автоматически определяет ориентацию на всем многообразии, поскольку для таких многообразий функции перехода имеют положительные якобианы.

Определение 8.2 (другое определение ориентации многообразия). Пусть

X — связное ориентируемое многообразие и ω — дифференциальная форма степени n на X, непрерывная и не равная нулю всюду на X. Говорят, что ориентация на многообразии X определяется условием положительности формы ω, если эта ориентация определяется набо-

ром локальных координат xα = (xα1 , . . . , xαn), в которых ω = ω(xα) = a(xα)dxα1 · · · xαn с непрерывной функцией a(xα) > 0.

Пример 8.3. Рассмотрим окружность S1 = {x = (x1, x2) R2 : x21 + x22 = 1} и заданную на ней форму ω, которая в координатах объемлющего пространства определяеется как ω = x1dx2 − x2dx1. В локальных координатах

ϕ (в которых x1 = cos ϕ, x2 = sin ϕ) имеем ω = ω(ϕ) = cos2 ϕdϕ+sin2 ϕdϕ = dϕ, следовательно, ориентация S1, выбранная условием положительности формы ω, определяется локальной координатой ϕ.

78	И.А. Антипова, О.В. Знаменская, А.К. Цих ∆

Лекция 9 ´

Интеграл дифференциальной формы по ориентируемому многообразию

Многообразия с краем: определение, примеры, индуциро-

ванная ориентация на крае. Интеграл дифференциальной

формы по ориентируемому многообразию (с краем).

1. Определение интеграла дифференциальной формы

Наша ближайшая задача — определить интеграл дифференциальной формы корректно, т.е. согласованно с понятием ориентируемого многообразия и понятием интеграла Римана.

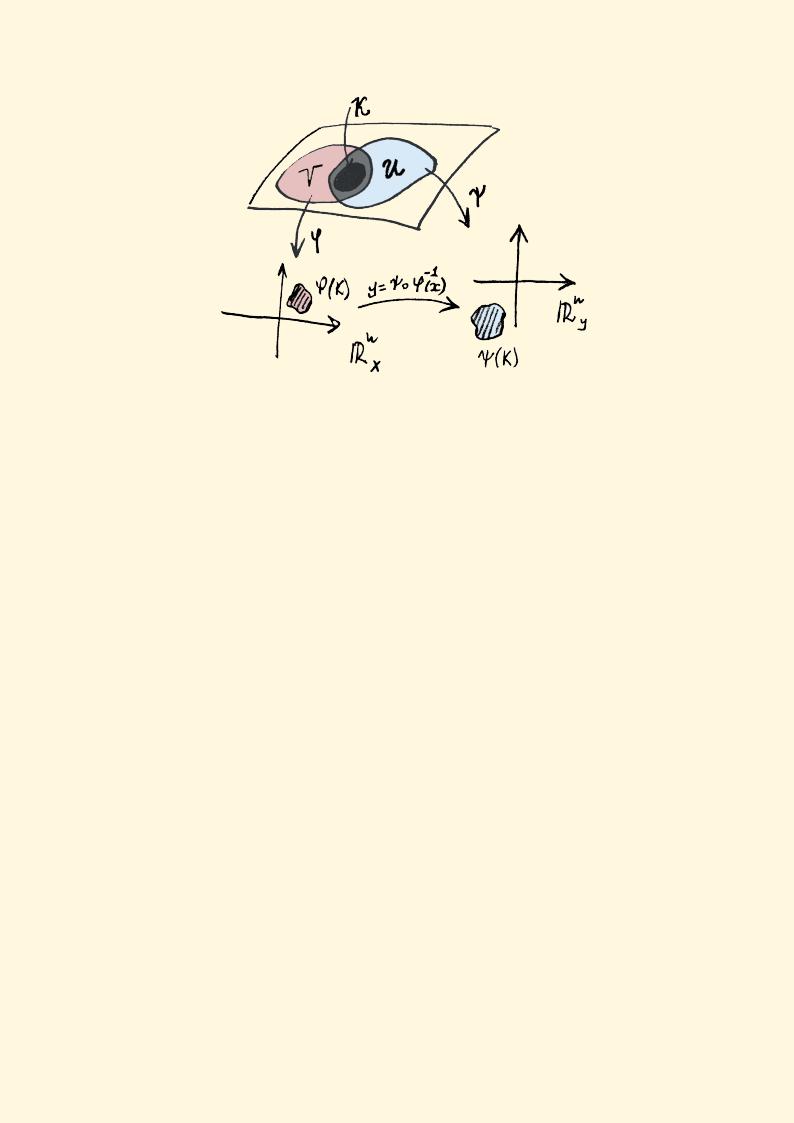
Пусть X — гладкое многообразие размерности n,

ω= a(x)dx1 · · · dxn

—форма степени n на X, функция a(x) непрерывна в U. Если K — компакт в окрестности U, естественно дать следующее определение:

Z	ω = Z	a(x)dx1 · · · dxn :=	Z	a(x)dx1 · . . . · dxn,	(9.1)
K	K		ϕ(K)

где ϕ : U → Rn — координатная функция (т.е. x = ϕ(p)), а в правой части стоит обычный Риманов интеграл.

Итак, мы определили интеграл от n-формы с компактным носителем как интеграл Римана. Проанализируем, хорошо ли это определение. Порядок x1, . . . , xn существенен для дифференциальной формы, но не влияет на интеграл Римана. Естественно, интеграл должен быть инвариантен относительно замены переменных в U ∩ V.

Пусть K U ∩ V, где в U действуют локальные координаты x = (x1, . . . , xn), в V действуют локальные координаты y = (y1, . . . , yn).

∆ Кратное интегрирование. Когомологии

79

Тогда

ωy = ω(y) = b(y)dy1 · · · dyn,

где b(y) — гладкая функция в V.

С одной стороны интеграл по компакту от формы ω равен:

				Z		Z			(9.2)
					ω =	b(y)dy1 · . . . · dyn,
				K		ψ(K)
с другой стороны:							Z	a(x)dx1 · . . . · dxn,
Z	ω =	Z	b (y(x)) ∂x(x)dx1 · . . . · dxn =						(9.3)
				∂y
K		ϕ(K)					ϕ(K)

поскольку есть правило преобразования дифференциальной формы при пе-

реходе к другой локальной карте.
Из (9.2) и (9.2) получаем равенства
Z	b(y)dy1 · . . . · dyn =	Z	b (y(x)) ∂x(x)dx1 · . . . · dxn =
				∂y
ψ(K)		ϕ(K)				Z
			=				a(x)dx1 · . . . · dxn.
						ϕ(K)

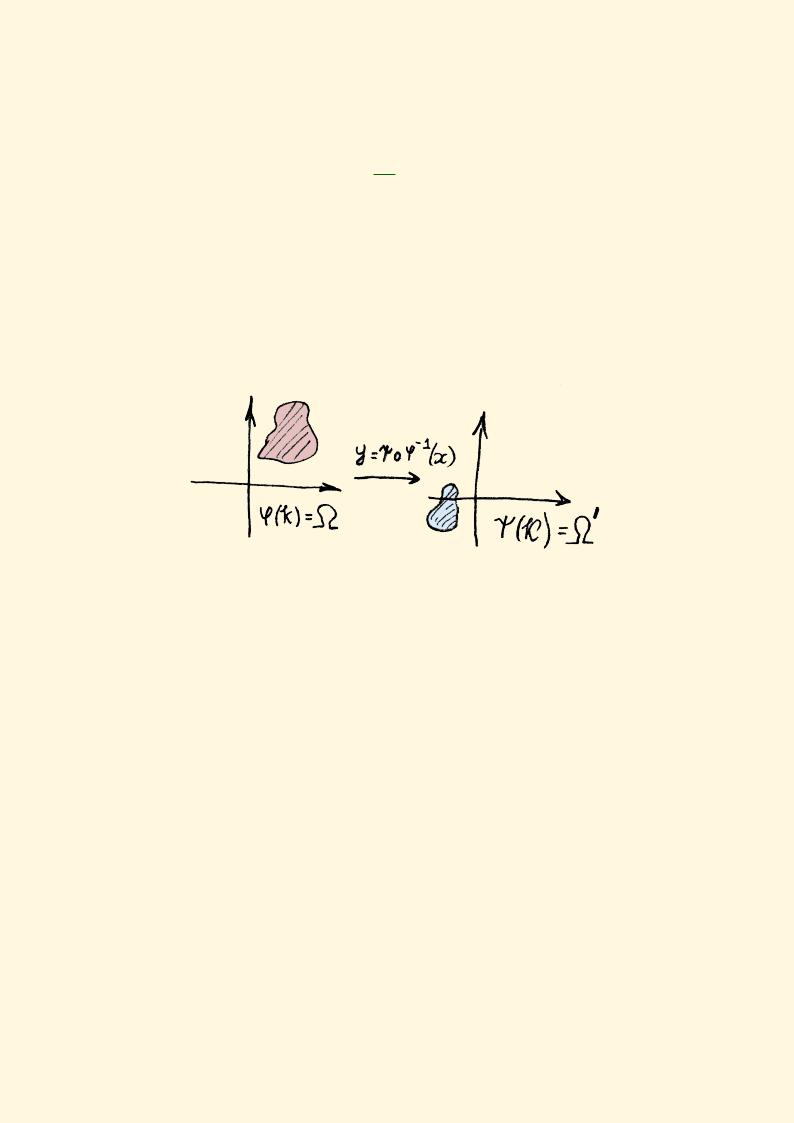
Если сделать замену переменных в интеграле

Z

f(x)dx1 · . . . · dxn,

Ω

80	И.А. Антипова, О.В. Знаменская, А.К. Цих ∆

по известному из анализа правилу замены переменных в кратных интегралах, то получим

Z

∂x

f (x(t)) dt1 · . . . · dtn,

∂t

Ω′

т.е., что домножение происходит на модуль Якобиана. Согласно же нашему определению, при переходе к другой локальной карте форма умножается на сам якобиан. Отсюда ясно, что корректность (9.1) будет обеспечена, если многообразие X ориентируемо, т.е. если ∂x∂y > 0. В противном случае определение некорректно.

Замечание 9.1. Мы могли бы рассматривать так называемые нечетные формы, которые при замене переменных умножаются на ∂x∂y . Они приспособлены для интегрирования по неориентируемым многообразиям.

Итак, пусть K — произвольный компакт на гладком ориентируемом многообразии X, {Uα} — покрытие X локальными картами. Определим интеграл по K от ω при помощи разбиения единицы. Напомним, что разбиением единицы, подчиненным покрытию {Uα}, называется семейство

{ρα} неотрицательных гладких функций на X, таких, что supp ρα Uα и

P

ρα(p) = 1 для любой p X.

Определение 9.1. Интегралом непрерывной формы ω на ориентируемом многообразии X по K называется величина

K		XK Ui			K Ui
Z	ω =	i	Z	ρiω, где	Z	ρiω	определен в (9.1),	(9.4)
			∩		∩

а {ρi} — разбиение единицы, подчиненное покрытию {Ui}.