
Сеньків М.Т. Векторний і тензорний аналіз: Текст лекцій – Львів: Ред. – видавн. Відділ Львів ун-ту. 1990 – 146 с.
У даних текстах лекцій висвітлені основи векторного і тензорного аналізу. Викладений матеріал охоплює частину програми курсу “Векторний і тензорний аналіз” .
Для студентів другого курсу фізичного факультету
Іл. : 84. Бібл. 13 назв.
В данных текстах лекций освещены основы векторного и тензорного анализа. Изложенный материал охватывает часть прогорамы курса “Векторный и тензорный анализ” .
Для студентов второго курса физического факультета.
Ил. : 84 Библ. 13 назв.
Рецензенти: акад. І.Р.Юхновський,
доц. Б.Т.Бабій
Львівський університет ім. І.Франка
В С Т У П
Дані тексти лекцій є стислим викладом, що читалися нами протягом багатьох років для студентів фізичного і математичного факультетів Львівського державного університету ім. І.Франка.
Література з векторного і тензорного аналізу обширна. Нажаль, більшість наявних посібників і монографій важко доступні для студентів другого курсу через недостатню їх математичну підготовленість. Це заставило нас розробити курс, рівень якого відповідав би програмі з математики для фізичних спеціальностей. Разом з тим, що важливо, ми намагалися наближити наш курс до курсу теоретичної фізики, який читається для студентів-фізиків. Даний курс можна розглядати як вступ до ріманової геометрії і загального тензорного аналізу, які є розділами курсу загальної теорії відносності.
Виклад матеріалу і запис формул у текстах лекцій дещо “старомодний”. Ми свідомо відмовилися від правил запису сум за Енштейном, розуміючи як важко звикатися з цим правилом. Разом з тим цікаво було глянути на добре знайомі формули в їх більш строгому, хоч і більш громіздкому записі.
Останні лекції конспекта розраховані на студентів старших курсів. Познайомившись з коваріантним диференціюванням і тензором кривизни / 34-42 / студент може приступати до вивчення загальної теорії відносності і релятивістської космології.
-4-
ВЕКТОРНИЙ АНАЛІЗ
Перед людиною три шляхи до пізнання:
шлях мислення – найбільш благородний, шлях наслідування – найбільш легкий і шлях особистого досвіду – найбільш важкий.
Конфуцій
Перетворення прямокутних координат точки
Однією з найпростіших систем координат є декартова прямокутна система координат, що визначається трьома взаємно перпендикулярними осями х, у, z. Якщо вісь z напрямити
 вертикально
вверх, то існуватимуть дві можливості
вибору осей х та у. Якщо з вершини осі z
найкоротший поворот осі х відбувається
за годинниковою стрілкою, система
називається лівою /рис.1/, проти годинникової
стрілки – правою /рис.2/. Легко бачити,
що права система координат є дзеркальним
відображенням лівої і навпаки. Далі ми
можемо використовувати ліву систему
координат.
вертикально
вверх, то існуватимуть дві можливості
вибору осей х та у. Якщо з вершини осі z
найкоротший поворот осі х відбувається
за годинниковою стрілкою, система
називається лівою /рис.1/, проти годинникової
стрілки – правою /рис.2/. Легко бачити,
що права система координат є дзеркальним
відображенням лівої і навпаки. Далі ми
можемо використовувати ліву систему
координат.
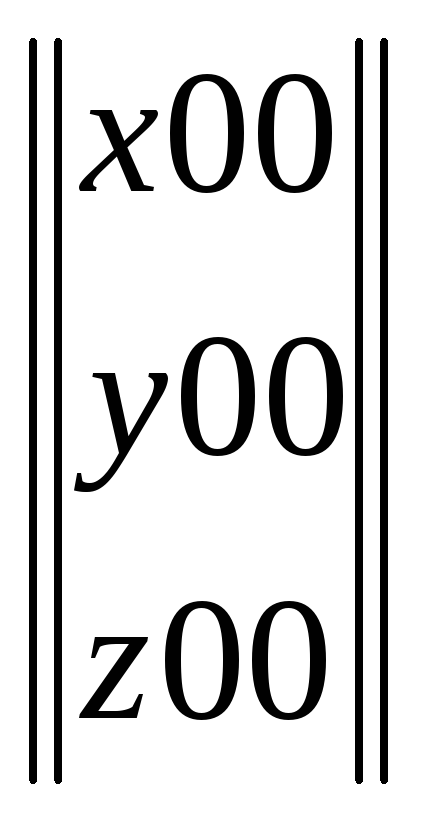
Положення точки М у системі координат Охуz визначається трьома числами х, у, z (абсциса, координата і апліката). Положення тієї ж точки можна також визначити вектором ОМ = r (радіус-вектор точки М). Якщо вести одиничні вектори ί, j, к, що визначають напрям осей х, у, z, то
![]() , (1.1)
, (1.1)
причому
![]() (1.2)
(1.2)
При переході до іншої /нової/ системи координат координати точки змінюються.
Нехай осі нової системи О'х'у'z' паралельні до осей х, у, z координати точки О' відносно систем хуz в х, у, z. Тоді, як легко бачити з рисунка 4.
-5-
 х
= х'+х
х
= х'+х
у = у'+у /1.3/
z = z'+z
У більш складному випадку, коли початки старої і нової системи збігаються, а осі утворюють кути, координати точки зв’язані лінійними співвідношеннями.
х = а11 х'+а12у'+ а13z'
у = а21 х'+а22у'+ а23z' /1.4/
z = а31 х'+а32у'+ а33z'
 Навпаки
нові координати точки виражаються через
старі формули.
Навпаки
нові координати точки виражаються через
старі формули.
х' = а11 х+а12у+ а13z
у' = а21 х+а22у+ а23z /1.5/
z' = а31 х+а32у+ а33z
Коефіцієнти аік визначають матрицю
аік =
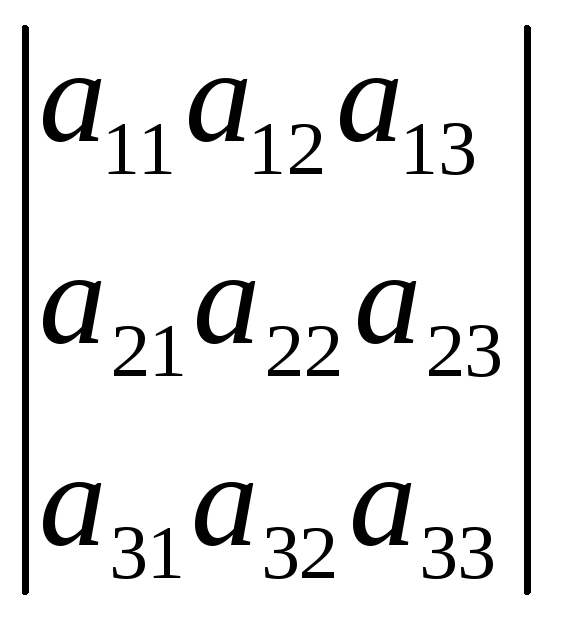 /1.6/
/1.6/
і вони мають простий геометричний зміст: це косинуси кутів між відповідними осями старої і нової системи координат.
а11 = cos(хˆх') а12 = cos(xˆy') а13=cos(xˆz'), …
Формули /1.4/ і /1.5/ можна записати компактніше, якщо вести нові позначення для координат і осей. Позначимо
х=х1 у=х2 z=х3
тоді
хі = ∑ аік х'к і=1,2,3 /1.7/
к
х'к = ∑ аік хі к=1,2,3 /1.8/
і
аік = cos(xiˆx'к) і,к=1,2,3 /1.9/
Легко переконатися, що дев’ять косинусів аік не є незалежними величинами. Відаль r точки М від початку координати можна записати
r2=x2+y2+z2,
а також
r2=x'2+у'2+z'2,
Отже,
x2+y2+z2= x'2+у'2+z'2,
∑ х2і = ∑ х'2к.
-6-
Підставимо сюди / 1.7 /
∑ ( ∑ аік х'к )2 = ∑ х'2к
і к к
Квадрат суми можна записати як подвійну суму
( ∑ Ак )2 = ∑ ∑ Ак Аl
к к А
і також
( ∑ аік х'к )2 = ∑ ∑ аік аіl х'к х'l
к і
Тому
∑ ∑ ∑ аік аіl х'к х'l = ∑ х'2к
і к l к
У лівій стороні цієї рівності маємо 27 доданків, у правій – три. Рівності збігаються, якщо
∑ аік аіl = δкl = {
і
де δкl – символ Кронекера. Дійсно, тоді
∑ ∑ δкl х'к х'l = ∑ х'2
к і к
Остання рівність є прикладом на застосування так званого правила підстановки індекса: якщо під знаком суми стоїть символ Кронекера, то ми можемо відкинути символ суми / в нашому нашому випадку по індексу l / і сам символ Кронекера, а у виразі, що залишився, індекс, за яким велось сумування, змінюємо на індекс символа Кронекера. Взагалі,
∑ δік А..і.. = А..к..
і
Рівність /1.10/ виражає шість умов, якими зв’язані косинуси аік. Наприклад, при к=l=1 одержимо
∑ аі1 аі1 = 1 , а211+а221+а231 = 1
і
При к=1, l=2 / або ж при к=2, l=1 /
∑ аі1 аі2 = 0, а11а12+а21а22+а31а32 = 0
і
Всі шість умов мають вигляд
а211+а221+а231 = 1 а11а12+а21а22+а31а32 = 0
а212+а222+а232 = 1 а12а13+а22а23+а32а33 = 0 /1.11/
а213+а223+а232 = 1 а13а11+а23а21+а33а31 = 0
-7-
Перші три рівності – це запис теореми Піфагора в тригонометричній формі. Решта три рівності – це умови перпендикулярності координатних осей. Наприклад, /1.11/ є умовою перпендикулярності осей у' і z'
cos(xˆy') cos(xˆz') + cos(yˆy') cos(yˆz') + cos(zˆy') cos(zˆz') = 0
Формули /1.10/ і /1.11/ показують, що з дев’яти косинусів незалежними є тільки три.
Співвідношення /1.10/ ми одержали підставляючи в рівність
∑ х2і = ∑ х'2к
вираз /1.7/ для хі. Якщо ж в цю рівність підставити вираз /1.8/ для х'к
∑ х2і = ∑(∑ аік хі)2 = ∑∑∑ аік аlк хк хl,
і к і і к l
то звідси випливає, що
∑ аік аlк = δіl /1.12/
к
Ми одержали шість нових умов для косинусів
а212+а212+а213 = 1 а11а21+а12а22+а13а23 = 0
а221+а222+а223 = 1 а21а31+а22а32+а23а33 = 0 /1.13/
а231+а232+а233 = 1 а31а11+а32а22+а33а23 = 0
Ці формули, однак, є наслідком з умов /1.10/ і тому використовувати треба або /1.10/ або /1.12/.
Формули перетворення координат /1.4/ і /1.5/ можна записати символічно
х = ах',
х' = атх.
Розглядаючи х і х' як матриці
Х =
 ,х' =
,х' =
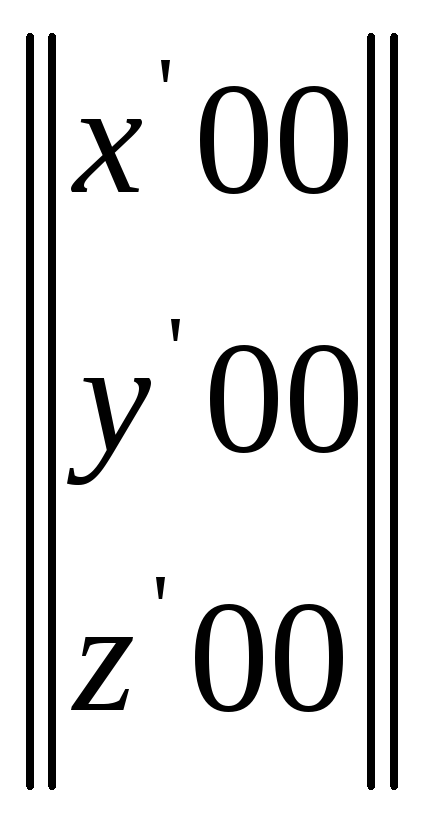 ,
,
де а – матриця з коефіцієнтів
![]() ;
;![]() - транспонована матриця.
- транспонована матриця.
Дійсно,
-8-
Ця матрична рівність еквівалентна формулам /1.4/. Аналогічно доводиться, що рівність /1.15/ еквівалентна /1.5/.
Ознайомимось з особливим перетворенням координат – перетворенням інверсії. Перетворенням інверсії називається дзеркальне відображення однієї або трьох осей.
У випадку дзеркального відображення однієї осі х /рис.6/ маємо

![]() ,
,
![]() , /1.16/
, /1.16/
![]() .
.
у випадку дзеркального відображення трьох осей
![]() ,
,
![]() , /1.17/
, /1.17/
![]() ,
,
Легко бачити, що формули /1.16/ і /1.17/ є частинним випадком перетворення /1.4/ ; коефіцієнти аік відповідно
 визначають
матриці
визначають
матриці
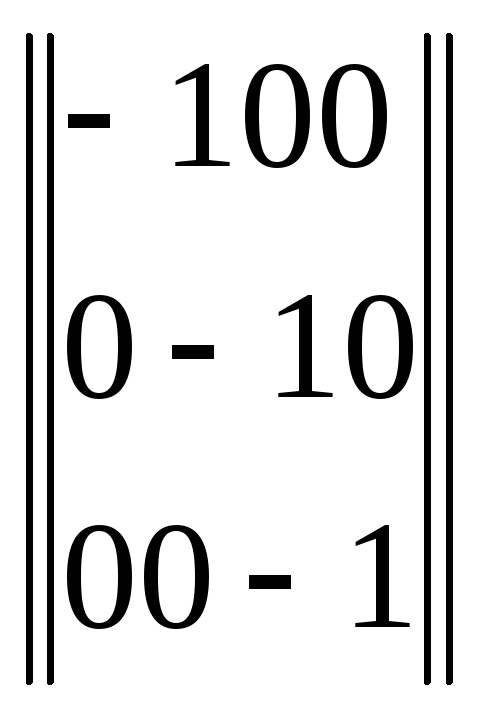
аік = 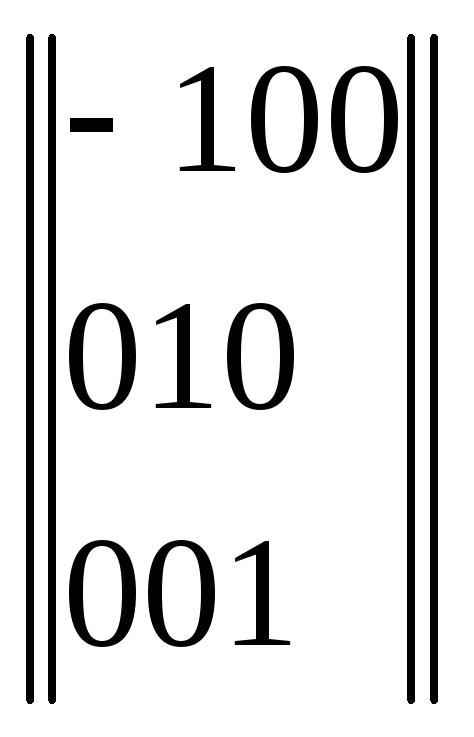 аік
=
аік
=
Очевидно і в цьому випадку задовольняються умови /1.10/ або /1.12/.
Перетворення інверсії – це
перехід від лівої системи до правої і
навпаки. Воно є прикладом так званих
дискретних перетворень: його не можна
здійснити з допомогою суми нескінченно
малих поворотів системи Охуz навколо
точки О. зауважимо, що дзеркальне
відображення двох осей не є перетворенням
інверсії. Його можна одержати як результат
повороту системи Охуz навколо однієї з
осей на кут 180![]() .
.
Доведемо важливу теорему.
Квадрат детермінанта, побудованого з коефіцієнтів довільного
-9-
перетворення координат, дорівнює одиниці.
Доведення. Розглянемо довільне перетворення координат /поворот або інверсію/. Тоді
Хі =
![]() ,
,
![]() .
.
Побудуємо детермінант від обох сторін останньої рівності
 =1
=1
і введемо позначення
![]()
Тоді
![]() = 1
= 1
Згідно з відомим правилом
множення детермінантів ліва сторона
рівності – добуток двох детермінантів
/
![]() / і /
/ і /![]() /. Обидва множники в лівій стороні
однакові / значення детермінантів не
змінюється, якщо переставити рядки зі
стовбцями /.Отже
/. Обидва множники в лівій стороні
однакові / значення детермінантів не
змінюється, якщо переставити рядки зі
стовбцями /.Отже
![]()
і тому
![]() . /1.18/
. /1.18/
Значення +1 відповідає власним поворотам координатної системи, значення -1 – інверсії чичтеми.
На закінчення цього параграфа наведемо важливий приклад з механіки.
Розглянемо тверде тіло, що
має нерухому точку О. З тілом зв’яжемо
систему
![]() ,
стосовно якого тіло нерухоме. Рух тіла
будемо вивчати стосовно абсолютної
системи
,
стосовно якого тіло нерухоме. Рух тіла
будемо вивчати стосовно абсолютної
системи![]() .
Положення тіла /а значить і системи
.
Положення тіла /а значить і системи![]() /
по відношенні до абсолютної системи
визначається дев’ятьма косинусами
/
по відношенні до абсолютної системи
визначається дев’ятьма косинусами![]() . Однак, незалежних косинусів, а значить
і кутів, є три.
. Однак, незалежних косинусів, а значить
і кутів, є три.
-10-
сів, а значить і кутів , є три. Цим і підтверджується відомий факт, що тверде тіло з однією нерухомою точкою має три ступені вільності. У зв’язку з цим замість дев’яти величин аік зручно вибирати три незалежні кути φ,ψ і δ / кут власного обертання, кут процесії і кут нотації/. Ці кути одночасно визначають положення твердого тіла відносно абсолютної системи, а в випадку руху тіла
φ=φ(t), ψ=ψ(t), δ=δ(t).
Люди, що засвоїли
великі принципи математики
мають на один орган чуття
більше, ніж прості смертні.
Ч.Дарвін
2. Перетворення компонент вектора при переході від однієї прямокутної
системи до іншої.
Вектором називається величина, характеризована числом, що визначає її в певних одиницях міри, а також своїм напрямком у просторі. Числове значення вектора називається модулем або довжиною вектора.
Розрізняють вектори трьох видів: вільні, пересувні /ковзні/ і означені /закріплені/. Прикладом вільного вектора є вектор кутової швидкості, вектор моменту сили. Прикладом пересувного вектора є вектор сили. З означеним вектором зустрічаємось в механіці деформованого середовища /вектор деформації/.
Вектори будемо позначати великими латинськими буквами А,В,С,…
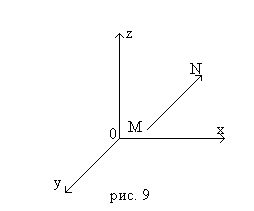 У прямокутній системі координат
вектор А визначається трьома компонентами
/проекціями/
У прямокутній системі координат
вектор А визначається трьома компонентами
/проекціями/
Ах, Ау, Аz. При цьому
А=Ахі + Ауj + Аzk, /2.1/
А=√А2х + А2у + А2z. /2.2/
Кути, що їх утворює вектор А з координатними осями, визначається за допомогою
косинусів
cos(Ax)= Ax/А, cos(Ay)= Ay/A, cos(Az)= Az/A /2.3/
координати точок М і N початку і кінця вектора А позначимо
-11-
через Хм, Ум, Zм і Xn, Уn, Zn, тоді
Ах = Хn-Xм, Ау = Уn-Ум, Аz = Zn-Zм.
Звідси зрозуміло, що при переході до нової системи координат компоненти вектора перетворюються за тим же законом, що й координати
Аі = ∑ аікА'к і=1,2,3 /2.4/
к
А'к= ∑ аікАі к=1,2,3 /2.5/
і
де аік – відомі косинуси, що задовольняють умові /1.10/ або /1.11/. Зокрема, при перетворенні інверсії, коли
компоненти вектора повинні перетворюватися за законом
Ах = -А'х Ау = А'у Аz = A'z
Приклад. Нехай відомі компоненти вектора АхАу у системі координат на площині.
В ведемо
полярну систему ( r, φ ). Проекцію вектора
А на радіус-вектор будемо називати
радіальною компонентою Аr, проекцію на
нормаль до радіуса-вектора трансверсальною
/ поперечною / компонентою Аφ. Знайдемо
залежність між Ах,Ау з одного боку і Аr,
Аφ з другого.
ведемо
полярну систему ( r, φ ). Проекцію вектора
А на радіус-вектор будемо називати
радіальною компонентою Аr, проекцію на
нормаль до радіуса-вектора трансверсальною
/ поперечною / компонентою Аφ. Знайдемо
залежність між Ах,Ау з одного боку і Аr,
Аφ з другого.
З рис.10 маємо
а11 = cos ( xˆx' )= cosφ
a12= cos ( xˆy' )= cos (90˚+φ) = -sinφ
a21= cos ( yˆx' )= sinφ
a22= cos ( yˆy' )= cosφ
Згідно з /2.4/ і /2.5/ відразу знайдемо
Ax = Ar cosφ – Aφ sinφ ,
Ay = Ar sinφ + Aφ cosφ ,
Ar = Ax cosφ – Ay sinφ ,
Aφ = -Ax sinφ + Ay cosφ .
-12-
На цілому світі все
здійснюється по математичному.
Г.Лейбніц
3. Елементи векторної алгебри.
Нагадаємо коротко основні алгебраїчні дії над векторами.
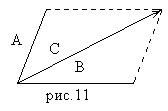 Сумою
двох векторів А і В називаємо третій
вектор С, який одержують як діагональ
паралелограма, побудованого на векторах
А і В.
Сумою
двох векторів А і В називаємо третій
вектор С, який одержують як діагональ
паралелограма, побудованого на векторах
А і В.
С = А + В. /3.1/
Така сума називається геометричною.
Різниця двох векторів А і В можна звести до суми двох
в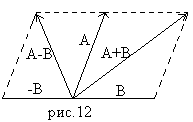 екторів
А і –В
екторів
А і –В
А – В = А + (-В),
де вектор –В відрізняється від вектора В тільки напрямком.
Легко бачити, що в паралелограмі, побудованому на векторах А і В, одна діагональ є сумою
С = А + В,
а друга – різницею
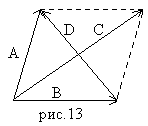 D = А – В. /3.2/
D = А – В. /3.2/
Формули /3.1/ і /3.2/ можна спроектувати на координатні осі. Якщо
С = А ± В,
то
Ск = Ак ± Вк /3.3/
З фізичної і геометричної точки зору повинні існувати два типи добутків двох векторів: скалярний і векторний.
Скалярним добутком двох векторів А і В називається число, що дорівнює добуткові довжини обох векторів, помноженому на косинус кута між ними.
Скалярний добуток двох векторів будимо позначати (АВ) або просто АВ, отже
АВ = АВ cos (AˆB). /3.4/
З /3.4/ випливає, що скалярний добуток двох ортогональних векторів дорівнює нулеві.
-13-
AВ = 0 якщо А ┴ В,
і зокрема,
ij = jk = ki = 0 /3.5/
Квадрати ортів, згідно з /3.4/, дорівнюють одиниці
і2 = j2 = k2 = 1 /3.6/
Вектори А і В запишемо через їх компоненти
A = Axi + Ayj + Azk,
B = Bxi + Byj + Bzk,
тоді
АВ = (Axi + Ayj + Azk) (Bxi + Byj + Bzk)
Враховуючи /3.5/ і /3.6/, одержимо
АВ = АхВх + АуВу + АzBz /3.7/
або скорочено
АВ = ∑ АіВі /3.8/
і
Переконаємось, що скалярний добуток двох векторів є інваріантом, тобто не залежить від вибору системи координат.
Здійснимо перехід від системи координат хуz до системи х'у'z', причому
Хі = ∑ аік хк Аі = ∑ аікА'к
к
Хк = ∑ аік Хі Ак = ∑ аік Аі.
і
Тоді
∑ Аі Ві = ∑ ∑ ∑ аік аів А'к А'і =
і і к і
= ∑∑ ( ∑аікаів ) А'к А'в = ∑∑δкв А'к А'в.
к і і к і
Використовуючи правило підстановки індекса, остаточно маємо
∑АіВі = ∑ А'к В'к
і к
або в розгорненому вигляді
АхВх + АуВу + АzBz = А'xВ'x + А'yВ'y + А'zВ'z. /3.9/
У фізиці ми часто зустрічаємось зі скалярним множенням векторів. Наприклад, щоб порахувати роботу А сили F на шляху S ці вектори треба скалярно перемножити
А = FS = FS cos (F,S)
Іншим прикладом скалярних добутків є потужність FV /скалярний добуток сили на швидкість/ та інші величини, з якими познайомимось пізніше /лінійний інтеграл, потік вектора через поверхню, та інші/.
-14-
Введемо поняття про векторний добуток двох векторів.
Векторним добутком двох
векторів
![]() будемо називати третій вектор
будемо називати третій вектор![]() ,
що має такі властивості:
,
що має такі властивості:![]()
 1/
1/![]()
![]() ,
,
2/
![]() sin
(
sin
(![]() ).
).
3/ вектор
![]() напрямлений так, що з його кінця видно
найкоротше обертання вектора
напрямлений так, що з його кінця видно
найкоротше обертання вектора![]() у бік вектора
у бік вектора![]() у
у
напрямку годинникової стрілки.
Векторний добуток двох векторів позначемо
![]() . /3.10/
. /3.10/
З означення випливає, що векторний добуток антикумутативний
![]() ,
,
а також, що
![]() .
.
Для ортів маємо
![]()
![]()
![]()
![]() . /3.11/
. /3.11/
![]() . /3.12/
. /3.12/
Неважко знайти вираз для векторного добутку через компоненти обох множників. Якщо
![]() Ах
Ах![]() +Ау
+Ау![]() +Аz
+Аz![]() ,
,
![]() Вх
Вх![]() +Ву
+Ву![]() +Вz
+Вz![]() ,
,
То, враховуючи /3.11/ і /3.12/, після нескладних підрахунків одержемо
![]()
![]() , /3.13/
, /3.13/
тобто
![]() АуВz – AzBy,
АуВz – AzBy,
![]() AzBx – AxBz,
AzBx – AxBz,
![]() AxBy – AyBx. /3.14/
AxBy – AyBx. /3.14/
Можна навести чимало прикладів
векторних добутків двох векторів: момент
сили
![]() є векторним добутком радіус-вектора
точки її прикладання на величину сили
є векторним добутком радіус-вектора
точки її прикладання на величину сили
![]() ,
,
-15-
лінійна швидкість
![]() точки тіла, що обертається, є векторним
добутком кутової швидкості
точки тіла, що обертається, є векторним
добутком кутової швидкості![]() на
радіус-вектор цієї точки
на
радіус-вектор цієї точки
![]() ,
,
вектор Пойтінга / густина
потоку електромагнітної енергії /
дорівнює добуткові напруженостей
електричного і магнітного полів
![]()
![]() .
.
За аналогією з добутком двох векторів, можна вести поняття про добуток трьох і більше векторів.
Якщо задані три вектори
![]() то можливі три типи добутків.
то можливі три типи добутків.
1. Добуток
![]()
вектор колінеарний до вектора
 і в
і в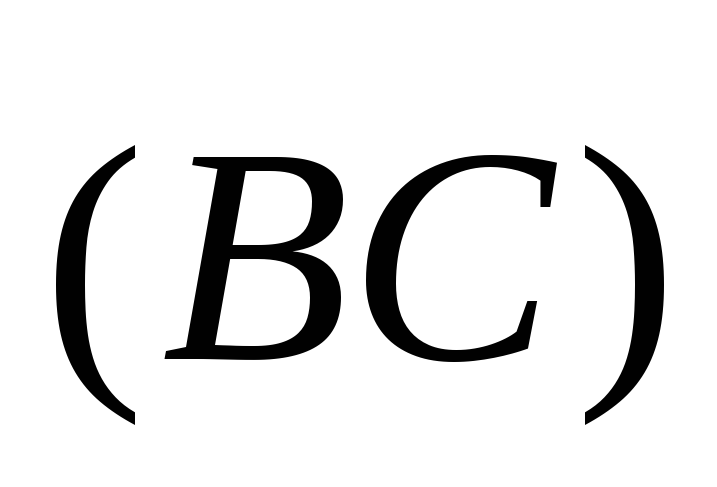 разів довший за вектор
разів довший за вектор .
.
2. Мішаний добуток трьох векторів
![]()
це скаляр, значення якого розкривається так:
![]() = Ах
= Ах![]() х
+ Ау
х
+ Ау![]() у
+ Аz
у
+ Аz![]() z
=
z
=
= Ах (ByCz – BzCy) + Аy (BzCx – BxCz) + Аz (BxCy – ByCx),
отже,
![]()
![]() =
=![]()
![]() . /3.15/
. /3.15/
У мішаному добутку трьох векторів можна циклічно переставляти множники
![]() =
=![]() . /3.16/
. /3.16/
Це випливає з відомої властивості детермінантів: значення детермінанта не змінюється, якщо здійснити циклічну перестановку його рядків.
Як відомо з аналітичної
геометрії, мішаний добуток
![]() має прямий геометричний зміст: це об’єм
паралелепіпеда, побудованого на векторах
має прямий геометричний зміст: це об’єм
паралелепіпеда, побудованого на векторах![]()
3. Подвійний векторний добуток трьох векторів
![]()
-16-
з вектором. Причому
![]() /3.17/
/3.17/
Щоб довести /3.17/ запишемо.
![]() =
=![]()
![]() .
.
і розглянемо х – компоненту цього детермінанта
![]() к
= Ау
к
= Ау![]() z - Аz
z - Аz![]() y. /3.18/
y. /3.18/
З другого боку
![]() х
= Вх(АхСх+АуСу+АzCz) – Cx(AxBx+AyBy+AzBz) =
х
= Вх(АхСх+АуСу+АzCz) – Cx(AxBx+AyBy+AzBz) =
= Ay(BxCy-ByCx) – Az(BzCx-BxCz) = Ay
![]() z
- Az
z
- Az![]() y,
y,
що збігається з /3.18/.
Безпосередньою перевіркою можна показати, що має місце така тотожність
![]() +
+![]() +
+![]() = 0. /3.19/
= 0. /3.19/
З багатьох можливих добутків чотирьох векторів запишемо тільки дві формули
![]() /3.20/
/3.20/
![]()
![]()
![]() /3.21/
/3.21/
Їх справедливість можна перевірити безпосередньо.
Як приклад добутку багатьох векторів запишемо ще / без доказу / так звану тотожність Лагранжа
![]()
(![]() =
=![]() /3.22/
/3.22/
![]()
-17-
Він знав, що одна з них була права, знав він крім цього, що якщо він вирішить, яка з них права, то ліва буде та, що залишилася. Однак він ніяк не міг згадати, з чого треба починати.
А.Мілн
4. Псевдовеличини
Розглянемо два вектори
![]() в прямокутній системі координат Охуz.
Здійснимо інверсію осі х, тоді
в прямокутній системі координат Охуz.
Здійснимо інверсію осі х, тоді
х = -х’ у = у’ z = z’ /4.1/
Компоненти вектора перетворюються за тим же законом, що й координати. Отже
Ax = -A’x Bx = -B’x
Ay = A’y By = B’y /4.2/
Az = A’z Bz = B’z
Розглянемо векторний добуток
![]()
Його компоненти в системі xyz дорівнюють
Сх = AyBz – AzBy ,
Cy = AzBx – AxBz ,
Cz = AxBy – AyBx ,
а в системі x’y’z’
C’x = A’yB’z – A’zB’y ,
C’y = A’zB’x – A’xB’z ,
C’z = A’xB’y – A’yB’x .
Підставляючи /4.2/ одержио
C’x = AyBz – AzBy = Cx
C’y = AzBx – AxBz = - Cy /4.3/
C’z = AxBy – AyBx = - Cz
Як бачимо трансформаційні
властивості вектора
![]() інші, ніж у векторів
інші, ніж у векторів![]() :
його х – компонента при перетворенні
інверсії не змінює знака, у і z – компоненти
змінюють знак на протилежний. Вектори
з такими властивостями будемо називати
/ осьовими /.
:
його х – компонента при перетворенні
інверсії не змінює знака, у і z – компоненти
змінюють знак на протилежний. Вектори
з такими властивостями будемо називати
/ осьовими /.
-18-
векторами або псевдовекторами.
Таким чином, існують два типи векторів:
1/ вектори, які при інверсії системи координат напрямку не змінюють / у нашому випадку вектори А і В /. Такі вектори називають полярними. Прикладами полярних векторів є радіус-вектор r, вектор лінійної швидкості ν, вектор сили та інші.;\
2/ вектори, які при інверсії системи змінюють напрямок на протилежний / у нашому випадку вектор С = [ AB ] /. Це так звані аксіональні вектори, або псевдовектори. Прикладом аксіональних векторів є момент сили Д = [ rF ], вектор кутової швидкості ω та інші. Зокрема, векторний добуток двох полярних векторів є псевдовектором.
При перетвореннях координат, які є перетворенням повороту системи, ніякої різниці між векторами і псевдовекторами немає. Різниця між ними з’являється тільки при перетворенні інверсії, коли вектор не змінює напрямку, а псевдовектор змінює його на протилежний.
Закон перетворення компонент вектора
Аі = ∑аік А'к /4.4/
к
у випадку перетворення повороту справджується як для вектора, так і для псевдовектора. Якщо ж врахувати і перетворення інверсії, то /4.4/ справджується тільки для векторів. Для псевдовекторів /4.4/ узагальнюється так:
Аі = Ісt |аік| ∑ аік А'к /4.5/
к
причому
Дсt | аік | = ±1
Розглянемо скалярний добуток вектора А і псевдовектора С.
У системі хуz
AC = AxCx + AyCy + AzCz,
а якщо здійснити перетворення інверсії, то
(AC)' = А'хА'у + А'уС'у + А'zC'z = - (AxCx + AyCy + AzCz)
Таким чином скалярний добуток АС при перетворенні інверсії змінює свій знак на протилежний. Скалярні величини, які при перетворенні інверсії змінюють свій знак на протилежний, називаються псевдоскалярами.
Доведена нами в попередньому параграфі теорема про інваріантність скалярного добутку /3.9/ не є універсальною: вона справджується для добутку вектора і псевдовектора при перетворенні інверсії тільки з точністю до знака.
Псевдо величини дуже важливі у теоретичній фізиці. Як з’ясувалося в основному мезонної теорії ядерних сил треба покласти величину φ, яка є псевдовектором / псевдоскалярна теорія мезонного поля /. Має історичне значення псевдовекторна теорія мезонного поля.
Задача. Довести, що добуток полярного вектора і псевдовектора є
полярним вектором.
Фрідріх Вільгельм Бессоль / 1784-1846 / народився в
місті Мінделі в Вестфалії. Пристрасть до чисел і ненависть до латинської граматики привели його до вибору комерційної професії. Бажаючи стати капітаном торгового корабля, він зацікавився теорією навігації… Успіх привів його до вивчення астрономії… Заохочений Ольберсом він покинув свої мрії про багатство і зробив вибір: бідність і зірки.
5. Вектор – функція скалярного аргумента.
Розглянуті нами алгебраїчні дії з векторами придані як для сталих, так і для змінних векторів.
Розглянемо вектор А, що є функцією аргументу t.
А = А(t)
Аргументом може бути, наприклад, час t.

Введемо координатну систему хуz. Різними значеннями аргумента t відповідають різні вектори А, як за довжиною, так і за напрямом. Геометричне місце кінці вектора А будемо називати годографом вектора А. Наприклад, годографом радіус-вектора рухомої точки А(t) буде траєкторія точки.
Розглянемо два значення аргументу t і t+Δt, де Δt – довільний приріст аргументу. При зміні аргументу на величину Δt вектор А набуває приросту ΔА.
ΔА = А(t+Δt) – А(t).
-20-
Відношення
![]() =
=![]() /5.1/
/5.1/
характеризує зміну вектора
![]() при зміні аргументу на одиницю. Цей
вираз залежить від початкового значення
аргументу
при зміні аргументу на одиницю. Цей
вираз залежить від початкового значення
аргументу![]() і від величини
і від величини![]() .
.
Щоб оцінити зміну вектора
![]() при значенні аргументу
при значенні аргументу![]() розглянемо границю
розглянемо границю
![]() lim
lim![]() = lim
= lim![]() =
=![]() . /5.2/
. /5.2/
Її називають похідною від
вектора по скалярному аргументу
![]()
Якщо врахувати, що
![]() ,
,
то
![]() . /5.3/
. /5.3/
Відомі правила диференціювання
переносяться і на вектори. Наприклад,
якщо
![]() - функції
- функції![]() ,
то
,
то
![]()
Вектор
![]() (
(![]() )
можна розкласти в ряд Тейлора
)
можна розкласти в ряд Тейлора
![]() (
(![]() )
=
)
=![]() (
(![]() 0)
+
0)
+
![]() (
(![]() 0)+
. . . /5.4/
0)+
. . . /5.4/
За аналогією з відомими поняттями з аналізу можна ввести поняття означеного і неозначеного інтеграла від вектора.
Нехай
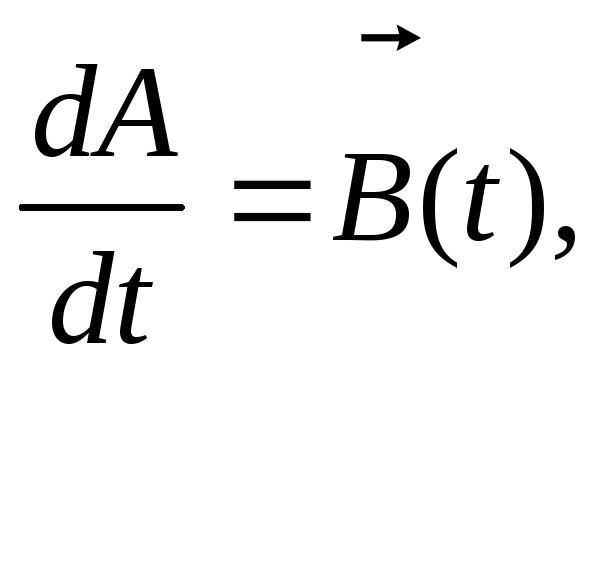
тоді
![]() /5.5/
/5.5/
тобто
![]()
Аналогічно вводиться поняття означеного інтеграла
![]()
-21-
Немає науки не зв’язаної з математикою: будь-яка наука, якщо вона має бути ґрунтовно розроблена, потребує застосування вищої математики.
Л.Ейлер
6. Скалярне і векторне поле. Градієнт скалярного поля.
Означення 1. якщо якась скалярна величина має визначене значення в кожній точці простору або частині простору, ми говоримо про скалярне поле цієї величини.
Приклад1. Поле температур. Нехай кожній точці простору з координатами х,у,z відповідає своя температура θ. У цьому випадку мова йде про поле температур.
Θ = θ( х,у,z).
Приклад 2. У просторі знаходиться речовина зі змінною густиною μ.
О бласть
простору можна розглядати як поле
густини.
бласть
простору можна розглядати як поле
густини.
μ = μ(х,у,z).
Приклад 3. Поле електростатичного потенціалу. У координатній системі хуz знаходиться система зарядів l1,l2…ln. Для того, щоб перенести одиничний додатній заряд з нескінченності в точку з координатами хуz, треба виконати роботу φ= φ(х,у,z). Цю роботу і називають потенціалом електростатичного поля.
Будемо вважати, що скалярне поле задане функцією.
φ= φ(х,у,z). /6.1/
Таке поле називають стаціонарним. Якщо φ залежить також і від часу
φ= φ(х,у,z,t),
то поле називають нестаціонарним.
Розглянемо рівняння
φ= φ(х,у,z) = С /6.2/
Воно визначає в просторі певну поверхню, яку називають поверхнею рівня. Надаючи константі С різні значення, матимемо сім’ю поверхонь рівня. Поверхні рівня не повинні перетинатися. Дійсно, на лінії перетину двох поверхонь.
-22-
![]() 1
= C1 і
1
= C1 і ![]() 2
= C2
2
= C2
функція
 мала б два різні значення, що недоступно.
Математично це означає, що функція
мала б два різні значення, що недоступно.
Математично це означає, що функція (
х,у,z ) повинна бути однозначною.
(
х,у,z ) повинна бути однозначною.
Приклад1. У випадку електростатичного поля поверхні рівня називають еквіпотенціальними поверхнями. Для поля, створеного точковим зарядом е
![]() =
=![]() і еквіпотенціальними поверхнями
і еквіпотенціальними поверхнями![]() =const
є концентричні сфери
=const
є концентричні сфери
![]()
Приклад2. Нехай задане поле
![]() =
arcsin
=
arcsin![]() .
.
Його поверхні рівня визначаються рівнянням
arcsin![]() =
С,
=
С,
![]() =
sinC =
=
sinC =![]() ,
,![]()
- сім’я кругових конусів з вершиною на початку координат.
Означення 2. Якщо якась векторна величина має визначене значення в кожній точці простору або частини простору, ми говоримо про векторне поле цієї величини:
![]() (x,y,z) /6.3/
(x,y,z) /6.3/
Векторні поля бувають стаціонарні
![]() (x,y,z)
(x,y,z)
і нестаціонарні
![]() (x,y,z,t)
(x,y,z,t)
Рівняння /6.3/ еквівалентне трьом скалярним рівнянням
Ах = Ах (x,y,z),
Ау = Ау (x,y,z), /6.4/
Аz = Az (x,y,z).
Інколи /6.3/ записують скорочено
![]() (
(![]() ) /6.5/
) /6.5/
-23-
Приклад 1. Силове поле. Якщо на масу m, поміщену в довільну точку простору
x ,y,z,
діє сила
,y,z,
діє сила
![]() (x,y,z),
(x,y,z),
То ми говоримо про векторне силове поле. Окремим випадком силового поля є гравітаційне поле, створене масою M. Якщо маса M знаходиться в початку координат, то
![]()
Приклад 2. Поле напруженостей електростатичного поля. Розглянемо систему зарядів l1,l2…ln. Тоді на
о диничний
додатній заряд, поміщений в довільну
точку
диничний
додатній заряд, поміщений в довільну
точку
M (x,y,z) діє сила
![]() (x,y,z) ,
(x,y,z) ,
що називається напруженістю електростатичного поля. Приклад 3. Поле швидкостей рухомої рідини. У гідромеханіці розподіл швидкостей рідини характеризується вектор-функцією
![]() (x,y,z)
(x,y,z)
/ для нестаціонарного руху
рідини
![]() (x,y,z,t) /.
(x,y,z,t) /.
Таким чином, вектор швидкостей
![]() відноситься не до конкретної частинки,
а до конкретної точки простору (x,y,z).
відноситься не до конкретної частинки,
а до конкретної точки простору (x,y,z).
Характеристикою скалярного поля є поверхні рівня. Аналогічно, векторне поле можна характеризувати так званими векторними лініями. Лінію, яка в кожній точці простору є дотичною до вектора, називають векторною лінією. В електростатиці векторні лінії називають силовими.
Знайдемо диференціальні рівняння, за якими можна визначити векторні лінії.
Як видно з рис.22, два вектори
![]() і
і![]() є колінеарними / з точністю до нескінченно
малих величин вищого порядку /, тому
є колінеарними / з точністю до нескінченно
малих величин вищого порядку /, тому
![]() =
0,
=
0,
або
-24-
Мінори, що відповідають ортам
![]() повинні дорівнювати нулеві отже
повинні дорівнювати нулеві отже
![]() ;
; ![]() ;
;![]() /6.6/
/6.6/
Це і є система рівнянь, за якими можна визначити сім’ю векторних ліній у просторі.
Зауважимо, що векторні лінії не повинні перетинатися, що надає умову однозначності на функцію.
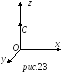 Задача
І. Знайти векторні лінії для випадку
векторного поля
Задача
І. Знайти векторні лінії для випадку
векторного поля![]() ,
,![]() .
.
Виберемо осі координат так, щоб вектор був напрямлений вздовж осі
![]()
![]() ,
, ![]()
![]()
Рівняння векторних ліній мають вигляд
![]()
Тобто
![]()
Звідси випливає, що
![]()
![]()
![]()
![]()
– концентричні кола, що
лежать в площинах, перпендикулярних до
вектора
![]() /центри кіл лежать на осі вектора
/центри кіл лежать на осі вектора![]() /.
/.
Задача 2. Показати, що для векторного поля на площині
![]()
![]()
Векторними лініями є сам’я прямих, що прохадять
-25-
через початок координат
![]()
П овернемось
до скалярного поля, заданого рівнянням
овернемось
до скалярного поля, заданого рівнянням![]() і розглянемо точку
і розглянемо точку![]() з координатами
з координатами![]() .
Значення функції
.
Значення функції![]() у сусідніх точках вже інші: в різних
напрямках
у сусідніх точках вже інші: в різних
напрямках![]() змінюється по різному.
змінюється по різному.
Введемо поняття похідної від скалярної функції за напрямком.
Напрямок, в якому нас цікавить
зміна функції
![]() ,
будемо характеризувати одиничним
вектором
,
будемо характеризувати одиничним
вектором![]() .
Розглянемо точку
.
Розглянемо точку![]() таку, що
таку, що![]() ,
де
,
де![]()
Тоді відношення
![]() /6.7/
/6.7/
будемо називати похідною в
точці
![]() від функції
від функції![]() у напрямку
у напрямку![]() .
.
Вважаючи
![]() малим, рокладемо
малим, рокладемо![]() в ряд Тейлора в околі точки
в ряд Тейлора в околі точки![]()
![]()
Підставляючи це вираз в /6.7/ одержимо
![]() /6.8/
/6.8/
Праву сторону /6.8/ можна інтерпретувати як скалярний добуток двох векторів

Вектор
![]() будемо називати градієнтом скалярної
функції
будемо називати градієнтом скалярної
функції![]() і введемо позначення
і введемо позначення
![]() /6.9/
/6.9/
-26-
Тоді /6.8/ можна записати
![]() )
)
Проектуючи /6.9/ на координатні осі матимемо
gradx 𝜑=![]() grady
𝜑=
grady
𝜑=![]() gradz
𝜑=
gradz
𝜑=![]()
або
gradxi 𝜑=![]()
і тому
![]()
Доведемо, що три часткові похідні
визначають вектор, тобто доведемо, що
![]() є вектором. Згадаємо, що при переході
однієї системи до іншої, вектори
перетворюються за законом.
є вектором. Згадаємо, що при переході
однієї системи до іншої, вектори
перетворюються за законом.
Ai=![]() i=1.2.3
i=1.2.3
а закон перетворення координат має вигляд
xi=![]() i=1.2.3
i=1.2.3![]() =
=![]()
При переході до нових координат
![]() =
=![]()
- похідні ![]() перетворюються за тим же законом, що й
компоненти вектора, отже
перетворюються за тим же законом, що й
компоненти вектора, отже![]() є вектором.
є вектором.
Часто замість символа ![]() вводять символ
вводять символ![]() / точніше символ
/ точніше символ![]() /,
тоді
/,
тоді
![]() 𝜑) /6.14/
𝜑) /6.14/
![]()
![]() /6.15/
/6.15/
![]() 𝜑=
𝜑=![]() /6.16/
/6.16/
Останню рівність можна записати символічно
![]() =
=![]()
розуміючи під ![]() диференціальний
оператор /оператор Гамільтона, оператор
набла/. Це лінійний оператор набла/. Це
лінійний оператор і тому справедливі
такі очевидні формули.
диференціальний
оператор /оператор Гамільтона, оператор
набла/. Це лінійний оператор набла/. Це
лінійний оператор і тому справедливі
такі очевидні формули.
-27-
![]()
![]() /6.18/
/6.18/
![]()
Задача 1. Знайти grad r, де r – віддаль від початку координат.
grad r=![]()
Тому, що
![]() маємо
маємо![]()
![]() =
=![]()
![]() grad r=
grad r=![]()
де ![]() - одиничний вектор напрямку радіус-вектора.
- одиничний вектор напрямку радіус-вектора.
Задача 2. Знайдемо ![]() де с – стала величина.
де с – стала величина.
gradx ![]() =c
=c![]() c*
c*![]()
grad ![]()
Задача 3.
![]()
Задача 4.
![]()
![]()
Повернемось тепер до формули для похідної від скалярної функції до напрямку
![]() )
)
Розкриваючи скалярний добуток можемо написати
![]() |
cos(
|
cos(![]() /6.19/
/6.19/
П роведемо
через точку М(x,y,z) відповідну поверхню
рівня і розглянемо випадок, коли вектор
роведемо
через точку М(x,y,z) відповідну поверхню
рівня і розглянемо випадок, коли вектор![]() дотичний до поверхні рівня. Оскільки,
на поверхні
дотичний до поверхні рівня. Оскільки,
на поверхні![]() ,
то.
,
то.![]()
Це можливо тільки тоді, коли cos(![]()
-28-
Таким чином, вектор ![]() перпендикулярний до поверхні рівня.
Якщо вектор
перпендикулярний до поверхні рівня.
Якщо вектор![]() орієнтований відносно поверхні рівня
довільно, то і вираз цей досягає
максимального значення, якщо
орієнтований відносно поверхні рівня
довільно, то і вираз цей досягає
максимального значення, якщо
cos(![]()
Тоді
![]()
якщо похідну від функції φ вираховують в напрямку, перпендикулярному до поверхні рівня.
Таким чином, градієнт скалярної функції – це вектор, перпендикулярний до поверхні рівня; його напрямок вказує напрямок найшвидшого зростання функції, а чисельно вектор-градієнт дорівнює похідній від функції за напрямком найшвидшого її зростання.
Приклад. Розглянемо топографічну карту, тобто поле висот
h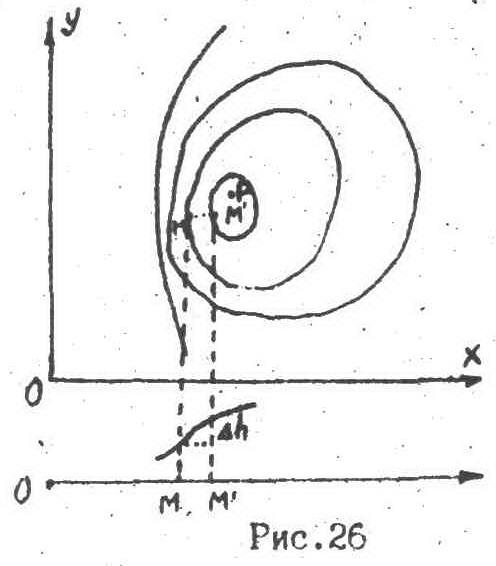 =h(x,y)
– кожній точці з координатами х,у
відповідає певне значення висоти h, а
точці Р – найбільша висота. Задача наша
двохмірна, тому йдеться про поверхні
рівня, а про лінії рівня – лінії однакової
висоти.
=h(x,y)
– кожній точці з координатами х,у
відповідає певне значення висоти h, а
точці Р – найбільша висота. Задача наша
двохмірна, тому йдеться про поверхні
рівня, а про лінії рівня – лінії однакової
висоти.
Вектор grad h у точці М показує напрям найбільш стрімкого підйому. Його числове значення вказує зміну висоти Δh при переході від точки М до точки М’ (ММ’=1). Обидві точки М і М’ лежать у площині ХУ.
Хто хоче доказати надто багато, не доказує нічого.
О. Бальзак
7.Похідна від вектора до напрямку.
Нехай задане векторне поле
![]()
- кожній точці простору відповідає свій
вектор ![]() .
Двом близьким точкам М і М’ відповідають
різні за величиною і напрямком вектори
.
Двом близьким точкам М і М’ відповідають
різні за величиною і напрямком вектори![]() і
і![]() Напрямок охарактеризуємо одиничним
вектором
Напрямок охарактеризуємо одиничним
вектором![]() ,
,
- 29
29
так, що ![]() ε
ε![]()
Як і в випадку скалярного поля, введемо
поняття похідної від вектора ![]() за
напрямком
за
напрямком![]() .
.
![]() =
=![]() /7.1/
/7.1/
Тоді ![]()
Підставляючи цей вираз в /7.1/ одержимо
![]() /7.2/
/7.2/
Вираз в дужках є скалярним добутком
вектора ![]() і вектора набла.
і вектора набла.
Отже,![]() /7.3/
/7.3/
або ,![]() /7.4/
/7.4/
Напрямок ММ’ не обов’язково треба
характеризувати вектором ![]() Вводячи вектор
Вводячи вектор![]() ,
напрямок якого збігається з напрямком
ММ’, можна говорити про похідну від
вектора
,
напрямок якого збігається з напрямком
ММ’, можна говорити про похідну від
вектора![]() по вектору
по вектору![]() Узагальнюючи
/7.2/ одержуємо
Узагальнюючи
/7.2/ одержуємо
,![]() /7.5/
/7.5/
Тобто
![]() /7.6/
/7.6/
Розглянемо випадок нестаціонарного поля
![]()
і знайдемо повну похідну по часі від функції φ. Маємо
![]()
Тобто ![]() /7.7/
/7.7/
Аналогічно для векторного поля
![]()
-30-
Або
![]()
Приклад. Застосуємо /7.8/ до векторного
поля швидкості рідини ![]()
Тоді ![]()
Як видно, повне прискорення ![]() складається з двох доданків: локального
прискорення
складається з двох доданків: локального
прискорення![]() і переносного /трансляційного/ прискорення
.(
і переносного /трансляційного/ прискорення
.(![]()
Хіба відмовлюсь я від свого обіду тільки тому, що я не до кінця розумію процес травлення.
О.Хевісайд
8. Потенційне векторне поле. Лінійний інтеграл від вектора
Кожній точці скалярного поля ![]() завжда можна поставити в відповідність
вектор-градієнт функції.
завжда можна поставити в відповідність
вектор-градієнт функції.
![]()
Нехай задане довільне векторне поле
![]() .
Чи можна знайти функцію φ(x,y,z) таку, щоб
.
Чи можна знайти функцію φ(x,y,z) таку, щоб
![]()
Виявляється, що така функція існує не завжди і тому дамо таке означення.
Якщо існує функція φ така, що ![]() ,
то вектор
,
то вектор![]() називають потенційним вектором. Поле
такого вектора називають потенціальним
полем, а функцію φ називають потенціалом
векторного поля.
називають потенційним вектором. Поле
такого вектора називають потенціальним
полем, а функцію φ називають потенціалом
векторного поля.
Щоб з’ясувати, за яких умов вектор ![]() є потенціальним, необхідно ввести
поняття лінійного інтеграла від вектора.
є потенціальним, необхідно ввести
поняття лінійного інтеграла від вектора.
 Z
Z![]()
![]()
![]()
M ![]()
A
O X
Y
У координатній системі x,y,z розглянемо
векторне поле ![]() і виберемо довільну криву С. Розіб’ємо
криву на малі ділянки
і виберемо довільну криву С. Розіб’ємо
криву на малі ділянки![]() ;
кожній ділянці поставимо у відповідність
вектор
;
кожній ділянці поставимо у відповідність
вектор![]() ,
який відповідає одній з точок на ділянці
,
який відповідає одній з точок на ділянці![]() кривої. Розглянемо тепер суму
кривої. Розглянемо тепер суму![]() Вираз цей неоднозначний: він істотно
залежить
Вираз цей неоднозначний: він істотно
залежить
-31-
від того, на скільки ділянок ми розбили
криву С. При цьому дугу ваваі замінюємо
відрузком ![]() .
Не зовсім зрозуміло, в якій точці
/наприклад М чи М’/ розглянемо
вектор
.
Не зовсім зрозуміло, в якій точці
/наприклад М чи М’/ розглянемо
вектор![]() Щоб уникнути неоднозначності, криву С
доцільно розробити на нескінченно
багато нескінченно малих ділянок
Щоб уникнути неоднозначності, криву С
доцільно розробити на нескінченно
багато нескінченно малих ділянок![]() Тоді границю
Тоді границю
![]() =
=![]() /8.1/
/8.1/
називають лінійним інтегралом від
вектора ![]() вздовж кривої С. у загальному випадку
значення цього інтеграла залежить не
тільки від вигляду векторної функції
вздовж кривої С. у загальному випадку
значення цього інтеграла залежить не
тільки від вигляду векторної функції![]() але і від форми кривої С.
але і від форми кривої С.
Якщо крива С замкнена, то лінійний
інтеграл від вектора
![]() називають циркуляцією вектора
називають циркуляцією вектора![]() вздовж кривої С і позначають
вздовж кривої С і позначають
![]() =
=![]() /8.2/
/8.2/
Лінійний інтеграл від вектора
– криволінійний інтеграл – узагальнює
поняття звичайного інтеграла. З![]() вичайний
інтеграл є частинним випадком /8.1/, коли
крива С переходить у відрізок прямої
осі Х.
вичайний
інтеграл є частинним випадком /8.1/, коли
крива С переходить у відрізок прямої
осі Х.
Загальних правил обчислення криволінійних інтегралів немає. Обчислення такого інтеграла намагаються звести до обчислення звичайного інтеграла. Це можливо тоді, коли підінтегральний вираз вдається звести до повного диференціала.
Задача 1. Обчислити інтеграл. ![]()

якщо С – коло радіуса а.
Перейдемо до полярних координат.
x=a cos𝜑 dx= -asin𝜑d𝜑
y=a sin𝜑 dy= a cos𝜑d𝜑
Тоді
. ![]()
Задача 2. Знайти циркуляцію вектора ![]() .
.
![]() вздовж замкненої кривої С, обмеженої
координатними осями і першою четвертиною
астероїди.
вздовж замкненої кривої С, обмеженої
координатними осями і першою четвертиною
астероїди.
![]() +a
+a![]()
Вираз
![]()
-32-
с кладається
з трьох доданків
кладається
з трьох доданків
![]()
На астероїді
x=a![]() dx=-3a
dx=-3a![]()
y=a![]() dy=3a
dy=3a![]()
![]()
![]()
На ділянці ОМ:
Y=0 ![]() d
d![]()
![]()
![]()
Легко побачити, що
![]() і, остаточно
і, остаточно![]()
Теорема. Лінійний інтеграл від потенційного вектора вздовж кривої, яка починається в точці М0 і закінчується М1, не залежить від вигляду кривої і дорівнює різниці значень функції φ у точках М1 і М0. Зокрема, циркуляція потенційного вектора здовж довільного контура дорівнює нулеві.
C 1
M1(x1.y1.z1)
1
M1(x1.y1.z1)
C
M0(x0.y 0.z0) Для доказу зауважимо, що для потенціального вектора.
![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
і тоді ![]() =
=![]()
Підінтегральний вираз є повним диференціалом функції φ і тому
![]() /8.3/
/8.3/
Якщо крива замкнена, то точки М1 і М0 збігаються і
![]() /8.4/
/8.4/
Таким чином, ![]() /8.3’/
/8.3’/
![]() =0 /8.4’/
=0 /8.4’/
-33-
Можна довести і обернену теорему.
Якщо циркуляція вектора ![]() по довільному контуру дорівнює нулеві,
то вектор
по довільному контуру дорівнює нулеві,
то вектор![]() – потенціальний /векторне поле-потенціальне/,
тобто існує така функція φ, що
– потенціальний /векторне поле-потенціальне/,
тобто існує така функція φ, що
![]()
Формули /8.3/ і /8.4/ не є зручним для
перевірки, чи якесь векторне поле ![]() є потенціальним. Знайдемо більш ефективні
формули.
є потенціальним. Знайдемо більш ефективні
формули.
Якщо поле![]() потенціальне, то
потенціальне, то
![]()
![]()
![]()
Продиференціюємо першу з цих рівностей, то у, другу – по х, тоді
![]()
![]()
Звідси випливає, що
![]()
Аналогічно одержуємо ще дві рівності. Отже,
![]()
![]()
![]() /8.5/- умови потенціальності векторного
поля.
/8.5/- умови потенціальності векторного
поля.
Приклад. Електростатичне поле. Напруженість поля, створеного системою зарядів е1, е2…еп можна записати
![]() 𝜑=
𝜑=![]()
- електростатичне поле потенціальне. Інтеграл.
![]()
має прямий фізичний зміст – він виражає роботу, яку виконує поле при переміщенні одиничного додатного заряду вздовж кривої С. Умова
![]() =0
=0
виражає те, що робота переміщення заряду вздовж замкненої кривої дорівнює нулеві.
Приклад 2. Широким класом рухів рідини
є її потенціальний рух. Для такого руху
можна ввести функцію φ(x,y,z), що ![]()
Функцію φ називають потенціалом швидкостей.
Задача 1. Перевірити, чи є потенціальним векторне поле
![]()
Маємо
![]()
![]() =2yz
=2yz
- поле не потенціальне, не існує така
функція φ, щоб ![]() .
.
-36-
Вирази ![]() можна записати через диференціали
координат.
можна записати через диференціали
координат.
Р озглянемо
площадку
озглянемо
площадку![]() і спроектуємо її на площину ху. З точністю
до малих величин вищого порядку
і спроектуємо її на площину ху. З точністю
до малих величин вищого порядку
![]()
і тому![]()
Аналогічно
![]()
![]()
Таким чином
![]() /9.5/
/9.5/
Якщо ![]() то
то![]()
а коли поверхня S замкнена ![]()
Ця рівність очевидна для поверхні куба. Дійсно /рис.38/
![]()
Об’єм, обмежений довільною поверхнею S можна розбити на нескінченно велике число елементарних кубиків. Розглянемо два сусідні кубики 1 і 2 /для неточності на рис. 39 вони зображені окремо зі спільною гранню ABCD/. Тоді
d![]()
Інтеграл
![]()
Можна розглядати як суму подібних інтегралів по поверхні всіх кубиків. Тому, що
![]()
Для кожного з кубиків, то і
![]() /9.6/
/9.6/
-37-
або в проекціях на координатні осі
![]()
![]()
![]() .
.
для довільної поверхні
Обчислення поверхневих інтегралів
пов’язане з серйозними труднощами. У
випадку, кола S є площиною, інтеграл ![]() зводиться до звичайного двохкратного
інтеграла. Якщо поверхня S, по якій
ведеться інтегрування, є замкненою, то
часто вирахування поверхневого інтеграла
зводиться інтегрування, є замкненою,
то часто вирахування поверхневого
інтеграла зводять до вирахування
об’ємного /трьохкратного/ інтеграла.
Для цього користуються теоремою
Остроградського-Гаусса, про яку йтиме
мова пізніше.
зводиться до звичайного двохкратного
інтеграла. Якщо поверхня S, по якій
ведеться інтегрування, є замкненою, то
часто вирахування поверхневого інтеграла
зводиться інтегрування, є замкненою,
то часто вирахування поверхневого
інтеграла зводять до вирахування
об’ємного /трьохкратного/ інтеграла.
Для цього користуються теоремою
Остроградського-Гаусса, про яку йтиме
мова пізніше.
Задача 1. Підрахувати потік радіус-вектора
![]() через зовнішню поверхню прямого кругового
циліндра /Н – висота, R – радіус основи/.
через зовнішню поверхню прямого кругового
циліндра /Н – висота, R – радіус основи/.
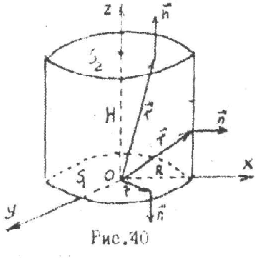 Поверхня
S складається з трьох частин: з бічної
поверхні циліндра і двох основ:
Поверхня
S складається з трьох частин: з бічної
поверхні циліндра і двох основ:
![]() Тому
Тому![]() Тут
Тут![]() (
(![]() )
)
Для бічної поверхні ![]()
![]() Для
S2:
Для
S2:![]()
![]() y
y
Остаточно маємо ![]()
Задача 2. Знайти потік радіус-вектора
![]() через зовнішню поверхню прямого конуса
/Н – висота, R – радіус основи/. Вказівка:
врахувати, що для бічної поверхні
через зовнішню поверхню прямого конуса
/Н – висота, R – радіус основи/. Вказівка:
врахувати, що для бічної поверхні![]()
В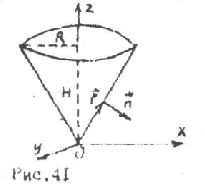 ідповідь:
ідповідь:![]()
-38-
Повернемось до поля швидкостей рухомої рідини
![]()
 і розглянемо довільну замкнену поверхню
S, що обмежує об’єм V. Для правої частини
поверхні /рис.43/ кут між векторами
і розглянемо довільну замкнену поверхню
S, що обмежує об’єм V. Для правої частини
поверхні /рис.43/ кут між векторами![]() і
і![]() є гострим
є гострим![]() ,
і
,
і![]()
Для лівої частини поверхні ![]()
Кожний з цих інтегралів має прямий фізичний зміст: перший визначає кількість рідини, яка за одну секунду виходить з об’єму V, другий – кількість рідини, яка за одну секунду входить в об’єм V. Оскільки
![]()
![]() визначає різницю між кількістю рідини,
яка за одну секунду виходить з об’єму
V і кількістю рідини, яка за одну секунду
входить в об’єм V.
визначає різницю між кількістю рідини,
яка за одну секунду виходить з об’єму
V і кількістю рідини, яка за одну секунду
входить в об’єм V.
Як відомо, реальні рідини можна вважати нестисливими. Це означає, що кількість рідини, яка входить за одну секунду в об’єм V мусить дорівнювати кількості рідини, яка за одну секунду виходить з об’єму V. Отже,
![]() /9.7/
/9.7/
математична умова нестисливості рідини. Для інших середовищ, наприклад для газів,
![]()
Далі будемо розглядати нестисливу рідину, однак припустимо, що
![]()
Це можливе тоді, коли в об’ємі V існують «джерела», які можуть народжувати або знищувати рідину /в дійсності цього не буває, тому що діє закон збереження речовини/. Ми можемо говорити про додатні джерела, якщо
![]()
-39-
/рідина невластива, однак об’єму V за одну секунду виходить більше рідини, ніж входить/, або про від’ємні джерела, коли
![]()
Н ам
необхідно ввести кількісну величину,
яка б характеризувала інтенсивність
джерела в точці М з координатами x,y,z.
ам
необхідно ввести кількісну величину,
яка б характеризувала інтенсивність
джерела в точці М з координатами x,y,z.
Оточимо точку М поверхнею S, що обмежує об’єм V. Тоді
![]() Будемо називати дивергенцію /розбіжністю/
вектора швидкості
Будемо називати дивергенцію /розбіжністю/
вектора швидкості
![]()
Розглянемо довільне векторне поле
![]()
Трактуючи його як поле швидкостей
певної фіктивної рідини, можна говорити
про джерела цього поля. Аналогічно до
/9.8/, дивергенцію векторного поля ![]() визначають як розрахований на одиницю
об’єму потік вектора А через поверхню
нескінченого малого об’єму, яка оточує
точку М:
визначають як розрахований на одиницю
об’єму потік вектора А через поверхню
нескінченого малого об’єму, яка оточує
точку М:

![]() /9.9/
/9.9/
Щоб знайти аналітичний вираз для дивергенції вектора в точці М приймемо цю точку за початок координат, об’єм V виберемо у вигляді паралелепіпеда з нескінченно малими ребрами x,y,z.
Обчислимо вираз
![]()
Компоненту Ах(x,y,z) розкладемо в ряд Тейлора в околі початку координат.
![]()
де ε – нескінченно мала величина вищого
порядку. Перший додаток виразу ![]() матиме вигляд
матиме вигляд
-40-

Обчислимо окремі інтеграли
. Насамперед звернемо увагу на те , що
нормаль до замкненої поверхні завжди
напрямлена назовні, тому площадку
М’А’В’С’ треба трактувати як ![]() ,
,
А площадку МАВС – як -
площадку МАВС – як -![]() .Координати точок Р і Q , в яких прикладені
вектори нормалі n ,такі:
.Координати точок Р і Q , в яких прикладені
вектори нормалі n ,такі:
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
Тоді
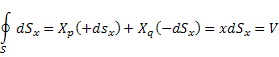
![]()
![]()
Якщо врахувати ще , що ![]() то
то

Таким чином ,
![]() =0
=0
Підставляючи цей вираз у /9,9 / одержимо
![]()
Початок координат можна вибрати довільно , тому одержана формула справедлива для будь-якої точки простору і тому
![]() /9.10/
/9.10/
Або в скороченому записі
![]() /9.11/
/9.11/
Використовуючи оператор набла
![]()
І враховуючи , що ![]()
-41-
Вираз для дивергенції
вектора можна записати як скалярний
добуток векторів ![]()
![]() /9,12/
/9,12/
Теорема . Дивергенція вектора є інваріантом відносно повороту координатної системи.
Доведення . Від системи координат х ,у , z перейдемо до системи x’ ,y’ , z’ тоді
![]()
![]()
![]()
Далі маємо очевидний ланцюг рівностей
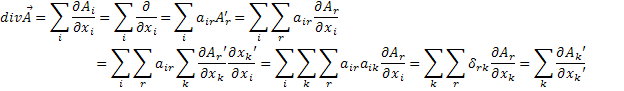
Більш просте доведення цієї
теореми випливає з того , що дивергенція
вектора є скалярним добутком векторів
![]() , а скалярний добуток двох векторів є
інваріантом .
, а скалярний добуток двох векторів є
інваріантом .
Відзначимо цікавий , на
перший погляд парадоксальний факт .
Вектор нормалі до замкнутої поверхні
і орієнтований назовні до поверхні ,
як відзначалось , завжди перпендикулярний
до поверхні і орієнтований нозовні до
поверхні . Його треба трактувати як
полярний вектор . у випадку відкритої
площадки ![]() вектор нормалі є аксіальним , тому що
доводиться говорити про напрямок обходу
контура площадки.
вектор нормалі є аксіальним , тому що
доводиться говорити про напрямок обходу
контура площадки.
Задача 1.Обчислити ![]() , де
, де ![]() - радіус – вектор точки .
- радіус – вектор точки .
Розвязок
![]()
Задача 2. Обчислити ![]() , де
, де ![]() – сталий вектор
– сталий вектор
Розвязок
![]()
-42-
Задача 3.
Обчислити ![]() , де
, де ![]() -
скалярна , А – векторна функцію .
-
скалярна , А – векторна функцію .
Розвязок
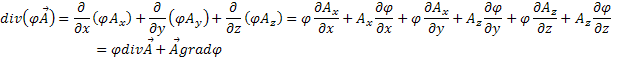
Задача 4. Довести рівності
![]()
![]()
![]()
![]()
![]() -сталі
-сталі
Задача 5. Довести , що дивергенція псевдовектора є псевдоскаляром .
Математика стала інтелектуальним
Знаряддям фізика :
Тільки вона дає змогу науково
Точно виражати пізнані закони
Природи і застосувати їх до
Складних процесів
М. Лауе
10.Теорема Остроградського-Гауса
Теорема. Потік вектора через довільну замкнену поверхню дорівнює інтегралові від дивергенції цього вектора по обєму , обмеженому цією поверхнею.
![]() /10.1/
/10.1/
Доведення: Розібємо обєм Vна
велику кількість малих обємів ![]() виберемо в формі кубиків , сума обємів
яких становить V .
виберемо в формі кубиків , сума обємів
яких становить V .
Для кожного елементарного обєму справедлива рівнвсть
![]() /10.2/
/10.2/
-43-
 Де
Де
![]() -поверхня
кубика ,
-поверхня
кубика , ![]() -
мала величина /
-
мала величина / ![]()
![]() 0 , коли
0 , коли ![]() /.
/.
Помножимо /10.2/ на
, ![]() тоді
тоді
![]()
![]()
Де ![]() .Такі нерівності можна написати для
всіх кубиків . Додаючи їх отримаємо
.Такі нерівності можна написати для
всіх кубиків . Додаючи їх отримаємо
Де ![]() .Такі нерівності можна написати для
всіх кубиків . Додаючи їх отримаємо
.Такі нерівності можна написати для
всіх кубиків . Додаючи їх отримаємо

Бо інтеграли по всіх внутрішніх гранях знищуються . Отже
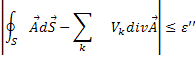
Нехай тепер всі ![]() , тоді і
, тоді і ![]() , а сума переходить в інтеграл і остаточно
одержуємо
, а сума переходить в інтеграл і остаточно
одержуємо
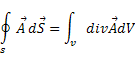
Теорема Остроградського – Гауса широко застосовується в математиці і в фізиці . Зокрема , вона дає змогу звести вираховування поверхневих інтегралів до вираховування обємних інтегралів .
Приклад. Електричні заряди
створюють електростатичне поле . розподіл
зарядів у просторі характеризується
їх обємною густиною![]() - кількість зарядів в одиниці об’єму .
Напруженість електростатичного поля
- кількість зарядів в одиниці об’єму .
Напруженість електростатичного поля
![]() в порожнечі визначається за допомогою
першого рівняння Максвела
в порожнечі визначається за допомогою
першого рівняння Максвела
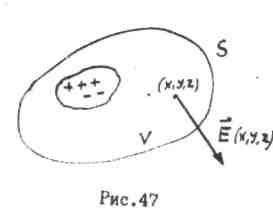
![]()
Про інтегруємо цю рівність по довільному об’єму
![]()
і застосуємо теорему Остроградського - Гаусса . Тоді
![]()
Потік вектора напруженості електричного поля
через довільну замкнену поверхню S дорівнює алгебраїчній
сумі зарядів об’ємі , обмеженому цією поверхнею .
-44-
Задача. Обчислити потік радіус
– вектора ![]() через замкнену поверхню S , що обмежує
об’єм V.
через замкнену поверхню S , що обмежує
об’єм V.
Використовуючи теорему Остроградського – Гаусса маємо

![]()
а тому що![]() /порівняйте
9 , задачі 1 , 2 /.
/порівняйте
9 , задачі 1 , 2 /.
Задача. Обчислити потік
радіус – вектора ![]() через замкнену поверхню S , що обмежує
об’єм V.
через замкнену поверхню S , що обмежує
об’єм V.
Використовуючи теорему Остроградського – Гаусса маємо
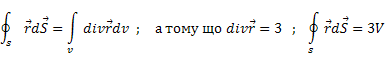
/порівняйте 9 , задачі 1 , 2 /.
Роаумна істота, яка в кокний данний
Момент знала б всі рушійні сили природи
і мала б повну картину стану, в якому
природа знаходиться, могла б - якщо би
тільки її розум був в стані достатньо
проаналізувати ці дані - виразити одним
рівнннням як рух найбільших сил світу,
так і рух найдрібніших атомів. Нічого не
залишилось би для неї невідомим, і вона
могла б оглянути одним поглядом як
майбутне , так і минуле.
П.Лаплас: Аналогична теорія ймовірностей
11. Рівняння Лапласа
Розглянемо
скалярну функцію ![]() , яка визначає скалярне поле . У
відповідність цьому полеві можна
поставити векторне поле його градієнта
, яка визначає скалярне поле . У
відповідність цьому полеві можна
поставити векторне поле його градієнта
![]() /11.1/
/11.1/
Знайдемо ![]() . Маємо
. Маємо
![]()
Оператор
![]() /11.2/
/11.2/
-45-
Називають оператором Лапласа
, Таким чином ![]() /11.3/
/11.3/
Легко переконатись , що ![]() /11.4/
/11.4/
Дійсно ![]()
Розглянемо тепер функцію
![]() /11/5/
/11/5/
Де с – стала величина , ![]() - віддаль від початку координат .
- віддаль від початку координат .
Знайдемо ![]()
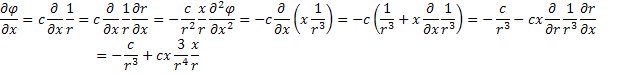
Таким чином ,
![]()
![]()
![]()
![]()
![]()
Рівняння /11.6/ називають рівнянням Лапласа. Це диференціальнв рівняння другого порядку з частинними похідними , лінійне , однорідне . Як і всяке рівняння з частинними похідними , воно допускає безліч розв’язків . Загальний розв"язок такого рівняння визначаеться з точністю до довільних функцій . Наприклад , розвязком рівняння /11.6/ є
![]()
але розв"язком буде також
![]()
Однозначний розв’язок рівняння Лапласа можна знайти тільки тоді, коли задані граничні умови – вигляд функції /або її похідних/ на границі області .
-46-
Прикладом функції /11.5/ є електростатичний потенціал
![]()
поля, створеного
точковнм зарядом С
. У
випадках, коли поле створена більш
складною системою зарядів /заряди
роэподілеиі в об"емі або на поверхні
/, очевидно, електростатичний потенціал
визначений складнішою функцією. Ми
знайдемо її
/для
областей простору, де відсутні заряди/,
роав язуючи рівняння Лапласа ![]() .
.
Багато я навчився у
моїх наставників, та ще більше
у моїх товарищі в і найбільше у моїх учнів.
Талмуд
12. Ротор вектора
Розглянемо векторне поле
![]() /12.1/
/12.1/
У загальному випадку лінійний інтеграл від цього вектора
![]() /12.2/
/12.2/
Залежить від вигляду контура
інтегрування С . Тільки в тому випадку
, коли векторне поле потенціальне ,
тобто , коли існує така функція ![]() , що
, що ![]() , лінійний інтеграл не залежить від
шляху інтегрування і також
, лінійний інтеграл не залежить від
шляху інтегрування і також
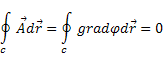
Розглянемо випадок , коли векторне поле потенціальне . Тоді , очевидно
![]() /12.3/
/12.3/
Перед тим , як ввводити поняття про ротор векторного поля , треба провести деякі попередні обчислення.
Розглянемо площадку S , обмежену контуром
Вважаючи S векторною величиною , маємо
![]() /12.4/
/12.4/
![]() /12.5/
/12.5/
При цьому
-47-
![]() ;
; ![]() ;
; ![]() ; /12.6/
; /12.6/
 Далі
мають місце очевидні формули
Далі
мають місце очевидні формули ![]()
![]() /12.8/
/12.8/
Знайдемо інтеграл
/![]()
Інтегруваши по контуру С
можна замінити
інтегруванням по
контуру ![]() . Це
тому , що змінні x , y однакові як для
точки Р , так і для точки Q
, /рис.49/, для цих точок
різні тільки аплікати Z. З рис.5О видно
, що
. Це
тому , що змінні x , y однакові як для
точки Р , так і для точки Q
, /рис.49/, для цих точок
різні тільки аплікати Z. З рис.5О видно
, що
![]() /12.9/
/12.9/
Дійсно , інтегрування по
кривій AMB дає
площу фігури EAMFB з
протилежним знаком /напрямок інтегрування
визначений стрілкою від В до А /,
інтегрування по кривій ANB дає площу
фігури EANFB. Результатом інтегрування
є величина плащі , обнаженої контуром
![]() з відємним знаком.
з відємним знаком.
Аналог!чно доводиться, що
![]()
![]()
![]()
![]()
![]() /12.10/
/12.10/
Введемо тепер поняття ротора вектора.
А(*,ИУ
Р озглянемо
векторне полеA(X,Y,Z).
В
околі початку координат розглянемо
площадку S , обмежену
контуром С. Вираз
озглянемо
векторне полеA(X,Y,Z).
В
околі початку координат розглянемо
площадку S , обмежену
контуром С. Вираз
![]() /12.11/
/12.11/
Рис.51 Показує наскільки векторне поле А відхиляється від потенціального в початку координат 0 . Питания ускладнюеться тим, що площадку можна оріентувати в просторі по різному . При різних орієнтаціях площадки /а значить і контура С / підрахунок виразу
-48-
/12.12/ даватиме , взагалі кажучи , різні результати . Тому приймемо , що
Де ![]() - вектор , який характеризує відхилення
векторного поля від потенціальності .
Вектор
- вектор , який характеризує відхилення
векторного поля від потенціальності .
Вектор![]() називають ротором вектора
називають ротором вектора![]() . Щоб знайти вираз для ротора вектора
, розглянемо інтеграл
. Щоб знайти вираз для ротора вектора
, розглянемо інтеграл

І розкладемо ![]() у ряд Тейлора по степенях x ,y ,z в околі
початку координат . Обмежуючись членами
першого порядка мализни , одержуємо
у ряд Тейлора по степенях x ,y ,z в околі
початку координат . Обмежуючись членами
першого порядка мализни , одержуємо
![]()
Тоді
![]()
Використовуючи /12.7/-/12.10/ одержимо
![]()
Аналогічно ![]()
![]()
Підставивши ці вирази в /12.12/ і врахувавши
, що всі ![]() , ми одержимо
, ми одержимо
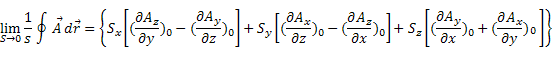
А з урахуванням /12.6/
![]()
Ця рівність справедлива в початку координат , але його можна вибрати в будь-якій точці простору . Отже , остання рівність справедлива в будь-якій точці простору і тому
![]()
З другого боку
![]()
Порівнюючи дві останні рівності , одержуємо
-49-
![]()
![]() /12.14/
/12.14/
![]()
Таким чином , векторному полеві ![]() відповідає новий вектор
відповідає новий вектор![]() , компоненти якого визначені формулами
/12.14/ . Отже ,
, компоненти якого визначені формулами
/12.14/ . Отже ,
![]() /12.15/
/12.15/
Або
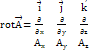 /12.16/
/12.16/
Згадуючи формулу /3.13/ , ми можемо
записати ротор вектора ![]() як векторний добуток вектора набла на
вектор
як векторний добуток вектора набла на
вектор
![]() /12.17/
/12.17/
Тут доречно згадати , що дивергенція
вектора ![]() -
це скалярний добуток векторів
-
це скалярний добуток векторів![]()
![]()
Задача 1 . Обчислити ![]()
![]()
Тому ![]()
Задача 2 . Довести рівності
![]()
![]()
![]()
![]()
![]()
-50-
Розкажи мені твоє минуле ,
А я скажу , яке буде твоє майбутнє .
Конфуцій
13 . Теорема Стокса
Теорема . Циркуляція вектора по замкненому контуру дорівнює потокові ротора цього вектора через довільну поверхню , яка спирається на цей контур
![]() /13.1/
/13.1/
Д оведення
. Розглянемо контур С і довільну поверхню
S , що спирається на цей контур . Нагадаємо
визначення ротора вектора
оведення
. Розглянемо контур С і довільну поверхню
S , що спирається на цей контур . Нагадаємо
визначення ротора вектора
![]()
Розібємо поверхню S на
невелику кількість площадок ![]() , тоді
, тоді
![]() ,
,
Де ![]() , якщо
, якщо![]() . Додамо нерівності /13.3/ для всіх площадок
. Додамо нерівності /13.3/ для всіх площадок
![]() і врахуємо що
і врахуємо що

![]()
Дійсно , інтегрування по
всіх внутрішніх елементах контурів
![]() скорочується і залишається тільки
інтеграл по елементах зовнішнього
контура С . Нехай тепер всі
скорочується і залишається тільки
інтеграл по елементах зовнішнього
контура С . Нехай тепер всі![]() тоді
тоді![]() а сума
а сума
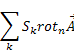
Переходить у поверхневий інтеграл
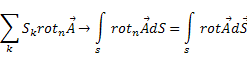
Остаточно отримаємо /13.1/
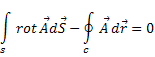
-51-
Наголосимо ще раз , що ротор ![]() показує наскільки векторне поле
показує наскільки векторне поле![]() відхиляється від потенціального . Як
бачимо , ротор потенціального поля
дорівнює нулеві
відхиляється від потенціального . Як
бачимо , ротор потенціального поля
дорівнює нулеві
![]() /13.4/
/13.4/
Це рівняння безпосередньо випливає з
теореми Стокса . Дійсно ,

Отже , за теоремою Стокса ![]()
А тому , що поверхня S – довільна
![]()
Приклад . Закон електромагнітної індукції . Нехай контур С знаходиться у магнітному полі з індукцією β . потік індукції через поверхню дорівнює

![]()
Зміна в часі цього потоку призводить до виникнення електрорушійної сили індукції в контурі С , яку визначають як циркуляцію напруженості електростатичного поля
![]()
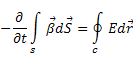
Застосуємо теорему Стокса
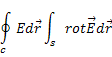
І завважимо , що
![]()
Порівнюючи підінтегральні вирази , одержимо рівняння Максвела , яке описує явище електромагнітної індукції
![]()
Дуже радимо всім розв’язувати задачі . Ні для кого не є секретом , що математику вчать розв’язуючи задачі а не спостерігаючи , як їх розв’язують інші .
М. Рід , В . Саймон
14. Деякі формули векторного аналізу
Виведемо декілька тотожностей з векторного аналізу , які часто
-52-
Використовуються в тензорній фізиці.
Знайдемо rot (φĀ), де φ – скалярна функція. Проекція цього виразу на вісь х дорівнює
 rotх
(φ
rotх
(φ )
=
)
=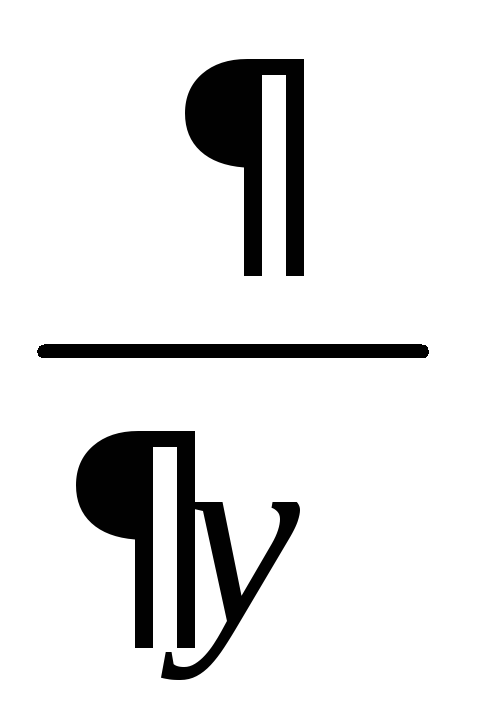 (φAz)
–
(φAz)
–
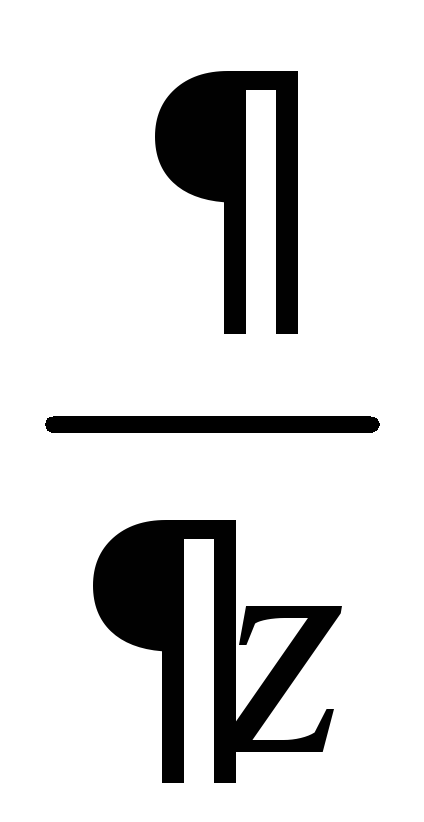 (φAy)
=
(φAy)
=
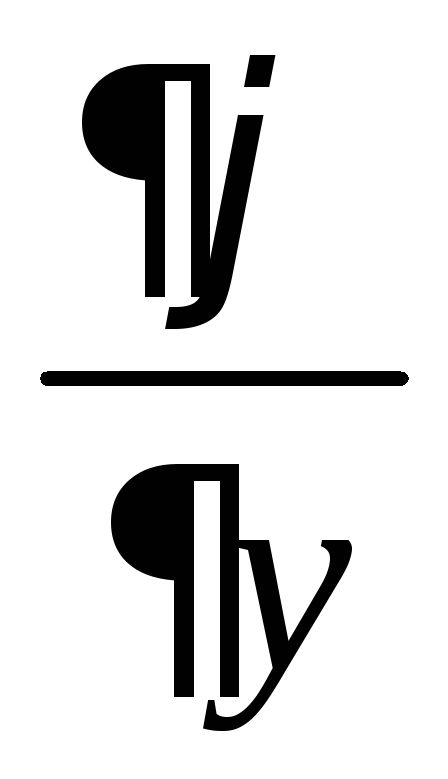 Az
+
φ
Az
+
φ –
–
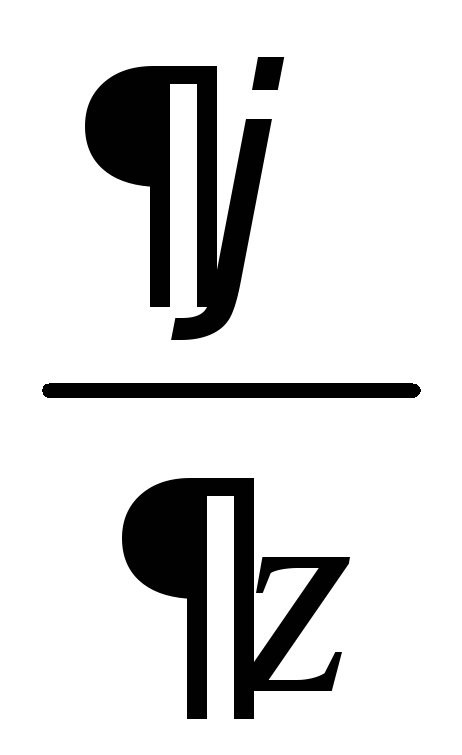 Ay
–
φ
Ay
–
φ =
=
= φ![]() –
–![]() +
grad y
φAz
–
grad z
Ay
= φ rot х
+
grad y
φAz
–
grad z
Ay
= φ rot х
![]() -
-![]() х
х
Подібні вирази одержимо для rot y (φĀ) і для rot z (φĀ), тому
rot (φ![]() )
= φ rot
)
= φ rot![]() -
-![]() /14.1/
/14.1/
Переконаймось, що дивергенція ротора векторного поля дорівнює нулеві
div rot
![]() =
=![]() rotх
rotх
![]() +
+![]() rotу
rotу![]() +
+![]() rot z
rot z
![]() =
=![]() (
(![]() -
-![]() )
+
)
+![]() (
(![]() -
-![]() )+
)+![]() (
(![]() -
-
![]() )
)
div rot
![]() = 0 /14.2/
= 0 /14.2/
поле ротора не має джерел.
3.Щоб знайти градієнт квадрата
вектора
![]() ,розглянемо
його х - компоненту
,розглянемо
його х - компоненту
grad
х
![]() =
=![]() (
(![]() +
+![]() +
+![]() )
= 2 Aх
)
= 2 Aх
![]() + 2 Ay
+ 2 Ay![]() + 2 Az
+ 2 Az![]() = 2 Aх
= 2 Aх![]() + 2 Ay
+ 2 Ay![]() +
+
+ 2 Az![]() +
2 Ay
+
2 Ay
![]() +
2 Az
+
2 Az![]() - Aх
- Aх
![]() -
2 Az
-
2 Az![]() = 2(Aх
= 2(Aх![]() +
Ay
+
Ay![]() + Az
+ Az![]() )
Aх +
)
Aх +
+ 2 Aу
(![]() -
-![]() )
+ 2 Az
(
)
+ 2 Az
(![]() -
-![]() )
= 2(
)
= 2(![]()
![]() )
Aх +
2 Ay
rot z
)
Aх +
2 Ay
rot z
![]() -
2 Az
rot у
-
2 Az
rot у![]() =
=
= 2(![]()
![]() )
Aх +
2
)
Aх +
2
![]()
![]() Звідси
робимо висновок, що
Звідси
робимо висновок, що
grad
![]() =
2(
=
2(![]() grad)
grad)![]() +
+![]() / 14.3/
/ 14.3/
4.Дивергенція векторного добутку двох векторів дорівнює
div![]() =
=![]()
![]() х
+
х
+![]()
![]() у
+
у
+![]()
![]() z
=
z
=
![]() (AуВz
- AzВy)
+
(AуВz
- AzВy)
+
![]() (AzВx
- AxВz)
+
(AzВx
- AxВz)
+
+![]() (AxВy
- AyВx)
=
(AxВy
- AyВx)
=
![]() Вz
+ Ay
Вz
+ Ay![]() -
-![]() Вy –
Az
Вy –
Az
![]() +
+![]() Вx
+ Az
Вx
+ Az
![]() -
-
![]() Вz
– Ax
Вz
– Ax![]() +
+![]() Вy
+ Ax
Вy
+ Ax![]() -
-![]() Вx -
Ay
Вx -
Ay![]() =
=
-53-
= Вx
(![]() -
-
![]() )
+ Вy
(
)
+ Вy
(![]() -
-
![]() )
+ Вz
(
)
+ Вz
(![]() -
-
![]() )
– Ax(
)
– Ax(![]() -
-![]() )
–
Ay
(
)
–
Ay
(![]() -
-![]() )
–
)
–
- Az
(![]() -
-![]() )
= Вx
rot х
)
= Вx
rot х
![]() + Вy
rot y
+ Вy
rot y
![]() + Вz
rot z
+ Вz
rot z
![]() - Ax
rot x
- Ax
rot x
![]() - Ay
rot y
- Ay
rot y
![]() - Az
rot z
- Az
rot z
![]()
Oтже, div![]() =
=![]() rot
rot![]() -
-![]() rot
rot![]() /14.4/
/14.4/
5.Обчислюємо ротор добутку
двох векторів rot
![]() .
Його х – компонента дорівнює:
.
Його х – компонента дорівнює:
rot
х
![]() =
=
![]()
![]() z
-
z
-
![]()
![]() y
=
y
=
![]() (AxВy
- AyВx)
-
(AxВy
- AyВx)
-
![]() (AzВx
- AxВz)
=
(AzВx
- AxВz)
=
![]() Вy +
Вy +
+ Ax
![]() -
-![]() Вx
- Ay
Вx
- Ay
![]() -
-
![]() – Az
– Az
![]() +
+![]() Вz
+ Ax
Вz
+ Ax
![]() = Ax
= Ax
![]() + Ax
+ Ax
![]() +
+
+ Ax
![]() - Ax
- Ax
![]() -
Ay
-
Ay
![]() – Az
– Az
![]() -Вx
-Вx
![]() - Вx
- Вx
![]() -
Вx
-
Вx
![]() + Вy
+ Вy
![]() + Вz
+ Вz
![]() =
=
=
Ax
div
![]() - Вx
div
- Вx
div![]() + (Вx
+ (Вx
![]() + Вy
+ Вy
![]() + Вz
+ Вz
![]() )
Ax –
(Ax
)
Ax –
(Ax
![]() +
Ay
+
Ay
![]() + Az
+ Az
![]() )
Вx
=
)
Вx
=
= Ax
div
![]() - Вx
div
- Вx
div![]() + (
+ (![]() grad)
Ax
– (
grad)
Ax
– (![]() grad)
Вx
grad)
Вx
і тому rot
![]() =
=![]() div
div![]() -
-![]() div
div![]() + (
+ (![]() grad)
grad)![]() - (
- (![]() grad)
grad)![]() /14.5/
/14.5/
6.Знайдемо ротор ротора векторного поля
rot
х rot![]() =
=
![]() rotz
rotz
![]() -
-
![]() roty
roty![]() =
=
![]() (
(![]() -
-
![]() )
-
)
-
![]() (
(![]() -
-
![]() )
=
)
=![]()
![]() -
-![]() -
-
-
![]() +
+![]()
![]() +
+![]()
![]() -
-![]() =
=![]() (
(![]() +
+![]() +
+![]() )
– (
)
– (![]() +
+![]() +
+![]() )
=
)
=
-54-
= grad x
div![]() -
-![]() Ax
Ax
Звідси робимо висновок, що
rot rot![]() = grad div
= grad div![]() -
-![]()
![]() /14.6/
/14.6/
Мислення можна назвати продуктивним, якщо приводить до розв’язку даної конкретної задачі; мислення можна назвати творчим, якщо воно створює засоби для розв’язання майбутніх задач.
Д. Пойа
15.Соленоїдальні поля
Ми будемо говорити про окремий клас векторних полів, дивергенція яких дорівнює нулеві
div
![]() = 0
= 0
Це поля, що не мають джерел, їх називають соленоїдальними.
В соленоїдальному полі
векторні лінії вектора![]() не можуть ніде ні починатися, ні
закінчуватися. Вони можуть іти в
нескінченність або бути замкненими.
не можуть ніде ні починатися, ні
закінчуватися. Вони можуть іти в
нескінченність або бути замкненими.
Нехай
 div
div
![]() = 0
= 0
тоді, згідно з теоремою Остроградського-Гауса
![]()
![]() d
d
![]() =
=![]() div
div![]()
![]() V
= 0
V
= 0
Якщо S – поверхня векторної
трубки, обмеженою циліндроподібною
поверхнею
![]() ,
твірними якої є векторні лінії і основи
,
твірними якої є векторні лінії і основи![]()
![]() і
і![]() ,
тоді
,
тоді
![]()
![]()
![]()
![]() = 0 (
= 0 (![]()
![]()
![]() )
)
Отже,
-55-
![]()
![]() d
d
![]() +
+![]()
![]() d
d![]() = 0
= 0
Змінимо на протилежний напрям
нормалі до поверхні
![]() ,
тоді
,
тоді
![]()
![]() d
d
![]() =
=![]()
![]() d
d![]() /15.2/
/15.2/
Таким чином, потік соленоїдального вектора через будь-який поперечний переріз векторної трубки має ту саму величину.
Згадаємо тепер, що дивергенція ротора векторного поля завжди дорівнює нулеві.
div
rot
![]() = 0
= 0
Якщо векторне поле
![]() (x,y,z)
соленоїдальне
(x,y,z)
соленоїдальне
div
![]() = 0
= 0
то ми завжди можемо представити
вектор
![]() ,
як ротор якось поля
,
як ротор якось поля![]()
![]() =
rot
=
rot![]()
Задача 1. Довести, що добуток
![]()
![]() =
=![]() є соленоїдальним вектором
є соленоїдальним вектором![]() = rot
= rot![]()
Маємо
![]() =
=
![]()
![]() -
-
![]()
![]()
![]()
![]() =
=
![]() (
(![]()
![]() )
-
)
-
![]() (
(![]()
![]() )
=
)
=
![]()
![]() -
-
![]()
![]()
і відповідно
![]() = rot
= rot![]()
Задача 2. Вектор r![]() - соленоїдальний.
- соленоїдальний.
Довести що r![]() = rot
= rot![]() ,
,![]() =
=![]()
Поняття про соленоїдальні
векторні поля вводиться в зв’язку з
законами електромагнетизму. Відомо, що
не існує магнітних зарядів і тому поле
індукції магні тного поля
![]() не має джерел:
не має джерел:
div
![]() = 0
= 0
Це в свою чергу означає, що
можна ввести вектор
![]() такий, що
такий, що
![]() =
rot
=
rot![]()
Вектор
![]() називають вектор-потенціалом магнітного
поля. Магнітне поле породжується
електричними струмами. Якщо заданий
розподіл цих струмів, то можна підрахувати
вектор
називають вектор-потенціалом магнітного
поля. Магнітне поле породжується
електричними струмами. Якщо заданий
розподіл цих струмів, то можна підрахувати
вектор![]() /
який, взагалі кажучи, не має
/
який, взагалі кажучи, не має
-56-
прямого фізичного змісту/ і
тоді легко підрахувати компоненти
вектора
![]() як проекції ротора вектора
як проекції ротора вектора![]() .
.
Приклад. Розглянемо нескінченний прямолінійний провідник, по якому проходить сталий струм.
Підрахунок показує, що компоненти вектора індукції магнітного поля дорівнюють
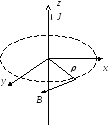
![]()
![]()
![]() ,
,
![]()
Легко бачити, що поле
![]() соленоїдальне
соленоїдальне

Вектор-потенціал
![]() має компоненти
має компоненти
![]() ,
, ![]()
Дійсно
![]()
![]()
![]()
-57-
ТЕНЗОРНИЙ АНАЛІЗ
Три великі лиха довелось мені побороти в житті: граматику, бідність і жінку. Працьовитість визволила мене від першого, невимогливість – від другого, але супружі вузи ще й сьогодні прив’язують мене до третього.
Сократ
16. Косокутні системи координат. Узагальнені проекції та узагальнені складові вектора. Дуальна система координат.
Дотепер ми мали справу тільки з прямокутними декартовими системами координат. Введемо більш загальні – косокутні системи, в яких координатні осі не є перпендикулярними.
Косокутну систему координат
у просторі задають трьома не компланарними
векторами
![]() ,
,![]() ,
,![]() ,які
визначають напрямки трьох осей.
,які
визначають напрямки трьох осей.
Розглянемо у цій системі
вектор![]() .
На відміну від декартових координат,
його проекції і
.
На відміну від декартових координат,
його проекції і
с




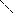

 кладові
тепер не збігаються.
кладові
тепер не збігаються.
Ортогональна проекція вектора
![]() на вісь х дорівнює
на вісь х дорівнює
![]() =
=
![]() =
=![]()
і взагалі
Рис. 57
![]() =
=![]() К=1,2,3. /16.1/
К=1,2,3. /16.1/
Поруч з проекціями
![]() введемо складові вектора
введемо складові вектора![]() /позначимо їх індексом звершу/ і визначимо
їх за формулою
/позначимо їх індексом звершу/ і визначимо
їх за формулою
![]() =
=
![]() +
+![]() +
+![]()
тобто
![]() =
=
![]()
Очевидно, що у випадку прямокутних координат
![]() =
=
![]()
Маючи на увазі подальший
перехід до криволінійних координат,
узагальнимо попередні означення:
припустимо, що для різних осей
![]() ми користуємось різними масштабами,
тобто, замість одиничних векторів
ми користуємось різними масштабами,
тобто, замість одиничних векторів![]() ,
,![]() ,
,![]() введемо масштабні вектори
введемо масштабні вектори![]() напрямки яких
напрямки яких
-58-
відповідно збігаються з
![]() ,
,![]() ,
,![]() ,
тобто
,
тобто

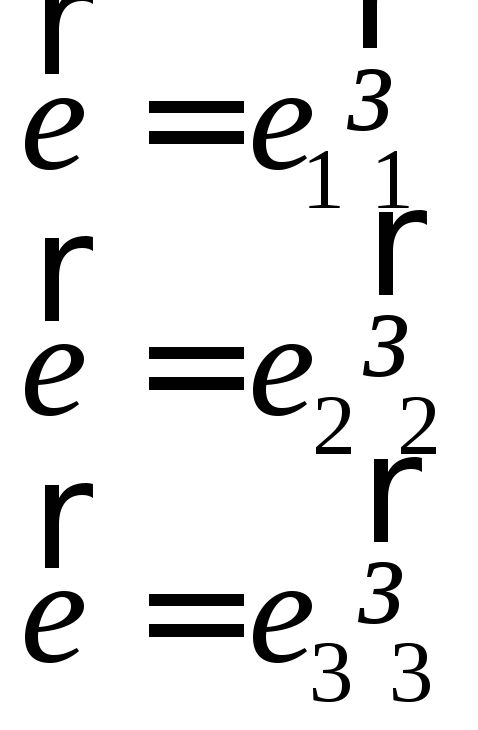 /16. 3/
/16. 3/
Введемо тепер узагальнені
проекції
![]() і узагальнені складові
і узагальнені складові![]() за аналогією /16.1/ і /16.2/
за аналогією /16.1/ і /16.2/
![]() =
=
![]()
![]() /16.4/
/16.4/
![]() /16.5/
/16.5/
Порівнюючи /16.4/ з /16.5/ і /16.5/ з /16.2/ бачимо що
![]() =
=
![]()
![]()
![]() /16.6/
/16.6/
Поруч з масштабними векторами
![]() будемо розглядати систему трьох нових
векторів
будемо розглядати систему трьох нових
векторів![]() ,
визначених рівностями
,
визначених рівностями
![]() /16.7/
/16.7/
З означення випливає
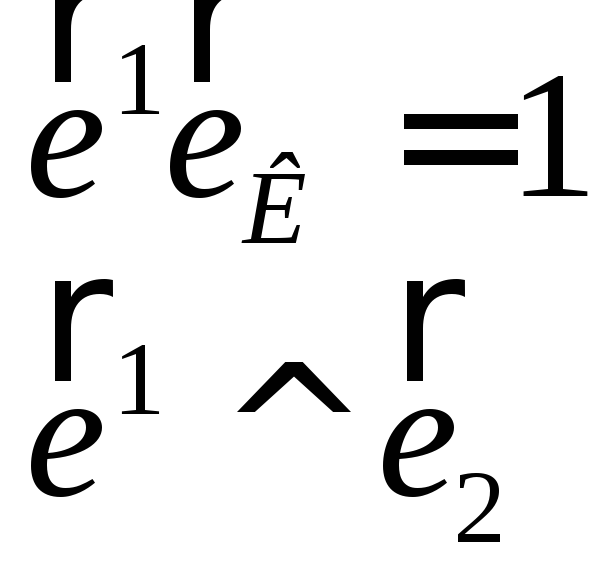

де
![]() - поки що невідомий коефіцієнт. Помножимо
скалярно останню рівність на
- поки що невідомий коефіцієнт. Помножимо
скалярно останню рівність на![]() ,
одержуємо
,
одержуємо
![]()
Звідси
![]()
Де V - об’єм паралелепіпеда,
побудованого на масштабних векторах
![]() .
Таким чином,
.
Таким чином,
![]()
І взагалі
![]() (i,k,l) /16.9/
(i,k,l) /16.9/
Тут (i,k,l) означає, що для індексів i,k,l діє правило циліндричної перестановки, очевидне з наведеної таблиці. Перший рядок таблиці відповідає
|
i |
k |
l |
|
1 |
2 |
3 |
|
2 |
3 |
1 |
|
3 |
1 |
2 |
 59-
59-Рисункові 59, два інші – отримуємо, повертаючи не
заштрихований
диск на
![]() і на
і на![]() .
.
Вектори
![]() називають
взаємними до
називають
взаємними до![]() ,
або дуальними до
,
або дуальними до![]() .
Осі, що їх визначають вектори
.
Осі, що їх визначають вектори![]()
утворюють нову косокутну систему координат, яку називають взаємною або дуальною.
Теорема. В дуальній системі координат роль узагальнених проекцій вііграють узагальнені складові і навпаки.
Доведення. Треба довести, що поруч з відомими формулами
![]() =
=
![]()
![]() /16.4/
/16.4/
![]() К=1,2,3 /16.5/
К=1,2,3 /16.5/
справджуються формули
![]() /16.10/
/16.10/
![]() /16.11/
/16.11/
Помножимо скалярно на
![]() рівність
/16.5/. Одержуємо
рівність
/16.5/. Одержуємо
![]()
і рівність /15.10/ доведена.
Аналогічно, перемножуючи /16.11/ на
![]()
![]()
![]()
ми приходимо до /16.4/, отже вихідна рівність /16.11/ є правильною.
Повернемось до дуальної
системи координат
![]() .
З /16.9/ видно, що
.
З /16.9/ видно, що
 вектор
вектор![]() перпендикулярний до площини, визначеної
векторами
перпендикулярний до площини, визначеної
векторами![]() (к,і
(к,і![]() 0).
0).
Якщо врахувати, що
![]()
де
![]() -
висота паралелепіпеда,
-
висота паралелепіпеда,![]() - площа паралелограма, побудованого на
векторах
- площа паралелограма, побудованого на
векторах![]() то ми побачимо, що
то ми побачимо, що
-60-
![]() (16.12)
(16.12)
- довжина дуального вектора є величиною, оберненою до відповідної висоти паралелепіпеда, побудованого на масштабних векторах.
Знайдемо ще формули, що дають змогу виразити масштабні вектори через дуальні. Будемо виходити з формули
![]()
![]()
і обидві її сторони помножити
векторно на
![]()
![]()
Далі використаємо (3.17)
![]()
![]()
![]() .
.
Таким чином,
![]()
![]() (16.13)
(16.13)
Одержана формула не має
вартості, тому що об’єм V виражений
через масштабні вектори. Тому пору з
об’ємом
![]() введемо об’єм
введемо об’єм
![]() (16.14)
(16.14)
об’єм паралелепіпеда на дуальних векторах.
Переконаємось, що
![]() (16.15)
(16.15)
Для цього використаємо тотожність Лагранжа (3.20), тоді

Формулу (16.13) можемо тепер записати
![]() , (i,l,k)
, (i,l,k)
або в більш зручному вигляді
![]() .
(i,k,l) (16.16)
.
(i,k,l) (16.16)
Введення масштабних векторів у математиці, як було сказано вище, пов’язане з визначенням криволінійних координат (див. 28). Доцільність введення дуальних векторів стане очевидною в наступному параграфі.
-61-
У фізиці введення косокутних
координат з неодиничними масштабами
виявляється дуже зручним, наприклад, у
теорії твердого тіла. Просту просторову
гратку кристала можна охарактеризувати
основними векторами гратки
![]() .
Тоді довільний вузол гратки визначають
„вектором гратки”
.
Тоді довільний вузол гратки визначають
„вектором гратки”
![]() ,
,
де
![]() –
цілі числа. Поруч з основною граткою
–
цілі числа. Поруч з основною граткою![]() розглядають обернену гратку, визначену
векторами
розглядають обернену гратку, визначену
векторами![]()
![]()
і вводять вектор оберненої гратки
![]()
(![]() –цілі
числа). Введення цього вектора пов’язане
з важливою теоремою теорії твердого
тіла – теоремою Влоха
–цілі
числа). Введення цього вектора пов’язане
з важливою теоремою теорії твердого
тіла – теоремою Влоха
Брешуть раби, вільні люди
говорять правду
Сенека
17. Метричний тензор у косокутних координатах
Знайдемо формули переходу від узагальнених складових до узагальнених проекцій і навпаки.
Помножимо рівність
![]()
скалярно на
![]() ,
тоді
,
тоді
![]() (17.1)
(17.1)
Введемо позначення
![]() (17.2)
(17.2)
Дев’ять величин
![]() бедемо називати складовими метричного
тензора. Якщо
бедемо називати складовими метричного
тензора. Якщо![]() ,
то
,
то
![]() ,
,
![]() (17.3)
(17.3)
величини
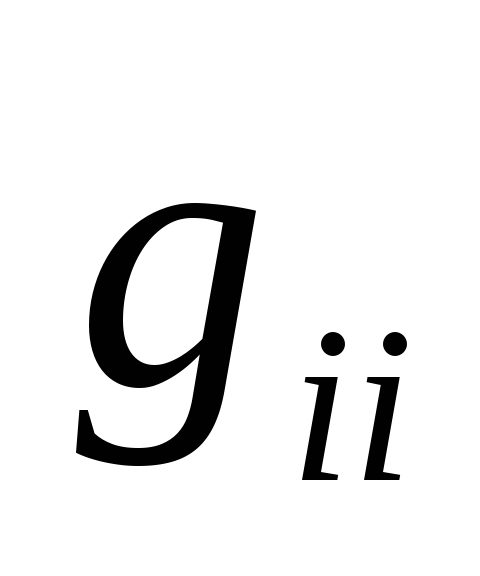 характеризують довжини відповідних
масштабних векторів. При
характеризують довжини відповідних
масштабних векторів. При
![]() (17.4)
(17.4)
величини
![]() визначають
прямокутну матрицю
визначають
прямокутну матрицю
-62-
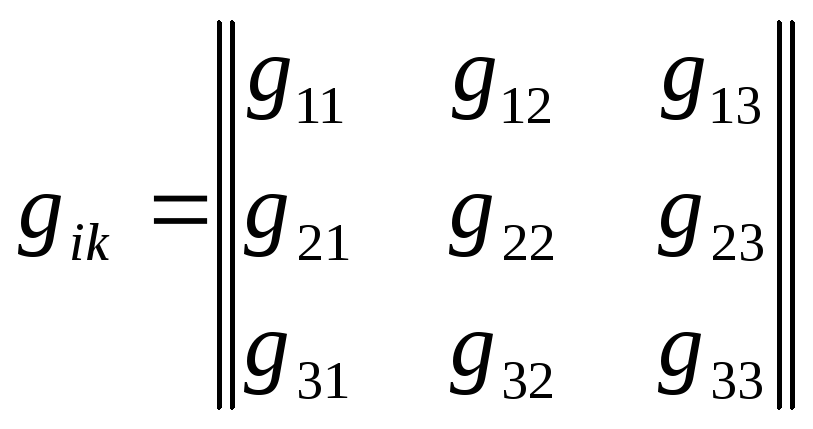
![]() (17.5)
(17.5)
однак, з дев’яти елементів
![]() істотно різних є тільки шість. Це тому,
що
істотно різних є тільки шість. Це тому,
що
![]() (17.6)
(17.6)
Геометричний зміст величини
![]() полягає в тому, що вони є узагальненими
проекціями масштабних векторів на самих
себе.
полягає в тому, що вони є узагальненими
проекціями масштабних векторів на самих
себе.
Якщо масштабні вектори
одиничні, то
![]() –
просто косинуси кутів між осями
координатної системи. Зокрема, для
прямокутної системи координат
–
просто косинуси кутів між осями
координатної системи. Зокрема, для
прямокутної системи координат
![]() ,
,  (17.7)
(17.7)
Приклад. Плоска косокутна система задана масштабними векторами
![]()
![]() ,
,
що утворюють кут
![]() .
.
Компоненти метричного тензора тоді визначають матрицю
![]()
Повернемось до формули (17.1).
використовуючи вирази
![]() можемо написати
можемо написати
![]() ,
,
тобто
![]() ,
,
![]() (17.8)
(17.8)
Ця група формул дозволяє знати унікальні проекції вектора, якщо відомі його узагальнені складові і компоненти метричного тензора.
Розглянемо тепер формулу
![]() .
.
Обидві її сторони помножимо
скалярно на
![]()
![]() .
(17.9)
.
(17.9)
Введемо дев’ять величин
-63-
![]() ,
,
![]() . (17.10)
. (17.10)
які також будемо називати компонентами метричного тензора. Надалі
![]() будемо називати коваріантним складовим
матеріального тензора,
будемо називати коваріантним складовим
матеріального тензора,
![]() –
його контраваріантним складовими. Сенс
цих термінів стане зрозумілим пізніше.
–
його контраваріантним складовими. Сенс
цих термінів стане зрозумілим пізніше.
Формулу (17.9) можна записати
![]() .
. ![]() (17.11)
(17.11)
Дев’ять величин
![]() (чи
відповідно
(чи
відповідно![]() )
характеризують метрику косокутного
простору. Якщо задана матриця
)
характеризують метрику косокутного
простору. Якщо задана матриця![]() є
діагональною, тобто
є
діагональною, тобто
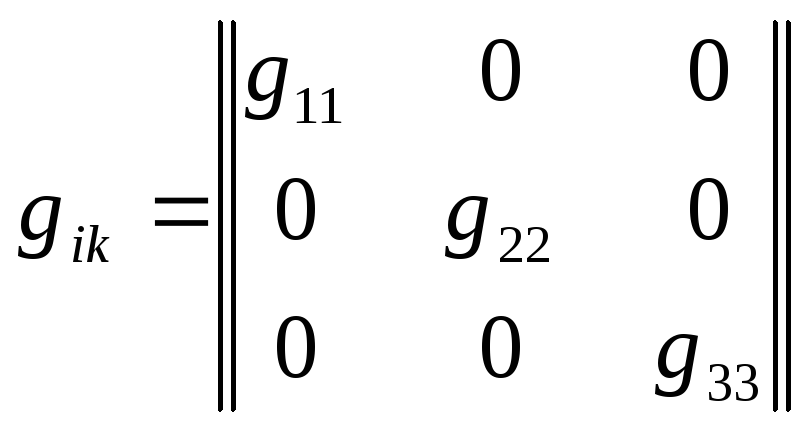
то зрозуміло, що система прямокутна (але масштаби не обов’язково одиничні ).
Таким чином, косокутну систему
координат можна задати трьома масштабними
векторами
![]() ,
або дев’ятьма (точніше–шістьма)
величинами
,
або дев’ятьма (точніше–шістьма)
величинами![]() .
Зв’язок між
.
Зв’язок між![]() і
і![]() задають формулами (17.2) і (17.3)
задають формулами (17.2) і (17.3)
Знайдемо групу формул, які зв’язують масштабні вектори в дуальними через складові метричного тензора. Будемо виходити з рівності
![]() .
.
Замість
![]() підставимо
сюди вираз (17.8).
підставимо
сюди вираз (17.8).
![]() .
.
Звідси випливе, що
![]() ,
, ![]()
або в більш конкретному записі
![]() .
. ![]() (17.12)
(17.12)
Аналогічно знайдемо
![]() ,
,
![]() (17.13)
(17.13)
Таким чином, ми маємо три групи формул, що зв’язують масштабні і дуальні вектори
-64-
![]() =
=![]() i,k=1,2,3 /1/
i,k=1,2,3 /1/
![]() =
=![]() ,
,![]() =
=![]() (I,k,c) /2/
(I,k,c) /2/![]() =
=![]() ,
,![]() =∑
=∑![]() i=1,2,3 /3/
i=1,2,3 /3/
Найбільшим ступенем невігластва є фальшива наука.
Алі бен Марабу
10. Скалярний і векторний добуток двох векторів в косокутних координатах.
Розглянемо два вектори А⃗=![]() ,
В⃗=
,
В⃗=![]()
І обчислюю їх скалярний
добуток А⃗В⃗=
∑і ∑к ![]() =∑і
∑к
=∑і
∑к![]()
Якщо врахувати, що ∑к![]()
А⃗В⃗=∑i![]()
Вектори А⃗
і В⃗ можна
записати також у вигляді А⃗=![]() ,
В⃗=
,
В⃗=![]()
Тоді А⃗В⃗=
∑і ∑к ![]() =∑і
∑к
=∑і
∑к![]() ,
,
А тому, що ∑к![]()
То справедлива також формула
А⃗В⃗=∑i![]()
Таким чином, для скалярного добутку двох векторів у косокутних координатах маємо чотири формули
А⃗В⃗=
∑і ∑к![]() /18.1/
/18.1/
-65-
А⃗В⃗=
∑і ∑к![]() ,
/18.2/
,
/18.2/
А⃗В⃗=∑i![]() /18.3/
/18.3/
А⃗В⃗=∑i![]() /18.4/
/18.4/
Розглянемо тепер вираз для векторного добутку векторів А⃗ і В⃗
![]() =∑і
∑к[
=∑і
∑к[![]() .
.
З дев'ятки доданків у цій подвійній сумі
три доданки дорівнюють нулеві. Дійсно,
[ ![]() 0
і=к
0
і=к
Далі маємо [![]() -[
-[![]() ],
],
Отже ![]() =
=![]() (
(![]() )
/18.5/
)
/18.5/
Правильність такого запису перевіряють
безпосередньо. Розглянемо два з шести
доданків ![]() ]
]![]() +[
+[![]() ]
]![]() =
=![]() ](
](![]()
Тому
![]() =
=![]() ](
](![]() +[
+[![]() ](
](![]() +[
+[![]() ](
](![]() .
/18.6/
.
/18.6/
Якщо згадаємо формулу [ ![]() V
V![]() ,
(I,k,c)
,
(I,k,c)
То маємо ще один запис векторного добутку в косокутих координатах
![]() =
=![]() (
(![]() )
/ 18.7/
)
/ 18.7/
або в розгорнутому вигляді
![]() =
=![]() (
(![]() +V
+V![]() (
(![]() +
+![]() (
(![]() .
/18.8/
.
/18.8/
Запишемо ще раз формулу для скалярного
добутку векторів ![]()
А⃗В⃗=∑і
∑к ![]() \
\
І врахуємо , що ![]()
Тоді А⃗В⃗=∑к![]() =
=![]() .
.
-66-
З другого боку ![]() =
=![]()
отже, повинна задовольнятися рівність
![]() =
=![]() I,l=1,2,3
/18.9/
I,l=1,2,3
/18.9/
Де ![]() -
символ Кронекера / ми вводимо нове
позначення
-
символ Кронекера / ми вводимо нове
позначення![]() замість
замість![]() ,доцільність
такого поняття стане зрозумілою в
наступному параграфі/.
,доцільність
такого поняття стане зрозумілою в
наступному параграфі/.
Формули /18.9/ встановлюють зв'язок між
коваріантними і контрваріантними
складовими матричного тензора. Якщо
відомі коваріантні складові ![]() , то /18.9/ можна розглядати як систему
лінійних алгебраїчних рівнянь для
визначення
, то /18.9/ можна розглядати як систему
лінійних алгебраїчних рівнянь для
визначення![]()
І=1 l=1 ![]()
I=1 l=2 ![]() ,
і т.д.
,
і т.д.
Згідно з теоремою Крамера розв'язки цієї системи дорівнюють
![]() =
=![]() ,
/18.10/
,
/18.10/
Де g=dct /![]() -детермінант
, підрахований з елементів матриці
-детермінант
, підрахований з елементів матриці![]() .
.
Переконаємось , що g=![]() /18.11/
/18.11/
Де V- об’єм паралелепіпеда , побудованих на масштабних векторах. Використовуючи тотожність Лагранжа одержуємо
![]() =
(
=
(![]() [
[![]() ])(
])(![]() ])=
])= =dct
=dct![]() =g
=g
![]() =(
=(![]() [
[![]() ])(
])(![]() ])=
])= =det/
=det/![]() .
.
-67-
Уява важливіша від знань.
А. Ейнштейн
19. Правила індексів
Запишемо ще раз окремі формули , одержані в попередніх параграфах:
![]() ,
(𝛼)
,
(𝛼)![]() ,
/𝛾/
,
/𝛾/![]() ,
(𝛽)
,
(𝛽)![]() ,
/𝛿/
,
/𝛿/
А⃗В⃗=∑і
∑ ![]() =
∑і ∑
=
∑і ∑![]() /𝜀/
/𝜀/
Якщо уявно придивитись до цих формул,як і зрештою до всіх інших формул попередніх трьох параграфів,то можна завважити певні законо-мірності для індексів у формулах . Таких закономірностей є чотири.
1.Якщо якийсь індекс фігурує в лівій стороні формули один раз, то він фігурує в правій стороні формули також один раз. Якщо зліва індекс знаходиться знизу ,то і в правій стороні формули цей індекс знаходиться знизу. Якщо індекс знаходиться зверху, то він знаходиться зверху в обох сторонах формули . Такий індекс називають рухомим індексом,його можна позначити довільною буквою.
Прикладами на це правило є формули /𝛼-𝛿/,де рухомим індексом є індекс і . Ці ж формули можна записати
![]() ,
,![]() ,
,
![]() ,
,![]() .
m=1,2,3.
.
m=1,2,3.
2.Формула залишається справедливою , якщо в обох її сторонах підняти рухомий індекс знизу вверх. Наприклад, формула (𝛽) одержується підніманням рухомого індекса і в формулі (𝛼).
Справедливе і обернене. Наприклад
, оускаючи два рухомі індекси і,к в
формулі ![]()
Одержемо ![]() I,k=1,2,3 3.
I,k=1,2,3 3.
Якщо якийсь індекс знаходиться під знаком суми, то він зустрічається обов’язково два рази: один раз знизу і один раз зверху. Такий індекс називають німим індексом, його можна позначити довільною буквою.
-68-
Прикладом німого індекса є індекс к в формулі
![]() ,
,
Цю ж формулу можна записати ![]() ,
,
У формулі (𝜀)виступають два німі індекси і,к.
Формула/18.5/ не є винятком з цього правила. Індекс ℓ зв’язаний з індексом і,к правилом циклічної перестановки.
4.Формула залишається справедливою, якщо німий індекс в одному місці опустити і в другому підняти. Наприклад,справедливими є формули
А⃗В⃗=∑i![]() ,
А⃗В⃗=∑i
,
А⃗В⃗=∑i![]() І також формули
І також формули
А⃗В⃗=∑і
∑ ![]() , А⃗В⃗=
∑і ∑
, А⃗В⃗=
∑і ∑![]()
Закономірності і/ -4/ зважив Ейнштейн в 1916 році. Він запропонував правило, яке дозволяє записувати формули в більш простому і компактному виляді / правило підсумовування Ейнштейна/.
Якщо один і той же індекс входить в який-небуть одночлен двічі, один раз зверху, а другий раз знизу, то написаний вираз означає суму одночленів, в яких цей індекс пробігає всі значення від І до 3/в n-вимірному просторі- відІ до n/. Наприклад,
Таким чином, формули /18.1/ - /18.4/ можна записати
А⃗В⃗=
![]() , А⃗В⃗=
, А⃗В⃗=![]() ,.
,.
А⃗В⃗![]() ,
А⃗В⃗=
,
А⃗В⃗=![]()
З другого боку, користуватись правилом Ейнштейна вимагає певни навиків /треба розуміти символ суми там, де він не фігурує/. Тому в нашому курсі цим правилом користуватися не будемо.
Повернемось ще раз до формул ![]() ,
,![]() ,
,
Перша з них визначає правило опускання
індекса: щоб опустити індекс у величині
![]() досить застосувати оперетор
досить застосувати оперетор![]() /19.1/
/19.1/
-69-
Тобто, досить помножити ![]() на коваріантний матричний тензор
на коваріантний матричний тензор![]() і підсумувати по індексу к.
і підсумувати по індексу к.
Аналогічно друга з формул /19.1/ визначає правило піднімання індекса , яке зводиться до множення на контраваріантний матричний тензор і відповідного сумування.
![]() узагальнені проекції і узагальнені
складові вектори. Нехай , наприклад,
маємо вираз
узагальнені проекції і узагальнені
складові вектори. Нехай , наприклад,
маємо вираз![]() . Ми можемо одержати є нього вираз
. Ми можемо одержати є нього вираз![]() опускаючи індекс і.
опускаючи індекс і.![]() =
=![]()
Вчимось на помилках. Є народи,
що вчаться на досягнення .
А. Качановський
20. Диференціальні операції в косокутних координатах.
У косокутній системі координат,визначеній
масштабними векторами ![]()
Р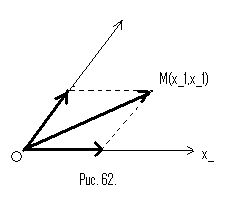 озглянемо
довільну точку з координат
озглянемо
довільну точку з координат![]()
Ці три величини як видно з рис. 62,
/ рисунок правильний якщо вектори
одиничні
/, в узагальненими складовими
радіуса – вектора ![]()
![]() ,
,![]() =
=![]() /20.1/
/20.1/
МИ бачимо ,що позначення ![]() для косокутних координат точки є
невдалими. Для більш конкретного запису
формул треба ввести позачення
для косокутних координат точки є
невдалими. Для більш конкретного запису
формул треба ввести позачення
![]() ,
,![]() ,
,![]() ,
тоді
,
тоді![]() +
+![]() +
+![]()
Нехай в косокутних системах задана функція
φ= φ( x ,y ,z ) =
φ(![]() ,
,![]() ,
,![]() )
)
яка в точці М має значення φ(![]() ,
,![]() ,
,![]() )
і в близькій точці М' – значення
)
і в близькій точці М' – значення
φ=(![]() ,
,![]() ,
,![]() ) = φ(
) = φ(![]() ,
,![]() ,
,![]() )+𝛿φ.
)+𝛿φ.
-70-
З точністю до малих величин вищого порядку
𝛿φ= ![]() 𝛿
𝛿![]() +
+![]() 𝛿
𝛿![]() +
+![]() 𝛿
𝛿![]() =
=![]() .
.
Отриманий вираз можна
інтерпретувати як скалярний добуток
двох векторів А⃗В⃗=∑i![]() ,
,
де ![]()
![]()
Тоді 𝛿φ=![]()
Таким чином , у косокутних координатах величини
![]() =
=![]() /20.2/
/20.2/
Інтерпретуються як узагальнені проекції
градієнта скалярної функції, Символічно
![]() =
=![]() ,
/20.3/
,
/20.3/
![]() =
=![]() +
+![]() +
+![]() .
/20.4/
.
/20.4/
Легко знайти узагальнені складові вектора набла. Для цього досить піднести індекс у величин
![]() =
=![]() /20.5/
/20.5/
Нехай у косокутній системі задане векторне поле
![]()
Щоб знайти вираз для дивергенції
вектора ![]() досить згадати що
досить згадати що
div ![]() =
=![]()
Тоді div ![]() =
=![]() =
=![]() ,
,
div ![]() =
=![]() +
+![]() +
+![]() . /20.6/
. /20.6/
Аналогічно можна знайти вираз для ротора векторного поля в косокутних координатах. Для цього використовують формулу
-71-
rot ![]() = [
= [![]() ]
]
Нам залишається ще знайти вираз для оператора Лапласа в косокутних координатах. Будемо виходити з формули
Δ=![]() . тоді
. тоді
![]() =
=![]() =
=![]() ,
,
І остаточно Δ = ![]()
![]() .
.
У випадку декартової системи ![]() =
=![]() і /20.7/ зводиться до відомого виразу
Δ =
і /20.7/ зводиться до відомого виразу
Δ =![]()
![]() =
=![]() .
.
Метод важливіший від відкриття ,тому що правильний метод дослідження приведе нас до нових , ще більш цінних відкриттів.
Л. Ландау
21. Перетворення координат і компонент вектора при переході від однієї косокутної системи до іншої
Здійснимо перехід від косокутної
системи до ![]() до нової системи
до нової системи
![]() . Простір будемо вважати лінійним , отже
вектори
. Простір будемо вважати лінійним , отже
вектори![]() повинні бути пов’язані лінійними
співвідношеннями
повинні бути пов’язані лінійними
співвідношеннями

![]() =
=![]() , і= 1,2,3 /21.1/
, і= 1,2,3 /21.1/
![]() =
=![]() ,
к = 1,2,3 /21.2/
,
к = 1,2,3 /21.2/
З'ясуємо геометричний зміст коефіцієнтів
![]() і
і![]() . Приймемо в /21.1/ і =1 , тоді
. Приймемо в /21.1/ і =1 , тоді
![]() =
=![]() +
+![]() +
+![]() .
.
Рис. 63 Довільний
вектор ![]() можна розкласти по трьох напрямках
можна розкласти по трьох напрямках![]()
![]() =
=![]() +
+![]() +
+![]() ,
,
-72-
Отже /21.1'/ - це формула розкладу вектора
![]() по напрямках нових масштабних векторів
. Звідси зрозуміло , що
по напрямках нових масштабних векторів
. Звідси зрозуміло , що![]() - це узагальнена складова вектора
- це узагальнена складова вектора![]() по напрямку вектора
по напрямку вектора![]() ,
,![]() -
узагальнена складова вектора
-
узагальнена складова вектора![]() по напрямку
по напрямку![]() .
Взагалі ,
.
Взагалі ,![]() - це узагальнена складова вектора
- це узагальнена складова вектора![]() по напрямку
по напрямку![]() .
.
Аналогічно , ![]() - це узагальнена складова вектора
- це узагальнена складова вектора![]() по напрямку
по напрямку![]() .
.
Розглянемо довільний вектор ![]() і обидві сторони /21.1/ і /21.2/ помножимо
скалярно на
і обидві сторони /21.1/ і /21.2/ помножимо
скалярно на![]() . Маємо
. Маємо
![]() =
=![]() , і= 1,2,3
, і= 1,2,3
![]() =
=![]() ,
к = 1,2,3
,
к = 1,2,3
Тут ![]() =
=![]() - узагальнені проекції вектора у старій
системі,
- узагальнені проекції вектора у старій
системі,
![]() =
=![]() – узагальнені проекції вектора
– узагальнені проекції вектора![]() в новій системі. Таким чином,
в новій системі. Таким чином,
![]() =
=![]() , і= 1,2,3
/21.3/
, і= 1,2,3
/21.3/
![]() =
=![]() ,
к = 1,2,3 /21.4/
,
к = 1,2,3 /21.4/
Формули /21.3/ і /21.4/ дають закон , за яким перетворюються узагаль-нені проекції від однієї косокутної системи до іншої. Іншими словами ,
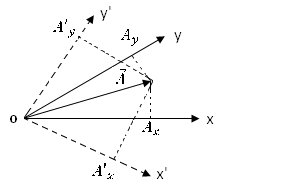 /21.3/ і /21.4/ визначають трансформа-ційні
властивості узагальнених проекцій
вектора.
/21.3/ і /21.4/ визначають трансформа-ційні
властивості узагальнених проекцій
вектора.
Узагальнені проекції вектора будемо називати називати його коваріантними складовими .
На рис. 64 показано як змінюються Рис. 64 коваріантні складові вектора при при переході від однієї системи до іншої . для простоти розглянемо дві плоскі системи , визначені одиничними масштабними векторами .
Знайдемо закон перетворення узагальнених
складових вектора .
У формулу ![]() =
=![]() підставимо /21.1/ . Одержимо
підставимо /21.1/ . Одержимо
-73-
![]() =
=![]() .
.
З другого боку, вектор ![]() можна розкласти по масштабних векторах
нової системи
можна розкласти по масштабних векторах
нової системи![]() =
=![]() .
.
Порівнюючи вирази для ![]() знайдемо
знайдемо
![]() '
=
'
=![]() . к = 1,2,3 /21.5/
. к = 1,2,3 /21.5/
Аналогічно ![]() =
=![]()
![]() '.
і = 1,2,3 /21.6/
'.
і = 1,2,3 /21.6/
Узагальнені складові вектора називають його контраваріантними складовими . Формули /21.5/ і /21.6/ визначають трансформаційні властивості контраваріантних складових вектора .
Легко завважити,що контраваріантні складові вектора перетворюються за іншим законом,ніж його коваріантні складові. Дійсно,розписуючи /21.3/, одержимо.
![]() =
=![]() +
+![]() +
+![]()
![]() =
=![]() +
+![]() +
+![]() /21.3'/
/21.3'/
![]() =
=![]() +
+![]() +
+![]()
А формули /21.6/ мають вигляд
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]()
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() /21.6'/
/21.6'/
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]()
У випадку декартових координат очевидно
![]() =
=![]() ,
,
![]() =
=![]()
І тому ![]() =
=![]() =
=![]() =
=![]() )
.
)
.
Формули /21.1/ і /21.2/ визначають трансформаційні властивості масштаб-них векторів . Знайдемо подібні формули для дуальних векторів. Для цього досить записати /21.5/ і /21.6/ у вигляді
![]() =
=![]()
![]() , і =1,2,3
, і =1,2,3
![]() =
=![]()
![]() , к =1,2,3 а звідси випливає , що
, к =1,2,3 а звідси випливає , що
-74-
![]() =
=![]()
![]() к =1,2,3 /21.7/
к =1,2,3 /21.7/
![]() =
=![]()
![]() і =1,2,3 /21.8/
і =1,2,3 /21.8/
У формулі /21.8/ пере позначимо рухомий і німий індекс
![]() =
=![]()
![]()
І розглянемо добуток ![]() . використовуючи /21.1/ одержимо
. використовуючи /21.1/ одержимо
![]() =
=![]()
![]()
![]() .
.
Тут ![]() =
=![]() ,
,![]()
![]() =
=![]() ,
,
Отже , ![]() =
=![]() =
=![]() .
.
Таким чином , коефіцієнти ![]() і
і![]() не є незалежними - вони пов’язані
дев'ятьма співвідношеннями
не є незалежними - вони пов’язані
дев'ятьма співвідношеннями
![]() =
=![]() . і,ι = 1,2,3 /21.9/
. і,ι = 1,2,3 /21.9/
Цю рівність можна записати і в іншому вигляді . виходячи з формул /21.7/ і /21.2/ , маємо
![]() =
=![]()
![]() ,
,![]() =
=![]()
![]()
![]()
![]() =
=![]()
![]() =
=![]() ,
,
А пере позначуючи індекс одержимо
![]() =
=![]() і,ι = 1,2,3
/21.10/
і,ι = 1,2,3
/21.10/
У випадку декартових координат ![]() =
=![]() =
=![]() і ми приходимо до формул /1.12/ і /1.10/ .
і ми приходимо до формул /1.12/ і /1.10/ .
На випадковість при великих відкриттях
натрапляють лише ті , хто її вартий .
Ж. Лагранж
22. Скаляри , вектори і тензори в косокутній системі координат
У математиці і фізиці розрізняють дві групи величин : інваріантні і варіантні.
-75-
Інваріантом /скаляром/ називають величину , яка не змінюється при переході від однієї системи координат до іншої. Приклади : дивергенції вектора , скалярний добуток двох векторів , температура тіла та ін.
Варіантні величини – це величини , що змінюються за певним законом при переході від однієї системи координат до іншої. Варіантними величинами є компоненти вектора , а також більш складні величини – компоненти тензора.
Означення :Три величини ![]() називаються коваріантними складовими
вектора , якщо при переході від однієї
косокутної системи до іншої вони
перетворюються за законом
називаються коваріантними складовими
вектора , якщо при переході від однієї
косокутної системи до іншої вони
перетворюються за законом
![]() =
=![]() , і = 1,2,3 /22.1/
, і = 1,2,3 /22.1/
![]() =
=![]() , к= 1,2,3 /22.2/
, к= 1,2,3 /22.2/
Означення2:Три величини ![]() називаються
коваріантними скла-довими вектора ,
якщо при переході від однієї косокутної
системи до іншої вони перетворюються
за законом
називаються
коваріантними скла-довими вектора ,
якщо при переході від однієї косокутної
системи до іншої вони перетворюються
за законом
![]() =
=![]() , к = 1,2,3
/22.3/
, к = 1,2,3
/22.3/
![]() =
=![]() , і= 1,2,3
/22.4/
, і= 1,2,3
/22.4/
Таким чином , вектор має три коваріантні і три контрваріантні складові. Вони пов’язані між собою за допомогою матричного тензора.
![]() =
=![]()
![]() =
=![]() і = 1,2,3 /22.5/
і = 1,2,3 /22.5/
Очевидно , в декартовій системі координат
![]() =
=![]() =
=![]()
![]() =
=![]() .
.
Виявляється , що існують величини
більш складні ніж вектори і їх компоненти
. Розглянемо два вектори ![]() і
і![]() та їх коваріантні складові
та їх коваріантні складові![]() (і =1,2,3) ,
(і =1,2,3) ,![]() = (j = 1,2,3). Утворимо так званий мішаний
добуток
= (j = 1,2,3). Утворимо так званий мішаний
добуток
![]() . і,j =1,2,3
. і,j =1,2,3
Це сукупність дев'яти величин , що перетворюються за певним законом при переході від однієї системи до іншої . Цей закон має вигляд
![]() =
=![]()
![]() тобто
тобто![]() =
=![]()
-76-
![]() Припустимо,
що існують величини, які мають дев’ять
компонент, але не обов’язково є мішаними
добутками. Закон їх перетворення такий:
Припустимо,
що існують величини, які мають дев’ять
компонент, але не обов’язково є мішаними
добутками. Закон їх перетворення такий:

![]()
(22.7)
![]() такі
девять величин називають коваріантними
складовими тензора другого рангу.
такі
девять величин називають коваріантними
складовими тензора другого рангу.
Формули зворотнього перетворення для коварінтних складових тензора другого рангу знайдемо виходячи з формул

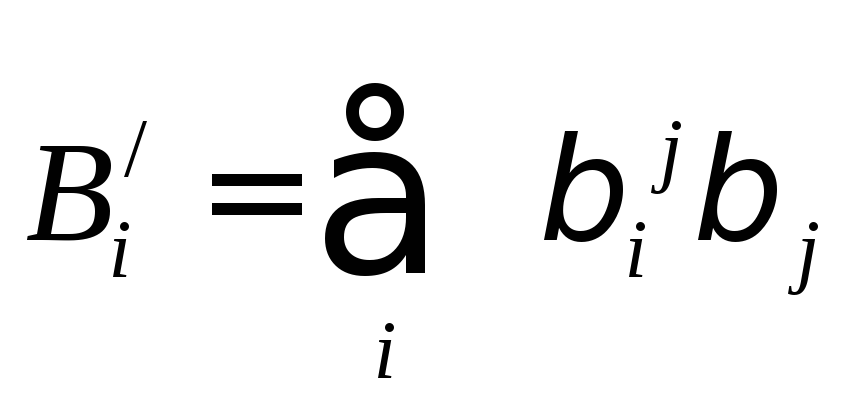
Тоді

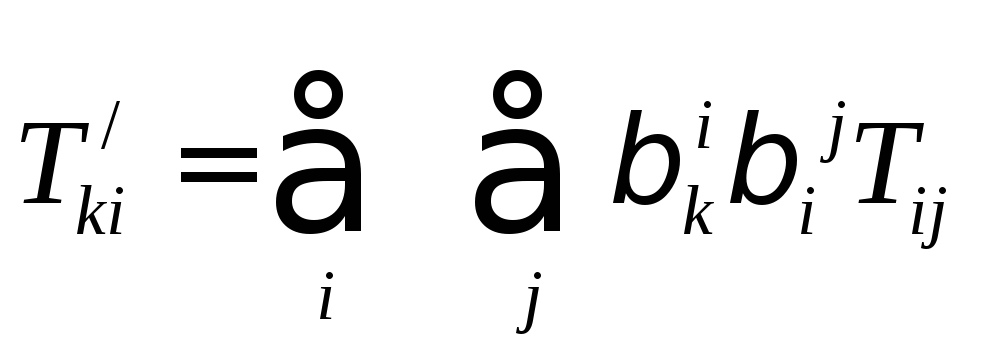
к,і=1,2,3 (22.8)
Поняття
тензора є більш складним ніж поняття
вектора. Вектор можна інтерпретувати
геометрично як відрізок, що має довжину
і напрям, або зобразити його як рядок з
його компонент![]() Тензор другого рангу можна представити
з допомогою матриці
Тензор другого рангу можна представити
з допомогою матриці
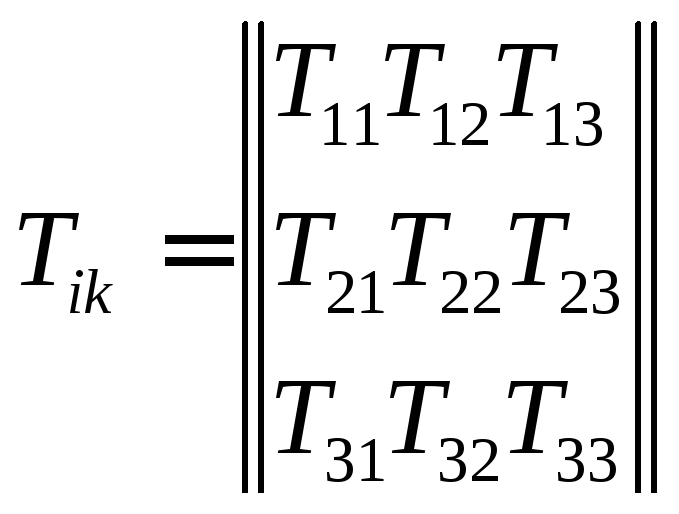 (22.9)
(22.9)
Розглянемо мішані добутки контраваріатних складових двох векторів Аі і Вj , для яких закон перетворення має вигляд
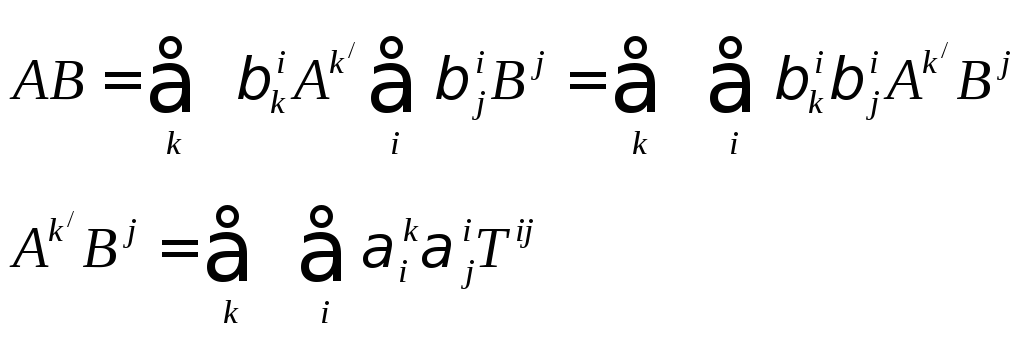
і,j=1,2,3 (22.10)
к,і=1,2,3 (22.11)
Аналогічно можна про дев’ять величин Ті j, які мають такий же закон перетворення
Будемо їх називати котраваріантними складовими тензора другого рангу. Вони визначають матрицю

-77-
Нарешті, за аналогію з мішаним
добутком Аі
Вj ,
можна говорити про мішані компоненти
тензора другого рангу![]() ,
їх трансформаційні властивості мають
вигляд
,
їх трансформаційні властивості мають
вигляд
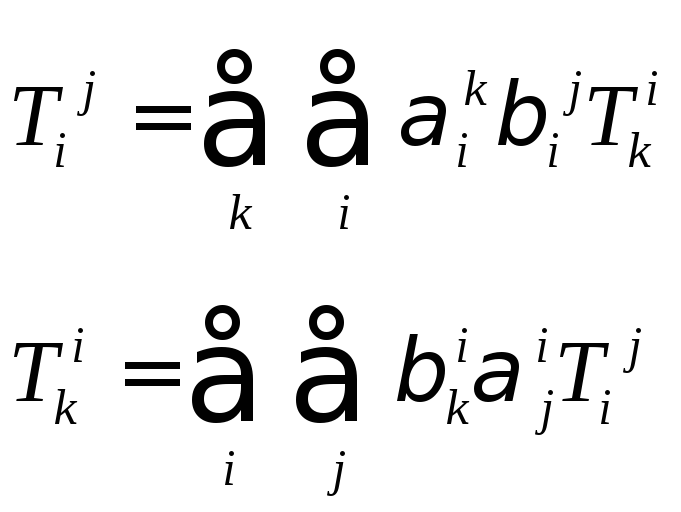
і,j=1,2,3 (22.12)
к,і=1,2,3 (22.13)
Таким чином, тензор другого
рангу маэ девять коварыантних складових
Тij , дев’ять контраваріатних складових
Ті j і дев’ять мішаних складових
![]() .
Зв’язок між ними здійснюється за
допомогою операцій опускання і піднімання
індексів
.
Зв’язок між ними здійснюється за
допомогою операцій опускання і піднімання
індексів
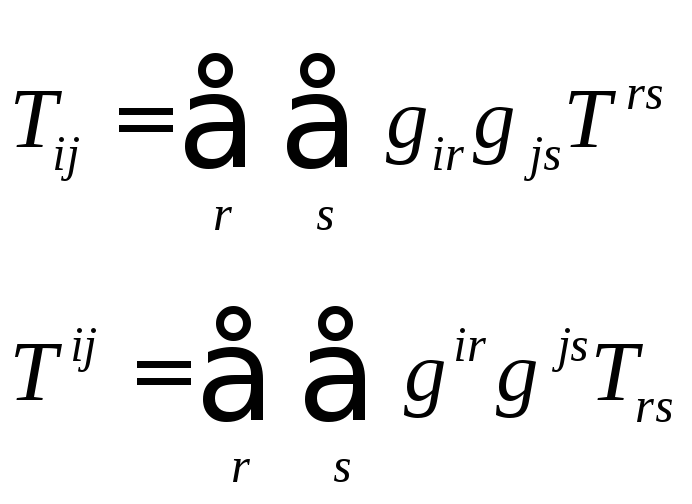
Застосовуючи цю операцію два рази, ми можемо написати
Зауважимо, що при опусканні чи підніманні
індексів тензора потрібна обережність.
Опускаючи в тензора
![]() індекс
S одержимо мішаний тензор
індекс
S одержимо мішаний тензор![]() опускаючи
індекс r одержимо мішаний тензор
опускаючи
індекс r одержимо мішаний тензор![]() .
При цьому, взагалі кажучи,
.
При цьому, взагалі кажучи,
![]()
Власне тому доцільно, місце, з якого опущено індекс, позначати точкою. Виняток становлять симетричні тензори, коли порядок індексів не має значення. Очевидно, що аналогічно спостерігається і при підніманні індексів коваріантних складових тензора
![]()
Тепер можна ввести поняття про тензори третього і вищих рангів. Трансформаційні властивості складових тензора третього рангу визначаються за формулами
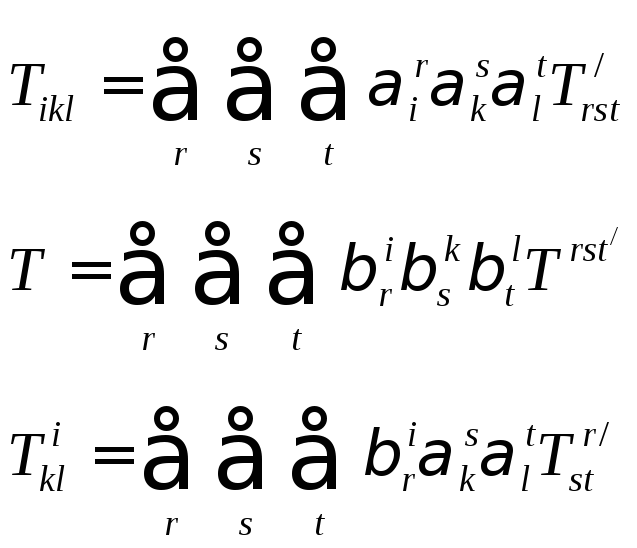
-78-
Зв'язок між ко- і котривіальними складовими здійснюється за допомогою операцій опускання і піднімання індексів.
Даємо тепер загальне ьозначення:
Тензором рангу N, що має N1 коваріантних і N2 коваріантних складових / N1+ N2= N/, називають сукупністю 3N величин, які при переході від однієї косокутної системи до іншої перетворюються за законом
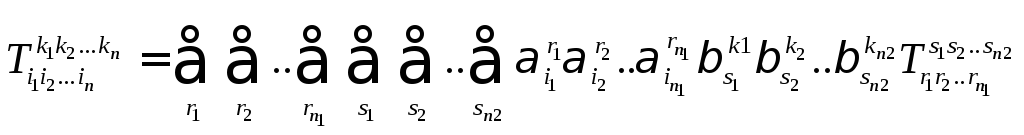
Кількість коваріантних чи контрваріантних індексів можна змінювати за допомогою операцій спускання чи піднімання індексів.
Наприклад,
![]()
Згідно з загальним означенням, вектор можна трактувати, як тенвектор рангу N1, скаляр – як тензор рангу N = 0.
Перерахуємо деякі загальні властивості тензорів:
1/ добуток тензора на стале число є тензором цього ж рангу;
2/ сума двох тензорів є також тензором цього ж рангу
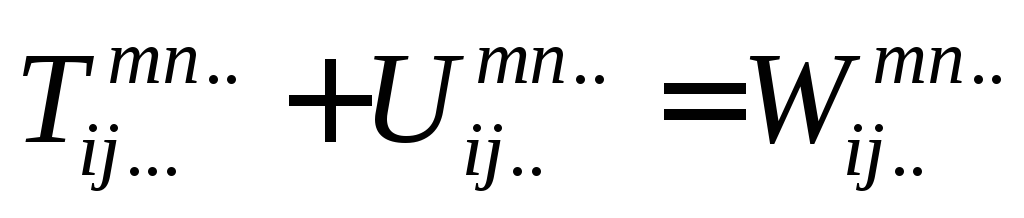
Очевидно, що обидва доданки повиння мати однакову кількість верхніх індексів і відповідно однакову кількість нижніх індексів, тобто обидва доданки повинні мати однакову тензорну розмірність;
3/ добуток двох тензорних рангів N і M є тензером рангу N + M.
Перевіримо правильність
цієї теореми для добутку двох тензорів
![]() і
і![]() ,
тобто переконаємось, добуток
,
тобто переконаємось, добуток![]() є мішаним тензором шостого рангу. Для
цього досить записати трансформаційні
властивості тензорів Т і
є мішаним тензором шостого рангу. Для
цього досить записати трансформаційні
властивості тензорів Т і![]()
і тоді
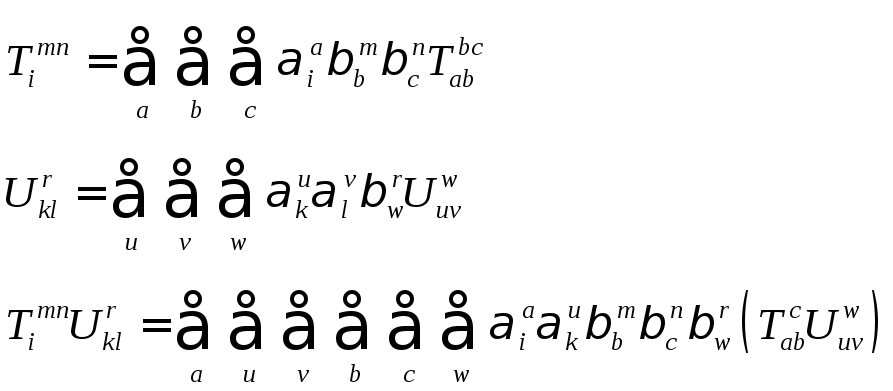
Права сторона цієї рівності і дає закон перетворення мішаного тензора шостого рангу.
Дамо два важливі означення.
Тензор
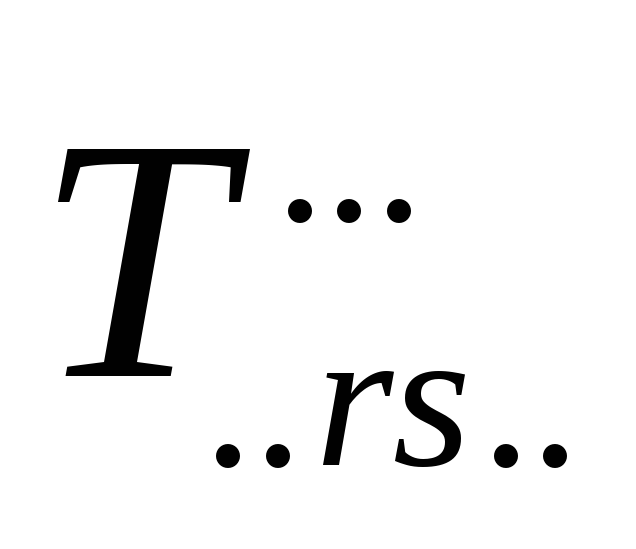 називається
симетричним відносно індексів
називається
симетричним відносно індексів якщо
значення його компонент не змінюється
при перестановці індексів
якщо
значення його компонент не змінюється
при перестановці індексів
-79-
![]()
Зокрема для симетричного тензора другого рангу виконується умова
![]()
2. Тензор
![]() називають
антисиметричним відносно індексів
називають
антисиметричним відносно індексів![]() якщо
якщо
![]()
Компоненти асиметричного
тензора другого рангу задовольняються
умові
![]()
Якщо симетричними є коваріантні складові тензора, то і відповідні контраваріантні складові є симетричними. Наприклад, для тензора другого рангу ми маємо
![]()
Аналогічно, якщо -ф-
![]()
Теорема. Довільний тензор другого рангу завжди можна записати як суму двох тензорів: симетричного і антисиметричного.
Доведення цієї теореми
випливає з очевидної рівності
![]()
Тут додаток
![]() є
симетричним, а
є
симетричним, а![]() антисиметричним
виразом.
антисиметричним
виразом.
Цю теорему легко узагальнити на довільну пару індексів тензора будь якого рангу.
Спростимо нашу термінологію.
Коли задані коваріантні складові вектора
ми будемо говорити, що заданий коваріантний
вектор
![]() Аналогічно,
коли йдеться про контрваріантний вектор
ми маємо на увазі контрваріантні складові
цього вектора. Взагалі, мова йтиме про
коваріантний тензор
Аналогічно,
коли йдеться про контрваріантний вектор
ми маємо на увазі контрваріантні складові
цього вектора. Взагалі, мова йтиме про
коваріантний тензор![]() ,контрваріантний
тензор
,контрваріантний
тензор![]() ,
мішаний тензор
,
мішаний тензор![]() .
При цьому матимемо на увазі відповідно
коваріантні, контрваріантні і мішані
складові тензораТ.
.
При цьому матимемо на увазі відповідно
коваріантні, контрваріантні і мішані
складові тензораТ.
-80-
Приклади корисніші від правил.
І.Ньютон.
23. Приклади тензорів.
У фізиці і в математиці дійсно існують величини, що мають більш складну розмірність ніж скаляр і вектори. Іншими словами, ми наведемо приклади тензорів.
У першу чергу нам треба
показати, що попередньо введені величини
![]() /і
відповідно –
/і
відповідно –![]() /
є компонентами тензора.
/
є компонентами тензора.
Згадаємо, що
![]()
а при переході до нової системи
![]()
![]()
Тоді
![]()
- величини
![]() мають
такі такі ж трансформаційні властивості
як і коваріантні складові тензора
другого рангу. Отже,
мають
такі такі ж трансформаційні властивості
як і коваріантні складові тензора
другого рангу. Отже,![]() є коваріантним симетричним тензором.
є коваріантним симетричним тензором.
Аналогічно доводять, що
![]() є
контрваріантним тензором.
є
контрваріантним тензором.
Згадаємо тепер співвідношення /18.9/
![]()
І відзначимо, що операція
![]() є
операцією опускання верхнього індексу.
Тому
є
операцією опускання верхнього індексу.
Тому
![]()
Де
![]() є
мішаними компонентами метричного
цензора і
є
мішаними компонентами метричного
цензора і
![]() /23.1/
/23.1/
Згідно з загальним законом перетворення мішаних компонент тензора другого рангу ми маємо
![]()
Отже,
![]()
- символ Кронекера є мішаним тензором другого рангу а його компоненти мають однакові
-ф-
значення
-81-
в усіх координатних системах.
Далі два приклади тензорів ми проведемо, обмежуючись декартовими координатними системами.
Приклад 1. Тензор інерції твердого тіла.
Розглянемо рух твердого
тіла, що обертається з кутовою швидкістю
![]() навколо
нерухомої точки0.
Приймемо точку
0 за початок координат
і підрахуємо момент кількості руху тіла
відносно точки 0.
навколо
нерухомої точки0.
Приймемо точку
0 за початок координат
і підрахуємо момент кількості руху тіла
відносно точки 0.
Розглянемо елемент об’єму
![]() ,
,
що рухається з лінійною
швидкістю
![]() ,
,
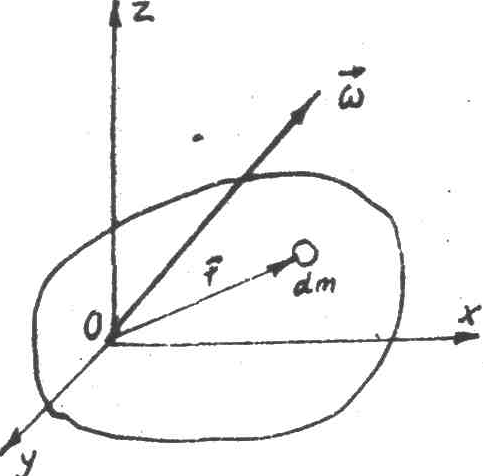 тоді
тоді
![]()
а момент кількості руху цього елемента
буде
рис.65 ![]() /23.2/
/23.2/
Момент кількості руху всього тіла
Знайдемо підсумовуючи /23.2/ по всьому об’єму тіла.
![]()
де
![]() густина
речовини. Використавши формулу
густина
речовини. Використавши формулу
![]()
ми одержимо
![]()
Проекції вектора –ф- на координатні осі дорівнюють
-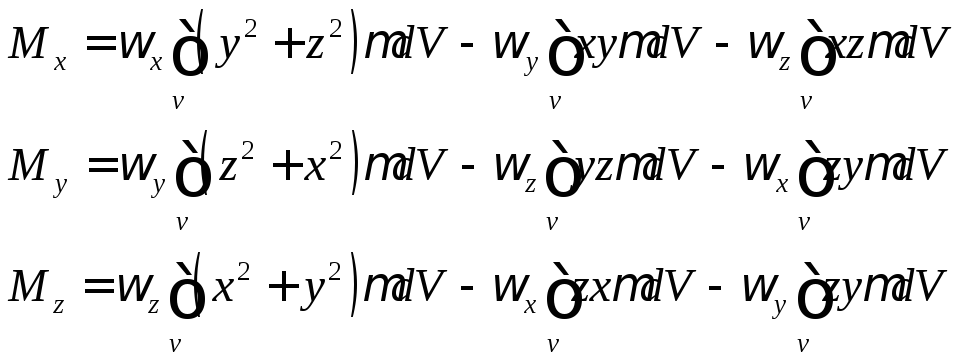 -
-
Введемо позначення
![]()
тоді
-84-
![]() є
скалярним добутком векторів
є
скалярним добутком векторів
![]() інваріантом,
тобто тензором рангу нуль. Таким чином
прирівнюючи два індекси /верхній і
нижній/ у виразі
інваріантом,
тобто тензором рангу нуль. Таким чином
прирівнюючи два індекси /верхній і
нижній/ у виразі![]() і
підсумовуючи по цьому індексу, ми
понизимо ранг тензора на дві одиниці.
Таку операцію називають згорткою.
і
підсумовуючи по цьому індексу, ми
понизимо ранг тензора на дві одиниці.
Таку операцію називають згорткою.
Операцію згортання двох індексі можна здійснити для довільного тензора рангу N, понижуючи при цьому його ранг на дві одиниці.
Нехай даний тензор з N1
коваріантними і N2
контрваріантними
індексами
![]()
Запишемо його закон перетворення при переході до нової системи
![]()
І розглянемо суму
![]()
- вираз, що має N1-1 коваріантних і N2-1 контрваріантних рухомих індексів. Тоді
![]()
Враховуючи, що вираз у дужці
є символом Кронекера
![]() одержуємо
одержуємо
![]()
Тобто
![]()
Ми одержали закон перетворення тензора рангу
![]()
Підкреслюємо, що операція згортання за двома контрваріантними індексами не приводить до тензора нижчого рангу. Легко переконатись, що вирази
![]()
![]()
Не мають тензорної розмірності.
Цілком зрозуміло, що згортання по різних парах індексів, взагалі кажучи, дає рівні рель тати. Наприклад,
![]()
-85-
/знак рівності можна поставити
тільки у випадку, коли тензор
![]() симетричний
стосовно до пари індексів
симетричний
стосовно до пари індексів![]() і
і![]() -/.
-/.
Тензори четвертого і вищих рангів можна згортати по двох парах індексів
![]() /24.2/
/24.2/
У результаті одержується тензор, ранг якого на чотири одиниці нижчий. В цьому легко переконатися, вивчаючи трансформаційні властивості виразу /24.2/.
Цікаво відзначити, що подвіцна
згортка добутку симетричного і
антисиметричного тензорів дорівнює
нулеві. Нехай
![]() симетричний,
симетричний,![]() -
антисиметричний тензор другого рангу:
-
антисиметричний тензор другого рангу:
![]()
Тоді 
Повернемось ще до згортки тензора другого рангу
![]()
Цей вираз є інваріантом –
сумою діагональних елементів матриці
тензора
![]() .
Його називають слідом матриціТ.
.
Його називають слідом матриціТ.
Коли задачу розв’язує інший , все ясно,
коли розв’язуєш сам, нічого не виходить.
Л.Ейлер
25. Деякі властивості симетричних тензорів другого рангу.
Будь-який тензор другого рангу можна записати на як суму двох тензорів – симетричного і антисиметричного. Тому доцільно вивчити окремо властивості симетричних і окремо властивості антисиметричних тензорів. Для простоти обмежимись розглядом цих тензорів у прямокутних системах координат.
Нехай Тік симетричний
Тік = Ткі
І будемо розглядати випадок, коли його складові Тіі дотатні.
Виберемо координатну систему xyz і розглянемо вираз
-86-
![]()
Він є згорткою двох тензорів:
Тік
і мішаного добутку
![]() Тому /25.1/ є інваріантом.
Тому /25.1/ є інваріантом.
Розглянемо рівняння
![]() /25.2/
/25.2/
у розгорнутому вигляді воно має вигляд
![]()
/25.2/
і є рівнянням поверхні другого порядку в системі xyz.
Щоб з’ясувати, з якою поверхнею ми маємо справу, знайдемо точки перетину цієї поверхні з координатними осями. Приймаючи y=z=0 знайдемо точки перетину поверхні з віссю х
![]()
![]()
- з віссю х поверхня перетинається в двох скінченних симетрично розміщених точках. Аналогічно, приймаючи х=z=0 . а також х=у=0
Знайдемо
![]()
![]()
- з осями у
і z
поверхня перетинається в двох скінченних,
симетрично розміщених точках.Щоб
остаточно з’ясувати з якоюповерхнею
ми маємо справу, знайдемо точки перетину
поверхні /25.2/ з довільною прямою
![]() -,
яка проходить через початок координат.
Приймемо
-,
яка проходить через початок координат.
Приймемо![]() за
вісь
за
вісь![]() нової
системи координат і врахуємо, що
нової
системи координат і врахуємо, що
![]()
Якщо
![]() ,
тоді
,
тоді
![]()
точками перетину є знову дві скінченні, симетрично розміщені точки.
Поверхня /25.2/ з еліпсоїдом, однак, у загальному випадку його осі не збігаються з координатними осями х, у, z.
Виберемо ще одну координатну систему х, у, z, осі якої збіга-
-87-
ються з напрямками осей еліпсоїда. У цій системі
![]() де
де![]() ,
- довжина півосей еліпсоїда.
,
- довжина півосей еліпсоїда.
З другого боку
![]() але
також
але
також
![]()
Останні дві рівності збігаються тільки тоді, коли
![]()
![]()
Таким чином, системі х, у, z матриця симетричного тензора набуває вигляду
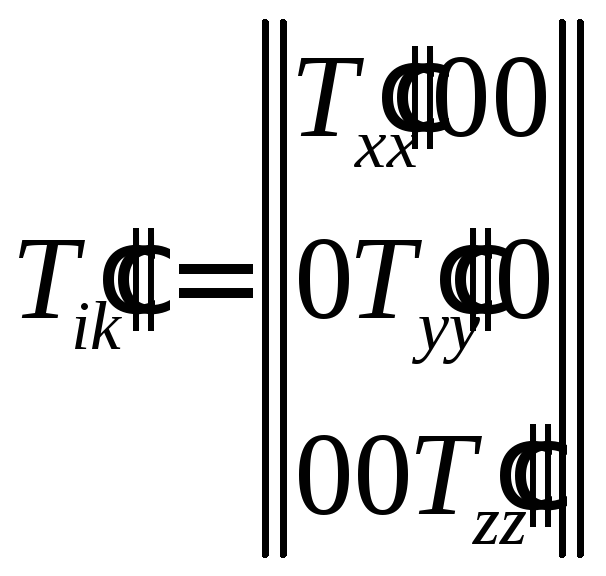
- недіагональні складові тензора перетворюються в нуль. Приходимо до висновку, що для будь якого симетричного тензора можна знайти таку систему координат, в якій відмінними від нуля є тільки три складові тензора.
Еліпсоїд, визначений за рівнянням /25.2/ називають еліпсоїдом тензора.
Розглянемо, наприклад, тензор
інерції
![]() .
Як згадувалось раніше, недіагональні
складові цього тензора характеризують
вплив осі обертання на тіло, тобто, при
.
Як згадувалось раніше, недіагональні
складові цього тензора характеризують
вплив осі обертання на тіло, тобто, при![]()
![]() тіло зазнає шкідливих впливів з боку
осі обертання, воно деформується. Щоб
уникнути таких шкідливих впливів треба,
щоб обертання відбувалося навколо
однієї з головних осей інерції, тобто
однієї з осей еліпсоїда інерції.
тіло зазнає шкідливих впливів з боку
осі обертання, воно деформується. Щоб
уникнути таких шкідливих впливів треба,
щоб обертання відбувалося навколо
однієї з головних осей інерції, тобто
однієї з осей еліпсоїда інерції.
6 + 3 = 9
/з підручника вищої математики
для футбольних тренерів/
