26. Антисиметричні тензори другого рангу.

Нагадаємо, що тензор другого рангу називаємо асиметричним, якщо

-88-

/26.1/

З /26.1/ випливає, що

І матриця тензора набуває вигляду

/26.2/

- антисиметричний тензор другого рангу має три різні, відмінні від нуля компоненти.

Введемо позначення

І переконаємось, що є компонентами псевдовектора. Для цього запишемо закон перетворення тензора

Тоді

/26.3/

-89-

Вирази для знайдемо, використовуючи правило циклічної перестановки

/26.4/

/26.5/

У випадку перетворення інверсії

І тоді

/26.6/

- величини дійсно перетворюються як складові псевдовектора.

Як тільки розв’язана одна проблема,

на її місце випливають нові проблеми.

Д.Гільберт

27. Диференціальні операції над тензорами.

Розглянемо тензорне поле – випадок, коли компоненти тензора є функціями координат точки

/26.1/у

Прикладами тензорних полів є:

скалярне поле

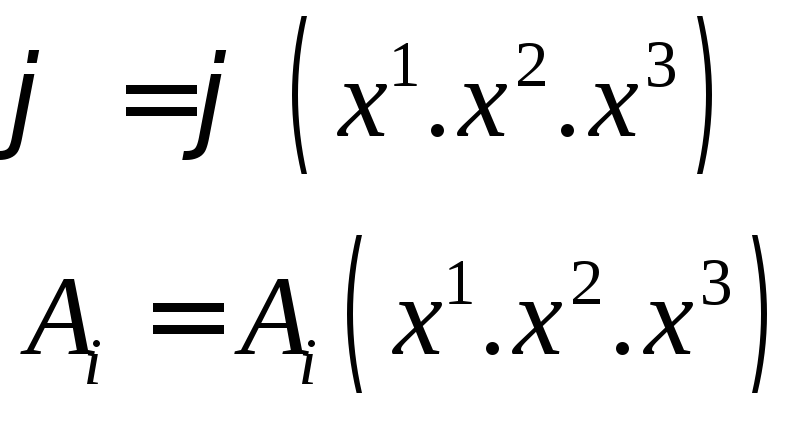
векторне поле

тензорне поле напружень у деформованому середовищі

/кожній точці деформованого середовища відповідають свої значення складових тензора напружень/.

Розглянемо скалярне поле і знайдемо три часткові похідні по координатах.

-90-

Як відомо, вони визначають коваріантний вектор градієнта скалярної функції. Таким чином, шляхом звичайного диференціювання ми можемо з тензора рангу одержати тензор рангу

Розглянемо тепер коваріантний вектор – функцію точки

і утворимо часткові похідні

Переконаємось, що дев ять величин /ми будемо називати їх мішаними похідними/ визначають коваріантний тензор другого рангу. При переході до нової системи

Отже, є коваріантним тензором.

Подібним чином можна переконатися що дев ять величин

є компонентами мішаного тензора другого рангу. Це з рештою, випливає і з того, що мішані похідні /27.2/ і /27.3/ є мішаними добутками вектора і вектора/

Таким чином, шляхом мішаного диференціювання ми підвищуємо ранг тензора на одиницю – тензора рангу одержуємо тензор рангу.

Згортаючи тензор /27.3/ ми одержимо тензор рангу - відомий вираз для дивергенції тензора

Різниця мішаних похідних

/27.3/

є антисиметричним тензором другого рангу , який, по суті, є ротором вектора.

Можна переконатися, що шляхом мішаного диференціювання можна підвищити на одиницю ранг довільного тензора. Часткові похідні від тензора рангу

/27.4/

-91-

є компонентами тензора рангу . Для цього треба вивчити трансформаційні властивості величин /27.5/. Зокрема, похіднівизначають коваріантний тензор третього рангу.

Згорнемо тензор по індексахі. Очевидно,резуль – вектор, позначимо його через .Тоді

/27.5/

або в проекціях на координатні осі

/27.5/

Кожний з цих виразів нагадує вираз для дивергенції вектора /сума часткових похідних по координатах/, тому вектор –a називають векторною дивергенцією тензора. Рівність /27.6/ символічно можна записати

/27.5/

Векторна дивергенція тензора часто зустрічається в теоретичній фізиці /механіка деформованого середовища, електродинаміка, теорія відносності/.

Операції згортання і операції мішаного диференціювання є, в певному сенсі, протилежними. Перша понижує ранг тензора на дві одиниці, друга – підвищує ранг на одиницю. Це дає змогу побудувати тензор будь-якого рангу, якщо заданий тензор рангу .

Наприклад, застосовуючи операцію мішаного диференціювання, а потім згортання

Як завжди, розв’язування однієї задачі породжує

нові. І останньої задачі ніколи не буде.

А.Смородинський