
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
.doc
т.е. дисперсия есть
математическое ожидание квадрата
центрированной случайной величины.
Пользуются символами
![]() .
.
Опираясь на формулы для дисперсии, можно доказать такие свойства дисперсии.
1с)
![]()
![]() .
.
2с)
![]()
![]() .
.
3с)
![]()
![]() .
.
Величину
![]() называют корреляционным моментом
случайных величин
называют корреляционным моментом
случайных величин
![]() и
и
![]() .
.
Для вычисления
![]() по опытным данным используют формулу
по опытным данным используют формулу
![]() .
.
Пары
![]() наблюдались в
наблюдались в
![]() опытах.
опытах.
Если
![]() ,
то случайные величины
,
то случайные величины
![]() и
и
![]() называют некоррелированными.
называют некоррелированными.
5) Моменты случайной величины
Сам термин и способ построения заимствовал из механики (статические, центробежные моменты, моменты инерции).
Начальным
моментом порядка
![]() называется число
называется число
![]() .
.
Очевидно
![]() .
.
Центральным
моментом порядка
![]() называется число
называется число
![]() .
.
![]() ,
,
![]() .
.
Центральные моменты выражаются через начальные.
![]()
![]() .
.
Мы получили часто используемую формулу, связывающую дисперсию, начальный момент 2го порядка и математическое ожидание.
![]()
 .
.
![]() – для дискретных
случайных величин.
– для дискретных
случайных величин.
![]() – для непрерывных
случайных величин.
– для непрерывных
случайных величин.
Чем больше моментов мы рассматриваем, тем подробнее информация о случайной величине. Однако, надежно вычислить по опытным данным моменты высоких порядков бывает затруднительно. Поэтому в практических задачах моменты выше четвертого порядка не рассматриваются.
Важным является центральный момент 3го порядка.
![]() ,
,
![]() .
.
О н
характеризует асимметрию плотности
вероятности.
н
характеризует асимметрию плотности
вероятности.


Но величина
![]() размерная и поэтому «чувствительна к
изменению масштаба» (в том числе и к
рассеиванию).
размерная и поэтому «чувствительна к
изменению масштаба» (в том числе и к
рассеиванию).
Поэтому вводят безразмерную величину коэффициент асимметрии
![]() .
.
Точно также вместо
![]() вводят величину, называемую эксцессом
вводят величину, называемую эксцессом
![]() .
.
Эксцесс характеризует остроконечность распределения по отношению к нормальному закону.

Пример 1. Найти
дисперсию случайной величины
![]() ,
если дан ряд распределения.
,
если дан ряд распределения.
-

1
2
5

0,3
0,5
0,2
Решение. 1) Найдем математическое ожидание:
![]() .
.
2) Найдем все возможные значения квадрата отклонения:
![]() ,
,
![]() ,
,
![]() .
.
-
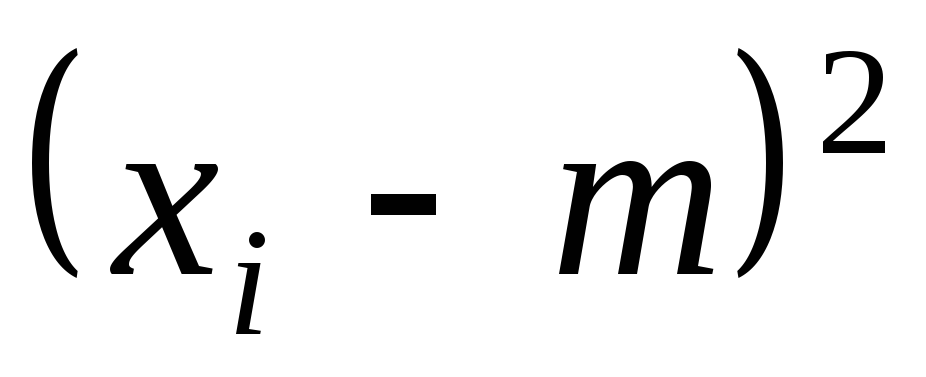
1,69
0,09
7,29

0,3
0,5
0,2
![]()
![]() .
.
Другой способ
![]() ,
,
![]() .
.
-

1
4
25

0,3
0,5
0,2
![]() ,
,
![]() ,
,
![]()
![]() .
.
Пример 2.
Найти математическое ожидание и дисперсию
случайной величины
![]() ,
заданной функцией распределения
,
заданной функцией распределения


Математическое
ожидание.
![]() ,
возможные значения случайных величин
лежат от
,
возможные значения случайных величин
лежат от
![]() до
до
![]() по
по
![]() только на
только на
![]() ,
вне этого интервала = 0.
,
вне этого интервала = 0.
![]() .
.
Дисперсия
![]()
![]() .
.
Повторение испытаний. Формула Бернулли
Пусть производится
![]() независимых опытов, в каждом из которых
событие
независимых опытов, в каждом из которых
событие
![]() может появляться с одной и той же
вероятностью –
может появляться с одной и той же
вероятностью –
![]() .
.
Такая схема
испытаний называется «схемой испытаний
Бернулли». Требуется вычислить
вероятность
![]() того, что в указанной серии опытов
событие появится ровно
того, что в указанной серии опытов
событие появится ровно
![]() раз. Ясно, что
раз. Ясно, что
![]() .
Еще говорят, что
.
Еще говорят, что
![]() – вероятность
– вероятность
![]() успехов при
успехов при
![]() испытаниях.
испытаниях.
Пример.
Производится 3 выстрела по мишени.
Вероятность попадания при каждом
выстреле равна
![]() .
Какова вероятность поражения цели ровно
двумя выстрелами?
.
Какова вероятность поражения цели ровно
двумя выстрелами?
Решение. Пусть
![]() – попадание при
– попадание при
![]() -ом
выстреле.
-ом
выстреле.
![]() – событие 2 успеха при 3х
выстрелах.
– событие 2 успеха при 3х
выстрелах.
![]() ?
?
![]() ,
,
где
![]() .
.
Обобщим на
![]() успехов в
успехов в
![]() опытах и получим следующую формулу
вероятности
опытах и получим следующую формулу
вероятности
![]() успехов в
успехов в
![]() опытах по схеме Бернулли.
опытах по схеме Бернулли.

![]() Это
и есть формула Бернулли.
Это
и есть формула Бернулли.
Биномиальное распределение
Говорят, что случайная величина, выражающая число успехов в схеме испытаний Бернулли имеет биномиальное распределение
![]() .
.
Для биномиального распределения можно вывести числовые характеристики.
![]() целое
число от
целое
число от
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Продолжим
рассмотрение предыдущего примера и
получим ряд распределения для
![]() ,
а также числовые характеристики.
,
а также числовые характеристики.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
-

0
1
2
3

0,064
0,288
0,432
0,216

Числовые характеристики
![]() – это значит
случайная
– это значит
случайная
величина соответствует наибольшей вероятности;
![]() – среднее число
успехов;
– среднее число
успехов;
![]() ;
;
![]() .
.
Число
![]() ,
которому при заданном
,
которому при заданном
![]() соответствует максимальная биномиальная
вероятность
соответствует максимальная биномиальная
вероятность
![]() называется наивероятнейшим числом
появления события
называется наивероятнейшим числом
появления события
![]() .
При заданных
.
При заданных
![]() и
и
![]() это число определяется неравенствами
это число определяется неравенствами
![]() .
.
Если число
![]() не является целым, то
не является целым, то
![]() равно целой части этого числа
равно целой части этого числа
![]() .
.
Если же
![]() – целое число, то
– целое число, то
![]() имеет два значения
имеет два значения
![]() и
и
![]() .
.
Пример. Доля изделий высшего сорта на данном предприятии составляет 30%. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий.
Решение. По условию
![]() ,
,
![]() ,
,
![]() .
Составляем двойное неравенство:
.
Составляем двойное неравенство:
![]()
![]() ,
,
![]() 22.
22.
Замечания:
1. Если требуется
вычислить вероятность того, что число
успехов
![]() при
при
![]() испытаниях заключено между натуральными
числами
испытаниях заключено между натуральными
числами
![]() и
и
![]() ,
то, воспользовавшись независимостью
испытаний и теоремой сложения вероятностей,
получим следующую формулу
,
то, воспользовавшись независимостью
испытаний и теоремой сложения вероятностей,
получим следующую формулу
 .
.
2. Вероятность
получения хотя бы одного успеха при
![]() испытаниях можно найти, используя
противоположное событие:
испытаниях можно найти, используя
противоположное событие:
![]() .
.
Пример. Симметричную монету бросают шесть раз. Определить вероятность выпадения цифры:
а) ровно 4 раза
![]() .
.
б) не более 3х раз

![]() .
.
в) хотя бы один раз
![]() .
.
Когда число
независимых испытаний
![]() велико, вычисление
велико, вычисление
![]() по формуле Бернулли затруднительно,
т.к. требует вычисления факториалов
больших чисел. В дальнейшем мы получим
асимптотические формулы, используемые
при больших
по формуле Бернулли затруднительно,
т.к. требует вычисления факториалов
больших чисел. В дальнейшем мы получим
асимптотические формулы, используемые
при больших
![]() .
.
Распределение Пуассона
Пусть в схеме испытаний Бернулли
1)
![]() ;
;
2)
![]() ;
;
3)
![]() (можно
(можно
![]() ).
).
Что произойдет с биномиальным распределением?

 .
.
![]()
 – распределение Пуассона.
– распределение Пуассона.
Это распределение однопараметрическое (параметр а).
Числовые характеристики распределения Пуассона найдем тоже предельным переходом.
![]()
![]()
![]()
То, что
![]() ,
можно использовать как подтверждение
пуассоновского распределения.
,
можно использовать как подтверждение
пуассоновского распределения.
Если по опытным данным
![]() ,
,
то это будет свидетельствовать в пользу гипотезы о пуассоновском распределении.
Как следует из предыдущего, при определенных условиях
![]() .
.
Это выполняется,
когда
![]() порядка нескольких сотен, а
порядка нескольких сотен, а
![]() .
Иногда закон Пуассона называют законом
редких явлений.
.
Иногда закон Пуассона называют законом
редких явлений.
Распределение Пуассона является точным в следующей задаче:
Пусть на оси х случайным образом размещены точки с выполнением следующих условий.
1) Вероятность
попадания любого заданного числа точек
на отрезок длиной
![]() зависит лишь от
зависит лишь от
![]() и не зависит от положения отрезка на
оси х – однородность.
и не зависит от положения отрезка на
оси х – однородность.
2) Точки расположены так, что вероятность иметь любое заданное число точек на каком-либо отрезке не зависит от того, сколько точек попало на любой другой отрезок, не пересекающийся с первым – независимость.
3) Точки расположены по одной – ординарность.
Пусть требуется
определить вероятность того, что отрезок
длиной
![]() содержит ровно
содержит ровно
![]() точек. Количество точек здесь распределено
по закону Пуассона. Если
точек. Количество точек здесь распределено
по закону Пуассона. Если
![]() – средняя плотность точек, то
– средняя плотность точек, то
![]() и искомая вероятность
и искомая вероятность
![]() .
.
Если рассматривать события, происходящие во времени, то тогда мы имеем поток событий, т.е. последовательность событий, наступающих в случайные моменты времени.
Примеры:
-
поступление вызовов на АТС;
-
прибытие клиентов в мастерскую бытового обслуживания;
-
последовательность отказов элементов в приборе.
Тогда вышеприведенные условия получают другие названия.
1) однородность
![]() стационарность;
стационарность;
2) независимость
![]() отсутствие последствия;
отсутствие последствия;
3) ординарность
![]() ординарность.
ординарность.
Такой поток называют простейшими (пуассоновскими).
Число
![]() называют интенсивностью потока –
это среднее число событий появляющихся
в единицу времени.
называют интенсивностью потока –
это среднее число событий появляющихся
в единицу времени.
Формулу Пуассона можно считать математической моделью простейшего потока событий.
![]()
Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно 2м. Найти вероятность того, что за пять минут поступит 2 вызова.
Решение.
![]() ,
,
![]() выз.,
выз.,
![]() мин.
мин.
![]() .
.
Событие практически невозможное.
Равномерное распределение
Это распределение, плотность вероятности которого определяется так:


Величину этой
![]() можно найти из таких соображений.
можно найти из таких соображений.
Площадь прямоугольника
равна 1, основание его –
![]() ,
значит
,
значит
![]() .
.

Его еще называют распределением с постоянной плотностью.
Найдем числовые характеристики.
![]() – нет (амодальное
распределение).
– нет (амодальное
распределение).
![]() .
.

![]() .
.
![]() ,
,
![]() ,
коэффициент асимметрии равен нулю, т.к.
распределение симметричное.
,
коэффициент асимметрии равен нулю, т.к.
распределение симметричное.
 .
.
![]() .
.
плосковершинность.
Вероятность
попадания в заданный интервал
![]() .
.
![]()
– соответствует геометрической вероятности.
Пример. Поезда данного маршрута трамвая идут с интервалом 5 мин. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее, чем через минуту после ухода предыдущего трамвая и не позже, чем за две минуты до отхода следующего?
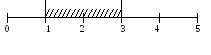
![]() .
.
Экспоненциальное распределение
Показательным
(экспоненциальным) называют распределение
вероятностей непрерывной случайной
величины
![]() ,
которое описывается плотностью
,
которое описывается плотностью

где
![]() – постоянная положительная величина.
– постоянная положительная величина.
Мы видим, что
экспоненциальное распределение
определяется одним параметром
![]() .
.

Найдем функцию распределения экспоненциального закона.
![]() .
.


Вычислим числовые характеристики экспоненциального распределения.


 .
.
![]() .
.
![]() .
.
![]() – это есть
математическое ожидание.
– это есть
математическое ожидание.
![]()
 .
.
![]() .
.
![]()
 .
.
