
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
.doc
Случайные величины и их распределения
Случайной величиной называют переменную величину, которая в зависимости от исходов испытания принимает значения, зависящие от случая.
Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной.
Случайная величина, которая может принимать все значения из некоторого промежутка, называется непрерывной случайной величиной.
Случайные величины
будем обозначать заглавными буквами
![]() …,
а их значения – строчными буквами
…,
а их значения – строчными буквами
![]() …
– их называют еще возможными значениями.
…
– их называют еще возможными значениями.
Тогда возможно рассмотрение событий
![]()
– случайная
величина Х приняла после опыта
значение
![]() .
.
![]()
– случайная
величина Х приняла после опыта
значение меньшее, чем
![]() .
.
Замечание. Всякое событие можно формально заменить случайной величиной, принимающей два значения: 0 – когда событие не появилось и 1 – когда появилось. Такой случайной величине можно сопоставить вероятности появления и непоявления события.
|
|
0 |
1 |
|
|
1 |
р |


Соотношение вида
![]()
связывает возможные значения случайной величины и их вероятности и называется законом распределения случайной величины.
Закон распределения может быть задан аналитически (в виде формулы), таблично и графически.
Если закон распределения задан таблично, то эту таблицу называют рядом распределения.
-
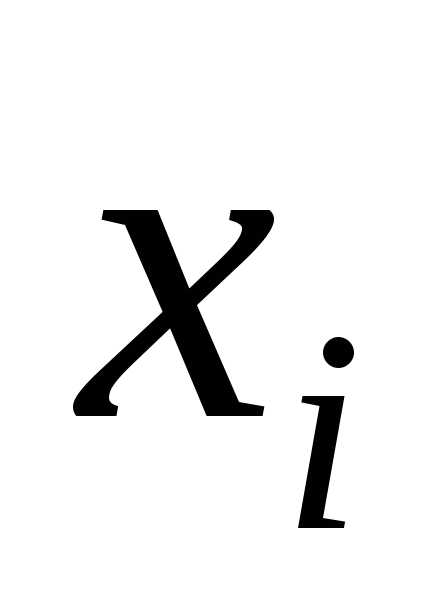

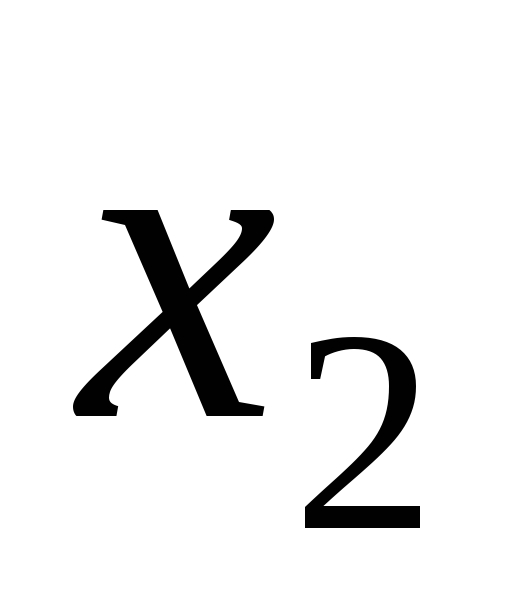
………………
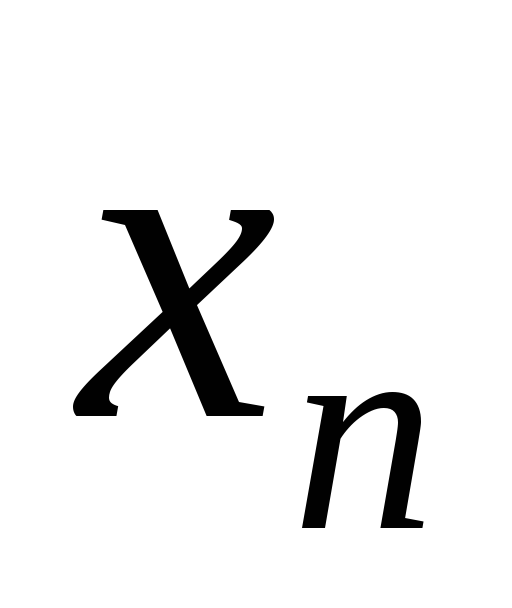
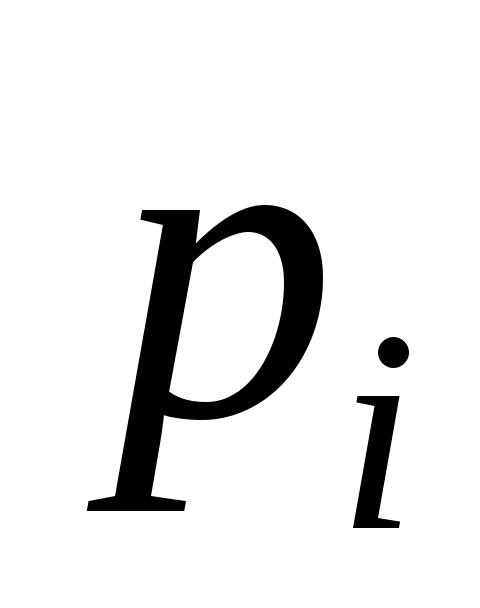
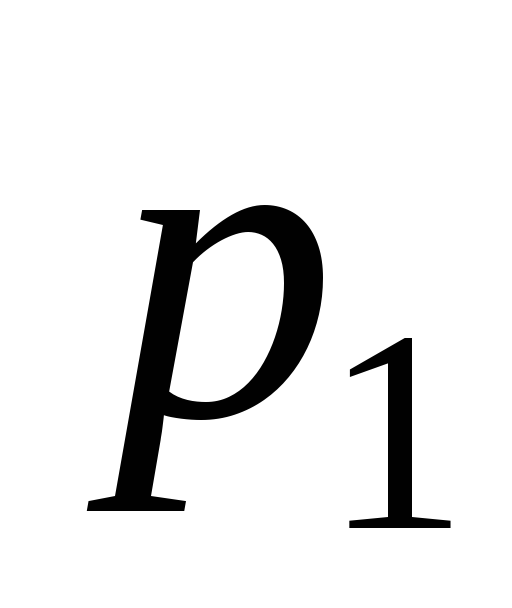

………………

Заметим, что
![]() ,
т.к. события
,
т.к. события
![]()
![]() образуют полную группу событий.
образуют полную группу событий.
Д ля
наглядности закон распределения
дискретной случайной величины изображают
графически, для чего строят точки
ля
наглядности закон распределения
дискретной случайной величины изображают
графически, для чего строят точки
![]() и соединяют их последовательными
отрезками прямых. Получающаяся при этом
ломаная линия называется многоугольником
распределения случайной величины
и соединяют их последовательными
отрезками прямых. Получающаяся при этом
ломаная линия называется многоугольником
распределения случайной величины
![]() .
.
Если дискретная
случайная величина
![]() принимает бесконечную последовательность
значений
принимает бесконечную последовательность
значений
![]() соответственно с вероятностями
соответственно с вероятностями
![]() ,
то ее закон распределения определяется
формулами
,
то ее закон распределения определяется
формулами
![]()
![]() ,
,
![]() .
.
Ряд распределения имеет вид
|
|
|
|
……………… |
|
……………… |
|
|
|
|
……………… |
|
……………… |
Заметим, что ряд,
составленный из чисел
![]() ,
сходится и его сумма равна единице.
,
сходится и его сумма равна единице.
Функция распределения
Для непрерывной случайной величины закон распределения нужно задавать по-другому, чем в случае дискретной случайной величины.
Рассмотрим наиболее общий подход к формулировке закона распределения и введем наиболее общую и универсальную характеристику случайных величин – функцию распределения, которая вводится соотношением
![]() .
.
Таким образом –
это вероятность того, что случайная
величина
![]() примет значение меньшее, чем
примет значение меньшее, чем
![]() .
.
Геометрически это
означает следующее:
![]() – вероятность того, что случайная
величина
– вероятность того, что случайная
величина
![]() примет значение, которое изображается
точкой на числовой прямой, расположенной
слева от точки
примет значение, которое изображается
точкой на числовой прямой, расположенной
слева от точки
![]() .
.

Теперь можно дать такое определение непрерывной случайной величины.
С
 лучайная
величина называется непрерывной, если
ее функция распределения
лучайная
величина называется непрерывной, если
ее функция распределения
![]() является непрерывно дифференцируемой.
является непрерывно дифференцируемой.
Функцию распределения
называют также интегральной функцией,
или интегральным законом распределения
случайной величины
![]() .
.
Если дана функция
распределения
![]() ,
то нетрудно вычислить и вероятность
попадания величины в интервал
,
то нетрудно вычислить и вероятность
попадания величины в интервал
![]() ,
т.е.
,
т.е.
![]() .
.
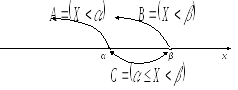
![]() ,
но
,
но
![]() .
.
Применима формула сложения вероятностей
![]() ,
,
но
![]() ,
,
![]() ,
,
![]() .
.
Значит,
![]() . (1)
. (1)
Отметим еще свойства функции распределения.
1с.
![]() неубывающая функция. Действительно,
это следует из (1), т.к.
неубывающая функция. Действительно,
это следует из (1), т.к.
![]() ,
то из
,
то из
![]() следует
следует
![]() .
.
2с. Если все
возможные значения случайной величины
![]() принадлежат интервалу
принадлежат интервалу
![]() ,
то для ее функции распределения
,
то для ее функции распределения
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Если же все возможные
значения случайной величины х
принадлежат бесконечному интервалу
![]() ,
то
,
то
![]() .
.
Эти свойства позволяют говорить о графике функции распределения – это график неубывающей функции, значения которой начинаются от нуля и
доходят до 1, причем в отдельных точках могут быть разрывы 1го ряда (скачки).


Функция распределения
![]() для дискретной случайной величины
для дискретной случайной величины
![]() ,
которая может принимать значения
,
которая может принимать значения
![]() с соответствующими вероятностями:
с соответствующими вероятностями:
![]() ,
имеет вид:
,
имеет вид:
![]()
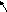 . (2)
. (2)
(это означает, что суммируются вероятности тех значений, которые меньше х.)
Пример. Закон распределения дискретной случайной величины задан следующей таблицей:
-

0
1
2
3

0,2
0,4
0,3
0,1
Найти функцию распределения случайной величины.
Решение. Для построения функции распределения воспользуемся формулой (2).
-
При
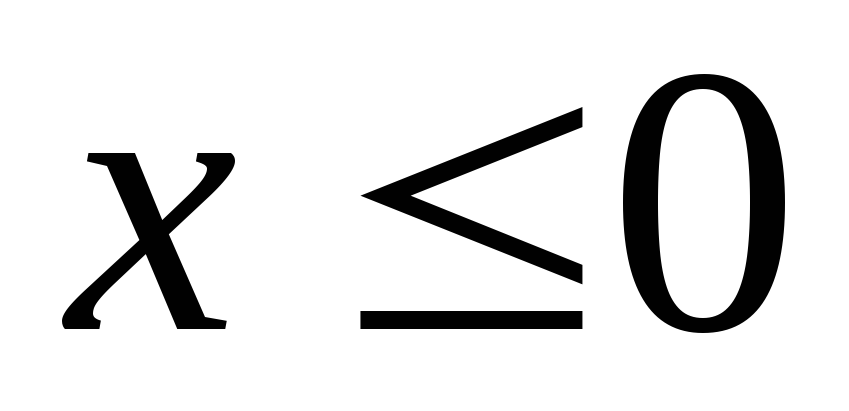
 .
. -
При

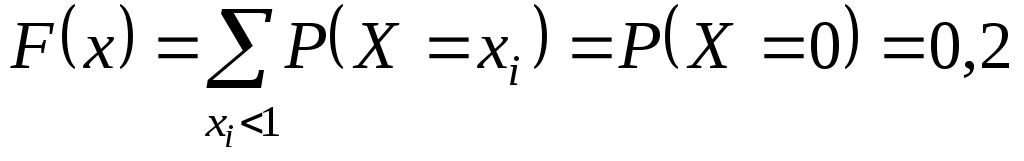 .
. -
П
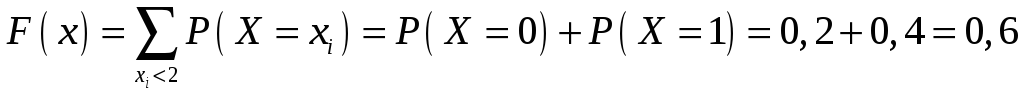 ри
ри
 .
.
-
При
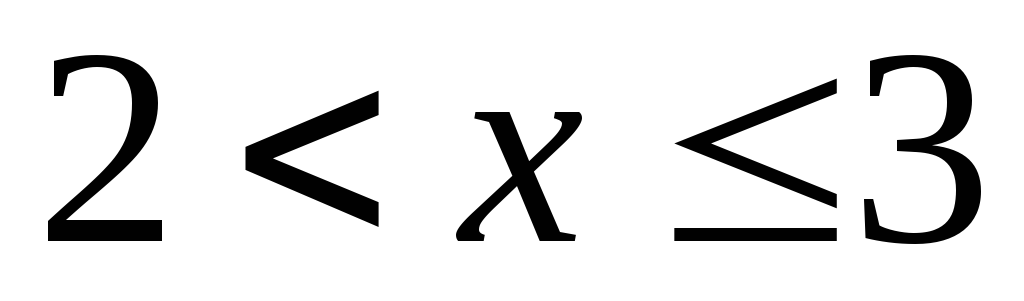
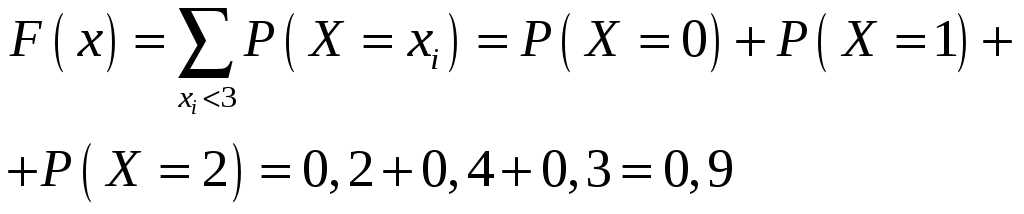
-
П
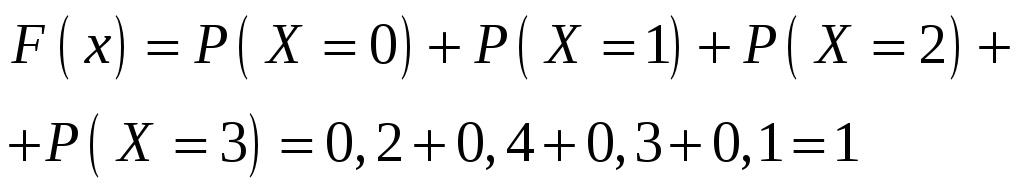 ри
ри

.

Будем неограниченно
уменьшать интервал
![]() ,
полагая
,
полагая
![]() .
В пределе, очевидно, получим вероятность
того, что величина примет одно заданное
определенное значение.
.
В пределе, очевидно, получим вероятность
того, что величина примет одно заданное
определенное значение.
![]() .
.
Если
![]() – непрерывна, то этот предел равен нулю,
т.е.
– непрерывна, то этот предел равен нулю,
т.е.
![]() .
Таким образом, вероятность любого
отдельного значения непрерывной
случайной величины равна нулю.
.
Таким образом, вероятность любого
отдельного значения непрерывной
случайной величины равна нулю.
Заметим, что
равенство нулю вероятности отдельно
взятого значения случайной величины
не означает, что эта величина не может
появиться. Из того, что
![]() следует только, что при неограниченном
повторении опыта данное событие должно
появиться однократно, или крайне редко.
следует только, что при неограниченном
повторении опыта данное событие должно
появиться однократно, или крайне редко.
Например, изготовление эталонов.
Исходя из сказанного выше, должны выполняться равенства:
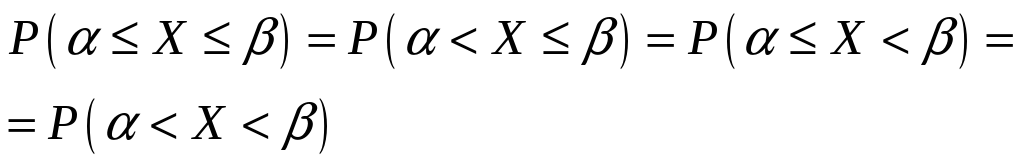
и
![]() .
.
Плотность вероятности
Плотностью
распределения (или дифференциальной
функцией распределения) случайной
величины
![]() в точке
в точке
![]() называется предел отношения вероятности
попадания значений этой величины в
интервал
называется предел отношения вероятности
попадания значений этой величины в
интервал
![]() к длине
к длине
![]() отрезка
отрезка
![]() ,
когда последняя стремится к нулю.
,
когда последняя стремится к нулю.
![]() . (1)
. (1)
Нетрудно показать, что
![]() . (2)
. (2)
Действительно:
![]() .
.
Кривая, изображающая плотность вероятности, называется кривой разрешения.
Пользуясь теоремами интегрального исчисления, можно записать
![]() .
.
Тогда вероятность
попадания значений случайной величины
![]() в интервал
в интервал
![]() равна
равна
![]() .
.
Плотность распределения обладает следующими свойствами:
1с)
![]() неотрицательная функция, т.к.
неотрицательная функция, т.к.
![]() неубывающая, а
неубывающая, а
![]() .
.
2с)
![]() – нормированность.
– нормированность.
Числовые характеристики случайных величин
1) Мода случайной величины
Мода дискретной случайной величины – ее значение, отвечающее наибольшей вероятности.
![]() .
.

![]() .
.
Мода непрерывной случайной величины – ее значение, отвечающее максимальному значению плотности вероятности.

Унимодальное
![]() .
.
Р аспределения
могут быть:
аспределения
могут быть:
-
полимодальные
( бимодальное)
бимодальное)
-
а
 нтимодальные
нтимодальные -
(амодальное)
2) Медиана и квартили случайных величин
Будем рассматривать непрерывные случайные величины. Квантилем порядка р называется корень уравнения
![]() ,
,
где
![]() – функция распределения.
– функция распределения.

При
![]() получаем медиану. Обозначается
получаем медиану. Обозначается
![]() .
.
![]() .
.
Таким образом, это
значение случайной величины такое, что
вероятность того, что случайная величина
примет значение больше или меньше
![]() ,
одинакова.
,
одинакова.

3) Математическое ожидание случайной величины
Рассмотрим
дискретную случайную величину. Пусть
произведено
![]() опытов, в которых
опытов, в которых
![]() наблюдалось
наблюдалось
![]() раз. Тогда статическое среднее (среднее
арифметическое по всем наблюдениям)
вычисляется по формуле
раз. Тогда статическое среднее (среднее
арифметическое по всем наблюдениям)
вычисляется по формуле
![]() .
.
При
![]()
![]() приближается к
приближается к
![]() ,
тогда
,
тогда
![]() приближается к величине
приближается к величине
![]()
 ,
,
которая называется математическим ожиданием дискретной случайной величины.
Математическое ожидание называют еще центром рассеивания случайной величины.
Другие обозначения:
![]() ,
,
![]() .
.
Таким образом, при
увеличении числа опытов среднее
арифметическое значение случайной
величины
![]() будет приближаться к математическому
ожиданию.
будет приближаться к математическому
ожиданию.
Эта связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел. Все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Сейчас речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно, при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается к постоянной величине – математическому ожиданию.
Например, многократное взвешивание с вычислением среднего арифметического.
При формальном (аксиоматическом) построении теории вероятностей доказываются следующие теоремы, выражающие закон больших чисел.
а) Теорема Чебышева
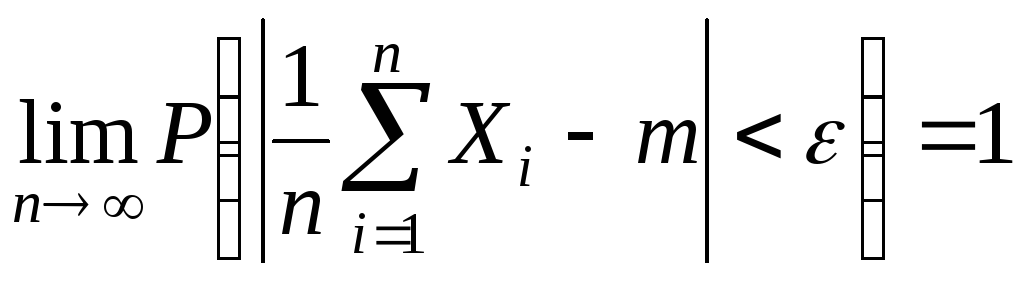
![]() .
.
б) Теорема Бернулли
![]()
![]() ,
,
где
![]() – случайная величина, отвечающая
наблюдению
– случайная величина, отвечающая
наблюдению
![]() в i-ом опыте,
в i-ом опыте,
т – математическое ожидание случайной величины.
Для непрерывной случайной величины математическое ожидание вводится путем предельного перехода.
Пусть дана
непрерывная случайная величина
![]() ,
введем аппроксимирующую ее дискретную
случайную величину
,
введем аппроксимирующую ее дискретную
случайную величину
![]() со значениями
со значениями
![]() ,
которым отвечают вероятности.
,
которым отвечают вероятности.
![]() ,
,
где
![]() – плотность распределения.
– плотность распределения.
Тогда
![]() .
.
Переходим к пределу
при
![]() .
При этом функция распределения дискретной
случайной величины
.
При этом функция распределения дискретной
случайной величины
![]() сходится к функции распределения
непрерывной случайной величины
сходится к функции распределения
непрерывной случайной величины
![]() .
.
![]() ,
,
![]() –
–
математическое
ожидание непрерывной случайной величины
![]() .
.
Опираясь на формулы для математического ожидания нетрудно показать справедливость следующих свойств.
1с)
![]() ;
;
2с)
![]() ;
;
3с)
![]() ;
;
4с)
![]() ,
,
Х и Y – независимые случайные величины.
4) Дисперсия и среднее квадратическое отклонение случайной величины
Мода, медиана, математическое ожидание характеризуют положение случайной величины, но не характеризуют рассеивание.

Для характеристики рассеивания нужно рассматривать отклонение
![]() .
.
Пусть имеем
![]() опытов для дискретной случайной величины,
причем
опытов для дискретной случайной величины,
причем
![]() появилось
появилось
![]() раз. Рассмотрим среднее квадратическое
значение для отклонений от центра
рассеивания.
раз. Рассмотрим среднее квадратическое
значение для отклонений от центра
рассеивания.
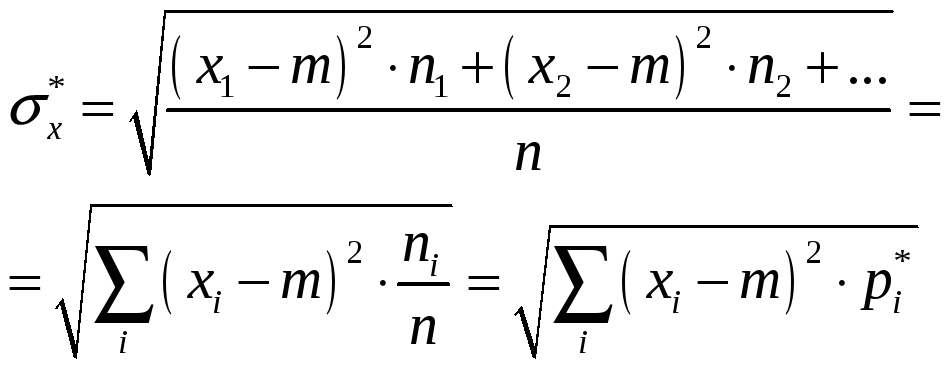 ,
,
при
![]()
![]() и тогда
и тогда
![]() .
.
![]()
– среднее
квадратическое отклонение случайной
величины
![]() .
.
Величина
![]() – дисперсия
случайной величины
– дисперсия
случайной величины
![]() .
.
![]()
– связь между средним квадратическим отклонением и дисперсией.
Для непрерывной случайной величины по аналогии с математическим ожиданием имеем
![]() .
.
Проанализировав
формулы для дисперсии мы можем
рассматривать ее как математическое
ожидание случайной величины
![]()
![]() .
.
Вводится понятие центрированной случайной величины
![]() ,
,
и тогда
![]() ,
,
