СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Таким образом, для экспоненциального распределения – это может служить критерием для установления по экспериментальным данным экспоненциального закона.

,

и т.д.

.

Найдем коэффициент асимметрии.

,

,

– асимметрия с крутой левой стороны.

Эксцесс

– островершинность.

Формула надежности

Будем называть элементом некоторое устройство независимо от того, «простое» оно или «сложное». Пусть элемент начинает работать момент времени , а по истечении времени длительностью происходит отказ. Обозначим через непрерывную случайную величину – длительность времени безотказной работы элемента.

Если элемент проработал безотказно (до наступления отказа) время, меньшее , то следовательно, за время длительностью наступит отказ. Таким образом, функция распределения определяет вероятность отказа за время длительностью . Следовательно, вероятность безотказной работы за это же время длительностью , есть вероятность противоположного события .

Это и есть функция надежности, она определяет вероятность безотказной работы элемента за время длительностью .

При мгновенных отказах функция распределения принимает экспоненциальный закон

.

– это и есть экспоненциальный закон надежности.

позволяет найти вероятность безотказной работы элемента на интервале времени длительностью .

Величина – интенсивность отказов, т.е. число отказов в единицу времени.

Пример. Время безотказной работы элемента распределено по показательному закону

при .

Найти вероятность того, что элемент проработает безотказно 100 часов.

Решение. По условию интенсивность отказов .

.

Значит, приближенно вероятность равна 0,14.

Заметим, что мы брали интенсивность отказов постоянной. На самом деле

.

В этом случае надежность нужно рассчитывать так.

.

(Модель отказа)

Характеристическое свойство показательного закона надежности

Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Это объясняется тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Пусть – безотказная работа элемента на интервале длительностью .

– безотказная работа элемента на интервале длительностью .

Тогда – безотказная работа на интервале длительностью .

Найдем вероятности этих событий.

;

;

.

Найдем условную вероятность того, что элемент будет работать безотказно на интервале при условии, что он уже проработал безотказно на предшествующем интервале .

Эта вероятность найдется из формулы умножения вероятностей.

,

.

Полученная вероятность не содержит , а содержит только – это и означает справедливость указанного свойства.

Это схема внезапных отказов. Устройство не изнашивается, не стареет, а отказывает внезапно.

Нормальное распределение

Нормальным Гауссовым называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

Видим, что нормальное распределение определяется двумя параметрами т и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение.

Вычислим математическое ожидание.

0

интеграл Пуассона

.

Итак, имеет смысл математического ожидания.

Найдем теперь дисперсию.

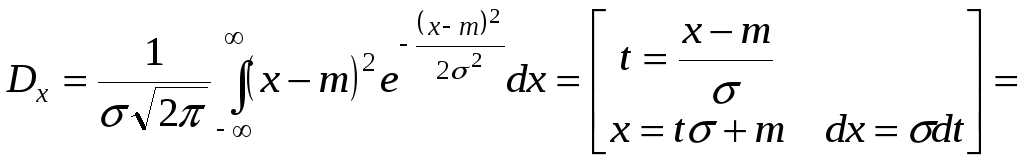
вычисляя по частям

.

, ,

т.е. – имеет смысл с.к.о.

Вычисляя моменты, найдем

,

.

Если параметры , , то такое распределение называется нормированным, его плотность вероятности определяется выражением

.

Она табулирована.

Напомним, что

называется функцией Лапласа. Она табулирована. Ее основные свойства:

1) – монотонно возрастающая.

2) .

3) , т.е. нечетная

4) .

Вычислим вероятность попадания случайной величины, распределенной по нормальному закону в интервал :

.

.

Пример. По автостраде шириной 20м ведется стрельба по направлению ей перпендикулярном. Прицеливание по середине. Известно, что м. имеется систематическая ошибка в направлении стрельбы – недолет 3м. Найти вероятность попадания в автостраду при одном выстреле.

Р

у

ешение.

т=–3

–10

+10

х

Нас интересует – случайная величина – абсцисса попадания снаряда. Эта случайная величина распределена по нормальному закону с параметрами , . Таким образом, попадание в автостраду – это попадание случайной величины в интервал .

0,7571.

Рассмотрим интервал, симметричный относительно математического ожидания и найдем вероятность в этот интервал.

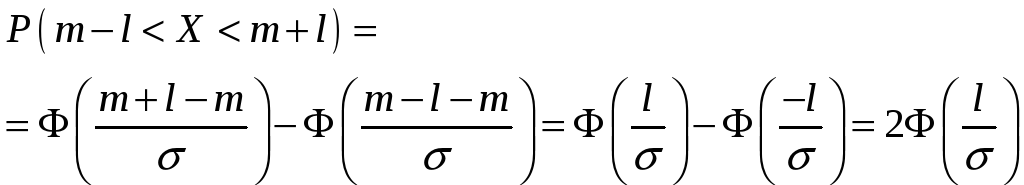
или

.

Если положить , то получим

.

Отсюда следует, что почти все значения (99,73%) нормально распределенной случайной величины попадают в интервал . Этот факт называют «правилом трех сигм». Интервал называется зоной практического рассеивания.

Пример. Технологической операцией предусмотрено изготовление изделий с симметричным относительно расчетного значения полем допуска шириной 0,3. определить, сколько будет получаться в среднем точных изделий с симметричным полем допуска шириной 0,05.

Решение.

,

.

, т.е. 38,3%.

Локальная и интегральная теоремы Муавра-Лапласа

Для вычисления вероятности успехов в испытаниях по схеме Бернулли мы получили формулу

и отметили трудоемкость ее применения при больших .

Приняв некоторые допущения при больших , а именно , , получили формулу Пуассона

.

И отметили, что ее обычно используют при и . Такое приближение называют асимптотикой Пуассона.

Покажем как можно вычислять подобные вероятности, основываясь на формулах нормального распределения. Говорят в этом случае об асимптоте Муавра-Лапласа.

Пусть число испытаний по схеме Бернулли велико, тогда для вероятности успехов справедлива следующая приближенная формула:

,

где , .

Ранее мы ввели нормированную (стандартную) функцию плотности нормального распределения

.

Пользуясь этой функцией, нетрудно получить такую формулу:

, (1)

где , , .

Формулу (1) называют локальной формулой Муавра-Лапласа.

Используя формулу (1), можно записать выражение для верности того, что число успехов заключено между числами и .

,

где , .

Выражение справа можно записать, используя функцию Лапласа и получим формулу, называемую интегральной формулой Лапласа.

.

Обычно формулы Муавра-Лапласа применяются в качестве приближенных формул при и .

Пример 1. Вероятность попадания в цель при одном выстреле равна 0,8. Определить вероятность того, что при 400 выстрелах произойдет ровно 300 попаданий.

Решение. ,

.

,

находим по таблицам .

0,0022.

Пример 2. Правильную игральную кость бросают 600 раз. найти вероятность того, что «двойка» выпадает от 90 до 120 раз.

Решение.

,

,

.

.

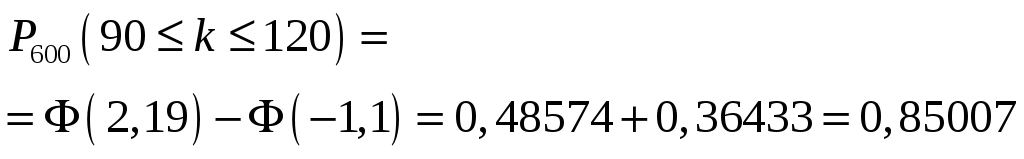Понятие о центральной предельной теореме

При знакомстве с законом больших чисел рассматривался «средний результат» большого числа случайных событий, но никак не затрагивался вопрос о предельном законе распределения при большом . Внимательное исследование этого вопроса показывает, что во многих случаях предельным законом выступает нормальный закон распределения.

Рассмотрим важный вопрос о причинах распространенности нормального закона, которая была замечена очень давно. Еще Гаусс пытался вывести нормальное распределение из некоторых формальных постулатов. В этом направлении и в дальнейшем были развернуты широкие исследования, продолжающиеся и сейчас. Работы, касающиеся условий, при которых возникает нормальное распределение, относятся к так называемой центральной предельной теореме.

Одним из следствий центральной предельной теоремы является локальная теорема Муавра-Лапласа, которая как раз утверждает, что

,

где , , – вероятность успеха в единичном испытании.

Иными словами при большом распределение Бернулли становится нормальным распределением.

Центральная предельная теорема существует во многих формах, но все они устанавливают условия, при которых возникает нормальный закон.

Впервые общий результат, который и называется центральной предельной теоремой, был получен Ляпуновым:

При сложении случайных величин с любыми законами распределения, но с ограниченными в совокупности дисперсиями, закон распределения суммы случайных величин при становится нормальным.

Ограниченность дисперсий означает, что ни одна из случайных величин не превалирует над другими, т.е. все слагаемые вносят примерно одинаковый вклад в сумму. Практически замена распределения суммы величин нормальным законом бывает уже правомочна при 10 – 15 слагаемых.

Примером практического приложения (на качественном уровне) может служить теория стрельб. Отклонение одной из координат от точки прицеливания с большой точностью можно считать нормально распределенной случайной величиной. Как это объясняется. Можно представить суммой - отклонений от различных причин.

1 – ошибка в изготовлении снаряда,

2 – ошибка в наводке,

3 – ошибка из-за скорости ветра,

4 – ошибка из-за атмосферного давления

и.т.д.

Этих факторов может быть очень много, каждый из них не превалирует над другими. Таким образом, выполняются условия центральной предельной теоремы.

Нормальный закон проявляется и в других областях деятельности, например, в теории ошибок измерений.

Когда-то нормальный закон считался единственным предельным законом, однако потом оказалось, что в некоторых массовых явлениях создаются условия для появления предельных законов распределения, отличных от нормального закона.