МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

ПРИ ВЫПОЛНЕНИИ ЛАБОРАТОРНЫХ РАБОТ ПО ОБЩЕМУ КУРСУ ФИЗИКИ

Измерения и погрешности измерений

Основная задача физического эксперимента заключается в измерении физических величин. Измерение − операция сравнения физической величины с величиной того же рода, принятой за единицу.

Различают измерения прямые и косвенные. К прямым измерениям относятся непосредственные измерения физических величин измерительными приборами (например измерение промежутка времени секундомером, силы тока амперметром и т.д.). К косвенным измерениям относятся измерения величин, связанных функциональной зависимостью с величинами, измеряемыми непосредственно. Например, плотность жидкости можно найти, разделив массу жидкости на ее объем. Масса жидкости и ее объем измеряются непосредственно.

Никакое измерение нельзя выполнить абсолютно точно, результат любого измерения всегда содержит погрешность. Поэтому необходимо знать, насколько полученный результат близок к истинному значению, т.е. указать точность измерения. Для этого вместе с полученным результатом указывают приближенную погрешность измерений. Например, запись x = 38 ±3 означает, что истинное значение величины х лежит, скорее всего, в пределах от 35 до 41. Оценивать и указывать точность результата измерений очень важно, без этого ценность результата часто равна нулю.

Погрешности измерений разделяют на систематические, случайные и промахи.

Систематические погрешности вызываются причинами, дей-

ствующими упорядоченным образом при многократном повторении измерений. Они приводят к отклонениям результатов измерений в одну сторону от истинного значения физической величины и остаются постоянными на протяжении всей серии измерений. Систематические погрешности могут быть следствием неточности приборов, погрешностей экспериментальной установки и т.п.

В принципе систематические погрешности можно устранить или учесть.

Случайные погрешности зависят от большого числа случайных факторов, действие которых в каждом опыте различно и не

2

может быть учтено. Случайные погрешности всегда присутствуют в эксперименте и служат причиной разброса результатов отдельных измерений при их многократном повторении. Имеются надежные способы уменьшения этих погрешностей. Например, увеличивая число измерений и находя среднее арифметическое результатов, мы будем получать величину, которая будет все ближе к истинному значению. Случайные погрешности являются неустранимыми, но с помощью теории вероятностей можно оценить их величину.

Промахи, или грубые погрешности, вызываются неисправностью приборов, невнимательностью экспериментатора и т.п. В большинстве случаев промахи хорошо заметны, так как соответствующие им цифровые отсчеты резко отличаются от других. При обработке результатов измерений такие отсчеты следует отбрасывать. Промах можно заметить только при многократном измерении одной и той же величины. Поэтому, какую бы величину вы ни измеряли, никогда не ограничивайтесь одним измерением. Для исключения промаха необходимо работать четко и внимательно, аккуратно записывая отсчеты.

Таким образом, результат каждого измерения содержит систематическую и случайную погрешности. Задача экспериментатора состоит в том, чтобы оценить их величины.

Прямые измерения

Случайные погрешности. Доверительный интервал и доверительная вероятность

Когда результат измерений представляет собой случайную величину и каждое измерение содержит случайную погрешность, то оценку точности этих измерений можно получить с помощью методов математической статистики.

Предположим, мы провели серию измерений некоторой физической величины x. Результат отдельного измерения обозначим xi, общее число измерений – n. Если систематическая погрешность отсутствует, разумно предположить, что значения xi расположатся вблизи неизвестного нам истинного значения x измеряемой величины, причем отклонения в сторону больших и меньших значений будут равновероятными. Тогда в качестве наилучшего приближения к истинному значению следует взять среднее арифметическое x отдельных измерений:

3

	n
x =	∑xi
	i=1	.	(1)
	n

Для упрощения вычислений в качестве приближенного значения измеряемой величины можно взять среднее между максимальным и минимальным значениями, полученными при измерениях:

x ≈	xmax + xmin	.	(2)
2

Точность соответствия среднего значения истинному значению зависит от ряда факторов и в первую очередь от точности каждого измерения и от числа измерений. Выполнив измерения, нужно привести результат и дать информацию о его точности. Принято указывать интервал значений измеряемой величины x ± x , в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины. Величина x называется абсолютной погрешностью результата; интервал от x − x до x + x – доверительным интервалом.

Для того чтобы приведенный доверительный интервал имел конкретный смысл, нужна количественная характеристика его достоверности. Такая характеристика (вероятность того, что среднее значение x отличается от истинного не более чем на x ) назы-

вается доверительной вероятностью или надежностью. Обозна-

чим ее α. Поясним смысл этой величины примером.

Пусть результат серии измерений записан в виде x = 38 ±3 и сказано, что приведенный доверительный интервал (от 35 до 41) соответствует доверительной вероятности α=0,9. Что это означает?

Если мы произведем серию измерений, например N=100 измерений, то в α N =90 случаях результаты будут отличаться от ис-

тинного значения измеряемой величины не более чем на x =3, а остальные результаты выйдут за пределы доверительного интервала. Но погрешность результата измерений недостаточно характеризует собой достоинство измерения. Она не позволяет оценить сравнительную точность нескольких разнородных величин. Например, результат измерения сопротивления проводника R=(28±2) Ом, результат измерения его длины L=(400±2) см. Что точнее измерено? Погрешности об этом ничего не говорят. В таких случаях вычисляют относительные погрешности, т.е. отношение погрешности к среднему результату измерений:

4

ε =	х	(3)
	x

ипроизводят их сравнение. В данном случае εR = 282 ≈0,07,

εL = 4002 =0,005; измерение длины выполнено точнее.

Относительная погрешность может быть выражена в процентах:

ε =	х	100% .	(3′)
	x

В данном примере εR =7%, εL =0,5%.

Окончательный результат приводится с указанием абсолютной и относительной погрешностей и доверительной вероятности:

x = ... ,

х = ... , εх = ... , α = ... .

Значащими цифрами называются все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность которой можно ручаться. Например, в числе 0,00385 три значащие цифры; в числе 0,003085 их четыре; в числе 2500 – четыре; в числе

2,5·103 – две.

Теория ошибок показывает, что нет смысла проводить вычисление погрешностей с большой точностью. Промежуточные вычисления погрешностей производят не более чем с двумя значащими цифрами. При записи результата измерения в стандартной форме достаточно ограничиться одной значащей цифрой в погрешности (т.е. округлить x до одной значащей цифры), но если первая значащая цифра – единица, нужно оставить две значащие цифры. После этого среднее значение x округляется так, чтобы в нем осталось столько же знаков после запятой, сколько их получилось в погрешности.

Примеры правильной записи результата измерения: x = (5,290±0,013) мм; x = (4,52±0,03) мм;

x = (7,2±0,8) мм; x = (49±3) мм.

Примеры неправильной записи результата измерения: x = (5,29±0,01) мм; x = (5,2900±0,0134) мм;

x = (5,29±0,013) мм; x = (4,521±0,032) мм; x = (7±0,8) мм.

5

Некоторые методы определения доверительного интервала

Метод Корнфельда. Доверительный интервал выбирается в пределах от минимального результата измерений до максимального:

x − х = хmin ;			x +			х = хmax .
Для x отсюда получаем формулу (2), а для						x – выражение
х =	хmax − xmin					.	(4)
		2
Как доказывается в теории, такому доверительному							интервалу
соответствует доверительная вероятность
		1		n−1
α =1−							(5)
		2

где n – число измерений в данной серии. Недостаток метода в том, что при заданном числе измерений мы не можем произвольно выбрать доверительную вероятность, ибо она ”жестко” определяется числом измерений n (см. формулу (5)).

Метод Стьюдента. В математической статистике разработан метод определения доверительного интервала с заданной доверительной вероятностью при любом числе измерений (в том числе и малом). Согласно этому методу в качестве лучшей меры точности

результата измерений взято среднеквадратичное отклонение σx ,

равное

	n
σx =	∑(xi − x)2
	i=1	.	(6)
	n(n −1)

Оно показывает, насколько может уклоняться от истинного значения x среднее арифметическое x наших измерений.

В теории ошибок интервал возможных значений величины обычно измеряют в единицах σx , т. е. x /σx = tα;n , где tα;n – коэффициент Стьюдента, зависящий от числа измерений n и от доверительной вероятности α.

Методы математической статистики позволяют рассчитать величину tα;n для различных доверительных вероятностей α и раз-

личных n; они приведены в таблице.

6

Пользуясь значениями коэффициента Стьюдента, можно найти доверительный интервал, в который попадает истинное значение измеряемой величины с заданной доверительной вероятностью, вычислив погрешность результата по формуле

x = tα;n σ x ,

(7)

или определить, сколько измерений необходимо провести, чтобы результат имел точность не ниже заданной.

Из таблицы, с учетом соотношения (7), видно, что чем больше доверительная вероятность α, тем шире доверительный интервал при данном числе измерений n и, наоборот, чем меньше α, тем уже доверительный интервал.

Значения коэффициентов Стьюдента tα,n

n			α
	0,6	0,8	0,9	0,95	0,98
2	1,38	3,08	6,31	12,71	31,82
3	1,06	1,89	2,92	4,30	6,97
4	0,98	1,64	2,35	3,18	4,54
5	0,94	1,53	2,13	2,78	3,75
6	0,92	1,48	2,02	2,57	3,37
7	0,91	1,44	1,94	2,45	3,14
8	0,90	1,42	1,90	2,37	3,00
9	0,89	1,40	1,86	2,31	2,90
10	0,88	1,38	1,84	2,26	2,82

Оценка систематической погрешности результата измерений

Систематические погрешности можно разделить на группы. Погрешности, природа которых нам известна, а величина может быть достаточнo точно определена, можно учесть при обработке результатов и исключить введением соответствующих по-

правок (исключенные систематические погрешности). Например,

если шкала линейки, которой производили измерение, начиналась не от нуля, то при отсчете нужно ввести соответствующую поправку.

Другую группу составляют погрешности, которые трудно исключить, ибо они зависят от многих факторов: погрешности метода, погрешности средств измерений и других (неисключенные систематические погрешности). Для средств измерений указыва-

7

ются предельные (т.е. максимальные) не исключенные систематические погрешности (приборные) – xприб .

Предельная систематическая погрешность (приборная) определяется по классу точности прибора или как половина цены наименьшего деления шкалы прибора, когда не указан класс точности. Погрешность при измерении штангенциркулем

или микрометром определяется как половина точности измерения, указанной на приборе. При взвешивании на весах предельная погрешность принимается равной половине массы наименьшей гири в разновесе.

Электромагнитные приборы обычно характеризуются клас-

сом точности в пределах от 0,1 до 4,0 (применяются следующие классы точности: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0). Так, если на при-

боре указан класс точности 0,5, то это означает, что при каждом измерении допускается погрешность, не большая, чем 0,5% от всей действующей шкалы прибора. Например, амперметр, шкала которого рассчитана на 500 мА, при классе точности 0,5 дает погрешность в измерении тока не более чем в 0,005×500 мА=2,5 мА, т. е.

xприб =0,01 k xмакс ,

где k – класс точности прибора; xмакс − предельное (максимальное) значение на шкале прибора (либо данного его диапазона, если прибор многопредельный), называемое пределом измерения прибора. Класс точности указывается на шкале прибора в виде соответствующих цифр (не заключенных в кружок). Если же эти цифры заключены в кружок, то

xприб =0,01 k xизм ,

где xизм – действительное значение измеряемой величины. Отсюда следует р е к о м е н д а ц и я : выбирать прибор (или шкалу многопредельного прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы (когда класс точности не обведен кружком).

Порядок обработки и форма представления результатов прямых измерений

1. Определяют среднее арифметическое из результатов измерений:

8

		1	n
x =			∑xi .
		n i=1
Величину x принимают за результат измерения.
2. Оценивают среднее квадратичное отклонение результатов
измерений
		n
σx =	∑(xi − x)2
	i=1			.
		n(n −1)
3. Находят случайную погрешность				xслуч , соответствующую
заданной доверительной вероятности α :
xслуч	= tα;n σx .

Коэффициент Стьюдента tα;n находят по таблице с учетом n и α. В

лабораторной практике употребляют значения α, равные 0,90; 0,95.

4. Определяют границу неисключенной систематической (при-

борной)	погрешности результата измерений xприб . Если одна из
величин	xслуч или xприб превышает другую в три и более раз,

то для дальнейших расчетов используют лишь большую из них. Если же xслуч ≈ xприб , находят полную погрешность:

x = ( xслуч )2 + ( xприб )2 .

5.Определяют относительную погрешность

εx = xx 100% .

6.Результат измерений представляют в стандартной форме:

x = x ± x, εx = ... %.

Косвенные измерения

Погрешности косвенных измерений

При косвенных измерениях искомая физическая величина связана некоторой функциональной зависимостью с рядом независимых друг от друга величин x1, x2, … , xm:

y = F(x1, x2, … , xm).

9

Величины xi измеряют непосредственно (прямо). Результат измерения каждой из величин хi содержит свою погрешность. И в зависимости от вида функции, связывающей искомую величину y с результатами измерений xi, эти погрешности по-разному влияют на погрешность окончательного результата.

Задача состоит в том, чтобы найти наивероятнейшее значение искомой величины у и оценить погрешность ее измерения. В качестве о ц е н к и величины у принимают величину, которая представляет собой значение функции, соответствующее средним зна-

чениям величин xi , т. е.

y = F(x1 , x2 ,..., xm ).

Результат косвенного измерения также содержит случайную и систематическую погрешности.

Общие правила вычисления погрешностей могут быть выведены с помощью дифференциального исчисления.

Пусть интересующая нас величина y линейно зависит от измеряемой величины x:

y=ax+b.

(8)

Здесь а и b – постоянные, точно известные величины. Легко показать, что если х изменить на x , то y, соответственно, изменится

на величину a x , т. е.
y = a x .	(9)
Если x – погрешность измерения, то	y будет погрешностью

результата.

В общем случае, если y=F(x), то для погрешностей, малых по сравнению с измеряемой величиной, мы можем с достаточной

точностью написать (так как y ≈ dy )
′	(10)
y = F (x) x ,

	′			x = x .
	где F (x) – производная по x, взятая при
	Из выражения (10) легко получаем относительную погреш-
	ность	F ′(x)
	y =		x ,
		F(x)
	y			′
	где F( x ) – есть значение у при x = x ;
				F (x) – производная по x,

взятая при x = x .

Если у – функция многих измеряемых величин x1 , x2 ,..., xn ,

т.е. y=F(x1, x2, ... , xn), то

10

y =

∂F

x +

∂F

x

+... +

∂F

x

n

,

(11)

∂x

∂x

∂x

1

2

2

n

∂F

∂F

1

где

,

и т. д. – есть частные производные от F по x1, x2, ... ,

∂x

∂x

2

1

xn. В математике правая часть выражения (11) называется полным дифференциалом функции нескольких независимых переменных, а

∂F

слагаемые ∂xi xi , из которых он состоит – частными дифферен-

циалами.

Но расчет по формуле (11) дал бы з а в ы ш е н н о е значение погрешности y , так как он не учитывает знак погрешностей.

В действительности погрешности разных знаков частично компенсируют друг друга и погрешность результата (при той же надежности) будет меньше рассчитанной по формуле (11). Теория вероятности дает следующий метод вычисления погрешности функции:

y = (

∂F x )2

+

( ∂F

x

2

)2 +... + ( ∂F

x

n

)2

,

(12)

1

∂x2

∂xn

∂x1

или в общем виде

.

n

( ∂F

y =

∑

xi )2

(13)

=

∂x

i

i

1

Относительная погрешность результата

y

n

1

∂F

=

∑(

xi )2 .

(14)

Так как

y

i=1

F

∂xi

1

∂F

∂ln F ,

=

F

∂xi

∂xi

то для относительной погрешности получаем

y

n

∂ln F

=

∑(

xi )2 .

(15)

y

i=1

∂xi

Из (15) или (14) вытекает последовательность операций для определения относительной погрешности.

П р и м е р. Экспериментально определяем плотность вещества

11

ρ = 4m lπD2

где m – масса тела в форме цилиндра; l – длина цилиндра; D – диаметр цилиндра; m, l, D измеряются непосредственно и имеют

погрешности m,

l, D;

π – не измеряется, но берется с некото-

рым приближением

π . Требуется определить

ρ .

Удобнее сначала определить относительную погрешность

ρ

по формуле (15). Для этого необходимо выполнить следующее.

ρ

1. Прологарифмировать функцию ρ :

ln ρ = ln 4 + ln m −ln l −lnπ − 2ln D .

2. Взять частные производные от ln ρ по m,

l, π, D:

∂ln ρ

=

1

;

∂ln ρ = −

1

;

∂m

m

l

∂l

∂ln ρ

= −

1

;

∂ln ρ

= −

2

.

∂π

π

∂D

D

3.Подставить полученные частные производные в выражение

(15)и записать относительную погрешность результата:

ρρ = ( mm)2 + ( ll )2 + ( ππ )2 + (2DD )2 .

Здесь полезно оценить вклад в общий результат погрешностей

π

прямых измерений. Если, например, π окажется значительно меньше максимальной погрешности, то ее можно отбросить. Во-

обще, при вычислении yy смело можно отбрасывать погрешно-

сти, не превышающие 13 от максимальной. При этом вычисления

упрощаются и становится очевидным, какие измерения надо производить более тщательно.

4. Определить абсолютную погрешность результата:

ρ = ρ (	m)2	+ (	l	l )2 + (	π )2	+ (2	D )2 .	(16)
	m				π		D

12

Погрешности в случае простейших функций. Если косвенно измеряемая величина выражается простейшей функцией, то используя указанный метод, можно вывести следующие зависимости для определения погрешностей:

если y = x1 + x2 или y = x1 − x2 , то из формулы (13) получим

			y = ( x			)2 + ( x	2		)2 ;
				1
если	y = ax x	2	или y = a	x1		, где а − постоянная величина, то
	1			x2
из формулы (14) или (15) получается
			y = y (	x1 )2 + ( x2 )2						;
				x		x		2
				1
если	y = ax n , где а − постоянная величина, то
			y = y n	x		= y (n x )2					;
				x			x

если y = an x , где а − постоянная величина, то y = y 1n xx = y ( nxx)2 .

П р и м е р: y = 4x12 x2 .

3 x3 x4

2

Пользуясь указанными соотношениями, легко определить абсолютную погрешность y не прибегая к дифференцированию:

y = y

(

2 x1 )2

+ (

x2

)2

+ (

x3 )2

+ 2(

x4

)2 .

x

2x

2

3x

3

3x

4

1

Обратите внимание, что в этом примере, как и в трех последних зависимостях, постоянный множитель a (здесь a = 4 ) не входит в формулу погрешности.

Порядок обработки и форма представления результатов косвенных измерений

1. Результаты измерений каждой из величин хi обрабатывают как прямые измерения и представляют в стандартной форме:

13

xi = xi ± xi , εxi = ... %.

2. Пользуясь средними значениями величин xi , находят оценку значения результата косвенного измерения y = f (x1 , x2 ,..., xn ).

3. Пользуясь соотношением (14) или (15), или зависимостями для определения погрешностей косвенных величин, выражаемых простейшими функциями, описанными выше, вычисляют величи-

ну	y	и находят y . Можно просто пользоваться формулой (13).
	y

4. Результат косвенного измерения представляют в стандартной форме:

y = y ± y , εy = ...%.

Графическое представление результатов измерений

Построение и оформление графиков

Часто в эксперименте изучается зависимость одной величины от другой, тогда результаты измерений могут быть представлены графически. Графики дают наглядное представление о виде функциональной зависимости, выявляют многие ее важные свойства и особенности. При построении графиков руководствуются следующими правилами.

1.По оси абсцисс всегда откладывают ту величину, которая является причиной изменения другой (т.е. аргумент). По оси ординат откладывают функцию.

2.Для каждой из величин определяют диапазон в котором она изменяется и затем подбирают масштаб, в котором эта величина будет изображаться на оси. Масштаб должен быть простым, шкала должна легко читаться, т.е. единица масштаба должна соответствовать ”круглому” числу измеряемой величины (1, 2, 5, 10 или те

же цифры, умноженные на 10 ±n ). Масштаб должен быть таким, чтобы погрешность измерений представлялась на графике отрезком заметной длины. Единица масштаба должна равняться ”круглому” числу миллиметров (1, 2, 5, 10 и т. п.) чтобы легко можно было откладывать десятые и сотые доли.

3. На каждой оси графика обязательно наносят шкалу с ”круглыми” числами измеряемой величины.

14

4.На осях графика следует указывать название (или символ) и единицы измерения величин.

5.Экспериментальные результаты представляют на графике в

виде точек, обводя их кружком или другим знаком ( ,Ο,+). Точки, относящиеся к различным группам опытов, обозначают разными знаками. Погрешности указывают для одной или для обеих измеряемых величин в виде отрезков длиной в доверительный интервал (рис. 1).

Чтобы не загромождать график, делают это в следующих случаях: при построении кривой по экспериментальным точкам; при сравнении экспериментальных данных с теоретической кривой.

6. В соответствии с экспериментальными точками проводят ”наилучшую” кривую, проходящую через доверительные интервалы возможно ближе к экспериментальным точкам. Не следует соединять точки ломаной линией. Обычно физические зависимости соответствуют гладким, плавно меняющимся

Рис. 1 функциям. На каждом участке графика точки должны располагаться примерно поровну по обеим сторонам кривой. При построении кривой следует учиты-

вать погрешности измерений.

7. Графики снабжают заголовками и пояснениями, содержащими точное и краткое описание того, что показывает график. Заголовок и пояснения располагают под графиком или на самом графике – на свободном от кривых и экспериментальных точек месте.

Графический анализ данных

Сравнение с теорией. Для проверки теоретической зависимости на график наносят экспериментальные точки с указанием погрешностей, а также строят теоретическую кривую. В зависимости от того, пройдет ли кривая через доверительные интервалы экспериментальных точек, результаты эксперимента признают согласующимися (а) или несогласующимися (б) с теорией (рис. 2).

15

Рис. 2

Подбор параметров. Часто экспериментально определяются величины х и у, связанные функциональной зависимостью

y = f (x, a1 , a2 , ...).

Вид функции f(x) бывает обычно известен из теоретических соображений, а параметры ai определяются по результатам эксперимента. В

случае линейной зависимости есть простые приемы нахождения параметров, позволяющие построить ''наилучшую'' прямую. Пусть между хi и

уi предполагается линейная зависимость y = kx +b и требуется опреде-

лить параметры k и b, наиболее соответствующие результатам измерений.

Для приближенного определения параметров нужно нанести экспериментальные точки на график и провести прямую так, чтобы по обе стороны от нее оказалось одинаковое количество точек и отклонения точек от прямой были бы минимальны. Угловой коэффициент k определяется из графика или вычисляется через координаты крайних экспериментальных точек:

k = yn − y1 . xn − x1

Погрешность находят по формуле

k =			y	,
	x	n	− x
			1

где у – погрешность в определении у. Если погрешность измерения у неизвестна, в качестве у следует взять наибольшее отклонение точек от проведенной прямой. Для более точного определения k воспользуемся методом парных точек. Пронумеруем экспериментальные точки (рис.3),

16

возьмем две из них, например 1 и 4, проведем через них прямую. Эта прямая имеет угловой коэффициент

k1 = y4 − y1 . xi − x1

Рис. 3

Возьмем другую пару точек – 2 и 5, снова построим прямую и определим ее угловой коэффициент k2. Проведя таким образом еще несколько прямых, получим набор значений угловых коэффициентов. Их среднее значение даст угловой коэффициент k искомой прямой, которая и будет ''наилучшей''. Погрешность k определяется так же, как и погрешность среднего значения серии измерений.

Точки для проведения вспомогательных прямых следует выбирать так, чтобы расстояния между координатами хi этих точек были для всех прямых одинаковыми и немного превышали половину всего интервала значений величины х. При этом точность определения k будет наибольшей.

Вспомогательные прямые на графике обычно не проводят, а ограничиваются лишь вычислением угловых коэффициентов. На графике строят только ''наилучшую'' прямую.

Для нахождения b нужно учесть, что наилучшая прямая должна проходить через центр тяжести экспериментальных точек, т. е. через точку с координатами

x =	1 ∑xi ; y =	1 ∑yi .
	n	n
	n i=1	n i=1

Из уравнения прямой находим

b = y −kx.

При построении наилучшей прямой измеренные значения х обычно считают точными. Тогда погрешность определения b

b = ( y)2 + (x k)2 .

В качестве грубой оценки y используем максимальное отклонение точек от проведенной прямой.

17

Обработка результатов измерений методом наименьших квадратов

Между измеряемыми величинами (например, хi и уi, где i − номер измерения) часто существует функциональная зависимость. Пусть вид этой зависимости известен с точностью до значений некоторых параметров а1,

а2, ... , аm

y= f (x, a1 , ... , am )

инужно подобрать значения параметров так, чтобы расхождение расчет-

ной кривой с результатами опыта было минимальным.

Критерием получения ''наилучшей'' комбинации параметров служит минимальность суммы квадратов отклонений или среднеквадратичного отклонения экспериментальных точек от расчетной кривой. Подбор параметров по такому принципу называется методом наименьших квадра-

тов (МНК).

МНК не дает вида зависимости у(х). Вид зависимости выбирается либо из теоретических предположений, либо как наиболее соответствующий экспериментальным данным. Поэтому перед применением МНК необходимо убедиться, что результаты опыта действительно соответствуют предполагаемой зависимости. Прежде всего нужно представить результаты графически.

При интерпретации опытных данных значения хi будем считать точными. Погрешности в определении х приводят к дополнительному разбросу уi и тем самым учитываются в отклонениях уi от расчетной кривой.

Критерий МНК требует минимальности суммы

	n			2
S = ∑[yi			− f (xi , a1 , ... , am )] .
	i=1
Условие минимума	∂S	= 0 при i=1,		... , m содержит m уравнений,
	∂ai

т.е. столько, сколько неизвестных параметров аi.

Применим МНК к линейной зависимости, которая в нашем практикуме часто встречается:

y = kx +b.

Сумма

	n
	S = ∑( yi	−kxi −b)2	(17)
минимальна при условии	i=1
∂S = −2∑xi ( yi −kxi −b) = 0;
	m
∂k	i=1
∂S = −2∑( yi − kxi − b) = 0.
	m
∂b	i=1
Отсюда приходим к уравнениям

18

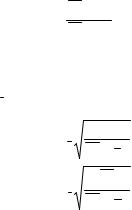
m		m		m
∑xi yi	= k∑xi		2	+b∑xi ;
i=1		i=1		i=1
m		m
∑yi		= k∑xi		+ mb.
i=1		i=1

Разделив обе части уравнений на m, получим

xy	= k x2 +bx;			(18)
y = kx +b.				(19)

Из последнего уравнения следует, что наилучшая прямая проходит через центр тяжести экспериментальных точек, т. е. через точку с координатами x, y.

Решение уравнений (18) и (19) дает следующие выражения для параметров прямой:

k= xy − xy ;

x2 − x 2

b = y −kx.

Выражения среднеквадратичных отклонений приводим без вывода:

				1		m
	σ y	=			∑( yi		− kxi −b)2 ;
			n(n −1)
						i=1
			σk	=σ y			1	;
						x2	− x 2
			σb	=σ y		x2		.
						x2	− x 2

Если экспериментальные точки группируются вдали от начала координат, то вычисления должны проводиться с большей точностью, без округлений.

Вычисления по МНК обычно проводят на ЭВМ, используя стандартные программы. В результате вычислений следует написать уравнение прямой и провести ее на графике.

Это и будет расчетная линия, имеющая наименьшее расхождение с результатами эксперимента.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособие для вту-

зов. – 2-е изд., испр. и доп. – М.: Высш. шк., 1999. С. 683-687.

ЛАБОРАТОРНАЯ РАБОТА № 1

19

ОЗНАКОМЛЕНИЕ С ИНСТРУМЕНТАМИ ДЛЯ ИЗМЕРЕНИЯ ЛИНЕЙНЫХ ВЕЛИЧИН. ОПРЕДЕЛЕ-

НИЕ ОБЪЕМНОЙ ПЛОТНОСТИ ВЕЩЕСТВА

Приборы и принадлежности: штангенциркуль, микрометр, лабораторные весы, измеряемые тела.

Цель работы: освоение алгоритма расчета ошибки для прямых и косвенных измерений на примере определения объемной плотности вещества; приобретение навыков работы с микрометром, штангенциркулем и лабораторными весами.

Краткая теория

Измеряя длину какого-либо тела миллиметровым масштабом, можно поручиться лишь за цифры, обозначающие число целых миллиметров. Относительно десятых долей миллиметра можно сказать, что при оценке их на глаз максимальная ошибка не превосходит половины цены деления шкалы, т.е. половины длины ее наименьшего деления. Таким образом, максимальная ошибка равна 0,5 мм, если шкала разделена на миллиметры.

Для того чтобы можно было получить линейные размеры, снятые с точностью до десятых долей миллиметра (а иногда и до сотых), пользуются так называемым нониусом.

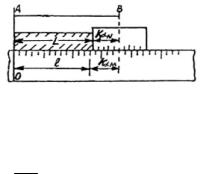
Линейный нониус – это небольшая линейка, разделенная на 10, 20, 25 или 50 делений, которая может скользить вдоль основной масштабной шкалы. Указанные

деления наносятся так, что n − 1 деление основной масштабной шкалы равняются по длине n делениям нониуса (рис. 1.1).

Если αN и αM − соответст-	Рис. 1.1.
венно цены делений нониуса и
основной шкалы (масштабной), то	nαN = (n −1)αM . Разность

αM −αN , называемая точностью нониуса, равна

αM −αN = αnM .

Если, например, основная шкала разделена на миллиметры, а на нониусе 10 делений, то мерой его точности будет 0,1 мм. Точность нониуса равна добавке длины (после целых миллиметров),

20

которую обозначает одно деление на нониусе; или, другими словами, точность нониуса равна цене деления нониуса, в том смысле, что обозначает это деление (но не в том смысле, что обознача-

ет αN ).

Практическое пользование нониусом крайне просто. Для этого к нулевому делению основной шкалы прикладывают один конец измеряемого тела, а к другому его концу нониус (см.

рис. 1.1).

Отсчитав по шкале число целых делений l, занимаемых телом длиной L, смотрят, какое по номеру деление нониуса k совпадает или ближе всего подходит к какому-либо делению основной шкалы.

Например, на рис. 1.1 l=13 и k=5. Так как в данном случае n=10 делений нониуса умещаются на девяти делениях шкалы, а

цена деления шкалы, допустим, равна αM =1 мм, то точность но-

ниуса αnM = 0,1 мм. Практически отсчет производят так: умножив

13 на 1, а 5 на 0,1 и сложив оба числа, получают длину тела, равную 13,5 мм.

В общем случае (см. рис. 1.1) получим соотношение

АВ = (l +k)αM = L +kαN ,

откуда L = lαM +k(αM −αN ) или L = (l + kn)αМ .

Увеличить точность линейных измерений можно, применяя микрометрический винт. Он состоит из полого стержня 2 (рис. 1.2), внутрь которого ввинчен винт 1, связанный с барабаном 3.

При вращении винта происходит вращение барабана и одновременно его перемещение относительно стержня 2. Отсчет ведется по горизонтальным шкалам и

Рис. 2.2. круговой шкале барабана. Горизонтальные шкалы расположены по обе стороны продоль-

ной черты, нанесенной по длине стержня.

21

Цена деления каждой шкалы 1 мм. Верхняя шкала смещена относительно нижней шкалы на 0,5 мм, что позволяет с помощью этих шкал произвести измерения с точностью до 0,5 мм. Сотые доли миллиметра отсчитывают по круговой шкале барабана, определив предварительно цену ее деления α (точность):

α = hn ,

где h – шаг микрометрического винта, показывающий, на сколько делений при поступательном перемещении сместится микровинт за один полный оборот барабана; n − число делений на барабане.

Число сотых долей соответствует делению шкалы, расположенному против продольной черты на стержне. Чтобы получить длину измеряемого тела, к показаниям, снятым по горизонтальным шкалам, прибавляют показания, снятые с круговой шкалы. Например, на рис. 1.2 показания микрометрического винта 5,85 мм: по первой шкале число целых миллиметров 5, прибавляем 0,5 мм со второй шкалы, а сотые доли миллиметра снимаем по круговому барабану (0,35 мм).

Таким образом, нониус и микрометрический винт применяются для более точного измерения линейных размеров.

Объемной плотностью вещества называют отношение массы тела к его объему:

ρ = Vm .

Вычисление объема тела зависит от его формы. Например, если тело в форме параллелепипеда, то V=ldh, где l, d и h – соответственно длина, ширина и высота параллелепипеда. Тогда

ρ =		m	.		(1.1)
Если тело в форме цилиндра, то		ldh
		4m
ρ =				,	(1.2)

πD2l

где l и D – соответственно длина и диаметр цилиндра.

Все величины для вычисления ρ являются результатами прямых измерений.

22