ТФКП и операционные исчисления

61. Разложить в ряд по степеням

ге z < 1 .

62. Разложить в ряд по степеням

0 < z < 2 .

63. Разложить в ряд по степеням

ласти 1 < z +1 < ∞ .

z	функцию	f (z) =				1			в кру-
				(z − 2)2
		1
z	функцию f (z) =						в		кольце
			z(z − 2)
z+1 функцию		f (z) =				z −1				в об-
						z(z + 2)

64. Разложить в ряд по степеням			z следующие функции:
1)	f (z) = cos2z ;	2)	f (z) = sin(2z −1).
65. Разложить в ряд по степеням			z –a следующие функции:
1)	f (z) = e3z−2 , a=1;	2)	f (z) = sin(z + i), a=i;

3)f (z) = z cos2z ; a=1;

4)f (z) = z 5 − z 3 + 2z − 3, a = 2 .

Часть Б

66. Разложить в ряд Тейлора по степеням z

функцию

f (z) =

z

, ис-

z2 + i

пользуя готовое разложение.

1

67. Разложить в ряд Тейлора по степеням z

функцию

f (z) =

, ис-

4 − z2

пользуя готовое разложение.

68. Разложить в ряд Лорана в области 0 <

z − a

< ∞ следующие функции:

1

f (z) = (z +1)sin

1

1)

f (z) = e

z2

, a=0;

2)

, a=-1;

1

z +1

3)

f (z) = (z + i)

2

cos

, a=-i.

z + i

1

69. Разложить в ряд

по степеням

z функцию

f (z) =

в области

z(z + 2)

z < 1.

9

70. Разложить в ряд

по степеням

z

функцию

f (z) =

z + 1

;

в

z2 − 3z + 2

области 2 <

z

< ∞ .

1

71. Разложить в ряд

по степеням

z–2

функцию

f (z) =

в

(z +1)(z − 2)2

области z −1 < 3 .

Изолированные особые точки аналитической функции комплексной пе-

ременной и их вычеты

		Часть А
72. Найти нули функции и указать их порядок:
1)	f (z) = (z3 − 1)2 ;	2)	f (z) = sin 2z ;
3)	f (z) = ctg 2 z ;	4)	f (z) = (z2 + 4z + 4)3 .

73. Найти особые точки, выяснить их тип и вычислить вычеты относи-

тельно особых точек следующих функций:

f (z) =

z

2) f (z) =

z2 +1

1)

;

;

(z +1)(z − 3)

z(1− z)

3)

f (z) =

z + 1

;

4)

f (z) =

cos z

;

z2

π

z − 2

5)

f (z) =

1

;

6) f (z) =

sin 3z

;

z3 + z

(z − πi)3

f (z) =

z2

8) f (z) = e

z

7)

;

1−z

;

ez + 3

z + 2

9)

f (z) =

z

;

10)

f (z) =

;

sin z

z5 − z3

z−

1

z2

11)

f (z) = e

z

;

12)

f (z) =

.

(z2 +1)2

10

Часть Б

74. Найти особые точки, выяснить их тип и вычислить вычеты относи-

тельно особых точек следующих функций:

1)

f (z) =

z + 4

;

2) f (z) =

z - i

;

z2 + 2z - 8

(z + i)(z - 2i)

3)

f (z) =

2z2 +1

;

4) f (z) =

2z + 5

;

(z - 2)3

z4

- 4z2 + 4

5)

f (z) =

z + 2

;

6) f (z) =

cos 2z

;

(z2 -1)2

æ

-

π

öæ

-

π

ö2

ç z

4

֍ z

2

÷

è

øè

ø

7)

f (z) =

sin z

;

8)

f (z) = sin

1

.

z2 (z - π )

z

Вычисление интегралов с помощью вычетов

Часть А

75. Вычислить следующие интегралы:

cos z dz

1)

ò

2z + i

dz ;

2)

ò

;

z(z - i)

z

2

- 2z - 3

z −i

=1,5

z

=2

ò

z2 - 3

ò

z

3)

dz ;

4)

dz ;

z(z + 2i)2

(z +1)2

z

=1

z + 2

=2

ò

sin z

ò

z2 + z -1

5)

dz ;

6)

dz ;

z

(z - 2i)3

=2

z2 (z -1)

=3

z−1+i

76. Вычислить интеграл

ò

z dz

,

где L

– прямоугольник с вершина-

cos z

L

ми в точках: z1 = -i ; z2 = 2 - i ; z3 = 2 + i ;

z4

= i .

77. Вычислить следующие интегралы:

ò

2z + i

òz

3

1

1)

dz ;

2)

e z dz ;

z3

+ z2

z

=2

z

=1

11

sin

iπz

−

z

πi

2

3)

ò

dz ;

4)

òe

z

+1

dz ;

z(z2

+1)

z −i

=1,5

z

=2

5)

ò

z dz

;

sin z(1- cos z)

z

=5

78. Вычислить следующие несобственные интегралы:

∞

dx

∞

x

2dx

1) ò

.

2)

ò

.

(x2 + 25)2

(x2 +16)2

−∞

−∞

∞

dx

∞

xdx

3) ò

.

4) ò

.

x2 - 2x +10

(x2 + 2x + 2)2

−∞

−∞

Часть Б

79. Вычислить следующие интегралы:

ò

(z +1)dz

ò

z2 - 2

dz ;

1)

;

2)

=4

z2 + 3z - 4

z

(z + i)(z - 3)2

z + 2

=2

3)

ò

z - i

dz ;

4)

ò

z dz

;

=1

(z +1)(z - 2i)2

=2

(z + 2)2 (z - 3)3

z −2i

z + 2

z

cos z dz

5) òe1−z dz ;

6)

ò

;

æ

π

ö2

z

=2

z −

π

=2

zç z

-

2

÷

2

è

ø

òz +1

7)z−i =1 z 2 - iz + 2(z - i)dz .

80. Вычислить интеграл	ò	ezi dz		;			где	L	–	ромб с вершинами в точках:
		sin 2z
	L
z1 = 2 ; z2 = i ; z3 = -2 ; z4 = -i .
	1
81. Вычислить интеграл	òz sin					dz ,		где	L	–	прямоугольник с верши-
			z2
	L
нами в точках: z1 = 1 + i ;	z2 = -1 + i ;						z3 = 1 - 2i ;				z4 = -1 - 2i .

12

82. Вычислить следующие несобственные интегралы:

∞

dx

∞

dx

1) ò

;

2) ò

;

(x2 +1)3

x2 - 2x + 50

−∞

−∞

∞

xdx

∞ x

2 +1

3) ò

;

4) ò

dx

(x

2

+ 4x +13)

2

x

4

−∞

0

+1

Функция-оригинал. Нахождение изображений по заданному оригиналу

Часть А

83. Какие из данных функций являются оригиналами (первое свойство функции- оригинала считается выполненным):

			1
1) ln(t + 3) ; 2)				; 3) cost2 ;		4) e t		3	.
		t2	- 4
84. Найти	изображение функций, используя определение преобразования
Лапласа:
1) f (t) = t +1 ;					ì2 - t,	0 < t £ 2;
				2) f (t) = í				t > 2.
					î 0,
85. Пользуясь теоремой смещения, найти изображения функций:
1)	f (t) = e3tch2t;			2)	f (t) = e−2t cos2 t;
3)	f (t) = e−0,5tt2;			4)	f (t) = sh2t sin 4t .

86. Пользуясь теоремой дифференцирования изображения, найти изобра-

жения функций:			f (t) = tshωt;
1)	f (t) = tch3t;	2)
3)	f (t) = t2e2t ;	4)	f (t) = t 2 sin 4t .

87. Пользуясь теоремой интегрирования изображения, найти изображения

функций:		e−at					2 t
1)	f (t) =		sin t	;	2) f (t) =	sin		;
		t				t
3)	f (t) =	e2t - e4t			.
		t

88. Пользуясь теоремой запаздывания, найти изображения функций:

1) f (t - 4) = et−4;	æ	π ö		æ	π ö
	2) f çt -	8	÷	= sinç2t -	4	÷;
	è		ø	è		ø

13

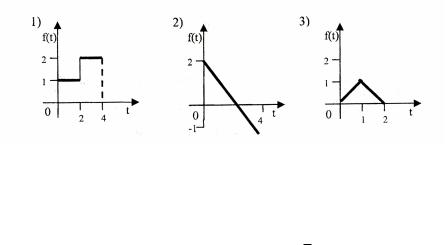
		æ	4	ö
	3) f (t − 2,5) = ch(2t − 5);	4) f çt -		÷	= sh(3t - 4) .
			3
		è		ø

89. Пользуясь теоремой дифференцирования оригинала, найти изображе-

ния f ′(t) , если:
1)	f (t) = cos 2t + t sin 2t;	2) f (t) = sin2 t;
3)	f (t) = e−3t cost;	4)	f (t) = tsh4t .
90. Найти изображения дифференциальных выражений:
1)	x′′(t) + 4x′(t) + 2x(t) ,	x(0) = 1,	x′(0) = -2 ;
2)	2x′′′(t) - 3x′′(t) +1,	x(0) = -1,	x′(0) = 1, x′′(0) = 0 .

91. Пользуясь теоремой умножения изображения, найти изображения функций:

t	t
1) f (t) = òcos 2(t -τ ) chτ dτ ;	2) f (t) = ò(t -τ )2 sin 3τ dτ ;
0	0
t

3) f (t) = òe−2(t−τ ) (1- 2τ )dτ .

0

92. Найти изображения функций, заданных графически:

Часть Б

93.Найти изображения функций:

1)f (t) = 2e−t cos 2t - 0,5sin 2t;

3)	f (t) =	sin 2t		-	t cos 2t	;
	4		2
5)	f (t) = e−2t sin 4t sin 3t;
7)	f (t) = t2 (et		- sht)cos3t;

2)f (t) = cht cos 4t;

4)f (t) = 32 t3e−2t ;

6)f (t) = te2t sin 3t;

8)f (t - 2) = 0,5(t - 2)et−2 ;

14

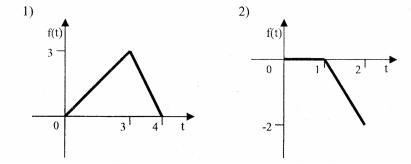
9)	f (t − 2) = e−2t cos 4(t − 2);			10)	f (t) =	sh2t		;
							t
		1− eat
11)	f (t) =		;	12)	f (t) =		cosbt − cos at		;
		tet						t
		t				t
13)	f (t) = ò(t −τ ) cos2 τ dτ ;			14)	f (t) = òsh(t −τ )e−4τ dτ .
		0				0

94.Найти изображения функций, заданных графически:

Нахождение оригиналов по заданному изображению

Часть А

95. Найти оригиналы для заданных функций:

p − 2

p

2

1) F( p) =

+

;

2) F( p) =

;

p2 + 4

p2 + 9

p2 − 4 p +13

3) F( p) =

1

4) F( p) =

p −1

;

.

p2 − 4 p + 20

p2 + 6 p +13

96. Используя теорему запаздывания, найти оригиналы для заданных

функций:	e−2 p		e−3 p				e− p p
1) F( p) =		; 2) F( p) =			; 3) F( p) =			.
	p + 5		p2	+1		p2	+ 3p + 2

97. Используя разложение дробей на простейшие, найти оригиналы для

	заданных функций:				p2
	1) F( p) =	p +1	;	2) F( p) =		+1		;
		p( p + 2)			p( p +1)( p		+ 2)

15

3) F( p) =

1

4) F( p) =

p − 3

;

.

p2 ( p +1)

p3 + 4 p2 + 4 p

98. Найти оригиналы для изображений с помощью теории вычетов:

1) F( p) =

p + 2

;

2) F( p) =

p2 + 2

;

( p +1)( p2 + 2 p −

3)

( p −1)( p2

+ 4)

3) F( p) =

p + 4

;

4) F( p) =

2 p −1

;

p3 − 4 p2 + 5 p

( p −1)2 ( p − 2)

5) F( p) =

p

;

6) F( p) =

p3 + 2 p + 2

.

( p +1)2 ( p2 +

4)

p3( p +1)

Часть Б

99. Найти оригиналы для заданных изображений:

p

3

2

1) F( p) =

+

;

2) F( p) =

;

p2 − 9

p2 −16

p2 + 4 p + 7

3) F( p) =

3p −1

;

4) F( p) =

4 − p − p2

;

p2 − 4 p + 3

p3 − p2

5) F( p) =

e− p ( p +1)

;

6) F( p) =

e−2 p p

;

p2 − 2 p +

5

p

2 + 4 p + 20

7) F( p) =

p −1

;

8) F( p) =

p2 +1

;

p4 + 5 p2 + 4

( p +1)( p + 3)( p + 5)

9) F( p) =

2 p − 3

;

( p2 + 4 p + 3)( p2 + 6 p + 8)

10) F( p) =

p + 2

;

11) F( p) =

2 p2 − p −1

;

p3 + 6 p2 + 9 p

p3 + 2 p2 + 2 p +1

12) F( p) =

p

.

( p −1)3 ( p +1)2

16

Приложения операционного исчисления

Часть А

100. Решить дифференциальные уравнения при заданных начальных усло- виях:

1)

x¢¢ - 3x¢ + 2x = 2e3t , x(0) = 1,

x′(0) = 3 ;

2)

x′′ - x′ = 2(1- t) ,

x(0) = 0 ,

x′(0) = 0 ;

3)

x¢¢ + 2x¢ + x = te−t ,

x(0) = -1 ,

x′(0) = 0 ;

4)

x′′ - 2x′ + 2x = 2t ,

x(0)

= 0 ,

x′(0) = -1;

5)

x¢¢ + x¢ = t3 + 6t ,

x(0) = 0 ,

x′(0) = 0 ;

6)

2x′′ + 3x′ = 2sin t ,

x(0) = 0 ,

x′(0) = -1;

7)

x′′ - 9x = sht ,

x(0) = -1 ,

x′(0) = 3 ;

¢¢ -

¢ =

ì −t

,

0

< t < 1

=

′

=

8)

x

x

ïe

,

x(0)

0 ,

0 ;

í

x (0)

ï

t ³ 1

î0,

9) x¢¢¢ - x¢¢ = 10e2t , x(0) = 0 , x′(0) = 0 , x′′(0) = 0 ;

10) x¢¢¢ - 3x¢¢ + 3x¢ - x = et , x(0) = 1, x′(0) = -1, x′′(0) = 1 .

101. Решить систему дифференциальных уравнений при заданных на-

чальных условиях:

1)

ìx¢

= x + 2y,

x(0) = 0 ,

y(0) = 5 ;

í

îy¢ = 2x + y +1;

2)

ìx¢¢ - y¢ = 0,

x(0)

= -

1 ,

′

=

y(0)

=

′

= -

í

x (0)

y (0)

1 ;

îx - y¢¢ = 2sin t;

ì

- x + y = 1,5t

2

,

3)

ïx¢

x(0)

= 0 , y(0) = 0 .

í

¢

ï

+ 4x + 2y = 4t +1;

îy

102. Решить интегральные уравнения типа свертки:

t

t

1)

òcos(t -τ )x(τ )dτ = sht ;

2)

òe−(t−τ ) x(τ )dτ = sin t ;

0

0

t

t

3)

t - ò(t -τ )x(τ )dτ = x(t) ;

4)

òsh(t -τ )x(τ )dτ = 1- cost ;

0

0

t

5)

òch(t -τ )x(τ )dτ = cht - cost ;

0

17

Часть Б

103. Решить дифференциальные уравнения при заданных начальных ус- ловиях:

1)

x¢¢ + x¢ - 2x = e−t ,

x(0)

= 0 , x′(0) = 1 ;

2)

x¢¢ + 4x¢ + 4x = t3e−2t

,

x(0) = 1,

x′(0) = 2 ;

3)

x¢¢ - 2x¢ = et (t2 + t - 3) ,

x(0) = 2 ,

x′(0) = 2 ;

4)

x¢¢ + 2x¢ + 2x = 2e−t sin t ,

x(0) = 1,

x′(0) = 1 ;

5)

x¢¢ + x¢ = sin t - 2e−t ,

x(0) = 0 ,

x′(0) = 0 ;

6)

x¢¢¢ - x¢ = 3(2 - t2 ) ,

x(0) = x′(0) = x′′(0)

= 1 ;

8)

x

¢¢ +

2x

+

x

¢ = ì1, 0 < t < 2

,

x(0)

=

′

=

0 ;

í

t ³

2

0 , x (0)

î3,

104. Решить систему дифференциальных уравнений при заданных началь-

ных условиях:

1)

ìx¢

- y¢ - 2x + 2y = 1- 2t,

x(0)

=

y(0)

=

′

=

0 ;

í

+ 2x¢ + x = 0;

y (0)

îx¢¢

ì

t

,

2)

ïx¢

+ y¢ - y = e

x(0)

= y(0)

= 0 ;

í

¢

¢

ï

+ y

+ 2y = cost;

î2x

ìx¢

= 2x - y - z,

3)

ï

x(0) = 1,

y(0) = 1,

z(0) = 0 .

íy¢ = x + z,

ï

îz¢ = -3x + y - 2z;

105. Решить интегральные уравнения типа свертки:

t

t

1)

òsh(t -τ )x(τ )dτ = 1- cost ;

2) 1+ òet−τ x(τ )dτ = x(t) ;

0

0

t

t

3) t3 + òsin(t -τ )x(τ )dτ = x(t) ;

4)

òcos(t -τ )x(τ )dτ = t cost .

0

0

18