Текст лекций по курсу

«Дискретная математика»

Оглавление

Типы графов 4

Маршруты и связность 7

Степени 9

Задача Рамсея 10

Экстремальные графы 12

Графы пересечений 14

Операции над графами 16

Блоки 20

Графы блоков и точек сочленения 20

Точки сочленения, мосты и блоки 21

Деревья 26

Описание деревьев 26

Центры и центроиды 29

Деревья блоков и точек сочленения 31

Независимые циклы и коциклы 31

Матроиды 35

Обходы графов 37

Эйлеровы графы 37

Гамильтоновы графы 38

Реберные графы 43

Некоторые свойства реберных графов 43

Характеризация реберных графов 46

Специальные реберные графы 50

Реберные графы и обходы 53

Тотальные графы 54

Раскраски 56

Хроматическое число 56

Теорема о пяти красках 58

Гипотеза четырех красок 59

Однозначно раскрашиваемые графы 62

Критические графы 65

Гомоморфизмы 67

Хроматический многочлен 69

Матрицы 73

Матрица смежностей 73

Матрица инциденций 74

Матрица циклов 75

Обзор дополнительных свойств матроидов 76

Связность 77

Связность и реберная связность 77

Орграфы 79

Орграфы и соединимость 79

Ориентированная двойственность и бесконтурные орграфы 80

Орграфы и матрицы 83

Турниры 85

Обзор по проблеме востановления турниров 86

Волновой алгоритм 87

Алгоритм Дейкстры 88

Алгоритм Флойда 89

Алгоритм Йена 90

Алгоритм Краскала 91

Типы графов

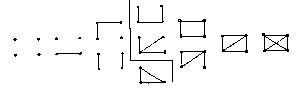
Прежде чем дать определение графа, мы покажем на рис всё 11 графов с четырьмя вершинами. Позже мы увидим, что:

1) любой граф с четырьмя вершинами изоморфен одному из них;

2) пять графов, которые на рисунке расположены слева от штриховой линии, не связны;

3) шесть графов, расположенные справа от штриховой линии, связаны;

4) последний граф — полный;

5) первый граф — пустой или вполне несвязный;

6) первый граф с четырьмя ребрами — цикл;

7) первый граф с тремя ребрами — простая цепь. Вместо того чтобы продолжать

повествование на интуитивном уровне, вводя время от времени, различные понятия теории графов, мы перейдем к систематическому, хотя и утомительному, введению этих понятий одного за другим. Граф G состоит из конечного непустого множества V, содержащего р вершин, и заданного множества X, содержащего q неупорядоченных пар различных вершин из V.

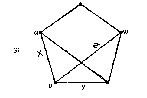
Каждую пару x= {и, v} вершин в X называютребромграфа G

и говорят, что xсоединяетuиv. Мы будем писатьx=uv и говорить, чтоuиv-смежные вершиныиногда это обозначается uadj v; вершинаuи ребро хинцидентнытак же как v иx. Если два различных ребраxиyинцидентны одной и той же вершине, то они называютсясмежными. Граф с р вершинами и q ребрами называется (р, q)-графом. (1,0)-граф называетсятривиальным.

Обычно граф представляется диаграммой, и ее-то часто называют графом. Таким образом, у графа G на рисунке вершины uиvсмежные, а вершиныuи w нет; ребраxиyсмежные, аxиzнет. Хотя на диаграмме ребра x иyпересекаются, их точка пересечения не является вершиной графа.

Имеется несколько типов графов, которые целесообразно привести. Отметим, что из определения вытекает, что в графе не может быть петель, т. е. ребер, соединяющих вершины сами с собой. Вмультиграфене допускаются петли, но пары вершин могут соединяться более чем одним ребром; эти ребра называютсякратными. Если допускаются петли и кратные ребра, получаемпсевдограф.

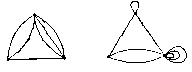
На рис. приведены мультиграф и псевдограф, в основе которых «лежит» один и тот же граф - треугольник.

Ориентированныйграф, илиорграф, D состоит из конечного непустого множества V вершин и заданного набора X упорядоченных пар различных вершин. Элементы из X называютсяориентированными ребрами, илидугами. По определению в орграфе нет

петель и кратных дуг. Направленныйграф — это орграф, не имеющий симметричных пар ориентированных ребер. На рисунке приведены все орграфы с тремя вершинами и тремя дугами; два последних из них — направленные графы.

Граф называется помеченным.(илиперенумерованным), если его вершины отличаются одна от другой какими-либо пометками, например v1, ... , vn. Графы G1 и G2 на рисунке помеченные, а граф G3 нет.

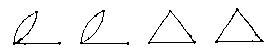
Два графа G и Н изоморфны(записывается GH или иногда G=H), если между их множествами вершин существует взаимно однозначное соответствие, сохраняющее смежность. Например, G1 и G2 на изоморфны при соответствии ui <--> vi и чисто случайно оказалось, что граф G3 изоморфен каждому из них. Совершенно очевидно, что изоморфизм есть отношение эквивалентности на графах.

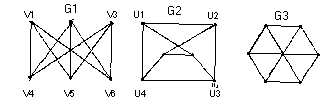
Инвариант графа G — это число, связанное с G, которое принимает одно и то же значение на любом графе, изоморфном G. Так, числа р и q являются инвариантами графа. Полный набор инвариантовопределяет граф с точностью до изоморфизма Например, числа р и q образуют полный набор инвариантов для всех графов с числом вершин, меньшим четырех. В настоящее время мы не знаем ни одной полной нетривиальной системы инвариантов для графов.

Подграфом графа G называется граф, у которого все вершины и ребра принадлежат G. Если d— подграф графа G, то G называетсянадграфом(supergraph) графа d.Остовный подграф — это подграф графа G, содержащий все его вершины. Для любого подмножества S вершин графа Gпорожденным подграфом<S> называется максимальный подграф графа G, множеством вершин которого является S. Таким образом, две вершины из S смежны в <S> тогда и только тогда, когда они смежны в G. На рисунке G2— остовный подграф графа G1, а G2 нет; G1 - порожденный подграф, а G2 нет.

Удаление вершиныu,- из графа G приводит к подграфу G - vi, содержащему все вершины графа G, за исключением vi, и все ребра графа G, не инцидентные vi. Другими словами, G - vi есть максимальный подграф графа G, не содержащий vi.Удаление ребраxj из G приводит к остовному подграфу, содержащему все ребра графа G, за исключениемxj, т. е. G -xj есть максимальный подграф графа G,

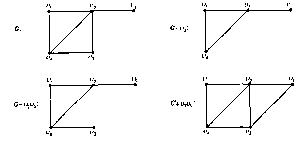
не содержащий xj. Удаление произвольного множества вершин или ребер из G определяется как последовательное удаление всех элементов этого множества. С другой стороны, если vi иui не смежны в G, тодобавление ребраviui образует наименьший надграф графа G, содержащий ребро viui . Эти понятия иллюстрируются на рисунке.

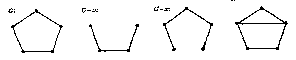
Существуют графы, для которых результат удаления вершины или ребра или же добавления ребра не зависит от выбора вершины или ребра. Для графа G, обладающего этим свойством, обозначим соответствующие графы через G - u, G -xи G+x;

Улам [1] высказал предположение, что набор подграфов G—vi несет полную информацию о всем графе G.

Гипотеза Улама.Пусть граф G имеет р вершин и, граф Н имеет р вершин ui и р>= 3. Если для каждого i подграфы Gi = G - vi и Н = Н - ui изоморфны, то и графы G и Н изоморфны.

Нарисуем каждый из р непомеченных графов G-u, на карточке размером 3x5. В гипотезе говорится, что любой граф с р вершинами, из которого, удаляя каждый раз лишь по одной вершине, можно получить данные подграфы и только их, изоморфен G. Таким образом, в гипотезе Улама утверждается, что любые два графа с одним и тем же набором карточек изоморфны. Кажется, более естественным пытаться доказать (или опровергнуть), что по любому допустимому набору карточек восстанавливается только один граф.