
- •III. Ряды
- •1.2. Ряды с неотрицательными членами
- •Найти все значения , при которых сходится ряд :
- •Исследовать на сходимость ряд с помощью признака Даламбера:
- •Исследовать на сходимость ряд с помощью признака Коши:
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§ 2. Функциональные ряды
- •2.1. Признаки сходимости функциональных рядов
- •Свойства функциональных рядов
- •2.2. Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение основных элементарных функций в ряд Маклорена
- •§ 3. Тригонометрические ряды Фурье
Найти все значения , при которых сходится ряд :
|
1.53.
|
1.54.
| |
|
1.55.
|
| |
|
1.56.
|
| |
Исследовать на сходимость ряд с помощью признака Даламбера:
|
1.57.
|
1.58.
|
|
1.59.
|
1.60.
|
|
1.61.
|
1.62.
|
|
1.63.
|
1.64.
|
|
1.65.
|
1.66.
|
Исследовать на сходимость ряд с помощью признака Коши:
|
1.67.
|
1.68.
|
|
1.69.
|
1.70.
|
|
1.71.
|
1.72.
|
|
1.73.
|
1.74.
|
Исследовать на
сходимость ряд
![]() с помощью признака Раабе или признака
Гаусса:
с помощью признака Раабе или признака
Гаусса:
|
1.75.
|
1.76.
| |
|
1.77.
|
1.78.
| |
|
1.79.
|
| |
|
1.80.
|
| |
Исследовать на
сходимость ряд
![]() :
:
|
1.81.
|
1.82.
|
|
1.83.
|
1.84.
|
|
1.85.
|
1.86.
|
|
1.87.
|
1.88.
|
|
1.89.
|
1.90.
|
Ответы: 1.33.
Сходится. 1.34.
Расходится.
1.35.
Сходится. 1.36.
Сходится. 1.37.
Сходится. 1.38.
Расходится. 1.39.
Сходится. 1.40.
Расходится. 1.41. Расходится.
1.42.
Сходится. 1.43.
Сходится. 1.44.
Сходится. 1.45.
Сходится. 1.46.
Сходится. 1.47.
Сходится. 1.48.
Расходится. 1.49.
Расходится. 1.50.
Сходится. 1.51.
Сходится. 1.52.
Сходится. 1.53.
![]() .1.54.
.1.54.
![]() .1.55.
.1.55. ![]() .1.56.
.1.56.
![]() .1.57.
Сходится. 1.58.
Сходится при
.1.57.
Сходится. 1.58.
Сходится при
![]() ,
расходится при
,
расходится при![]() .1.59.
Признак Даламбера не решает вопроса о
сходимости данного ряда. 1.60.
Расходится. 1.61.
Сходится. 1.62.
Сходится. 1.63.
Сходится. 1.64. Сходится.
1.65.
Сходится. 1.66.
Сходится. 1.67.
Сходится. 1.68.
Сходится. 1.69.
Расходится. 1.70.
Сходится. 1.71.
Сходится. 1.72.
Сходится. 1.73. Сходится.
1.74.
Сходится. 1.75.
Сходится при
.1.59.
Признак Даламбера не решает вопроса о
сходимости данного ряда. 1.60.
Расходится. 1.61.
Сходится. 1.62.
Сходится. 1.63.
Сходится. 1.64. Сходится.
1.65.
Сходится. 1.66.
Сходится. 1.67.
Сходится. 1.68.
Сходится. 1.69.
Расходится. 1.70.
Сходится. 1.71.
Сходится. 1.72.
Сходится. 1.73. Сходится.
1.74.
Сходится. 1.75.
Сходится при
![]() .1.76.
Сходится, если
.1.76.
Сходится, если
![]() ,
и расходится, если
,
и расходится, если![]() .1.77.
Сходится, если
.1.77.
Сходится, если
![]() ,
и расходится, если
,
и расходится, если![]() .1.78.
Сходится при
.1.78.
Сходится при
![]() .1.79.
Сходится. 1.80.
Сходится при
.1.79.
Сходится. 1.80.
Сходится при
![]() .1.81.
Сходится. 1.82.
Сходится. 1.83.
Сходится. 1.84.
Сходится при
.1.81.
Сходится. 1.82.
Сходится. 1.83.
Сходится. 1.84.
Сходится при
![]()
![]() и при
и при![]() ,
если
,
если![]() .1.85.
Сходится. 1.86.
Сходится. 1.87.
Сходится. 1.88.
Расходится.
1.89.
Сходится. 1.90.
Сходится.
.1.85.
Сходится. 1.86.
Сходится. 1.87.
Сходится. 1.88.
Расходится.
1.89.
Сходится. 1.90.
Сходится.
1.3. Знакопеременные ряды. Абсолютная и условная сходимость
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Ряд
 ,
где
,
где![]() ,
называетсязнакочередующимся,
или альтернирующим.
,
называетсязнакочередующимся,
или альтернирующим.
Абсолютно
сходящимся рядом
называется сходящийся ряд
![]() ,
для которого сходится и ряд
,
для которого сходится и ряд![]() .
.
Свойства абсолютно сходящихся рядов таковы.
1. Абсолютно
сходящийся ряд сходится, т. е. из сходимости
ряда
![]() следует сходимость ряда
следует сходимость ряда![]() .
.
Если ряды
 и
и абсолютно сходятся, то при любых
абсолютно сходятся, то при любых и
и ряд
ряд также абсолютно сходится.
также абсолютно сходится.Если ряд абсолютно сходится, то ряд, составленный из тех же членов, но взятых в другом порядке, также абсолютно сходится, и его сумма равна сумме исходного ряда.
4. Правило
Коши. Если
ряды
![]() и
и![]() абсолютно сходятся, то
абсолютно сходятся, то
 ,
,
где
![]() .
.
Ряд
![]() также абсолютно сходится, а его сумма
равна
также абсолютно сходится, а его сумма
равна![]() ,
где
,
где![]() и
и![]() – суммы рядов
– суммы рядов![]() и
и![]() .
.
Если ряд
![]() сходится, а ряд
сходится, а ряд![]() расходится, то такой ряд называетсяусловно
сходящимся.
расходится, то такой ряд называетсяусловно
сходящимся.
Если один из рядов
![]() или
или![]() сходится условно, а второй – абсолютно,
то для их произведения справедливо
правило Коши.
сходится условно, а второй – абсолютно,
то для их произведения справедливо
правило Коши.
Теорема Римана.
Если ряд
![]() сходится условно, то каким бы ни было
число
сходится условно, то каким бы ни было
число![]() ,
можно так переставить члены ряда, что
сумма полученного ряда будет равна
,
можно так переставить члены ряда, что
сумма полученного ряда будет равна![]() .
.
Признак
сходимости Лейбница. Пусть
для ряда
 выполнены
условия:
выполнены
условия:
1.
![]() ; 2.
; 2.![]() .
.
Тогда этот ряд
сходится и его сумма удовлетворяет
неравенству
![]() .
.
Для остатка
альтернирующего ряда
![]() справедливо неравенство
справедливо неравенство![]() .
Таким образом,модуль
остатка не превосходит модуля первого
из отбрасываемых членов.
.
Таким образом,модуль
остатка не превосходит модуля первого
из отбрасываемых членов.
Признак Абеля.
Если ряд
![]() сходится, а числа
сходится, а числа![]() образуют монотонную и ограниченную
последовательность, то ряд
образуют монотонную и ограниченную
последовательность, то ряд сходится.
сходится.
Признак Дирихле.
Если частичные суммы ряда
![]() ограничены в совокупности (т. е.
ограничены в совокупности (т. е.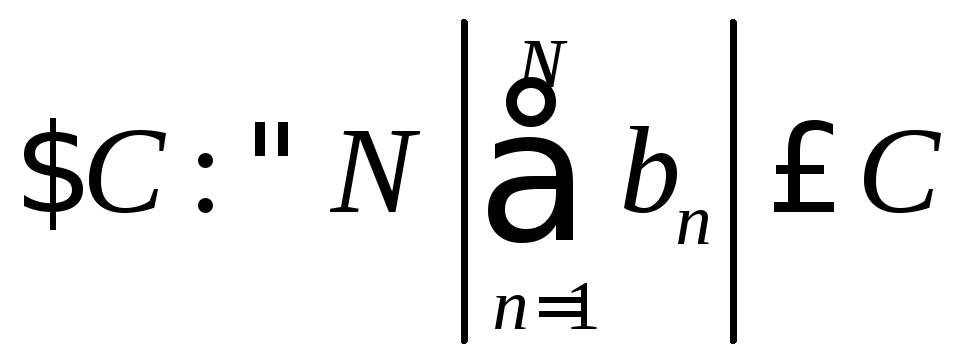 ),
а последовательность
),
а последовательность![]() монотонно стремится к нулю, то ряд
монотонно стремится к нулю, то ряд сходится.
сходится.
Следствие
признака Дирихле.
Если последовательность
![]() моно-
моно-
тонно стремится
к нулю, то ряд
 сходится при любом
сходится при любом![]() ,
а ряд
,
а ряд
 сходится при
сходится при
![]() .
.
Пример 1.6.
Исследовать
на сходимость ряд
 .
.
Решение. Это знакочередующийся ряд. Проверим выполнение условий признака Лейбница.
Рассмотрим функцию
 .
Тогда
.
Тогда ,
,
 ,
если
,
если .
Значит, при
.
Значит, при функция
функция монотонно убывает.
монотонно убывает. .
.
Ряд сходится.
Пример 1.7. Исследовать на сходимость и абсолютную сходимость ряды:
а)
 ; б)
; б)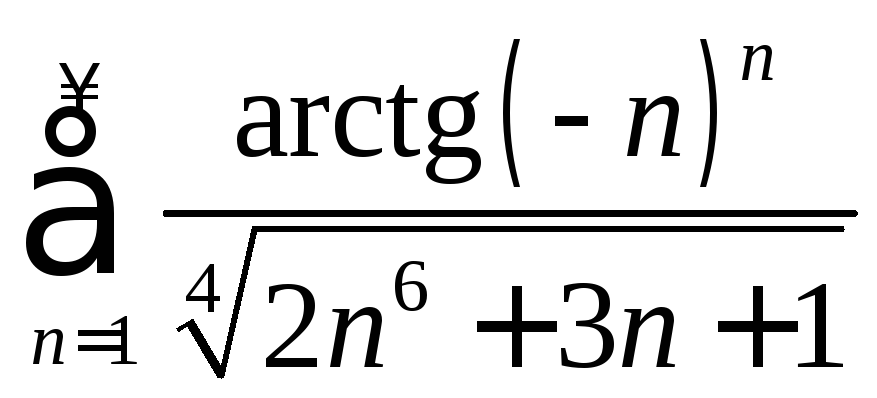 ; в)
; в) .
.
Решение. а)
Используя неравенства
![]() ,
,![]() ,
получаем
,
получаем .
Из сходимости ряда
.
Из сходимости ряда по признаку сравнения следует сходимость
ряда
по признаку сравнения следует сходимость
ряда![]() ,
т. е. абсолютная сходимость ряда
,
т. е. абсолютная сходимость ряда![]() .
.
б) Используя
неравенства
![]() ,
,![]() ,
получаем
,
получаем .
Из сходимости ряда
.
Из сходимости ряда по признаку сравнения следует сходимость
ряда
по признаку сравнения следует сходимость
ряда![]() ,
т. е. абсолютная сходимость ряда
,
т. е. абсолютная сходимость ряда![]() .
.
в) Используя
неравенство
![]() ,
получаем
,
получаем .
Ряд
.
Ряд расходится, т. к.
расходится, т. к.

 и
ряд
и
ряд![]() расходится, а ряд
расходится, а ряд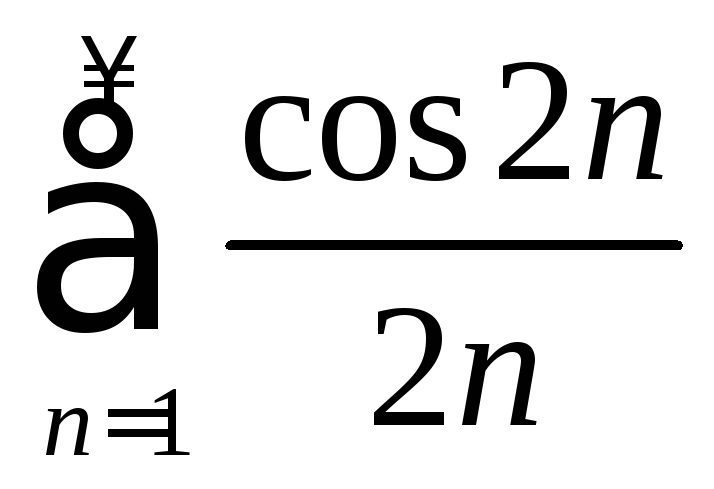 сходится. Проверим условную сходимость.
Последовательность
сходится. Проверим условную сходимость.
Последовательность![]() монотонно стремится к нулю; следовательно,
ряд
монотонно стремится к нулю; следовательно,
ряд сходится. Ряд
сходится. Ряд сходится условно.
сходится условно.
Доказать, что ряды абсолютно сходятся:
|
1.91.
|
1.92.
|
|
1.93.
|
1.94.
|
Исследовать на сходимость ряды:
|
1.95.
|
1.96.
|
|
1.97.
|
1.98.
|
Исследовать на сходимость и абсолютную сходимость ряды:
|
1.99.
|
1.100.
|
|
1.101.
|
|
Исследовать на сходимость ряды:
|
1.102.
|
1.103.
|
|
1.104.
|
|
Найти все значения
![]() ,
при которых ряд: а) абсолютно сходится;
б) условно
сходится:
,
при которых ряд: а) абсолютно сходится;
б) условно
сходится:
|
1.105.
|
1.106.
| |
|
1.107.
|
1.108.
| |
|
1.109.
|
1.110.
| |
|
1.111.
|
1.112.
| |
|
1.113.
|
| |
|
1.114.
|
| |
Найти все значения
![]() и
и![]() ,
при которых ряд: а) абсолютно сходится;
б) условно сходится:
,
при которых ряд: а) абсолютно сходится;
б) условно сходится:
|
1.115.
|
|
|
1.116.
|
|
|
1.117.
|
|
1.118. Пользуясь одним из равенств
![]() ,
,
![]() ,
,
где
![]() ,
доказать, что
,
доказать, что .
.
Пользуясь тем, что
 ,
найти суммы следующих рядов, полученных
из данного перестановкой его членов:
,
найти суммы следующих рядов, полученных
из данного перестановкой его членов:
|
1.119.
|
|
|
1.120.
|
|
|
1.121.
|
|
1.122. Пусть
ряд
![]() сходится и
сходится и .
Следует ли отсюда, что ряд
.
Следует ли отсюда, что ряд![]() также сходится?
также сходится?
Ответы: 1.95.
Сходится. 1.96.
Сходится. 1.97.
Сходится. 1.98.
Сходится. 1.99. Сходится
условно. 1.100.
Сходится абсолютно. 1.101.
Сходится условно. 1.102.
Сходится. 1.103.
Расходится. 1.104.
Расходится. 1.105.
а) ![]() ;
б)
;
б)![]() .1.106.
а)
.1.106.
а)
![]() ;
б)
;
б)![]() .1.107.
а)
.1.107.
а)
![]() ;
б)
;
б)![]() .1.108. а)
.1.108. а) ![]() ;
б)
;
б)![]() .1.109.
а)
.1.109.
а)
![]() ;
б)
;
б)![]() .1.110.
а)
.1.110.
а)
![]() ;
б)
;
б) ![]() любое.
1.111.
а)
любое.
1.111.
а)
![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() .1.112. а)
.1.112. а) ![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() .1.113. а)
.1.113. а)
![]() ;
б)
;
б)![]() .1.114.
а)
.1.114.
а)
![]() ;
б)
;
б)![]() .1.115.
а)
.1.115.
а)
![]() ;
б)
;
б) ![]() .1.116.
а)
.1.116.
а)
![]() ,
,![]() ;
б)
;
б)![]() .1.117.
а)
.1.117.
а)
![]() ,
,![]() ;
б)
;
б) ![]() .1.119.
.1.119.
![]() .1.120.
.1.120.
![]() .1.121.
0. 1.122.
Нет. Пример:
.1.121.
0. 1.122.
Нет. Пример:
![]() ,
,![]() .
.

 .
. .
. .
. ,
,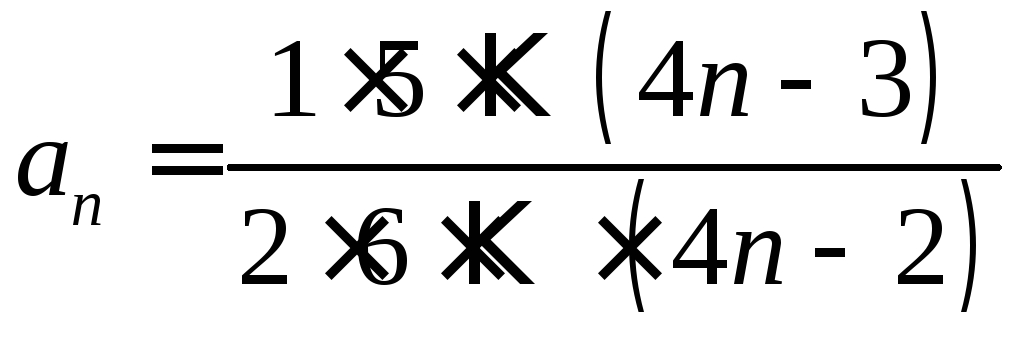 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.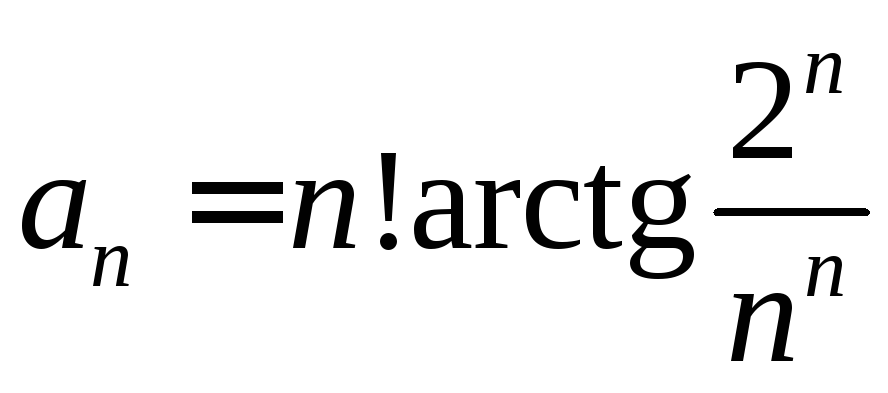 .
. .
. .
.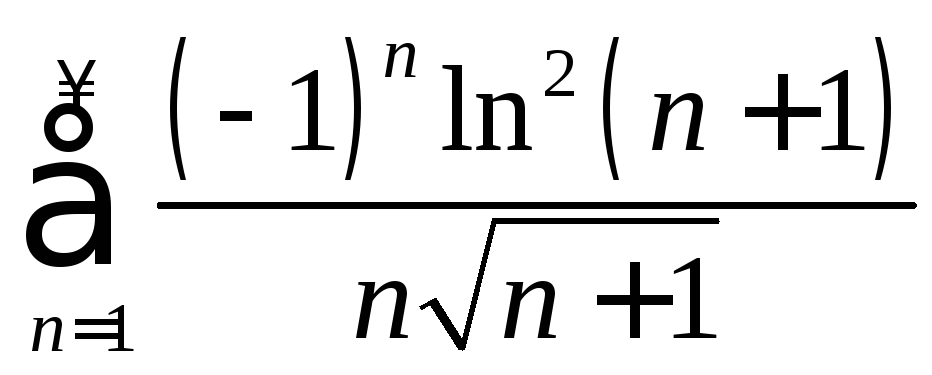 .
. .
. .
. .
. .
. .
. .
. .
.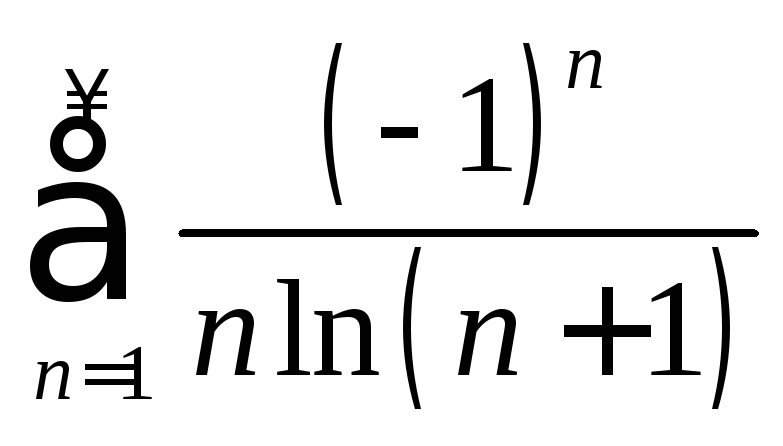 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.