Levitskiy_chm3-1

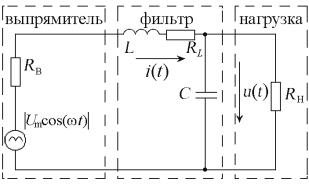
61

Задание 11. Напряжение с выхода двухполупериодного диодного выпрямителя подается на нагрузку через LC-фильтр, ослабляющий нежелательные пульсации. Зависимости напряжения u на выходе фильтра и общий ток i в цепи от времени t описываются системой дифференциальных уравнений

1

u

du

=

i −

,

C

dt

RH

di

1

Um cos(ωt )

=

−iR0 −u ,

dt

L

где L и C – индуктивность дросселя

и

емкость

конденсатора

фильтра,

RН

–

сопротивление

нагрузки,

R0 = RВ + RL, RВ – выходное сопро-

тивление выпрямителя, RL – сопротивление обмотки дросселя, Um – амплитуда пульсирующего напряжения на выходе выпрямителя, ω = 2π f – угловая частота.

Рассчитайте и постройте графики зависимостей uВ(t) = |Umcos(ωt)|,

	u(t) и i(t). Исходные данные: Um = 12 В и f = 50 Гц. Начальные условия
	u(t = 0) = 0,	i(t = 0) = 0. Параметры R0, RН, L и C приведены в таблице.
	Параметр			В а р и а н т
		11-1	11-2	11-3	11-4	11-5	11-6
	R0, Ом	20	75	35	120	90	20
	RН, Ом	500	1000	750	1000	2000	1000
	L, Гн	0,5	0,7	0,1	1	1,2	0,05
	C, мкФ	100	40	200	50	100	1000

Задача 12. Уравнение Ван-дер-Поля, описывающее колебания в нелинейной системе (например, автогенераторе), имеет следующий вид:

y′′ + (y2 −b) y′ + y = 0 ,

где y, y' и y" – функция, её первая и вторая производные по времени t. Постоянная b определяет потери в системе. Нелинейные свойства системы, например рабочие характеристики активного элемента генератора, учитываются слагаемым y2.

Задавшись указанными в таблице начальными условиями и параметром b, решите уравнение и постройте графики зависимостей y(t) и y'(t), охватывающие несколько периодов колебаний.

	Параметр			В а р и а н т
		12-1	12-2	12-3	12-4	12-5	12-6
	y(0)	1	0	1	2	2	-3
	y'(0)	1	1	-2	1	3	20
	b	7	3 y	y	y'	1,5 y'	0

62

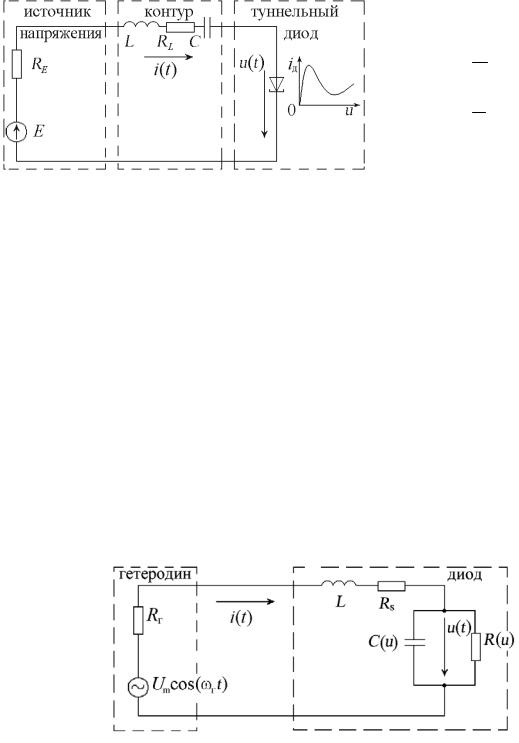
Задание 13. Генератор, выполненный на туннельном диоде, содержит последовательный электрический LC-контур и источник постоянного напряжения E. Колебания напряжения u(t) и тока i(t) в генераторе описываются системой дифференциаль-

ных уравнений

dudt = C1 i −iд (u) ,

dudt = L1 [E −iR0 −u],

где t – время, L и C – индуктивность катушки и емкость конденсатора контура, R0 = RE + RL, RE – внутреннее сопротивление источни-

ка питания, RL – сопротивление обмотки катушки индуктивности. N-образная вольт-амперная характеристика туннельного диода iД(u)

описывается формулой

iД (u) = (0,6u −14u3 + 20u4 )exp(−10u)+ 0,02 exp(u)−1 .

Рассчитайте и постройте графики зависимостей u(t) и i(t). Начальные условия u(t = 0) = 0, i(t = 0) = 0. Параметры E, R0, L и C даны в таблице.

	Параметр			В а р и а н т
		13-1	13-2	13-3	13-4	13-5	13-6
	E, В	0,27	0,3	0,22	0,18	0,36	0,19
	R0, Ом	7	4,2	3,5	4,8	11,3	5,2
	L, нГн	20	7·103	1,5·104	10	17	200
	C, пФ	12	2200	130	12	27	120

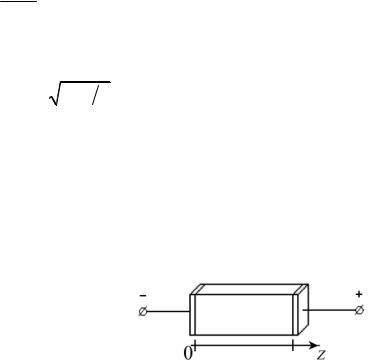
Задание 14. При расчете преобразователя частоты на диоде с барьером Шоттки используется эквивалентная схема, показанная на рисунке.

Элементы Umcos(ωГt) и Rг на рисунке относятся к гетеродину, напряжение с которого поступает на смесительный диод. Диод представлен эквивалентной схемой, содержащей следующие элементы: L – индуктивность выводов, RS – омическое сопротивление потерь, C(u) и R(u) – емкость и сопротивление

63

барьерной области диода, зависящие от обратного смещения на его переходе. Зависимости напряжения u на барьере диода и тока i в общей цепи от времени t могут быть найдены из нелинейной системы дифференциальных уравнений

1

u

du

=

i −

,

C(u)

R(u)

dt

di

=

1

U

cos

ω t

)

−u −i

(

R + R

.

L

m

( г

s г )

dt

данных: Rг = 50 Ом,

Решите систему

уравнений

при

следующих

L = 1,2 нГн, Rs = 6 Ом. Начальные условия: u(t) = 0, i(t) = 0 при t = 0. Амплитуда Um и частота fг колебаний гетеродина указаны в таблице.

	Параметр			В а р и а н т
		14-1	14-2	14-3	14-4	14-5	14-6
	L, нГн	1,2	1,5	1,7	1,4	2,2	1,1
	RS, Ом	6	5,5	4,7	5,8	4,8	7
	Um, В	0,65	0,55	0,7	0,8	0,9	0,97
	fг, ГГц	9	14	11	8,2	12	16

В расчете применяйте следующие аппроксимации зависимостей R(u) и С(u) для диода с барьером Шоттки. Для вольт-амперной характеристики используйте формулу

iд(u) = Ru(u) =i0 [exp(bu) −1],

где i0 = 5 ·10–13 А, b = 28 1/В. Зависимость С(u) описывается формулой

C(u) =	C0	,
	1−u ϕ

где C0 = 0,14 пФ, ϕ = 0,85 В – высота потенциального барьера.

Рассчитайте несколько периодов колебаний и постройте графики зави-

симостей uГ(t) = Umcos(ωГt), u(t) и i(t).

Задание 15. Распределение напряженности электрического поля в полупроводнике описывается уравнением Пуассона. Для одномерного случая, когда изменение поля рассматривается только по координате z (вдоль полупроводникового образца), это уравнение можно привести к следующему виду:

dE	=	1		j	− qN		,
dz						0
		ε1
			v

где ε1 – диэлектрическая (решеточная) проницаемость полупроводника, j – плотность тока вдоль оси 0z, v – дрейфовая скорость электронов вдоль оси 0z, q = 1,6·10–19 Кл – элементарный заряд, N0 – уровень легирования полупроводника.

64

В полупроводнике типа арсенида галлия зависимость дрейфовой скорости v от напряженности электрического поля E существенно нелинейная.

Характеристика v(E) описывается аппроксимацией:

v(E)=	µ	E + v	(E E	)4
	0	S	t		,
		1+ (E Et )4

где µ0 = 0,6 м2/В с, vS = 105 м/с, Еt = 3,5·105 В/м.

Решите уравнение при следующих данных: диэлектрическая проницаемость ε1 = 12,5ε0 = 12,5 × 8,85·10–12 Ф/м, поперечное сечение образца S = 2,5 мкм × 300 мкм. Ток i = j S, протекающий через образец, и начальное значение E(z) при z = 0 указаны в таблице.

Рассчитайте зависимость E(z) на участке структуры длиной не менее 50 мкм и найдите соответствующее распределение концентрации свободных

носителей заряда n(z)= j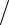qv E (z) .

Параметр			В а р и а н т
	15-1	15-2	15-3	15-4	15-5	15-6
N0, м–3	5·1020	4,5·1020	5,3·1020	4·1020	5,7·1020	4,1·1020
i, мА	5,5	8,3	6,7	7,45	10,6	7,62
E(0), В/м	0,1·105	3,7·105	2,5·105	3·105	3,5·105	3,6·105

Задание 16. Для охлаждения микропроцессора используется металлический теплоотводящий радиатор. Процесс передачи тепла от радиатора в окружающий воздух описывается дифференциальным уравнением

cm dTdt = P − αS (T −TC ) ,

где m и c – масса и удельная теплоемкость материала радиатора, T – температура радиатора, t – время, P – выделяемая микропроцессором мощность, αS (T −TC ) – отводимое тепло, α – коэффициент теплоотдачи конвекцией,

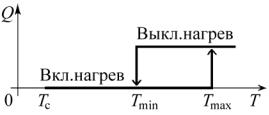
S – площадь поверхности радиатора, ТС – температура окружающей среды. Радиатор снабжен вентилятором, который автоматически включается

если температура процессора и радиатора превышает допустимый предел, то есть Т > Тmax, и останавливается, если Т < Тmin. Включение обдува эквивалентно изменению коэффициента теплоотдачи α по следующему закону:

α= α0, еслиT ≤Tmin илиT <Tmax приdT/dt >0,α1, еслиT ≥Tmax илиT >Tmin приdT/dt <0,

где α0 – коэффициент теплоотдачи при выключенном вентиляторе, α1 – коэффициент теплоотдачи при обдуве.

65

Рассчитайте участок зависимости Т(t), на котором система охлаждения выходит на рабочий режим Tmin < Т(t) < Tmax. Параметры радиатора: c = 950 Дж/кг·К, m = 0,05 кг, S = 0,04 м2. Начальную температуру процессора примите равной Т(t=0) = Тc = 293 K. Прочие данные указаны в таблице.

Параметр			В а р и а н т
	16-1	16-2	16-3	16-4	16-5	16-6
P, Вт	42	55	27	65	43	22
α0, Вт/м2·K	17	15	12	25	21	9
α1, Вт/м2·K	80	95	35	82	160	75
Тmin, K	313	308	313	313	308	303
Тmax, K	353	343	343	353	343	343

Задание 17. Работа системы автоматического регулирования температуры нагревателя описывается дифференциальным уравнением

cm dTdt = Qвх −αS (T −Tc ) ,

где c и m – удельная теплоемкость и масса нагревателя, T – температура нагревателя, t – время, Qвх – вырабатываемое нагревателем тепло, α – приведенный коэффициент теплоотдачи, S – площадь поверхности нагревателя,

Тс – температура окружающей среды.

Для поддержания температуры T заданных пределах Tmin < T < Tmax нагреватель мощностью P переключается по следующему закону:

Q = P, еслиT ≤Tmin илиT <Tmax приdT/dt >0,

вх 0, еслиT ≥Tmax илиT >Tmin приdT/dt <0,

где Тmin и Тmax – минимальное и максимальное значения температуры.

Рассчитайте участок зависимости Т(t), на котором нагреватель выходит

на рабочий режим при начальной его температуре Т(t=0) = Тc и Tmin = 290 К, Tmax = 295 К. Мощность P и другие параметры даны в таблице.

Параметр			В а р и а н т
	17-1	17-2	17-3	17-4	17-5	17-6
P, Вт	2000	250	350	1000	750	500
cm, Дж/К	240	140	100	270	700	470
α	15	5	8	10	5	7
S, Вт/K
Τс, K	288	263	275	233	278	293
Τmin, K	290	290	300	290	313	303
Τmax, K	295	305	315	325	328	333

66

Задание 18. Для защиты электрических цепей от перегрузки используются плавкие предохранители. Процесс нагрева плавкого элемента до его разрушения описывается уравнением теплового баланса

(

c m + c m

dT + αS

(

T −T

= i2 R

1+β

(

T −T ,

1 1 2 2 )

dt

C )

0

0 )

c1

и m1 –

где

удельная

теплоемкость

и масса

плавкого элемента,

c2 и m2 –

удельная теплоемкость и масса среды, в которой находится элемент,

T

–

температура

элемента, t – время, α – коэффициент теплоотдачи,

S

–

поверхность

охлаждения, TC

– температура

окружающей среды,

i – ток, протекающий через элемент, R0 – электрическое сопротивление элемента при T0 = 293 K, β – температурный коэффициент сопротивления.

Эффективность защиты зависит от того, насколько быстро при перегрузке плавкий элемент предохранителя разорвет электрическую цепь.

Рассчитайте зависимость T(t) при начальном условии T(t=0) = TC = 293 K. Слагаемое c2m2 в уравнении полагайте равным нулю. Определите время, за которое перегорает предохранитель, если температура плавления его рабочего элемента равна 1373 K.

	Параметр			В а р и а н т
		18-1	18-2	18-3	18-4	18-5	18-6
	c1m1, Дж/K	1,7·10–4	5·10–4	3,3·10–4	4,4·10–5	8·10–4	1,4·10–3
	αS, Вт/K	3·10–5	3,5·10–5	4·10–5	1,2·10–5	6·10–5	7·10–5
	R0, Ом	0,04	0,014	0,017	0,14	0,006	0,004
	i, А	1	2	1,5	0,5	3	5
	β, 1/K	0,05	0,06	0,05	0,04	0,07	0,08

Задание 19. Движение снаряда, выпущенного под углом θ к горизонту (см. рисунок), описывается системой дифференциальных уравнений, являющихся уравнениями баланса сил, действующих вдоль координат x и y:

		d 2x		= −kvx ,
	m		2
		dt
		d 2 y		= −kvy − gm ,
	m	dt	2

где vx = v cosθ и vy = v cosθ – горизонтальная и вертикальная составляющая скорости снаряда v = vx2 + vy2 , t – время, k – коэффициент трения, учиты-

вающий сопротивление воздуха, m – масса снаряда, g ≈ 9,8 м/c2 – ускорение свободного падения.

С учетом vx = dx/dt и vy = dy/dt исходная система уравнений приводится к следующему виду:

			67
dx dt			= vx ,
		dt = −k m vx ,
dvx
		dt	= vy ,
dy
dv	y	dt = −k m v		y	− g.

Рассчитайте зависимости x(t) и y(t). Постройте траекторию снаряда y(x) из точки x(t=0) = 0 и y(t=0) = 0 при заданных k, m, θ и начальной скорости v(t=0).

Параметр							В а р и а н т
	19-1		19-2				19-3		19-4	19-5	19-6
k, кг/c	1,4		0,05				2,9		1	2	1,8
m, кг	15		0,3				110		42	85	52
v(t=0), м/с	300		10				350		140	300	330
θ, град	15		45				25		33	20	45
Задание 20. Процесс производства, хранения и сбыта товара описыва-
ется системой дифференциальных уравнений
		dT		= O	− k T (S −V ) ,
		dt			1
		dV		= k1T (S			−V ) − k2V ,
		dt
		dD = Ck T (S −V ) − O − k T ,
					1		C		3
		dt

где T – количество товара на рынке, V – количество не потребленного товара у покупателей, D – доход в единицу времени, O – объем выпуска товара, k1 – коэффициент скорости продаж, S – потенциальный спрос (объем товара, удовлетворяющий потребность при отсутствии ажиотажного спроса), C – условная цена товара (C > 1), k2 – коэффициент потребления товара, k3 – плата за хранение единицы товара. Переменные T, O, V, D и параметры S и C измеряются в условных денежных единицах.

Рассчитайте зависимости T(t), V(t) и D(t) при начальном условии D(t=0) = 0. Остальные данные приведены в таблице.

	Параметр			В а р и а н т
		20-1	20-2	20-3	20-4	20-5	20-6
	T(t=0)	3	10	15	4	12	7
	V(t=0)	3	20	5	11	12	5
	O	11,7	7	21	15	18	32,6
	S	15,5	3	18	15	21	18
	C	1,2	1,3	1,5	1,1	1,2	1,2
	k1	0,02	0,03	0,2	0,5	0,05	0,02
	k2	3	2	1,1	2	1,3	2,6
	k3	0,01	0,001	0,1	0,05	0,12	0,04

68

Лабораторная работа № 3 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

ВЧАСТНЫХ ПРОИЗВОДНЫХ

1.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Большое число задач, связанных с анализом физических (и не только физических) полей описываются дифференциальными уравнениями в частных производных. К сожалению, во многих случаях, представляющих практический интерес, найти аналитическое решение таких задач трудно или практически невозможно. Это обычно обусловлено сложной формой или неоднородностью свойств области, в которой отыскивается решение.

Однако результат можно получить численно с помощью компьютера. Подходы к решению дифференциальных уравнений с частными производными определяются их математической формой. Поэтому рассмотрим классификацию уравнений с этой точки зрения.

1.1. Классификация уравнений по математической форме

Во многих случаях для описания физических процессов используют уравнений с частными производными до второго порядка включительно.

Так, например, изучение свободных колебаний различной природы приводит к волновым уравнениям вида

2

u2

2

u2

2

u2

1

2

u2 = 0,

∂

+

∂

+

∂

−

∂

(1)

2

∂t

∂x

∂y

∂z

c

где u(x,y,z,t) – функция, описывающая волновой процесс, x, y, z – координаты, с – скорость распространения волны в данной среде, t – время. Оператор

	∂	2	2	+ ∂	2	2	+∂	2		принято обозначать значком ∆, который в этом слу-
		∂x			∂y			∂z	2

чае носит название оператора Лапласа.

Процессы распространения тепловой энергии описываются уравнением теплопроводности

ρC	∂T			2		2		2		= Q,	(2)
		− k		∂ T2	+	∂ T2	+	∂ T2
	∂t			∂x		∂y		∂z
где ρ и C – плотность			и	теплоемкость					вещества,		T – температура,

k – коэффициент теплопроводности, Q – плотность источников тепла. Анализ стационарных состояний, например, статических тепловых,

электрических, магнитных полей или деформаций при статических нагрузках проводят, используя уравнение Пуассона

				69
	∂2u	+	∂2u	+	∂	2u	= − f (x, y, z),	(3)
	∂x2		∂y2		∂z2

где u(x,y,z) – функция, описывающая статическое поле, f(x,y,z) – распределенные источники. Если f(x,y,z) = 0, то (3) обращается в уравнение Лапласа:

	∂2u	+	∂2u	+	∂2u	= 0 .	(4)
	∂x2		∂y2		∂z2

Известны и другие виды задач и соответствующие им дифференциальные уравнения в частных производных, например, уравнение диффузии или уравнение Гельмгольца.

Несмотря на различие процессов, описываемых рассмотренными уравнениями, и форм их записи, все они с математической точки зрения могут быть представлены как частные случаи обобщенной формы дифференциального уравнения второго порядка.

Рассмотрим уравнение второго порядка с двумя независимыми переменными x и y:

	A	∂2u	+ 2B	∂2u	+C	∂2u	+ D = 0,	(5)
		∂x2		∂x∂y		∂y2

где A, B, С и D – некоторые функции, зависящие в общем случае от x, y, u, ∂u/∂x и ∂u/∂y, причем A, B и С одновременно не обращаются в ноль. Дифференциальные уравнения, описывающие физические поля, могут быть нелинейными. Однако на практике многие задачи рассматриваются в линейном приближении, когда уравнение с частными производными линейно относительно неизвестной функции u и ее частных производных.

На основании того, что уравнению (5) можно поставить в соответствие

квадратичную форму Aζ 2	+ Bζ ζ	2	+ Cζ 2	= 0 , по математической природе
1	1		2

различают следующие типы квазилинейных уравнений:

1)гиперболический, если B2 − 4AC > 0 – его аналогом является волновое уравнение (1);

2)параболический, если B2 − 4 AC = 0 – его аналог уравнение теплопроводности (2);

3)эллиптический, если B2 − 4 AC < 0 – аналог уравнение Пуассона (3) или Лапласа (4).

В задачах, описываемых дифференциальными уравнениями в частных производных, другой важной составляющей помимо самого уравнения явля-

ется формулировка дополнительных условий.

Для задач с уравнениями гиперболического или параболического типа, содержащих в качестве независимой переменной время t, условия по t обычно

формулируются как начальные, описывающие исходное состояние системы. По координатам x, y и z задают граничные условия. В тепловых задачах они, например, описывают распределение температуры на границе

70

расчетной области. В задачах с уравнениями эллиптического типа, не содержащими переменную t, используют только граничные условия по координатам x, y и z, а саму задачу называют краевой.

Если краевое условие задает распределение функции u на границе, то

его принято называть условием Дирихле. Условие, определяющее производ-
G	JJJJJJJJG	G	JJJG
ную n	grad(u) ≡ n		u на границе расчетной области, называют условием
Неймана. Здесь nG			– единичная нормаль к границе. Условия, представляющие

собой комбинацию двух вышеназванных, называют смешанными.

С помощью дифференциальных уравнений формулируют и другой вид задач – задачи на собственные значения, связанные, например, с определением собственных волн (частот) колебательных систем или волноведущих структур. Однако здесь они не рассматривается.

Приведенная классификация позволяет определить общие подходы к решению дифференциальных уравнений в задачах различных по физической сути, но сходных с математической точки зрения. В настоящее время широ-

кое распространение получили метод конечных разностей и метод конеч-

ных элементов, основы которых и будут рассмотрены ниже.

1.2. Основы метода конечных разностей

Метод конечных разностей заключается в том, что дифференциальное уравнение в частных производных заменяется соответствующей ему системой алгебраических уравнений. Решение этой системы дает приближенное решение для искомой функции u(x,y,z,t).

Метод включает следующие основные этапы:

1)построение сетки, охватывающей рассматриваемую область, например, элемент конструкции какого-нибудь устройства;

2)построение на полученной сетке конечно-разностной аппроксимации, эквивалентной исходному дифференциальному уравнению и дополнительным условиям;

3)формирование на основе конечно-разностной аппроксимации системы алгебраических уравнений и ее решение.

Рассмотрим перечисленные этапы на примере двухмерных задач.

1.2.1. Построение сетки

Формирование сетки производится с учетом геометрии задачи, например, формы детали, для которой выполняется расчет. Обычно для деталей, имеющих прямоугольную форму, используют декартову систему координат и соответственно прямоугольную сетку. На рис. 1 приведен пример такой двухмерной сетки, нанесенной на прямоугольную пластину.

В методе конечных разностей применяют и другие виды сеток. Например, если исследуемая конструкция содержит элементы с осевой симметрией, используют полярную сетку.