Техническое задание

Математическое моделирование потоков вызовов, обладающих различными свойствами

Расчет интенсивности нагрузки на АТС

Расчет вероятностных характеристик коммутационной системы при обслуживании простейшего и примитивного потоков вызовов полнодоступным пучком линий с явными потерями

Определение вероятностно-временных характеристик коммутационной системы вида M/M/s

Определение параметров неполнодоступной схемы со ступенчатым включением линий

Построение двухзвенной неполнодоступной схемы с равномерным включением линий

Расчет качественных показателей четырехзвенной коммутационной системы методом вероятностных графов

Определение интенсивности нагрузки по направлениям

Содержание

Задание 1 ………………………………………...…………….…………. 4

Задание 2 ………………………………………...…………….…………. 15

Задание 3 ………………………………………...…………….…………. 18

Задание 4 ………………………………………...…………….…………. 21

Задание 5 ………………………………………...…………….…………. 24

Задание 6 ………………………………………...…………….…………. 28

Задание 7 ………………………………………...…………….…………. 33

Задание 8 ………………………………………...…………….…………. 37

Список использованных источников …………………………….....….. 40

Задание 1

Определить основные свойства и характеристики потоков вызовов со следующими законами распределения интервалов между вызовами:

- простейший поток;

- распределение Эрланга;

- распределение Вейбула;

- гамма распределение;

- распределение Паретто.

Простейший поток

Простейшим потоком называется стационарный (параметр потока, а также вероятности состояний не зависят от времени), однородный (свойства всех вызовов одинаковы), ординарный (одновременно не может поступить более одного вызова), без последействия (вероятности состояний не зависят от предыстории) поток от бесконечного числа источников с экспоненциальным распределением вероятности интервалов между вызовами.

Функция плотности вероятности интервалов между вызовами:

, (1.1)

- интенсивность простейшего потока, - время.

=7.2

Рисунок 1- Функция плотности распределения вероятности интервалов между вызовами для простейшего потока

Рисунок 2- Функция распределения вероятности интервалов между вызовами для простейшего потока

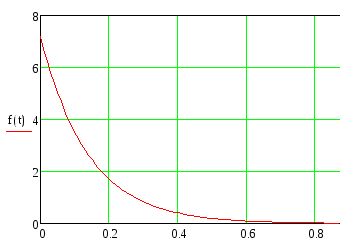
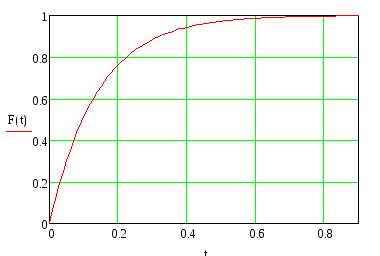
Из графиков видно, что поток является ординарным, так как в нулевой момент времени график функции распределения вероятностей имеет значение 0. Однородным, так как задается одной характеристикой, и без последействия.

Распределение Эрланга

В общем виде функция плотности распределения вероятности интервалов между вызовами имеет следующий вид:

, (1.2)

Рисунок 3 – Графики функций плотности распределения вероятности интервалов между вызовами для потока Эрланга для различных r

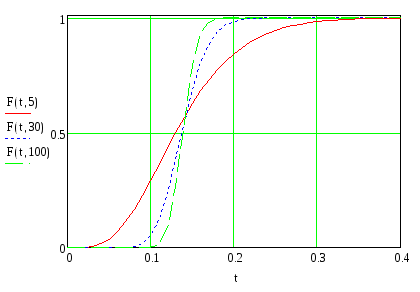
Рисунок 4 – Графики функций распределения вероятности интервалов между вызовами для потока Эрланга

Графики на рисунке 4 показывают последовательный переход распределения Эрланга из показательного (r=1) в детерминированное (при стремлении r в бесконечность).

Из вышеописанного следует, что математическое ожидание интервала между вызовами для потока Эрланга совпадает с математическим ожиданием для простейшего потока и всегда равно 1/λ. По графикам также видно, что поток является ординарным, однородным, стационарным и без последействия.

Гамма распределение

Функция плотности вероятности имеет вид:

, (1.3)

где , - Гамма функция.

Для гамма распределения параметр k лежит в пределах от нуля до бесконечности.

Построим графики функции плотности вероятности для различных значений k:

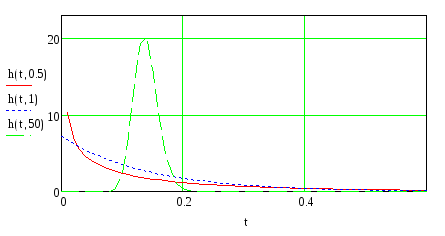
Рисунок 5 – Функции плотности распределения вероятности интервалов между вызовами для потока c Гамма - распределением для различных k

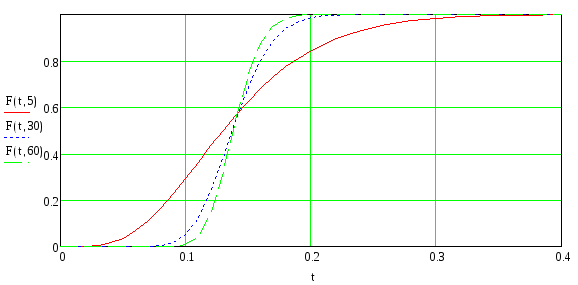
Рисунок 6 – Функции распределения вероятности интервалов между вызовами для потока c Гамма - распределением для различных k

Из графиков видно, что при k<1 гамма распределение обладает, так называемым, «тяжелым хвостом», следовательно этот поток с последействием, ординарный.

Распределение Вейбулла

Функция плотности вероятности:

, (1.4)

Рисунок 7 – Функции распределения вероятности интервалов между вызовами для потока c распределением Вейбулла

Из рисунков отчетливо видно что при k=1 распределение Вейбулла переходит

в показательное и при увеличении k стремится перейти в детерминированное,

при k<1 распределение имеет «тяжелый хвост».

Математическое ожидание распределения Вейбулла:

, (1.5)

При k=1 как и при показательном распределении. При больших k математическое ожидание также равно , а закон распределения переходит в детерминированный.

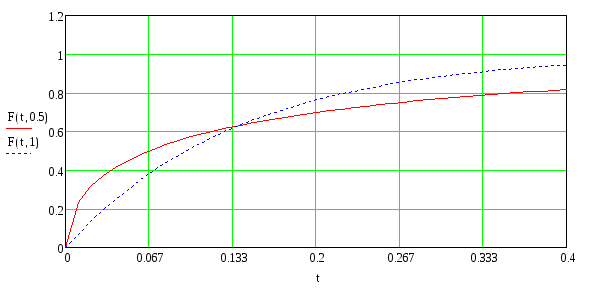Рисунок 8 – Функции распределения вероятности интервалов между вызовами для потока c распределением Вейбулла

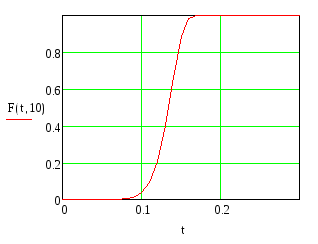
Рисунок 9 – Функции распределения вероятности интервалов между вызовами для потока c распределением Вейбулла

Поток является однородным, ординарным и с последействием, так как обладает «тяжелым хвостом».

Распределение Парето

Функция плотности вероятности имеет вид:

, (1.6)

Построим графики функции плотности вероятности при k=1 в зависимости от коэффициента самоподобия H, учитывая, что и .

Функция :

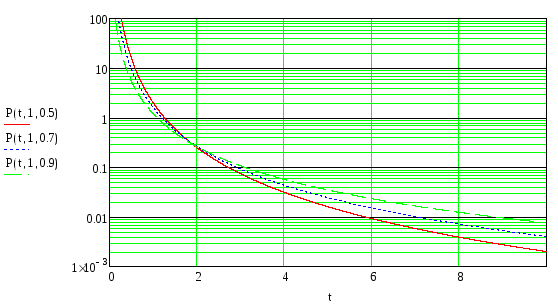
Рисунок 10 - Функции плотности вероятности для распределения Парето, при k=1, в зависимости от коэффициента подобия

Математическое ожидание:

, (1.7)

Распределение Парето обладает свойством последействия, что видно из графиков.

Сравним распределения Гама, Вейбула и Паретто при k<1 с показательным:

Рисунок 11- Функция плотности распределения вероятности для гамма распределения в сравнении с показательным

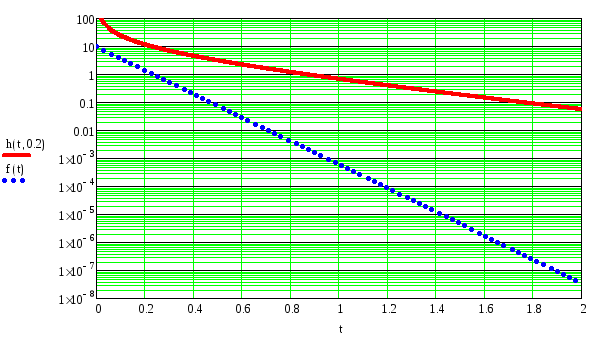
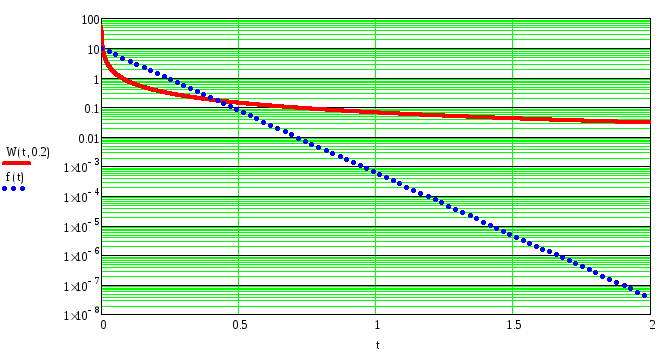
Рисунок 12- Функция плотности распределения вероятности для распределения Вейбула в сравнении с показательным

Рисунок 13 - Функция плотности распределения вероятности для распределения Вейбула в сравнении с показательным

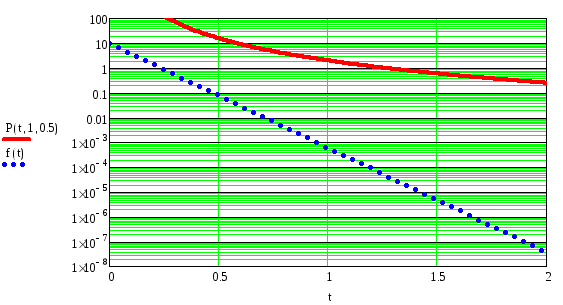
Сравнивая полученные графики, можно сделать следующие выводы: потоки вызовов с данными распределениями обладают свойствами стационарности, однородности, ординарности и за исключением потока вызовов с распределением Парето, потоки без последействия. Функция распределения плотности вероятности интервалов между вызовами для распределения Парето обладает так называемым «тяжелым хвостом», то есть можно сказать, что данный поток вызовов с последействием.

Распределение Эрланга является частным случаем гамма распределения при целых k. Эти распределения, а также распределение Вейбулла при k=1 переходят в показательное, а при устремлении k в бесконечность, стремятся к детерминированному распределению.