4. Элементы регрессионного анализа

   1. Метод наименьших квадратов

Понятия переменной величины и функции являются одними из самых важных в математике, физике, естественных, а последнее время и общественных науках. С помощью этих понятий на основе установленных законов развития и функционирования природы и общества устанавливаются функциональные зависимости между различными рядами данных. Однако далеко не всегда функциональная зависимость между рассматриваемыми данными является уже установленной. В этих случаях возникает задача подбора функциональной зависимости для двух наборов данных.

Независимые переменные x_i в таких задачах называют факторами, а зависимые y_i- откликами. И ставится задача отыскания функции y=f(x), позволяющей предсказывать значение отклика для факторов, не входящих в исходную совокупность. При этом значения функции f(x_i) должны наилучшим образом приближать значения откликов y_i.

Что означают слова «наилучшим образом»? Нужно выбрать критерий, насколько одна функция лучше другой. Для этого рассмотрим набор остатков e_i = y_i- f(x_i). Выбором функции f(x) нужно сделать их как можно меньшими. Но для сравнения качества приближения необходимо свернуть e_i в одну функцию I(e₁, e₂,…, e_n). Просто сложить остатки нельзя, ведь они могут иметь разные знаки, и тогда ошибки могут взаимно компенсироваться. Поэтому надо выбрать либо сумму абсолютных значений остатков, либо сумму квадратов остатков. По ряду причин второй вариант является более предпочтительным. В результате мы приходим к задаче:

I(e₁, e₂,…, e_n)=

Рассмотренный метод называется методом наименьших квадратов.

2. Корреляционная зависимость

Для того, чтобы применение метода наименьших квадратов давало адекватные результаты, необходимо чтобы между числовыми рядами факторов и откликов существовала некоторая зависимость. Проиллюстрируем это на примере.

Совершенно ясно, что между ростом и весом человека существует определенная зависимость. Но столь же ясно, что существует сколько угодно людей с одинаковым ростом, но разным весом. Следовательно, зависимость веса от роста не является функциональной, т.к. функции обладают тем свойством, что до заданному значению независимого переменного х можно найти единственное значение зависимой переменной y. Таким образом, не может быть такой формулы, по которой, зная точный рост, мы находили бы точный вес.

Возможно, скажете Вы, Вес зависит не только от роста, но и от размера талии! Несомненно так, ответим мы, но в то же время можно найти сколь ко угодно людей с одинаковым ростом и одинаковой талией, у которых, тем не менее, вес различный. Следовательно, вес не является функцией только двух переменных — роста и размера талии. Все ясно, скажет читатель: вес зависит от роста, размера талии, объема груди, размера обуви и т.д. и т.п. Вот тут-то мы и подошли к важному выводу: если искомая функциональная зависимость и существует (а пока еще она никем не обнаружена), то она должна быть исключительно сложной.

А поскольку нельзя пользоваться тем, чего нет, то проще описывать эту сложную причинную связь между весом, ростом и другими параметрами человека как-то по иному, минуя классическое определение функции.

Вес и рост человека определяются практически одними и теми же факторами, число которых довольно велико (возраст, наследственность, физиологические особенности, социальные условия, экологическая среда и пр.). Поэтому можно считать, что вес человека зависит от ряда случайных величин, среди которых рост является одной из основных. Эту зависимость описывают с помощью понятия вероятности. Например, имеет смысл говорить о вероятности того, что вес молодого человека с ростом 175 см равен 75 кг или заключен в пределах от 70 до 80 кг. Зависимости такого рода называется стохастическими, вероятностными или статистическими. Они существуют между экологическими параметрами человека, животного, растения; между способностями студента и его успехами в учебе; между отношением сообщества к образованию и уровнем преступности; между внешним видом солдат и боеспособностью полка. Подобных примеров можно привести сколько угодно. Важнейшим видом стохастической зависимости является корреляционная зависимость. Покажем на примере, как описать корреляционную зависимость по результатам наблюдений,

В таблице приведены данные измерения веса и роста двадцати курсантов школы МВД:

Номер	1	2	3	4	5	6	7	8	9	10
Рост	178	170	181	173	169	178	177	165	187	182
Вес	72	65	92	75	68	79	78	67	80	81
Номер	11	12	13	14	15	16	17	18	19	20
Рост	159	182	178	173	176	173	198	187	191	170
Вес	56	82	77	63	80	65	85	89	87	72

Э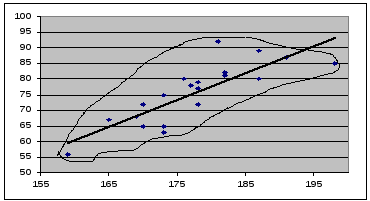ти результаты можно представить графически, построив точки с соответствующими координатами:

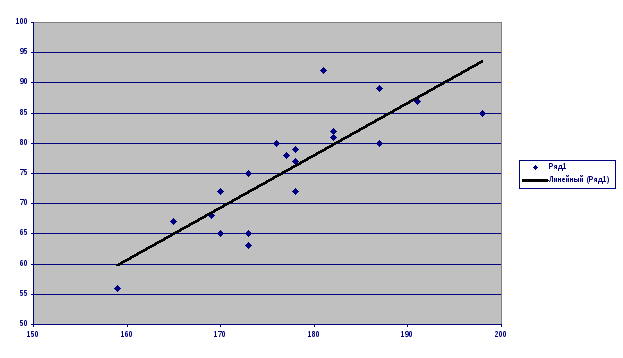
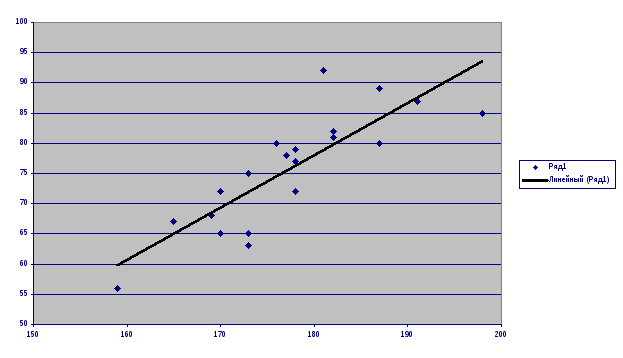
Полученные точки лежат внутри некоторой области или «облака», которое обозначено пунктирной линией. Хорошо заметно, что облако вытянуто вдоль какой-то наклонной прямой. Этот факт означает, что величины Х и У хорошо скоррелированы, т.е. пря увеличении роста вес, как правило, тоже увеличивается. Прямая, вдоль которой вытянулись точки, называется линией регрессии.

Теоретически, каждую точку внутри облака можно считать результатом измерения. При этом допущении линия регрессии, как показывает теория, является прямой. Эта прямая будет графиком некоторой линейной функции, которая называется регрессией. Доказано, что регрессия является наилучшим решением задачи, о которой шла речь в начале этого параграфа — приближенно выразить вес как функцию роста. С помощью уравнения, описывающего эту прямую можно приближенно найти средний вес по заданному росту. Например, определить каким будет вес курсанта с ростом 195 см. Для решения подобных задач определим уравнение этой прямой.

Уравнение искомой прямой имеет вид

y = kx + b,

где

,

Здесь и- средние значения роста, веса и их попарных произведений,D_x- дисперсия роста. Применяя формулы предыдущей главы, получаем

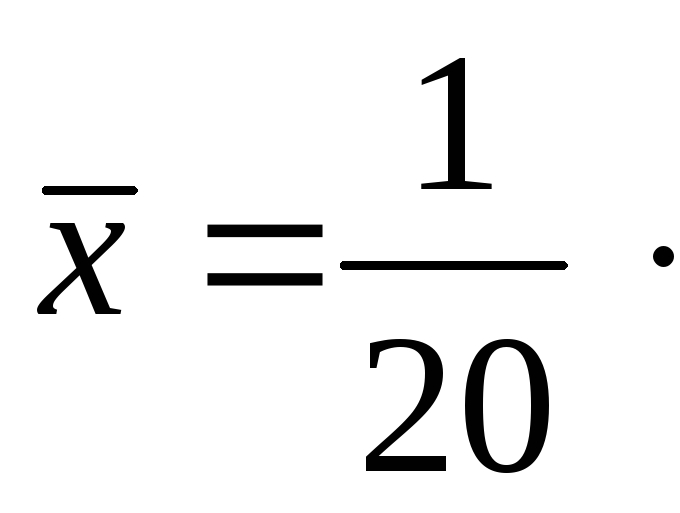(178+170+…+170) = 177,35;

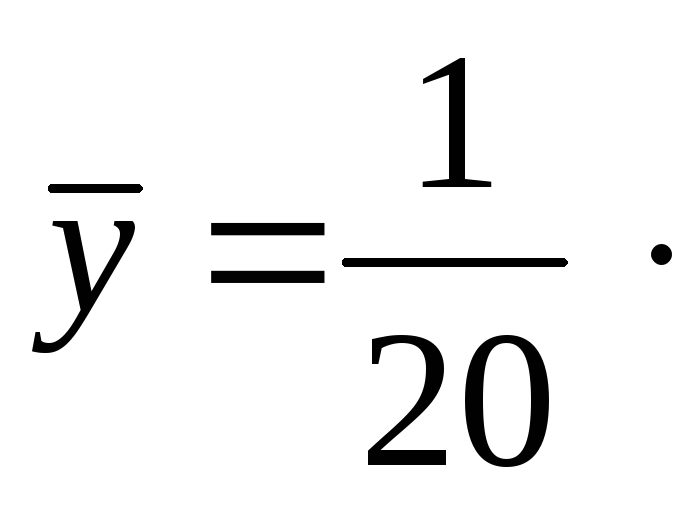(72+65+…+72) = 76,65;

13485,15;

Подставляя полученные значения в предыдущие формулы, находим k и b :

.

Итак, получим следующее уравнение искомой прямой:

y= 0,87x – 78,20.

Она называется эмпирической прямой регрессии. Подставляя в последнее уравнение x = 195, найдем средний вес курсанта с таким ростом – 91 кг.

Весьма важной характеристикой при сравнении двух числовых рядов является коэффициент корреляции, вычисляемый по формуле:

.

Коэффициент корреляции играет важную роль в вопросах математической статистики. Он обладает следующими свойствами:

1. -1  r  1.

2. Если величины Х и У независимы, то коэффициент корреляции между ними равен нулю.

3. Если величины Х я У связаны линейной зависимостью, то коэффициент корреляции равен 1 или -1.

4. Обратно, если коэффициент корреляции равен 1 или -1, то величины Х и Y связаны линейной зависимостью.

При совместном изучении двух случайных величин X и Y прежде всего находят коэффициент корреляции, и если он оказывается близким к единице (по крайней большим 0,5), то имеет смысл описывать корреляционную связь тем способом, который мы только что рассмотрели. Проведенные нами расчеты являются приближенными, и их точность зависит от того, насколько близка эмпирическая линия регрессии к теоретической линии регрессии. Точность повышается при увеличении числа наблюдений, т. е. объема выборки.