Дворецкий - Основы проектирования химических производств - 2005

ϑ

∂cσ

−W

(c

AK

,T) =

∂cσ

;

c

(l, 0) = c0

(l);

c

(0, t) = c0

(t);

(4.70)

∂l

3

∂t

σ

σ

σ

σ

ϑ

∂cχ

−W

(c

AK

,c

D

,T)−W

(c

D

,T) =

∂cχ

;

(4.71)

∂l

4

5

∂t

cχ (l, 0) = cχ0(l); cχ (0, t) = cχ(0)(t);

Составим теперь уравнение динамики для фракции частиц амина, характеризующихся размером от r до r + dr на участке трубы (l1, l2) за время (t1, t2):

t∫2[N(l2, t) ψ(l2, t, r)dr − N(l1, t) ψ(l1, t, r)dr ]dt +

t1

1 t2 l2

+ ϑ ∫∫N(ξ, t) [ψ(ξ, t, r) W1(r)(ξ, t, r)−ψ(ξ, t, r + dr) W1(r)(ξ, t, r + dr)]=

t1 l1

= ϑ1 l∫2[N(ξ, t2) ψ(ξ, t2, r)dr − N (ξ, t1) ψ(ξ, t1, r)dr ]dξ,

l1

которое с использованием приведенной выше техники можно преобразовать к уравнению вида:

(0)

ψ(0,t, r) = ψ

		∂
	ϑ∂ψ(l,t, r) −		ψ(l,t,	r)W(r)(l,t, r)		= ∂ψ(l,t, r) ,	(4.72)
	∂l	∂r		1		∂t
	(t, r); ψ(l, 0, r) = ψ0(l, r).

Получим теперь уравнения динамики теплообмена в трубчатом реакторе:

• по реакционной смеси:

t2		t2 l2
cpρ∫	[T (l2,t)−T(l1,t)]dτ+ ∫∫		[−hSW2(ξ,t)+ K1πD[T(ξ,t)−Tx(ξ,t)]]dξdt =
t1		t1 l1	по хладагенту (х):
	l2
		[T(ξ,t2)−T(ξ,t1)]dξ;
	= cpρS∫
	l1

t2		t2 l2
cxpρxGx ∫	[Tx (l2, t)−Tx (l1, t)]dt − ∫∫		[K1πD[T(ξ, t)−Tx (ξ, t)]]dξdt =
t1		t1 l1
	l2	[T(ξ, t2)−Tx (ξ, t1)]dξ.
= cxpρxSp ∫
	l1

Проводя рассуждения аналогичные предыдущим, получим уравнения динамики теплообмена в процессе диазотирования в трубчатом реакторе:

c

ρG

∂T(l,t)

−hSW (l,t)

+ K πD[T(l,t)−T

(l,t)]= c

ρS

∂T (l,t)

;

(4.73)

∂t

p

l

∂l

2

1

x

p

T(l, 0)

= T

(l); T(0, t) = T(0)(t);

0

cxpρxGx

∂Tx(l,t) − K1πD[T(l,t)−Tx (l,t)]= cxpρxSp

∂Tx (l,t)

;

(4.74)

∂l

∂t

T (l,0)

=T

(l); T (L,t) =T(0)(t).

x

χ0

x

x

Таким образом, уравнения динамики непрерывного процесса диазотирования в трубчатом реакторе представляют собой нелинейные дифференциальные уравнения в частных производных первого порядка, для решения которых можно использовать метод характеристик или конечно-разностные методы

[54].

Уравнения статики легко получить из выведенной системы уравнений динамики приравниванием нулю производной по времени, т.е.

∂∂ct = 0; ∂∂Tt = 0; ∂∂ψt = 0.

Математическая модель статики процесса диазотирования, осуществляемого в трубчатом реакторе, представляет собой систему нелинейных обыкновенных дифференциальных уравнений (4.67′) – (4.74′).

Наибольшую сложность при решении системы дифференциальных уравнений, описывающих статические режимы диазотирования, представляет уравнение, описывающее гранулометрический состав твердой фазы амина в l-м сечении трубчатого реактора

ψ(0, r)

			∂
	∂ψ(l, r)						,	(4.75)
ϑ		=			ψ(l, r) W(r)(l, r)
	∂l		∂r

(0)

=ψ (r).

В случае линейного уравнения кинетики растворения частицы амина

	dr	= −Ar−α exp (− E1 / RT)(c*A −cA)/ρA,	(4.76)
	dt
где A, α – кинетические константы; c*A, cA – равновесная и текущая концентрации амина;			ρA – плотность
амина.

Решение уравнения (4.75) может быть получено методом характеристик в аналитическом виде [54]. Решение уравнения (4.76) запишем в виде

							1
					l
								1+α
					∫A exp(−E1 / RT) (c*A −cA )
					0	~			,
	r (l) = f (r0	, l) = r0α+1 −(1	+α)			dl
					ρA ϑ
	откуда можно рассчитать начальный радиус r0			частицы по формуле

r0 = f1(r, l) = r

l

∫A exp(−E1 /RT) (c*A − cA)

α+1 + (1+ α) 0

ρA ϑ

1

1+α

d~l .

В этом случае решение уравнения (4.75) с начальным условием может быть записано в виде

	(0)			l ∂W(r)		~	~	~		,	(4.77)
ψ(r, l) = ψ		( f1	(r, l)) exp	∫	1	[r(l ,	f1(r, l	)) ]dl
					∂r
				0

В случае нелинейного уравнения кинетики растворения частицы, например, в виде

dmdt = −β* (c*A − cA) S ,

где β – эффективный коэффициент массоотдачи; S – поверхность частицы, необходимо использовать численный алгоритм решения уравнения (4.75).

Аппроксимируя дифференциальные уравнения в частных производных (4.75) конечной системой дифференциальных уравнений в обыкновенных производных с использованием конечно-разностной схемы первого порядка, получим

r

+ r

∂W (r)

d ψ

i

ψ

−ψ

i−1

=W (r)

i

i−1

, c

, c

i

−

1

(r , c

, c

)ψ

,

dl

2

∆r

∂r

1

A

AK

i

A

AK

i

i

(0)

(4.78)

– шаг сетки.

ψ1(0)

= ψ (ri , l), ∆ri

Полученная система обыкновенных дифференциальных уравнений (4.78) одновременно с другими уравнениями модели может быть решена каким-либо численным методом. При этом могут возникнуть сложности, поскольку в начальной фазе процесса диазотирования скорость растворения твердой фазы и скорость реакции диазотирования различаются на несколько порядков, т.е. система дифференциальных уравнений математической модели процесса диазотирования является жесткой. В этом случае явные методы Рунге-Кутта исключаются из рассмотрения.

Для решения системы дифференциальных уравнений модели статики процесса диазотирования можно рекомендовать два метода: неявный метод трапеций и метод Дормана-Принса пятого порядка точности с автоматическим выбором шага, которые дают вполне сопоставимые результаты и обеспечивают получение решения с заданной точностью.

Математическая модель динамики процесса диазотирования, осуществляемого в турбулентном трубчатом аппарате, включает нелинейные дифференциальные уравнения с частными производными (4.67) – (4.74), для решения которых целесообразно использовать конечно-разностный метод [55].

Для математического описания процесса диазотирования, осуществляемого в турбулентном трубчатом реакторе комбинированного типа, необходимо к уравнениям (4.67) – (4.74) добавить уравнения, описывающие протекание процесса диазотирования в камере смешения.

В неустановившемся режиме текущий радиус частицы r кроме начального значения r0 зависит также от возраста частицы τ и текущего времени t. Кинетика растворения частицы описывается квазилинейными дифференциальным уравнением с частными производными первого порядка

∂r +	∂r =W (r, c			, c	A	,T),	(4.79)
∂t	∂τ	1	CK

где W1 – скорость растворения частицы; cCK , cA – концентрации соляной кислоты и амина, соответст-

венно; T – температура.

Начальные условия определим следующим образом:

t0 = 0, τ = τ0, r(τ0) = r0(τ0).

(4.80)

Решение уравнения (4.79) при заданных начальных условиях (4.80) имеет вид

r(α+1) (τ, t)

r

α+1

(τ

0

)

t

~

*

~

~

0

− A ∫exp(−E1 /

=

RT(t ) (cA(cCK

,T)−cA(t ))dt ;

α +1

α +1

0

где

t

~

~

~

~

~

W1(r, cCK , cA,T) = −A∫exp(−E1 /

*

RT(t ) (cA(cCK (t ),T

(t ))−cA(t )) dt .

0

Учитывая, что τ−τ0 = t −t0,

получим τ0 = τ−t +t0

и

r(α+1)(τ,t)

r0α+1

(τ−t)

t

~

*

~

~

~ ~

=

− A∫exp(−E1 /RT(t ) (cA(cCK (t ),

T(t ))−cA

(t ))dt .

α+1

α+1

0

Плотность распределения массы частиц в каждый момент времени описывается дифференциальными уравнениями, получаемыми из материального баланса для фракции частиц

		∂ ψW1			(0)
∂ψ(r,t)
	=			+ n(0)	ψ	(r,t)−ψ(r,t)/θ(t),	(4.81)
∂t		∂r

где θ(t) – среднее время пребывания частиц в модуле-реакторе. Решением уравнения (4.81) при начальных условиях (4.80) будет

	= exp [F(0,t, r, cCK , cA,T)			{ψ0 [ϕ(0,t, r, cCK , cA,T)]}]+
ψ(r,t)
t (0)	~	~		~	~
∫Gs	[ϕ(t ,t, r, cCK , cA,T), t		]exp[F (0, t , r, cCK , cA,T), cCK ,T]dt ,
0

(4.82)

где

F(0,t, r,cCK ,cA,T) = ∫t {W1r [ϕ(~t ,t, r,cCK ,cA,T),cCK ,cA,T]+1/θ(~t )}d~t ,

0

W1r = dW1 /dr = α Ar−(α+1) exp(−E1 /RT) (c*A(cCK ,T)−CA).

Подставляя зависимости (4.82) в уравнения покомпонентного материального и теплового балансов, получим:

&

rmax

(0)

(0)

/V −

cA =

∫ ψ(r,t)W1(r,cCK,cA,T)dr/V +cA

Gi

0

−W2(cA, cAK ,T)−cAGl ;

(4.83)

сA(0) = cA 0;

&

(0)

(0)

(0)

(0)

cAK = cAKGl

/V + cN

GN /V −(W2(cA, cAK ,T)+

(4.84)

+W3(cAK ,T)+W4(cA, cD,T)−cAKGl /V ;

сAK (0) = cAK 0;

&

(0)

(0)

(0)

(0)

(4.85)

cCK = cCKGl

/V −cN GN

/V −W2(cA, cAK ,T)−cCKGl /V;

сCK (0) = cCK 0;

&

(0)

(0)

/V

+(W2(cA, cAK ,T)−W4

(cAK , cD,T)−W5(cD,T))−cDGl /V;

cD = cD

Gl

(4.86)

сD (0) = cD 0;

&

(0)

(0)

/V +W4

(cAK , cD,T)+W5(cD,T)− cχGl /V;

(4.87)

cχ = cχ

Gl

сχ (0) = cχ 0;

&	(0) (0)		/V + c	N	G	(0)	T	(0)	/c V −GT /V +
T	= G T			v		N		N
		l							v	l
	+	W2(cA, cAK ,T)h2				+	W3(cAK ,T)h3				− KF (T −T )/c V; (4.88)
		cvV							cvV		x v

T(0) =T0;

T&	= G(0)T(0)	/V	p	−G T /V	p	+ KF(T −T )/cxV		p	;	(4.89)
x	x x			x x		x	v

Tx (0) = Tx 0;

Система нелинейных дифференциальных уравнений (4.82) – (4.89) представляет собой математическую модель динамики процесса диазотирования, осуществляемого в камере смешения.

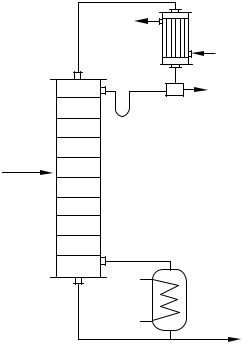
7. Модель процесса бинарной ректификации [56, 57]. Ректификацией называется процесс переноса компонента (компонентов) между кипящей жидкой и насыщенной конденсирующейся паровой фазами при противотоке этих фаз. Ректификацию можно трактовать как совмещение процессов многократной дистилляции и многократной парциальной конденсации при противоточном контактировании потоков пара и жидкости. Дистилляция представляет собой частичное испарение (при температуре кипения) жидкой смеси. пар при этом в соответствии с первым законом Коновалова обогащается низкокипящим компонентом (или азеотропом с минимумом температуры кипения), а жидкий остаток – высококипящим компонентом (или азеотропом с максимумом температуры кипения). В этом и состоит эффект разделения.

Для определенности будем рассматривать тарельчатую ректификационную колонну, содержащую n тарелок, в которой происходит разделение бинарной смеси (рис. 52). Исходное питание в количестве Gp

состава xp подается на f-ю тарелку. Сверху колонны отбирается дистиллят в количестве GD состава xD , а снизу колонны – кубовый продукт в количестве Gw состава xw .

Ln+1, xn+1 GD, xD

Gр, xр

Gw, xw

Рис. 52. Схематическое изображение ректификационной установки

Математическая модель может быть построена для ряда конструкций контактных устройств (тарелок) в зависимости от принятых допущений. Для характеристики интенсивности массообмена на контактном устройстве вводится понятие эффективности тарелки, которое определяется следующим образом:

ηj = ((yyj − yyj−1)) ,

j − j−1

где yj−1, yj − составы паровой фазы, поступающей на тарелку и покидающей ее, соответственно; yj − концентрация в паре, равновесная с жидкостью, находящейся на j-й тарелке.

Исходные данные: известна зависимость равновесного состава пара от состава жидкости для заданного давления в колонне: yj = yj (xj ); количество питания Gp , его состав xp , величина отбора дистиллята

GD и скорость пара v в колонне, определяемая количеством тепла, подводимым к кубу.

Требуется построить математическую модель, позволяющую по исходным данным рассчитывать

составы жидкости xj			и пара yj на всех n тарелках колонны, составы получаемых продуктов, т.е. дис-
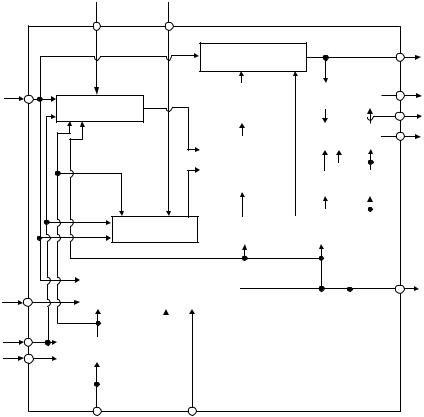
тиллята xD и кубового остатка xw (рис. 53), для заданных условий разделения.
Qк							GD; xD, i; TD
			ДЕФЛЕГМАТОР
VN; yN, i; TY, N					LN+1, xN+1, i
				j = N
VN-1				UN-1	LN
Vj				Uj	Lj+1
				j > f
Gр, xр, i		Vf	yf, i	Uf, xf, i	Lf+1; xf+1, i
			VF	j = f
			LF
Vf; yj, i;			Ty, j	Uj, xj, i	Lj+1; xj+1, i;Tx, j+1
				j < f
		V1	y1, i	U1, x1, i	L2; x2, i; Tx, 2
				j = 1
		Vw	V0 = VW		L1
Qw							Gw; xw, i; Tw
			КИПЯТИЛЬНИК

Рис. 53. Структурная схема ректификационной установки

При построении математического описания примем следующие основные допущения:

1)давление на контактном устройстве постоянно;

2)жидкость находится при температуре кипения, пар – при температуре точки росы;

3)разделяемые смеси близки к идеальным;

4)физико-химические свойства компонентов постоянны на данном контактном устройстве и усреднены в возможном диапазоне изменения концентраций;

5)жидкость на тарелках колонны, а также в кубе и флегмовой емкости идеально перемешана;

6)движение потока пара при его контакте с жидкостью на тарелках может быть описана гидродинамической моделью идеального вытеснения;

7)массопередача по фазам независимая, диффузионные сопротивления аддитивны;

8)интенсивность массообмена между жидкостью и паром на тарелке характеризуется объемным коэффициентом массопередачи Ky, значение которого постоянно для всех точек массообменного про-

странства тарелки;

9)куб колонны работает как парциальный испаритель;

10)в конденсаторе колонны происходит полная конденсация и дистиллят отбирается в жид-

кой фазе;

11)пар равномерно распределяется по всему массообменному пространству тарелки;

12)теплоты смешения потоков жидкости пренебрежимо малы;

13)режим работы контактного устройства – адиабатический.

Для стационарного режима система уравнений математического описания тарелки имеет вид:

V

j−1

+U

j

−1

+G ,

j < f ;

W

Lj =

+U

− L

,

j > f ;

V

j−1

j

−1

n+1

(4.90)

(V

y

+U

x

+G x )/ L

j−1

j−1

j−1

j−1

j

, j < f ;

W 0

xj =

+U j−1 xj−1 − Ln+1 xn+1)/ Lj, j > f ,

(Vj−1 yj−1

где V − расход пара; U − унос жидкости; L− расход жидкости;

f − номер тарелки питания;

флегмы.

Уравнение для расчета состава пара, уходящего с тарелок имеет вид:

yj = yj−1 + (yj − yj−1) ηj;

j ≠ f ;

ηj

=1−exp(Kyj /Vj−1);

Kyj = Sj

1

βyj + mj /βxj

1/

∂y

m

j

=

;

y

j

= y

j

(x

j

);

∂x

x=xj

βyj = βyj(Vj−1,Lj,xj, yj−1);

βxj = βxj(Vj−1,Lj,xj, yj−1),

j =1, ..., n,

j ≠ f ;

U j

=U j (Vj ),

Ln+1 − расход

;

(4.91)

где Ky − коэффициент массопередачи; βx − коэффициент массоотдачи по жидкой фазе; βy − коэффициент массоотдачи по газовой фазе; η− эффективность контактного устройства; S − эффективная площадь та-

релки.

Уравнения теплового баланса на тарелках колонны

Vj = (Vj−1(Hj−1 −hj)+Uj−1(hj−1 −2hj +hj+1)+GW (hj+1 −hj))/(Hj −hj+1), j < f;

Vj (H j − hj+1)=Vj−1 (H j−1 − hj )+U j−1 (hj−1 − 2hj + hj+1)−
− Ln+1 (hj+1 − hj )+VF (HF − hj )	при j > f ;

H j = H j(Tx j ,Ty j ,rj ); hj = hj (Txj ,Ty j ); Tx j =Tx(xj );

Ty j =Ty(yj ); rj = r(xj); j =1, 2, ..., n, j ≠ f ,

где h, H − энтальпии жидкости и пара.

Величина уноса U в (4.91) зависит от конструктивных особенностей контактного устройства, физи- ко-химических свойств компонентов и может быть определена по уравнениям, приведенным, например, в [58.]

Приведенная выше модель контактного устройства может быть использована для тарелки питания только при учете специфики энергетического состояния питания, подаваемого в колонну. Для данного случая уравнения модели тарелки питания имеют следующий вид:

Vf =	Vf −1 (H f −1 − hf		)−U f −1 (hf −1 − 2hf + hf		+1)+	+
			H f − hf +1
+		GW (hf +1 − hf )	+ LF (hf − H f −1)	+Vf ;
		H f − hf −1
yf = [(yf −1 + (y − yf −1)ηf )(Vf −VF )+Gp (1− q)yF ]
		yF = [α1 −(α1 − 4α2α3)0,5]/(2α2);
α1 = (α −1)(xp − q)+ α; α2 = (α −1)(1− q); α3 = α
	VF = (1− q)Gp;		xF = [xp −(1− q)yF ]/q;

xf = (Vf −1 yf −1 +U f −1 xf −1 +GW x0 ); Lf =Vf −1 +U f −1

/Vf ; xp;

+GW .

(4.92)

В простейшем случае уравнение, описывающее систему дефлегматор-конденсатор емкость, может быть представлено в виде

xD = yn + (yD − yn)ηD ,

(4.93)

где ηD − эффективность дефлегматора, 0 ≤ ηD ≤1.

Возможны частные случаи:

1) ηD = 0 , что обычно справедливо для полного конденсатора, в этом случае xD = yn ; 2) ηD =1, что справедливо для парциального конденсатора, тогда xD = yD .

В простейшем случае уравнение, описывающее куб колонны, может быть представлено в виде

y0 = x0 + (y (x0)− x0 )η0 ,

(4.94)

где η0 − эффективность кипятильника, 0 ≤ η0 ≤1. Частные случаи:

1)η0 = 0 , что обычно справедливо для полного испарителя, т.е. y0 = x0 ;

2)η0 =1, что справедливо для парциального испарителя, тогда y0 = y (x0).

Для построения математической модели всей установки необходимо описание отдельных частей установки дополнить уравнениями связи. В качестве таких уравнений обычно используют общие уравнения материального и теплового балансов для всей установки. Специальный выбор вида уравнений, описывающих контактные устройства в рекуррентной форме, позволяет отказаться от записи уравнений связи между контактными устройствами, поэтому приводим только общие уравнения:

Gf = GW +GD; Gp xp = GW x0 +GD xD; xD = xn+1; Ln+1 =Vn −GD;

LF h(xf )+VFH (yf )+QW =GD h(xD)+GW h(x0)+Qk +Qпот,

(4.95)

где QW ,Qk − расходы тепла в кипятильнике и конденсаторе, соответственно; Qпот− потери тепла.

Приведенная система уравнений при сделанных выше предположениях полностью описывает стационарный режим работы колонны и может быть использована для решения различных задач компьютерного моделирования. Блок-схема расчета уравнений модели процесса ректификации (4.90) – (4.95) для i < f представлена на рис. 54.

yj-1

xj-1

Vj-1

Uj-1

βy βx

βy (Vj−1,Lj ,xj ,yj−1)

βx (Vj−1,Lj ,xj ,yj−1)

yj

yj = yj−1 −(y*j −yj−1)ηj

Uj

Kyj

Tyj (yj )

Uj(Vj )

ηj =1−eVj

hj

Vj

H j ,hj

V j

Kyj = Sj

1

1

+

mj

βy

βx

Txj (xj )

rj (xj )

mj (xj )

y*j = y(x j )

									xj
	xj =		1	(Vj−1 yj−1 +U j−1 xj−1 +Gw x0 )
			Lj
L j = V j−1 + U j−1 + G w

Gw x0

Рис. 54. Блок схема решения уравнений модели процесса ректификации (4.90) – (4.95) для i < f

Моделирующий алгоритм в данном случае должен в принципе обеспечивать возможность решения представленной системы алгебраических уравнений математического описания при любых значениях задаваемых параметров. Наиболее просто эта система может быть решена с использованием итерационного метода расчета "от тарелки к тарелке". Задается состав кубового остатка x0 и далее по блок-схеме

(см. рис. 54) рассчитывается состав жидкости x1 на первой тарелке колонны, состав пара, уходящего с

тарелки, и состав жидкости на вышележащей тарелке. Эта расчетная процедура повторяется для всех тарелок колонны, включая и тарелку питания (4.92), в результате чего находится состав дистиллята по формуле (4.93) или xD = xn+1, Ln+1 =Vn −GD по формулам (4.95). Затем проверяется выполнение уравнения

общего материального баланса колонны (4.95) для заданного состава кубового остатка и полученного расчетным путем состава дистиллята. Если баланс не выполняется с заданной точностью, расчет повторятся с измененным соответствующим образом составом кубового остатка, начиная с первого этапа, до тех пор пока общий материальный баланс колонны не будет сведен с заданной точностью.

Заметим, что каждая итерация сопровождается расчетом по всем тарелкам колонны. Разумеется, что эффективность предложенного алгоритма существенно зависит от того, насколько эффективен способ уточнения кубового остатка.

8. Модель процесса сушки дисперсных материалов в неподвижном слое [59]. Анализ процесса сушки дисперсных материалов в неподвижном слое является основным элементом моделирования тепло- и массообмена в сушилках с перекрестным движением материала и сушильного агента.

Для описания кинетики сушки отдельной частицы принимается уравнение, соответствующее периоду постоянной скорости сушки при условии, что вся теплота, конвективно подводимая к поверхности влажной частицы, затрачивается на испарение влаги:

	−	du	= αF (t −tм)/(V ρT rc) ,	(4.96)
		dτ

где F, V, ρT и u – площадь поверхности, объем, плотность и влагосодержание частицы; t − температура

сушильного агента; α – коэффициент теплоотдачи от сушильного агента к поверхности влажной частицы;

rc – теплота испарения; tм – температура мокрого термометра.

Интегрирование уравнения (4.96) для сферической частицы диаметром d при начальном условии u |τ=0= u0 дает текущее значение влагосодержания частицы с учетом возможного изменения температуры

сушильного агента t у ее поверхности:

		6α	τ
u = u0 −			∫(t −tм)dτ .	(4.97)
	r	ρ d
	c	T	0

Распределение температуры сушильного агента по высоте слоя материала (для определенности здесь полагается, что сушильный агент фильтруется через слой снизу вверх) определяется из уравнения теплового баланса для элементарного слоя dh в предположении режима полного вытеснения при фильтрационном движении сушильного агента через слой:

−cGdt = α(t −tм)[6(1−ε)/d]dh,

(4.98)

где 6(1−ε)/d − поверхность монодисперсных сферических частиц, приходящихся на единицу высоты

слоя.

Интегрирование уравнения (4.98) дает экспоненциальный профиль температуры сушильного агента по высоте h слоя порозностью ε:

t = tм + (t0 −tм) exp(−Bh) .

(4.99)

В этих уравнениях B = 6α(1−ε)(cGd) , с, G и t0 – теплоемкость, расход и температура поступающего в

слой сушильного агента.

С учетом стационарного распределения температуры (4.99) по формуле (4.97) получим значение влагосодержания материала на высоте слоя h:

u = u0 −[6α (rc ρT d)] (t0 −tм) exp(−Bh)τ .

(4.100)

Величина среднего влагосодержания всего слоя материала высотой Н находится интегрированием распределения (4.100) по высоте в пределах 0 ≤ h ≤ H :

			1	H	cG(t0 −tм )				−BH
	u =			∫udh = u0 −				(1−e		)τ .	(4.101)
			H		r ρ	T	(1−ε)H
				0	c

Уравнения (4.100) и (4.101) описывают процесс сушки до момента времени τ*, когда нижний слой частиц достигает равновесного влагосодержания u*. Значение τ* находится из распределения (4.100) при h = 0 и u = u*: