Лекция10_ТеорияПоля

Теория поля

Скалярное поле

Совокупность точек пространства, в каждой из которых задана скалярная функция независимо от физического смысла этой функции она называется потенциалом скалярного поля. Геометрическое место точек, в которых функция принимает постоянное значение называется поверхностями уровня, а для плоских полей – линиями уровня. Если функция не зависит от времени, то поле называется стационарным, в противном случае – нестационарным.

Пример. Найти поверхности уровня функции .

Решение

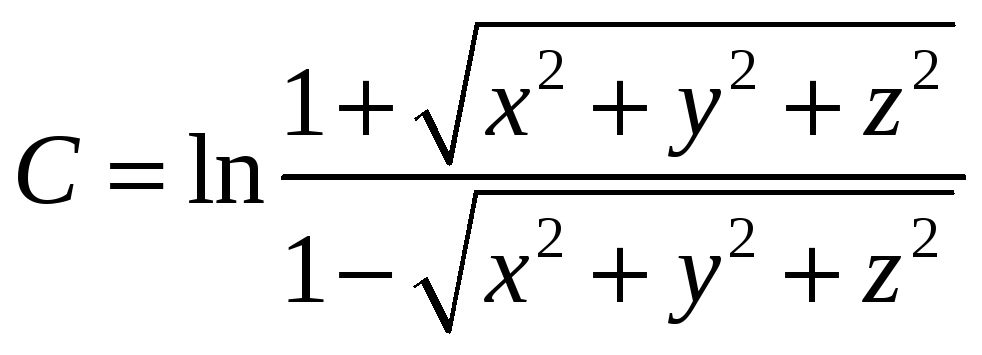
, можно принять, что ,

.

Для данного поля поверхности уровня – сфера.

Производная по направлению

Пусть в некоторой области задана функция , которая непрерывна и имеет непрерывные частные производные в этой области. Выберем в этой области произвольную точку и проведем вектор .

Производной от функции по направлению вектора называется:

.

Производная по направлению определяет скорость изменения функции в направлении вектора .

Пример. Найти производную от функции в точке по направлению вектора .

Решение

, ,

, , , . .

Градиент функции

Градиентом функции называется вектор проекциями которого на оси координат являются частные производные от функции .

.

Градиент указывает на наибольшую скорость изменения функции.

Установим зависимость между производной по направлению и градиентом. Для чего на векторе выберем единичный вектор . Вычислим скалярное произведение на .

.

Обозначим .

. Из последних двух равенств имеем:

.

Векторное поле

Под векторным полем понимается совокупность точек пространства каждой из которых соответствует определенный вектор. Например, в гравитационном поле в каждой точке можно изобразить вектор силы действующий на единицу массы, помещенный в это поле. В электрическом поле в каждой точке можно построить вектор напряжения. Кроме силовых полей существуют и другие например поле скоростей текущей жидкости. Векторное поле считается заданным, если в каждой точке определен вектор , где - функции зависящие от координат точки. Будем предполагать, что эти функции непрерывные. Если эти функции зависят от двух переменных, то рассматривается плоское поле, с плоскими полями встречаются в гидродинамике. Векторные поля изображаются векторными линиями.

Векторные линии – линии в каждой точке которых касательная совпадает с направлением вектора приложенного к этой точке.

Выведем уравнение векторных линий.

Пусть задано векторное поле . Проведем радиус вектор к точке . Известно, что это вектор направленный по касательной к линии , а также вектор образующий поле, по определению векторной линии, также направлен по касательной к ней. Следовательно, и - коллинеарны:

- уравнение векторных линий.

Пример. Найти векторные линии поля .

Решение

, , .

или , .

Поверхностные интегралы

Поток вектора через поверхность

Пусть в пространстве задано поле скоростей текущей жидкости, которое определяется вектором :

, где , , - непрерывны.

Пусть в этом пространстве определена некоторая поверхность . Определим количество жидкости, которое протекает через поверхность в единицу времени, то есть определим поток жидкости через поверхность - поток .

Разобьем поверхность произвольным образом на частей: , ,…, . Выберем на каждом участке разбиения точку . Будем предполагать, что участки плоские, а векторы скорости на каждом из участков разбиения постоянны и совпадают с вектором вычисленным в точке . Тогда элементарный поток через -ую площадку будет равен объему цилиндра с основанием и высотой равной проекции вектора на единичный вектор нормали к поверхности :

. Пусть единичный вектор имеет координаты . Тогда . Поток через всю поверхность определяется:

(1)

Чтобы определить точное значение следует перейти в равенстве (1) к пределу, когда максимальное значение . Если такой предел существует, то он называется поверхностным интегралом первого рода (или по площади поверхности) и обозначается

Зависимость между поверхностными интегралами первого и второго рода

Известно, что , , .

Интеграл стоящий в правой части называется поверхностным интегралом второго рода по координатам.

Свойства поверхностного интеграла

1), - площадь поверхности

2)

3)

4) Если поверхность разбита на части, то поверхностный интеграл по всей поверхности равен сумме интегралов по ее частям.

5) Если , то

6).

7)Теорема о среднем в поверхностном интеграле: Если функция непрерывна на поверхности , то найдется, по крайней мере одна точка , лежащая на поверхности , то , где - площадь данной поверхности.

Вычисление поверхностных интегралов первого рода.

Пусть требуется вычислить по поверхности , которая задана уравнением . Предположим, что поверхность пересекается прямыми параллельными не более, чем в одной точке.

.

.

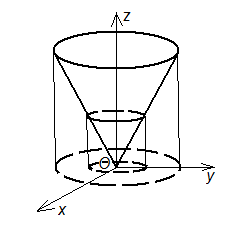
Пример. Вычислить поверхностный интеграл по поверхности конуса и плоскостям , .

Решение

Двухсторонние и односторонние поверхности

Пусть задана гладкая поверхность . Возьмем на этой поверхности некоторую точку . Проведем нормаль в точке к этой поверхности и выберем определенное направление этой нормали. Будем перемещать нормаль вдоль замкнутого контура , который не пересекает границ поверхности , если нормаль возвращается в исходное положение с тем же направлением, то поверхность двусторонняя. Если же нормаль возвращается в исходное положение с противоположным направлением, то такая поверхность – односторонняя.

Двухсторонняя поверхность у которой выбрано определенное направление нормали называется ориентированной поверхностью. За положительное направление принимается такой контур, проходя по которому область остается слева.

Свойства поверхностных интегралов второго рода

Все свойства перечисленные для поверхностных интегралов первого рода совпадают со свойствами поверхностных интегралов второго рода.

Если изменить сторону поверхности , то поверхностный интеграл изменит свой знак на противоположный.

Замечание:

, если - цилиндр с образующей параллельной оси .

, если - цилиндр с образующей параллельной оси .

, если - цилиндр с образующей параллельной оси .

Вычисление поверхностного интеграла второго рода

Пусть требуется вычислить

.

Распишем этот интеграл на сумму интегралов

. Рассмотрим по слагаемым

. Если единичный вектор нормали к поверхности имеет координаты , то знак «+» соответствует острому углу . Знак «-» соответствует тупому углу . Если поверхность задана уравнением , то , ,.

Если поверхность задана уравнением :, .

Знаки будут соответствовать внешней и внутренней стороне поверхности.

Пример

Вычислить по верхней стороне части плоскости:

, лежащей в первом октанте и отсекаемой плоскостью

Решение

Циркуляция векторного поля

Пусть векторное поле задано вектором . Выберем в этом поле линию и вектор направленный по касательной к кривой : .

. Интеграл в правой части представляет собой работу по перемещению материальной точки вдоль кривой , если контур замкнутый, то

- называется циркуляцией вектора (циркуляцией векторного поля). Криволинейный интеграл по замкнутому контуру от скалярного произведения вектора образующего поле на вектор касательный к контуру называется циркуляцией вектора вдоль контура или .

Дивергенция векторного поля

Пусть векторное поле задано вектором . Будем рассматривать его как поле текущей жидкости. Поток вектора через некоторую поверхность в данном вектором поле может быть положительным , это значит, что имеется источник. Если , то в выделенном объеме имеются стоки. Если , то в выделенном объеме нет ни источников ни стоков, или их мощности таковы, что они компенсируют друг друга. Поэтому для характеристики потока вводят понятие мощности, то есть такое количество жидкости, которое протекает через поверхность в единицу времени.

Плотность источника определяется по формуле:

.

Чтобы определить плотность источника в точке следует перейти к пределу когда объем стягивается в точку и этот предел называется дивергенцией (расходимостью векторного поля).

.

Дивергенция величина скалярная и вычисляется по формуле:

.

Если дивергенция равна 0, то поле называется соленоидальным.

Пример. Вычислить дивергенцию поля линейных скоростей.

Решение

Ротор (вихрь) векторного поля

Ротором или вихрем векторного поля называется вектор, проекциями которого на оси координат являются разности частных производных:

.

или ,

где .

Если ротор равен нулю, то векторное поле называется потенциальным или без вихревым.