44. Свободные затухающие колебания

Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, постепенно расходится на нагревание. Свободные колебания будут затухающими.

Уравнение данного колебательного контура мы получим, положив в уравнение (5) .

Тогда

. (11)

Решение этого однородного дифференциального уравнения при имеет вид

, (12)

где  - частота затухающих колебаний:

, (13)

где и - произвольные постоянные, определяемые из начальных условий. График функции (12) показан на рис. 16.3.

Рис. 16.3

Видно, что эта функция не периодическая, она определяет затухающие колебания.

Величину условно называют периодом затухающих колебаний:

, (14)

где - период свободных незатухающих колебаний.

Множитель в уравнении (11) называютамплитудой затухающих колебаний. Зависимость ее от времени показана штриховой линией на рис. 16.3.

Напряжение на конденсаторе и ток в контуре. Зная , можно найти напряжение на конденсаторе и ток в контуре. Напряжение на конденсаторе

. (15)

Ток в контуре

.

Преобразуем выражение в квадратных скобках к косинусу. Для этого умножим и разделим это выражение на , а затем введем уголпо формулам

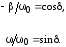(16)

После этого выражение для I примет вид

. (17)

Из выражения (16) следует, что угол  лежит во второй четверти (). Это означает, что при наличии активного сопротивленияR ток в контуре опережает по фазе напряжение (15) на конденсаторе более, чем на . При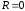опережение. Графики зависимостейиимеют вид, аналогичный рис. 16.3.

Величины, характеризующие затухание:

1. Коэффициент затухания  и время реакции  - время, за которое амплитуда колебаний уменьшается в е раз. Из формулы (12) следует, что

. (18)

2. Логарифмический декремент затухания . Он определяется как натуральный логарифм отношения двух значений амплитуд, взятых через период колебания Т:

, (19)

где а – амплитуда соответствующей величины (q, U, I). Или иначе:

,

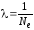где - число колебаний за время, т.е. за время, в течение которого амплитуда колебаний уменьшается в е раз. Это легко получить из формул (18) и (19). Если затухание мало (), тои. согласно формуле (19)

. (20)

3. Добротность Q колебательного контура. По определению

,

где  - логарифмический декремент затухания. Чем меньше затухание, тем больше Q. При слабом затухании (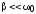), согласно выражению (20) добротность

.

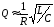И еще полезная формула для Q в случае слабого затухания:

,

где W – энергия, запасенная в контуре; W – уменьшение этой энергии за период колебания Т. В самом деле, энергия W пропорциональна квадрату амплитуды заряда конденсатора, т.е. . Отсюда относительное уменьшение энергии за период.

При вместо колебаний будет происходитьапериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим:

.

Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы автоколебания – незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями). Автоколебательными системами являются часы, двигатели внутреннего сгорания, паровые турбины, ламповые генераторы и т.д.