3.4. Пошук максимальної течії в мережах. Розрахунки у мережах.

Зважені графи є непоганою моделлю, що дозволяє проводити розрахунки в мережах, які є зручною моделлю при дослідженні цілого ряду задач у транспорті, зв’язку, плануванні та інших областях, що пов’язані з дійсним або уявним рухом товарів, інформації, людей. Найчастіше серед поміж інших мереж виділяють транспортну мережу та мережеве планування. В даному підрозділі розглянемо алгоритми розв’язку задач, пов’язаних з цими мережами, а саме задачі знаходження максимальної течії в мережі та задачі мережевого планування.

Спочатку розглянемо задачу пошуку максимальної течії в мережі. Введемо необхідні визначення та позначення.

Мережею будемо називати орієнтований зв’язний простий граф (тобто граф без петель та кратних ребер). В мережі кожному ребрупоставлена у відповідність йогопропускна здатність – невід’ємне дійсне число ; якщо ребране існує, то вважають, що. Виділяють дві вершини:джерело, яке ми позначатимемо через тастік (позначатимемо через ). Всі інші вершини мережі називаютьпроміжними. Як і інші зважені графи мережі будемо задавати або діаграмою, на якій позначатимемо пропускну здатність кожного ребра, або матрицею.

Течією в мережі називається дійсна функція, яка має такі властивості:

а) обмеження пропускною здатністю: для будь-яких вершин тавиконується нерівність;

б) асиметричність для будь-яких вершин тавиконується рівність;

в) збереження течії: для будь-якої проміжної вершини виконується рівність, тобто сума всіх течій що входять до вершинидорівнює сумі всіх течій, що виходять з неї.

Найбільш зручно зображати течії на діаграмі графа із вказівкою напрямку у вигляді «величина течії» / «пропускна здатність».

Сумарною величиною течії називається сума всіх течій, що відходять від джерела:. Доведено, що величина течії також дорівнює сумі всіх течій, що входять до стоку, тобто. Задача промаксимальну течію полягає в знаходженні такої множини течій, щоб при цьому була максимальною.

Для більшої зрозумілості задачі розглянемо ситуацію, для якої мережа є найбільш вдалою моделлю та наведемо інтерпретації. Існують нафтова свердловина (джерело) та нафтопереробний завод (стік). Свердловина виробляє нафту, завод її споживає. Свердловина та завод пов’язані системою трубопроводів, на шляху від свердловини до заводу труби можуть сходитися та розходитися (у проміжних вершинах мережі). Труби можуть мати різні діаметри та інші характеристики, тому їхня пропускна здатність може бути різною. Вважаємо, що джерело може виробити, а стіл спожити необмежену кількість продукції за одиницю часу, обмеження лише у пропускній здатності труб (на практиці це найбільш частий випадок). Треба знайти максимальну кількість нафти, яку можна передати за одиницю часу від джерела до стоку, та як це зробити.

В 1955 році Форд та Фалкерсон знайшли алгоритм розв’язку цієї задачі. Це був перший алгоритм, що майже завжди давав непоганий результат (як за значенням відповіді, так і за складністю виконання), проте цей алгоритм мав свої недоліки, які ми наведемо нижче.

Для розгляду кроків алгоритму Форда – Фалкерсона розглянемо наступні визначення. Аргументальним ланцюгом називається простий шлях від до, вздовж якого можна збільшити течію без перевершення пропускної здатності кожної дуги.Залишковою (за течією ) називається мережа, у якій пропускна здатність кожного ребрадорівнює величині.

Розглянемо кроки алгоритму Форда – Фалкерсона.

Алгоритм 3.8. (Форда – Фалкерсона) Відшукання максимальної течії в мережі.

Спочатку всі течії дорівнюють 0. Залишкова мережа співпадає з початковою мережею.

Крок 1. Знаходимо аргументальний ланцюг у залишковій за течією мережі.

Крок 2. За ланцюгом збільшуємо течіюна максимально можливу величину, перераховуємо залишкову мережу та переходимо до кроку 1.

Алгоритм закінчує свою роботу у випадку, коли крок 1 виконати неможливо, тобто аргументального ланцюга у залишковій мережі більше не існує. Одержана таким чином течія буде максимальною. ■

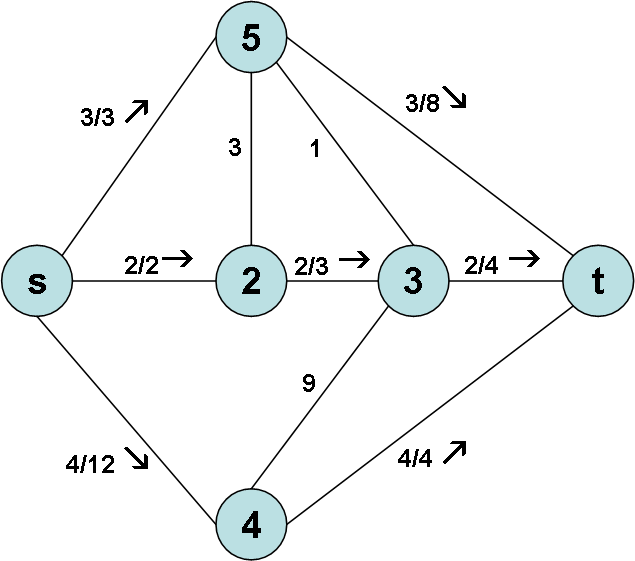
Зробимо деякі зауваження до цього алгоритму. Максимально можлива величина збільшення течії дорівнює мінімальній з пропускних здатностей ребер (в залишковій мережі), що входять до ланцюга – так зване «вузьке місце». При знаходженні цієї величини треба звертати на напрям течії та враховувати її асиметричність. На рисунку 3.17 проілюструємо приклад знаходження максимально можливої величини збільшення течії в залишковій мережі.

Рис. 3.17. Знаходження максимально можливої величини збільшення течії.

Розглянемо аргументальний ланцюг . В залишковій мережі з рисунка 3.17 пропускна здатність ребрадорівнює 3 (5-2=3); пропускна здатність ребрадорівнює 4 (4-0=4); пропускна здатність ребрадорівнює 5 (3-(-2)=5); пропускна здатність ребрадорівнює 6 (4-0=6). Таким чином, за ланцюгомми можемо збільшити течію на 3, а реброє «вузьким місцем». На рисунку 3.18 показано результат збільшення течії за ланцюгом. При цьому, якщо течія, що існувала раніше, збігається за напрямом з ребромаргументального ланцюга (,,), то ми додаємо значення течії, що існувала раніше; якщо ж течія, що існувала раніше, є протилежною за напрямом ребруаргументального ланцюга (), то ми значення течії, що існувала віднімаємо від знайденого значення збільшення течії.

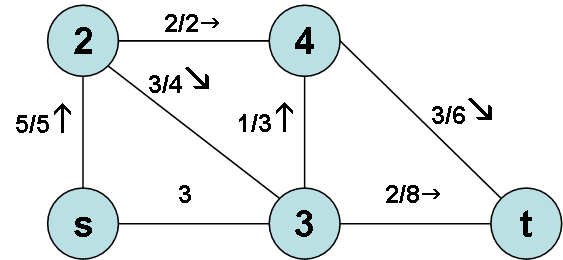
Рис. 3.18. Збільшення течії на максимально можливу величину.

Звернемо увагу, що алгоритм неконкретизує,якийсаме ланцюг мишукаємо накроці 1, або як саме ми це робимо.За цієї причини (порушення детермінованості) ця процедура формально не може називатися алгоритмом, хоча майже усі джерела з теорії графів та алгоритмів її саме так і називають.

Форд та Фалкерсон довели, що цей «алгоритм»гарантованопрацює тільки для цілих пропускних здатностей, але навіть у такому випадку при великих значеннях пропускних здатностей він може працювати дуже довго. Якщо ж пропускні здатності не є цілими числами, алгоритм може працювати нескінченно довго, не збігаючись до оптимального розв’язку. Далі наведемо приклади цих ситуацій.

На рисунку 3.19 розглянуто мережу, для якої алгоритм Форда – Фалкерсона може працювати дуже довго.

Рис. 3.19. Приклад мережі, для якої алгоритм Форда – Фалкерсона може працювати дуже довго.

Спочатку, в якості аргументального ми можемо взяти ланцюг , за яким ми можемо збільшити течію на 1. Залишкова мережа, що утворена після додавання за цим ланцюгом зображена на рисунку 3.20 (а).Далі ми можемо взяти як аргументальний ланцюг та збільшити за ним течію на 2. На рисунку 3.20 (б) зображена залишкова мережа, що утворена після другого додавання за аргументальним ланцюгом.

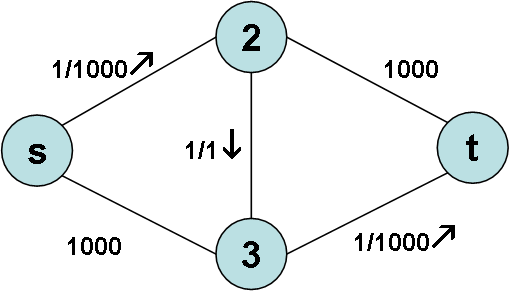
(а) (б)

Рис. 3.20. Залишкова мережа після першого (а) та другого (б) додавань течії.

Після цього, взявши як аргументальний ланцюг , за яким течія може збільшитися на 2, одержимо залишкову мережу, що зображена на рисунку 3.21 (а).Аналогічно виконуються наступні вибори аргументального ланцюга та додавання течії. На рисунку 3.21 (б) зображена залишкова мережа після 1000 додавань течії.

(а) (б)

Рис. 3.21. Залишкова мережа після третього (а) та тисячного (б) додавання течії.

Далі за ланцюгом ми можемо збільшити течію на 1 та одержимо (рис. 3.22) залишкову мережу, в якій не існуєаргументальних ланцюгів:

Рис. 3.22. Залишкова мережа після 1001 додаваня течії.

Таким чином ми знайшли максимальну течію в мережі з рисунку 3.19 після 1001 додавання течії. Сумарна величина течії дорівнює 2000. Неважко побачити, що цей самий результат можна одержати лише після двох додавань за ланцюгами (збільшення на 1000) та(збільшення на 1000). ■

На рисунку 3.23 розглянемо мережу, для якої алгоритм Форда – Фалкерсона може працювати нескінченно довго, не збігаючись до оптимального розв’язку. В цій мережі пропускна здатність ребер (2,3) та (3,4) дорівнює одиниці, пропускна здатність ребра (4,5) дорівнює числу (на рисунку позначено через, причому виконується рівність), а пропускні здатності всіх інших ребер дорівнює 10 (насправді, вони можуть дорівнювати будь-якому числу, більшому за 2).

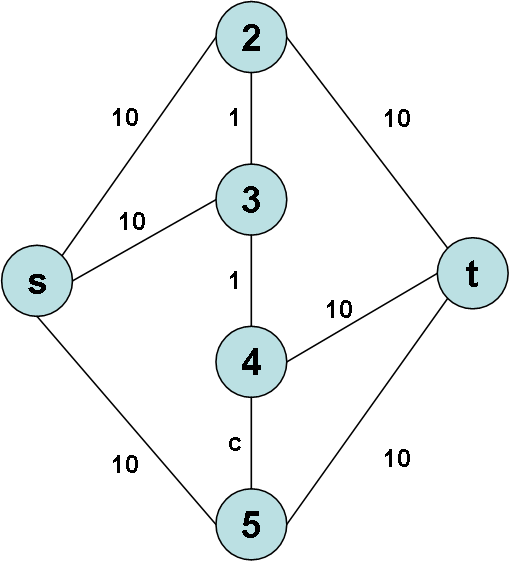
Рис. 3.23. Мережа, для якої алгоритм Форда – Фалкерсона може працювати нескінченно довго та не дати оптимального розв’язку.

Для більш стислого опису невдалої за результатом, але можливої за алгоритмом Форда – Фалкерсона, процедури додавання течії позначимо через аргументальний ланцюг, через– ланцюгта через– ланцюг.При збільшенні течії за цими ланцюгами «вузькими місцями» можуть бути лише ребра(3,2), (3,4) та (5,4). Для більшої зрозумілості наведемо у вигляді таблиці течію за цими ребрами та пропускну здатність цих ребер у залишковій мережі після кожного додавання течії. Після кожного аргументального ланцюга у дужках будемо вказувати величину збільшення течії.

Крок	Аргументальний ланцюг	Пропускна здатність ребер у залишковій мережі
		(3,2)	(3,4)	(5,4)
0
1		1	0
2				0
3			0
4		0
5			0

Таб. 3.4. Кроки виконання алгоритму Форда-Фалкерсона для мережі з рисунка 3.23.

Звернемо увагу на те, що після кроку 1 та 5 пропускна здатність ребер (3,2), (3,4) та (5,4) у залишковій мережі має значення відповідно , 0,для деякого. Можна довести, що при збільшенні течії за шляхами,,,, у нескінченній кількості разів, пропускна здатність цих ребер буде зберігатися у такому ж самому вигляді. Тому, по-перше, за таким порядком знаходження аргументальних ланцюгів алгоритм працює нескінченну кількість часу; по-друге, сумарна величина знайденої течіїдорівнює. При цьому максимальна сумарна величина течії для цієї мережі дорівнює 21. ■

Ці два приклади показали, що для алгоритму Форда – Фалкерсона потрібно чітко означити процедуру знаходження аргументальних ланцюгів. У подальшому цей алгоритм декілька разів покращували саме через відкриття нового способу знаходження аргументальних ланцюгів. Найбільш простим та відомим покращенням є алгоритм Едмонса – Карпа, який було опубліковано у 1972 році (через 17 років після відкриття алгоритму Форда – Фалкерсона). Покращення полягає у тому, що знаходимо найкоротший з аргументальних ланцюгів (за допомогою обходу в ширину). Наведемо кроки алгоритму Едмонса – Карпа.

Алгоритм 3.9. (Едмонса – Карпа) Відшукання максимальної течії в мережі.

Спочатку всі течії дорівнюють 0. Залишкова мережа співпадає з початковою мережею.

Крок 1. Знаходимо найкоротший аргументальний ланцюг у залишковій за течією мережі.

Крок 2. За ланцюгом збільшуємо течіюна максимально можливу величину, перераховуємо залишкову мережу та переходимо до кроку 1.

Алгоритм закінчує свою роботу у випадку, коли крок 1 виконати неможливо, тобто аргументального ланцюга у залишковій мережі більше не існує. Одержана таким чином течія буде максимальною. ■

Проілюструємо хід виконання алгоритму Едмонса – Карпа на наступному прикладі.

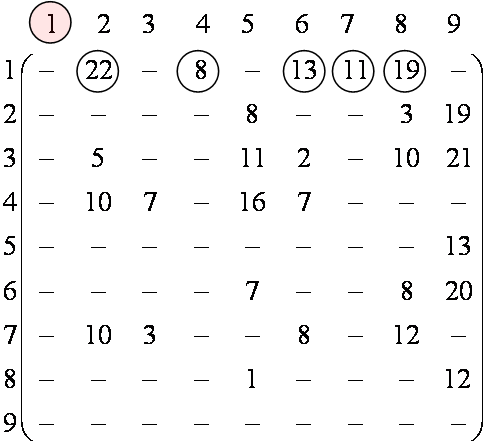
Приклад 3.11. Задано мережу , у якій, вершина 1 є джерелом, вершина 6 є стоком. Максимальну пропускну здатність ребер задано матрицею. За допомогою алгоритму Едмонса – Карпа знайти максимальну течію у мережі.

.

Для більшої наочності джерело (вершину 1) позначимо через , стік(вершину 6) – через , мережу зобразимо у вигляді діаграми, а пошукаргументальних ланцюгів та залишкову мережу після додавання течії – у таблиці 3.5.

Крок	Пошук аргументального ланцюга	Залишкова мережа
0
1
2
3
4
5
6
7	аргументального ланцюга не існує

Таб. 3.5. Кроки виконання алгоритму Едмонса-Карпа для мережі з приклада 3.11.

Оскільки на кроці 7 аргументального ланцюга не існує, то максимальною є течія, що зображена на попередньому кроці 6. Сумарна величина знайденої течії дорівнює 4+3+2+2+1+3=15. Цю течію доцільно зобразити у вигляді матриці, в якій елемент -го рядка та-го стовпцядорівнює величині течіїу випадку, коли. Якщо ж, то.

За цією матрицею зручно перевірити всі властивості течії, а саме, сума елементів першого рядка є рівною сумі елементів останнього стовпця та дорівнює сумарній величині знайденої течії; сума елементів кожного рядка, крім першого та останнього (з номером )співпадає з сумою елементів -го стовпця. ■

Далі розглянемо ще одне важливе використання графів на практиці у задачі мережевого планування.

Під час виконання проекту (будівництва споруди, виготовлення складних технічних виробів, проведення наукових експериментів та ін.) доводиться виконувати велику кількість елементарних робіт. Виконання їх пов’язане в часі: розпочати виконання робіт можна лише тоді, коли виконано усі попередні до них роботи. Інформацію про взаємозв’язок, порядок виконання та тривалість всіх робіт проекту часто подають у вигляді орієнтованого графа, який називають мережевим.

В ході реалізації проекту внаслідок виконання деяких робіт наступають певні етапи або події. Так, при будівництві споруди можна виділити такі події: завершення розробки документації; побудова фундаменту, першого та інших поверхів; побудова даху; підведення та підключення побутових комунікацій та ін. Іншими словами, подію ми будемо розуміти як результат виконання деяких робіт. Виділяють дві особливі події: початкову та завершальну, всі інші події називають проміжними. Перехід від однієї події до іншої здійснюється при виконанні відповідних робот.

У мережевому графі вершинами є події, причому початковій події відповідає вершина з номером 1, завершальній – вершина з останнім номером; ребрами є роботи, вагою ребра – тривалість відповідної роботи. Мережеві графи будемо задавати матрицею ваг. Нумерація вершин, що відповідають проміжним подіям є довільною. Можливе одночасне виконання декількох робіт. При цьому ми можемо виконувати роботи, що виходять з вершини (тобто знаходяться у -му рядку матриці ваг)лише в тому випадку, коли є виконаними всі роботи, що входять у вершину (тобто знаходяться у-му стовпці матриці ваг). Вважаємо, що подіянастає у тому випадку, коли виконані всі роботи, що входять у цю вершину, часом настання події є час завершення виконання останньої роботи у відповідну вершину. Час виконання всього проекту є часом настання завершальної події.

Мережевий граф наочно подає розгорнуту картину процесу реалізації проекту з його індивідуальними деталями і особливостями, які потрібно вміти виявляти та враховувати. Складання мережевих графів значно спрощує загальне керування проектом, а тому робить його більш ефективним. Складання мережевих графів для конкретного проекту здійснюється досвідченими фахівцями у спеціальних організаціях; розгляд цього процесу виходить за рамки нашого посібника. Звернемо увагу на основні властивості мережевих графів.

1) Не повинно бути так званих «тупікових» вершин. З кожної вершини, крім завершальної, повинна виходити хоча б одна робота.

2) Не повинно бути так званих «хвостових» вершин. У кожну вершину, крім початкову, повинна входити хоча б одна робота.

3) Не повинно бути орієнтованих циклів, оскільки при їх існуванні кожна робота з циклу не зможе розпочатися.

Для заданого мережевого графа ми будемо розв’язувати такі дві задачі:

1) Задача знаходження мінімального часу виконання всього проекту, настання кожної події та знаходження найдовших ланцюгів робіт.

2) Задача знаходження максимального часу настання кожної події, при якому весь проект буде виконано за час, що знайдено у попередній задачі.

Розв’язок першої задачі дасть нам можливість порівняти поточний процес реалізації проекту з ідеальним. Розв’язок другої задачі дозволить визначити більш важливі події, що не мають резерву часу, які потребують більшої уваги. Мінімальний час настання події будемо позначати через ; максимальний час з другої задачі (далі його будемо називати максимальним часом) – через .

Для розв’язання обох задач вершини мережевого графа треба впорядкувати за їх рангами.

Алгоритм 3.10. Знаходження рангів вершин мережевого графа.

Спочатку всі роботи не обведені, всі вершини – не помічені.

Крок 1. Ранг І присвоюємо вершині 1. Помічаємо цю вершину.

Крок 2. Обводимо всі роботи, що починаються з останньої поміченої вершини рангу (або декількох таких вершин).

Крок 3. Помічаємо всі ті вершини, в які не входить жодна необверена робота. Цим вершинам присвоюємо ранг . Якщо всі вершини графа є поміченими, то алгоритм закінчує свою роботу, у протилежному випадку переходимо до кроку 2. ■

Звернемо увагу на те, що можливість знаходження рангу кожної вершини виключає існування в мережевому графі орієнтованого циклу.

Далі перейдемо до розв’язання першої задачі.

Алгоритм 3.11. Знаходження мінімального часу виконання всіх подій та найдовших ланцюгів робіт у мережевому графі.

Спочатку всі вершини є непоміченими, час для всіх вершин дорівнює 0, шляхи є порожніми. Вершини розглядаємо за зростанням їх рангів.

Крок 1. Знаходимо непомічену вершину з найменшим рангом та помічаємо цю вершину.

Крок 2. Перераховуємо час настання усіх інших непомічених вершин за формулою. Якщо при перерахуванні час вершинизмінився, тобто її новий час дорівнює сумі часу вершинита ваги ребра, то також змінюється шлях до вершини:(під знаком + розуміємо дописування до шляхувершини). Після перерахування повертаємося до кроку 1.

Алгоритм закінчує свою роботу у випадку, коли всі вершини є поміченими, тобто крок 1 виконати неможливо. ■

Після виконання цього алгоритму ми знаходимо критичний шлях – найдовший в часі ланцюг робіт, що ведуть від початкової до завершальної події. Довжина критичного шляху (тобто, сума ваг ребер, що входять до нього) є мінімальним часом виконання всього проекту. Для того, щоб проект було виконано у строк, потрібно, щоб усі події на критичному шляху настали не пізніше запланованих строків. Затримка будь-якої події на критичному шляху призведе до затримки виконання всього проекту. Для уявлення про хід виконання проекту необхідно особливо уважно стежити за подіями на критичному шляху.

Перейдемо тепер до розв’язання другої задачі.

Алгоритм 3.12. Знаходження максимального часу виконання всіх подій,за яким час виконання всього проекту не збільшиться.

Спочатку всі вершини є непоміченими, вершини розглядаємо за спаданням їх рангів.

Крок 1. Для всіх вершин, що входять до критичного шляху, максимальний час дорівнює мінімальному. Помічаємо всі вершини, що входять до критичного шляху.

Крок 2. Знаходимо непомічену вершину найбільшого рангу та помічаємо її.

Крок 3. Перераховуємо максимальний час настання цієї вершини за формулою , деє множиною помічених вершин. Якщо всі вершини є поміченими, то алгоритм закінчує свою роботу, у протилежному випадку переходимо до кроку 2. ■

Хід виконання алгоритмів 3.10 – 3.12 зручно подавати у вигляді таблиці, яка для алгоритму 3.11 є подібною до таблиці, що ілюструє алгоритм Дейкстри (див. попередній підрозділ). Для алгоритму 3.12 після визначення максимального часу в дужках вказуємо причину обрання відповідного значення (входження до критичного шляху або номер відповідної вершини ). Покажемо хід виконанняалгоритмів 3.10 – 3.12 на наступному прикладі.

Приклад 3.12. Задано мережевий граф , у якого множина вершин, вершина 1 є початковою, а вершина 9 є завершальною. Тривалість часу між подіями задано матрицею. Знайти критичний шлях, мінімальні та максимальні строки завершення усіх подій.

.

Спочатку знайдемо ранги всіх вершин. Для більшої зручності підпишемо рядки та стовпчики матриці .

Крок	Визначені ранги вершин	Матриця з обведеними роботами та поміченими вершинами
1	І – 1
2	І – 1 ІІ – 4, 7
3	І – 1 ІІ – 4, 7 ІІІ – 3
4	І – 1 ІІ – 4, 7 ІІІ – 3 ІV – 2, 6
5	І – 1 ІІ – 4, 7 ІІІ – 3 ІV – 2, 6 V – 8
6	І – 1 ІІ – 4, 7 ІІІ – 3 ІV – 2, 6 V – 8 VІ – 5
7	І – 1 ІІ – 4, 7 ІІІ – 3 ІV – 2, 6 V – 8 VІ – 5 VІІ – 9

Таб. 3.6. Знаходження рангів вершин для мережевого графа з приклада 3.12.

Далі у таблиці 3.7 відобразимо хід виконання алгоритму 3.11.

2	3	4	5	6	7	8	9
22	15	8	24 26 30	13 15 19	11	19 23 25 27	36 41 43
1,2	1,4,3	1,4	1,4,5 1,4,3,5 1,2,5	1,6 1,4,6 1,7,6	1,7	1,8 1,7,8 1,4,3,8 1,7,6,8	1,4,3,9 1,2,9 1,2,5,9

Таб. 3.7. Ілюстрація виконання алгоритму 3.11.

Таким чином, мінімальний час настання події 2 дорівнює 22, ,,,,,,, тобто в оптимальному випадку проект буде завершено через 43 одиниці часу. Критичний шлях проекту – 1, 2, 5, 9.

Тепер ми можемо виконувати алгоритм 3.12. Результат виконання цього алгоритму покажемо у таблиці 3.8.

2	3	4	5	6	7	8	9
22	15	8	24 26 30	13 15 19	11	19 23 25 27	36 41 43
1,2	1,4,3	1,4	1,4,5 1,4,3,5 1,2,5	1,6 1,4,6 1,7,6	1,7	1,8 1,7,8 1,4,3,8 1,7,6,8	1,4,3,9 1,2,9 1,2,5,9
22 (КШ)	17 (2)	10 (3)	30 (КШ)	21 (8)	12 (2)	29 (5)	43 (КШ)

Таб. 3.8. Результат виконання алгоритму 3.12.

Зробимо деякі коментарі до виконання алгоритму 3.12.