Математическая_Статистика_КР8

27

6.Проверка статистических гипотез

Статистической гипотезой называется предположение о виде неизвестного распределения случайной величины или о параметрах известного распределения.

Примером статистических гипотез являются следующие высказывания: генеральная совокупность, о которой мы располагаем лишь выборочными сведениями, имеет нормальный закон распределения или генеральная средняя (математическое ожидание случайной величины) равна 5.

Не располагая сведениями о всей генеральной совокупности, высказанную гипотезу сопоставляют, по определенным правилам, с выборочными сведениями и делают вывод о том, можно принять гипотезу или нет. Процедура сопоставления высказанной гипотезы с выборочными данными называется проверкой гипо-

тезы.

Располагая выборочными данными x1, x2 ,..., xnи руководствуясь конкрет-

ными условиями рассматриваемой задачи, формулируют гипотезу Н0, которую называют основной или нулевой, и гипотезу H1, конкурирующей с гипотезой Н0.

Термин «конкурирующая» означает, что являются противоположными следующие два события:

по выборке будет принято решение о справедливости для генеральной совокупности гипотезы Н0;

по выборке будет принято решение о справедливости для генеральной совокупности гипотезы Н1.

Гипотезу Н1 называют также альтернативной.

Гипотеза Н0 называется простой, если она полностью определяет теоретическое распределение случайной величины по имеющейся выборке ее значений. В противном случае гипотеза называется сложной.

Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез.

		Суть проверки статистических гипотезы заключается в том, что использует-
ся	специально						составленная выборочная	характеристика (статистика)
~	(x ,	x	2	, ...,	x	n	) , полученная по выборке x , x ,..., x		n	, имеющая известный за-
n	1						1 2

табулированный закон распределения. Значения этого закона позволяют судить о «расхождении выборки с гипотезой Н0».

~n называется статистическим критерием. Множество ее возможных зна-

чений разбивается на два непересекающихся подмножества: одно из них (критическая область) содержит значения критерия, при которых нулевая гипотеза от-

клоняется, второе (область принятия гипотезы) – значения ~n , при которых она

28

принимается. Значения ~n , отделяющие критическую область от области принятия гипотезы, называются критическими точками кр .

Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным, т.е. по ограниченному ряду наблюдений; следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов:

отвергают гипотезу Н0, или, иначе, принимают альтернативную гипотезу Н1, тогда как на самом деле гипотеза Н0 верна; это ошибка первого рода;

принимают гипотезу Н0, тогда как на самом деле высказывание Н0 неверно, т.е. верной является гипотеза Н1; это ошибка второго рода.

Уровнем значимости α называют вероятность ошибки первого рода:

α PH0 (H1),

(6.1)

где PH 0 (H1) – вероятность того, что будет принята гипотеза Н1, если на самом деле в генеральной совокупности верна гипотеза Н0.

Вероятность задается заранее, разумеется, малым числом, поскольку это вероятность ошибочного заключения, при этом обычно используют некоторые стандартные значения: 0,05; 0,01; 0,005; 0,001.

Например, α = 0,05 означает следующее: если гипотезу Н0 проверять по каждой из 100 выборок одинакового объема, то в среднем в 5 случаях из 100 мы совершим ошибку первого рода.

Вероятность ошибки второго рода обозначают β :
β PH (H0 ),	(6.2)
1

где PH1 (H0 ) – вероятность того, что будет принята гипотеза Н0, если на самом деле верна гипотеза Н1.

Обратим внимание на то, что в результате проверки гипотезы относительно гипотезы Н0 может быть принято и правильное решение. Существует правильное решение двух следующих видов:

принимают гипотезу Н0, тогда как и в действительности, в генеральной совокупности, она имеет место; вероятность этого решения PH0 (H0 ) 1 α;

не принимают гипотезу Н0 (т. е. принимают гипотезу Н1), тогда как и на самом деле гипотеза Н0 неверна (т.е. верна гипотеза Н1); вероятность этого решения

PH1 (H1) 1 .

Величину 1 , т.е. вероятность недопущения ошибки первого рода, называется мощностью критерия.

Последствия ошибок первого и второго рода могут быть совершенно различными: в одних случаях надо минимизировать , в другом — β . Так, приме-

нительно к радиолокации говорят, что — вероятность пропуска сигнала, β —

29

вероятность ложной тревоги; применительно к производству, к торговле можно сказать, что — риск поставщика (т.е. забраковка по выборке всей партии изделий, удовлетворяющих стандарту), β — риск потребителя (т.е. прием по выборке

всей партии изделий, не удовлетворяющей стандарту); применительно к суебной системе, ошибка первого рода приводит к оправданию виновного, ошибка второго рода — осуждению невиновного.

Порядок проверки статистической гипотезы таков.

1)Располагая выборочными данными x1, x2 ,..., xnи руководствуясь конкрет-

ными условиями рассматриваемой задачи, формулируют основную гипотезу Н0 и альтернативную гипотезу Н1.

2)Выбирается статистический критерий ~n .

3)	По статистике	~	и уровню значимости	определяется вид критической
		n

области. Для ее отыскания достаточно найти (обычно по таблицам для закона распределения ~n ) значение критической точки, т.е. границу, отделяющую критическую область от области принятия гипотезы. кр .

	Возможны три вида расположения критической области (в зависимости от
вида нулевой и альтернативной гипотез, вида и распределения критерия						~n ):
	правосторонняя		критическая		область, состоящая из	интервала
(	кр	) , где точка	кр
	пр,α ,		пр,α определяется из условия
			P(	~	пркр,α. ) α	(6.3)
				n

и называется правосторонней критической точкой, отвечающей уровню значимости α;

левосторонняя критическая область, состоящая из интервала (					,	кр.
						лев,α ) .
где точка	кр.	определяется из условия
	лев,α
		P(	~	кр.	(6.4)
			n	лев,α ) α

и называется левосторонней критической точкой, отвечающей уровню значимости α;

двусторонняя критическая область, состоящая из следующих двух интер-

		кр.		кр				кр.		кр
валов: ( ,		лев,α / 2 )		и ( пр,α / 2 ,		) , где точки		лев,α / 2	и	пр,α / 2	определяются
из условий
		P(	~	кр.	и	P(	~	кр.			(6.5)
			n	лев,α / 2 ) α/2			n	пр,α / 2 )	α/2
и называются двусторонними критическими точками.
4)	по выборке вычисляется наблюдаемое значение критерия набл ;

				30
5) если	набл	попадает в критическую область, нулевая гипотеза отвергается;
при попадании			набл	в область принятия гипотезы нулевая гипотеза прини-

мается.

Рассмотрим способы проверки некоторых статистических гипотез.

6.1. Сравнение двух дисперсий нормальных генеральных совокупностей

Гипотезы о дисперсиях возникают довольно часто, так как дисперсия характеризует такие исключительно важные показатели, как точность машин, приборов технологических процессов, степень однородности совокупностей, риск, связанный с отклонением доходности активов от ожидаемого уровня и т.д.

Пусть имеются две выборки объемов п1 и п2, извлеченные из нормально распределенных генеральных совокупностей Х и Y. Требуется по исправленным

выборочным дисперсиям sx2 и s2y проверить нулевую гипотезу о равенстве генеральных дисперсий рассматриваемых генеральных совокупностей:

Ho: D (X) = D (Y).

(6.6)

Критерием служит случайная величина

s2

F б (6.7)

sм2

– отношение большей исправленной дисперсии к меньшей, которая при условии справедливости нулевой гипотезы имеет распределение Фишера со степенями свободы k1 = n1 – 1 и k2 = n2 – 1 (n1 — объем выборки, имеющей большую исправленную дисперсию, соответственно n2 —меньшую). Критическая область зависит от вида конкурирующей гипотезы:

1) если H1: D (X) > D (Y), то критическая область правосторонняя:

p(F Fкр ( , k1, k2 )) .

Критическая точка Fкр ( , k1, k2 ) находится по таблице критических точек

распределения Фишера (см. приложение 3).

Если Fнабл

sб2

Fкр

нулевая гипотеза принимается, в противном случае

sм2

– отвергается.

2) При конкурирующей гипотезе H1: D (X) ≠ D (Y) критическая область двусто-

ронняя:

p(F F1)

,

p(F

F2 )

.

При этом

необходимо

найти

2

2

Fкр.прав.

Fкр (

, k1, k2 )

и

Fкр, лев.

1/ Fкр (

, k2 , k1 ) .

Тогда,

если

2

2

				31
		s2
	Fнабл	б	[Fкр,лев.; Fкр,прав.]	нет оснований отвергнуть нулевую гипотезу, в про-
		sм2

тивном случае нулевую гипотезу отвергают.

Пример 6.1. Даны две независимые выборки объемов п1 = 10 и п2 = 15, извлеченные из генеральных совокупностей Х и Y (расход сырья по старой и новой технологии), распределенных по нормальному закону. Найдены исправленные выбо-

рочные дисперсии sx2 2,67 и s2y 1,88. Проверим при уровне значимости α = 0,05

нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипо-

тезе H1: D (X) > D (Y).

Решение.

Основная гипотеза Ho: D (X) = D (Y). Конкурирующая гипотеза H1: D (X) > D (Y).

Найдем значение Fкр (0,05; 9; 14) 2,65 по таблице (см. приложение 3). Критическая область – правосторонняя. Вычислим наблюдаемое значение крите-

2,67

рия: Fнабл 1,88 1,42 Fкр.

Следовательно, нет оснований отвергнуть нулевую гипотезу. ►

6.2. Сравнение двух средних генеральных совокупностей

Сравнение средних двух совокупностей имеет важное практическое значение. На практике часто встречается случай, когда средний результат одной серии экспериментов отличается от среднего результата другой серии. При этом возникает вопрос, можно ли объяснять обнаруженное расхождение средних неизбежными случайными ошибками эксперимента или оно вызвано другими причинами.

Задача сравнения средних часто возникает при выборочном контроле качества изделий, изготовленных на разных установках или при различных технологических режимах, в финансовом анализе – при сопоставлении уровня доходности различных активов и т.д.

1) Генеральные совокупности Х и Y распределены нормально, причем известны их дисперсии. Из этих генеральных совокупностей извлечены выборки объемов со-

ответственно т и п, для которых найдены выборочные средние х и у . При за-

данном уровне значимости α проверяется нулевая гипотеза о равенстве математических ожиданий генеральных совокупностей:

Но: М (Х) = М (Y).

(6.8)

Статистическим критерием для проверки этой гипотезы является нормированная нормально распределенная случайная величина

32

Z

M ( X ) M (Y )

.

(6.9)

D( X ) D(Y )

m

n

Наблюдаемое значение критерия

zнабл

x

y

. Вид критической

D( X )

D(Y )

m n

области зависит от типа конкурирующей гипотезы:

а) Н1: М (Х) ≠ М (Y) – критическая область двусторонняя, zкр определяется как аргумент функции Лапласа, при котором Ф0 (zкр ) (1 )2, и критическая область

задается неравенством |Z| > zкр.

б) Н1: М (Х) > М (Y) – критическая область правосторонняя, zкр определяется как аргумент функции Лапласа, при котором Ф0 (zкр ) (1 2 )2, и критическая об-

ласть определяется неравенством Z > zкр.

в) Н1: М (Х) < М (Y) – критическая область левосторонняя, заданная неравенством Z < -zкр, где zкр вычисляется так же, как в предыдущем случае.

2) Имеются две независимые выборки большого объема, извлеченные из генеральных совокупностей, законы распределения и дисперсии которых неизвестны. При этом для объема выборки, не меньшего 30, можно считать, что выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий (следовательно, считаем известными приближенные значения генеральных дисперсий). Тогда задача сводится к предыдущей, и статистический критерий имеет вид:

								(6.10)
Z Z	X			Y			.
	D ( X )				D (Y )

m n

Наблюдаемое значение критерия вычисляется по формуле

zнабл		x y					.	(6.11)
		D( X ) D(Y )
		m			n

При этом выбор вида критической области и определение критических точек проводятся так же, как в пункте 1.

3) Генеральные совокупности распределены нормально, причем их дисперсии неизвестны, а объем выборок т и п мал (следовательно, нельзя получить хорошие оценки генеральных дисперсий). Если предположить, что генеральные дисперсии равны, то в качестве критерия для проверки нулевой гипотезы Но: М (Х) = М (Y) служит случайная величина

прав.кр.

33

(6.12)

X

Y

nm(n

m 2)

t

,

n

m

2

(n

2

(m 1)sx

1)sy

имеющая при

справедливости

нулевой

гипотезы

распределение Стьюдента с

k = n + m – 2 степенями свободы. Наблюдаемое значение критерия вычисляется по формуле

			х	у					nm(n	(6.13)
tнабл										m 2)	.
									n
			2		2
		(m		(n						m
			1)sx		1)sy

Критическая область строится в зависимости от вида конкурирующей гипотезы.

а) Н1: М (Х) ≠ М (Y) – критическая область двусторонняя, задаваемая неравенст-

вом |t| > tдвуст.кр., где tдвуст.кр.(α, k) находится из таблицы критических точек распределения Стьюдента.

б) Н1: М (Х) > М (Y) – критическая область правосторонняя, определяемая условием t > t . Критическая точка tправ.кр.(2α, k)вновь находится по таблице критических точек распределения Стьюдента.

в) Н1: М (Х) < М (Y) – критическая область левосторонняя, t < – tправ.кр..

Пример 6.2. Имеются независимые выборки значений нормально распределенных случайных величин, характеризующих производительность без применения новых технологий и с применением новых технологий соответственно

Х: 2, 2, 3, 3, 4, 4, 4, 5, 5, 6

и

Y: 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 7, 8, 9.

Требуется проверить для уровня значимости α = 0,1 при условии равенства генеральных дисперсий нулевую гипотезу Н0: М (Х) = М (Y) при конкурирующей гипотезе Н1: М (Х) ≠ М (Y). Нулевая гипотеза: средняя выработка одинакова при старой и новой технологии.

Решение.

Объемы выборок т = 10, п = 15. Вычислим выборочные средние и исправленные

выборочные дисперсии: x	3,8; y 4,93;			sx2	1,73;		s2y 3,21. Вычислим наблю-
даемое значение критерия:	tнабл		3,8	4,93			10 15			23		1,706.	Критиче-
							25
			9 1,73	14	3,21

ская область – двусторонняя, tдвуст.кр.(0,1; 23) = 1,71. Итак, |tнабл | < tдвуст.кр., следовательно, нет оснований отвергнуть нулевую гипотезу – можно считать, что мате-

матические ожидания генеральных совокупностей равны.

Т.е. мы получили, что новая технология никак не повлияла на производительность. Но нужно помнить, что принятие основной гипотезы не означает, что она безоговорочно верна. Вполне возможно, что только незначительный объем выборки позволил принять нулевую гипотезу, а при увеличении объемов выборок нулевая гипотеза будет отвергнута.►

34

6.3. Сравнение двух вероятностей биномиальных распределений

Пусть известны результаты двух серий независимых испытаний: в первой серии проведено п1 опытов, и событие А появилось т1 раз; во второй серии из п2 опытов событие А появилось т2 раз. Обозначим неизвестную вероятность появления события А в одном опыте первой серии через р1, а во второй серии – через р2. Требуется проверить при уровне значимости α нулевую гипотезу о равенстве этих вероятностей: Но: р1 = р2.

В качестве критерия выбирается нормированная нормально распределенная случайная величина

M1

M 2

U

n1

n2

.

(6.14)

p(1 p)

1

1

n1

n2

Наблюдаемое значение критерия вычисляется по формуле:

m1

m2

U

n1

n2

.

(6.15)

набл

m2

m1

m2

m1

1

1

1

n1

n2

n1

n2

n1

n2

Построение критической области:

а) при конкурирующей гипотезе

Н1:

р1 ≠

р2 uкр

определяется из равенства

Ф0 (икр ) (1 )

2 , и двусторонняя критическая область задается неравенством

|U| > uкр.

б) при конкурирующей гипотезе Н1: р1 > р2 uкр для правосторонней критической

области находится из условия Ф0 (икр ) (1	2 ) 2, и вид критической области:
U > uкр.
в) при конкурирующей гипотезе Но: р1 < р2	левосторонняя критическая область

имеет вид U < – uкр, где uкр находится по формуле из пункта б).

Пример 6.3. В серии из 20 независимых испытаний (20 студентов одной группы сдают экзамен) событие А (экзамен сдан на отлично) появилось 8 раз, в серии из 15 испытаний (15 студентов другой группы сдают экзамен) – 7 раз. При уровне значимости α = 0,05 проверяется

нулевая гипотеза Но: р1 = р2 при конкурирующей гипотезе Но: р1 < р2. (отсутствие существенных различий в усвоении учебного материала).

Решение.

								35
	Критическая							область – левосторонняя, Ф0 (икр ) (1 2 0,05) 2 0,45, следова-
	тельно, икр=1,645, и критическая область имеет вид U<-1,645. Вычислим инабл=
				8		7
				20		15				0,394. Uнабл > – uкр, следовательно, гипотеза принимается,
	15			20		1		1

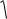35 35 20 15

и можно считать, что вероятность события А в обеих сериях испытаний одинакова, т.е. гипотеза об одинаковом уровне усвоения учебного материала студентами групп не противоречива. ►

6.4. Проверка гипотез о числовых значениях параметров

Задачи, рассмотренные в этом разделе могут возникать, например, в финансовом анализе, когда по данным выборки надо установить, можно ли считать доходность актива определенного типа или портфеля ценных бумаг, либо ее риск равным заданному числу; или по результатам выборочной аудиторской проверки однотипных документов нужно убедиться, можно ли считать процент допущенных ошибок равным номиналу, и т.п.

Рассмотрим проверку гипотез о числовых значениях параметров нормального закона распределения. Соответствующие критерии проверки гипотез о числовых значениях параметров нормального распределения приведены в таблице 4.

Нулевая ги-

Предположения

Статистика

Альтернативная

Критерий от-

потеза

критерия

гипотеза

клонения ги-

потезы

a

a0

2 известна

t

x

a0

a

a1

a0

| t |

t1 2

n

a

a1

a0

a

a1

a0

| t |

t1

a

a0

2 неизвестна

t

x

a0

a

a1

a0

| t |

t(2

, n

1)

s

n

1

a

a1

a0

| t |

t(

, n

1)

a

a1

a0

Здесь t1 2

определяется из условия 0 (t1 2

)

(1 2

) 2 (

0 (t) — нормирован-

ная функция Лапласа), t( , n 1) находится из таблицы критических точек распределения Стьюдента.

Пример 6.4. На основании сделанного прогноза средняя дебиторская задолженность однотипных предприятий региона должна составить a0 120 ден.ед. Выбо-

рочная проверка 10 предприятий дала среднюю задолженность 135 ден.ед., а среднее квадратическое отклонение задолженности 20 ден. ед. На уровне значимости 0,05 выяснить, можно ли принять данный прогноз.

36

Решение.

Основная гипотеза H 0 : a a0 120 .

Альтернативная гипотеза H1 : a a0 .

Так как генеральная дисперсия неизвестна, то используем t-критерий Стью-

	дента. В соответствии с таблицей 4	t	x		a0			135	120				2,25 .
			s n 1					20	10		1
	Критическое значение статистики tкр				t(2			0,05;9)			t(0,1;9) 1,83.

Так как | t | tкр , гипотеза H 0 отвергается, т.е. данный прогноз не принима-

ем. ►

6.5. Критерий согласия Пирсона

Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытному распределению, представляющему вариационный ряд.

Для решения этой задачи необходимо определить вид и параметры закона распределения.

Предположение о виде закона распределения может быть выдвинуто исходя из теоретических предпосылок, опыта аналогичных предшествующих исследований, на основании графического изображения эмпирического распределения и т.д.

Параметры распределения, как правило не известны, поэтому их заменяют наилучшими оценками по выборке.

Как бы хорошо не был подобран теоретический закон распределения, между теоретическим и эмпирическим законом распределения неизбежны расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связанными с тем, что теоретический закон распределения подобран неудачно.

Для ответа на этот вопрос и служат критерии согласия.

Критерием согласия называется критерий проверки гипотезы о предпола-

гаемом законе неизвестного распределения.
Наиболее часто используется на практике критерий					2 -Пирсона.
Пусть по выборке объема n получено эмпирическое распределение:
Варианты	x1		x2		...		x
Частоты	n1		n2		...		n