
- •Федеральное агентство по образованию
- •Цель работы: исследование проводимости полупроводников с собственной и примесной проводимостью.
- •1.Краткие теоретические сведения
- •1.1. Зонная теория твердого тела
- •1.1.1. Уравнение шредингера для твердого тела
- •1.1.2. Одноэлектронное приближение
- •1.1.3. Функции блоха
- •1.1.4. Свойства волнового вектора электронов в кристалле. Зоны бриллюэна
- •1.1.5. Энергетический спектр электронов в кристалле. Модель кронига-пенни
- •1.1.6. Заполнение зон электронами. Металлы, диэлектрики, полупроводники
- •1.1.7. Эффективная масса электрона
- •1.2. Электрические свойства полупроводников
- •2.1.1.Энергетические уровни примесных атомов в кристалле
- •2.1.2. Собственная проводимость полупроводников
- •2.1.3.Электропроводность примесных полупроводников
- •2.1.4.Элементарная теория электропроводности полупроводников
- •1.2.5.Статистика электронов и дырок в полупроводниках
- •1.2.5.1.Плотность квантовых состояний
- •1.2.5.2.Функция распределения ферми-дирака
- •1.2.5.3.Степень заполнения примесных уровней
- •1.2.5.4.Концентрация электронов и дырок в зонах
- •1.2.6.Зависимость проводимости полупроводника от температуры
- •2.Методика эксперимента и экспериментальная установка
- •3. Порядок выполнения исследований
- •4. Требования к оформлению отчета
- •5. Контрольные вопросы
- •Примечание
- •Раздел 1 теоретических сведений предназначен только для студентов фрэи, для студентов других специальностей – на усмотрение преподавателя.
- •6.Список литературы
1.1.2. Одноэлектронное приближение
Многоэлектронная
задача (решение уравнения (1.1.2)) может
быть сведена к одноэлектронной. Для
этого используют метод Харти-Фока,
который состоит в замене потенциальной
энергии взаимодействия электронов в
уравнении (1.1.2) потенциальной энергией
вида
![]() ,
представляющей собой энергию взаимодействияi-го
электрона с некоторым эффективным
полем, в котором каждый электрон движется
независимо. Это поле характеризует
действие всех остальных электронов на
i
– ый электрон. Тогда уравнение Шредингера
принимает вид:
,
представляющей собой энергию взаимодействияi-го
электрона с некоторым эффективным
полем, в котором каждый электрон движется
независимо. Это поле характеризует
действие всех остальных электронов на
i
– ый электрон. Тогда уравнение Шредингера
принимает вид:
![]() ,
(1.1.3)
,
(1.1.3)
то есть гамильтониан системы представляет теперь сумму гамильтонианов отдельных электронов.
Решением (1.1.3) является функция
![]() .
(1.1.4)
.
(1.1.4)
Каждая
![]() удовлетворяет одноэлектронному уравнению
Шредингера
удовлетворяет одноэлектронному уравнению
Шредингера![]() ,
в котором взаимодействиеi-го
электрона с остальными описывается
потенциалом
,
в котором взаимодействиеi-го
электрона с остальными описывается
потенциалом
![]() .
.
Таким
образом, введение эффективного поля
позволяет свести многоэлектронное
уравнение к системе одноэлектронных.
При этом энергия системы
![]() .Функция
(1.1.4) является решением уравнения
Шредингера для кристалла, однако не
удовлетворяет принципу Паули.
.Функция
(1.1.4) является решением уравнения
Шредингера для кристалла, однако не
удовлетворяет принципу Паули.
Согласно
принципу Паули, в одном квантовом
состоянии, характеризуемом волновой
функцией
![]() ,
не может находиться более двух электронов
с разной ориентацией спинов. Удовлетворяющая
этому условию полная волновая функция
системы должна быть антисимметричной,
то есть менять знак при перемене местами
двух электронов. Эту функцию записывают
в виде определителя Слэтера:
,
не может находиться более двух электронов
с разной ориентацией спинов. Удовлетворяющая
этому условию полная волновая функция
системы должна быть антисимметричной,
то есть менять знак при перемене местами
двух электронов. Эту функцию записывают
в виде определителя Слэтера:
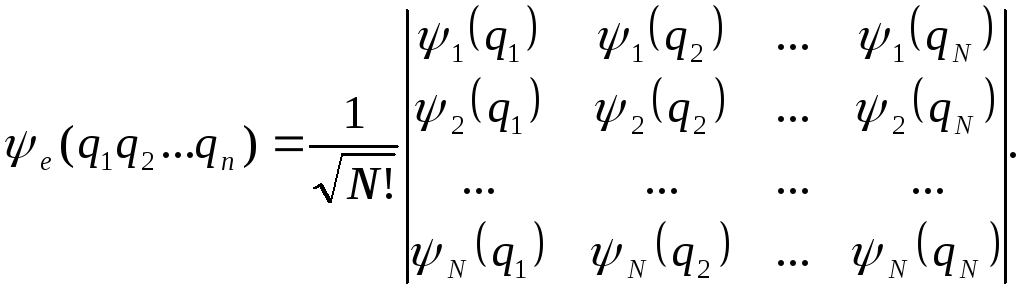
Здесь
N
-число
электронов, q
обозначает набор трех пространственных
координат и проекций спина, множитель
![]() обеспечивает нормировку функции
обеспечивает нормировку функции![]() .
Антисимметричные свойства вытекают из
свойств определителя.
.
Антисимметричные свойства вытекают из
свойств определителя.
Обозначим
потенциальную энергию электрона в
кристалле
![]() и запишем уравнение Шредингера в виде
и запишем уравнение Шредингера в виде
![]() .
.
Атомы в кристалле расположены строго периодически, поэтому полный потенциал кристалла должен обладать трехмерной периодичностью.
1.1.3. Функции блоха
Блохом было доказано, что волновые функции, являющиеся решениями одноэлектронного уравнения Шредингера с периодическим потенциалом, имеющим период решетки, представляют собой плоские волны, модулированные некоторой функцией с периодичностью решетки:
![]() .
(1.1.5)
.
(1.1.5)
Здесь
![]() - некоторая периодическая функция с
периодом, равным периоду решетки,
зависящая от волнового вектора
- некоторая периодическая функция с
периодом, равным периоду решетки,
зависящая от волнового вектора![]() .
.
Условия
периодичности потенциальной энергии
в кристалле
![]() ,
где
,
где![]() ,
где
,
где![]() – векторы единичных трансляций,
– векторы единичных трансляций,![]() -
произвольные целые числа. При смещении
кристалла на
-
произвольные целые числа. При смещении
кристалла на![]() ,
он совмещается сам с собой. Из условия
трансляционной симметрии следует, что
волновая функция электрона
,
он совмещается сам с собой. Из условия
трансляционной симметрии следует, что
волновая функция электрона![]() отличается от волновой функции
отличается от волновой функции![]() некоторым
постоянным множителем
некоторым
постоянным множителем
![]() .
(1.1.6)
.
(1.1.6)
Из
условия нормировки
![]() ,
Это условие можно удовлетворить, положив
,
Это условие можно удовлетворить, положив![]() ,
где
,
где![]() - волновой вектор, характеризующий
квантовое состояние электрона в
кристалле. Тогда из выражения (1.1.6)
получаем:
- волновой вектор, характеризующий
квантовое состояние электрона в
кристалле. Тогда из выражения (1.1.6)
получаем:
![]() ,
,
или
![]() ,
,
где
![]() .
Таким образом, волновая функция электрона
в кристалле представляет собой бегущую
волну
.
Таким образом, волновая функция электрона
в кристалле представляет собой бегущую
волну![]() ,
модулированную периодической функцией
,
модулированную периодической функцией![]() ,
имеющей период решетки и зависящей от
волнового вектора
,
имеющей период решетки и зависящей от
волнового вектора![]() .
Функция
.
Функция![]() ,
определяемая уравнением (1.1.5), называется
функцией Блоха.
,
определяемая уравнением (1.1.5), называется
функцией Блоха.
