
статика / GLAVA2
.docГлава 2. Система сходящихся сил
2.1. Приведение системы сходящихся сил
к равнодействующей
2.1.1. Векторная (геометрическая) форма
Пусть имеется
система, например, четырех сходящихся
сил
![]() ,
действующих на НМС (МТ) (рис. 13).
,
действующих на НМС (МТ) (рис. 13).
На основании следствия из аксиомы 2 перенесем силы вдоль линии их действия в точку пересечения этих линий, и последовательно сложив все силы по правилу треугольника, получим силовой многоугольник (рис. 13).
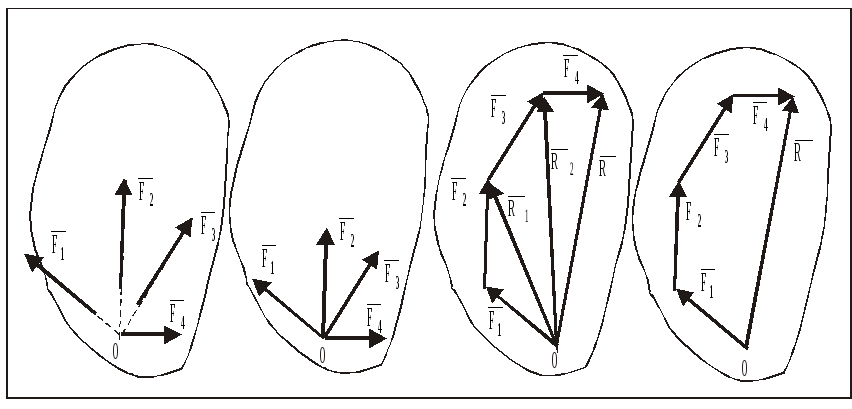 Рис.
13
Рис.
13

Таким образом, можно записать:
![]() или
или
![]() .
.
Аналогично для системы n сходящихся сил, получим:
![]() .
(2.1)
.
(2.1)
Система сходящихся сил всегда приводится к одной силе – равнодействующей этой системы сил, которая является замыкающей стороной силового многоугольника, построенного на этих силах, и равна геометрической сумме этих сил.
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской - плоской фигурой.
2.1.2. Алгебраическая форма
Выбрав декартовую систему координат с началом в точке пересечения линий действия сил и спроектировав соотношение (2.1) на ее оси, получим проекции равнодействующей пространственной системы сходящихся сил на эти оси:
![]() (2.2)
(2.2)
Модуль равнодействующей определяется соотношением:
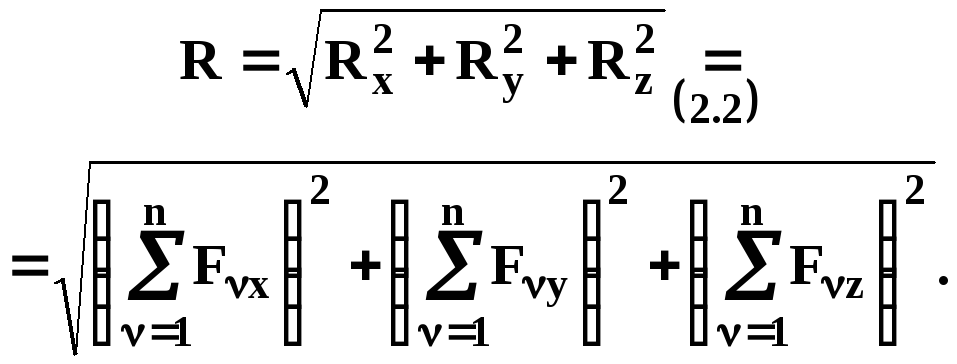 (2.3)
(2.3)
Направление равнодействующей определяется направляющими косинусами:
![]() (2.4)
(2.4)
Для плоской системы
сходящихся сил в соотношениях (2.2)–(2.4)
![]() ,
если плоская система сил находится в
плоскости xОy.
,
если плоская система сил находится в
плоскости xОy.
2.2. Условия равновесия системы сходящихся сил
2.2.1. Векторная (геометрическая) форма
Для равновесия системы сходящихся сил, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут или, другими словами, ее равнодействующая была равна нулю:
![]() .
(2.5)
.
(2.5)
2.2.2. Алгебраическая форма
Для равновесия пространственной системы сходящихся сил, необходимо и достаточно, чтобы суммы проекций сил на оси декартовой системы координат были равны нулю:
![]() (2.6)
(2.6)
В случае плоской системы сходящихся сил, находящейся в плоскости хОу, условий равновесия будет два:
![]() (2.7)
(2.7)
2.2.3. Теорема о трех уравновешенных силах
При решении задач полезно иметь в виду следующую теорему о трех силах.
Теорема: Если плоская система трех непараллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.
Доказательство:
Пусть имеется система трех сил (![]() ),
отвечающая условиям теоремы. На основании
следствия из аксиомы 2 силы
),
отвечающая условиям теоремы. На основании
следствия из аксиомы 2 силы
![]() и
и
![]() переносятся вдоль линий действия в
точку их пересечения, а на основании
аксиомы 3 они заменяются равнодействующей
(рис. 14):
переносятся вдоль линий действия в
точку их пересечения, а на основании
аксиомы 3 они заменяются равнодействующей
(рис. 14):
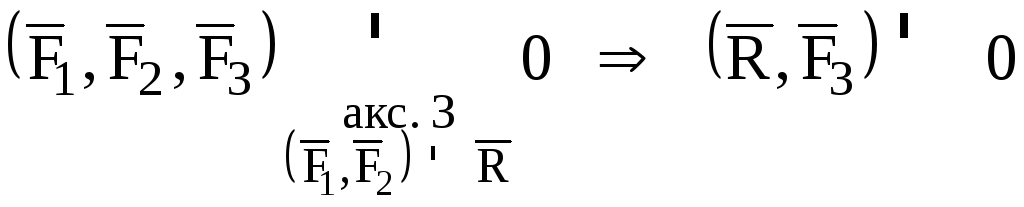 .
.
На основании
аксиомы 1 вектора
![]() и
и
![]() лежат на
одной прямой, т.е. линии действия силы
лежат на
одной прямой, т.е. линии действия силы
![]() должна проходить через точку О.
должна проходить через точку О.
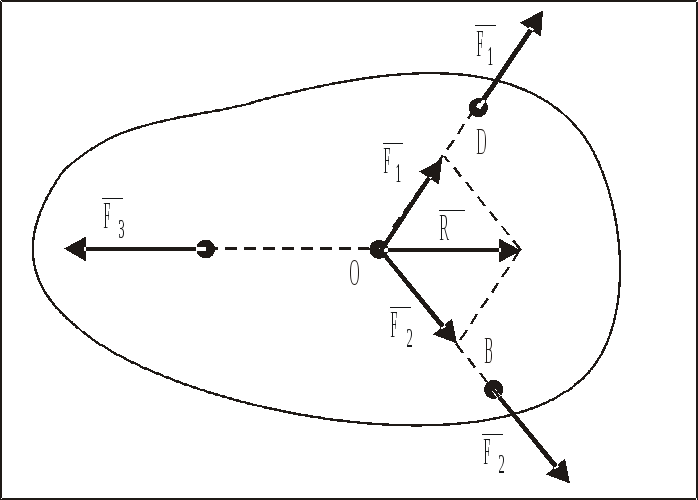
Рис. 14.
