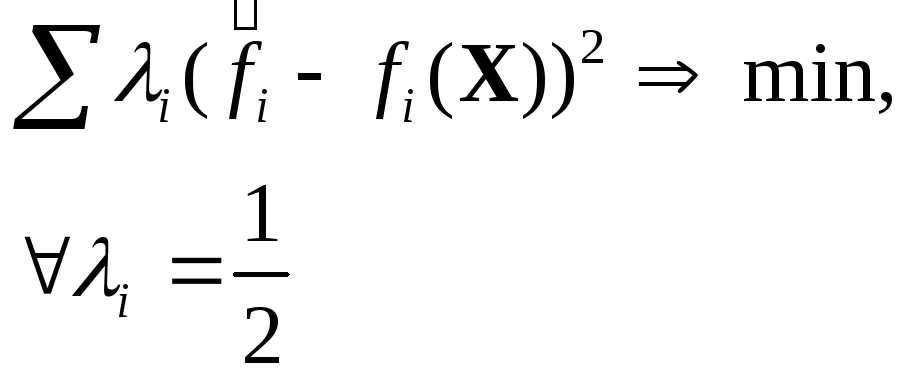10.2.1.5. Максиминная свертка

Как и в предыдущем подходе, ЛПР должен задать веса C_iвсем критериям, но обобщенный критерий записывается в виде

F(X)=.(10.I8)

Тогда многокритериальная задача сводится к максимизации F(X) на ХD. Если ввести новую переменнуюх_о, то эта задача преобразуется к виду

F(Х)=х_о max;

х_о, i=;(10.19)

XD,

который более удобен для решения. В частности, если в исходной задаче все функции линейны, то и задача в виде (10.19) будет обычной задачей линейного программирования.

Функция (10.18) подпадает под действие теоремы 5, что гарантирует получение, по крайней мере, слабо эффективного решения многокритериальной задачи.

Максиминная свертка имеет те же недостатки, что и предыдущая, но отличается тем, что максимально увеличивает минимальное слагаемое в (10.17), способствуя относительному сближению значений критериев.

Пример 10.2. Применим рассмотренный подход к задаче из примера 10.1. Снова возьмем равные веса. В соответствии с (10.19) к исходным условиям задачи добавятся ограничения

-3x₁+2x₂3x₀

4x₁+3x₂3x₀

2x₁-5x₂3x₀

и новый критерий х₀ max. Оптимальное решение этой задачи достигается в точкех=х=х=0, в которойf₁, f₂ иf₃тоже равны нулю.

Сравним с результатами примера 10.1. При решении по критерию (10.17) получили f_i=-15, а по критерию (10.18) f_i=0. Однако это решение доставляет наихудшее значение критериюf₂и ни одному из критериев не обеспечивает максимального значения.

10.2.1.6. Метод идеальной точки

Идеальной или точкой абсолютного максимума называют точку в критериальном пространстве, в которой все критерии достигают своих максимальных значений: .

Е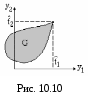сли эта точка принадлежит достижимому множествуG,то все эффективное (паретовское) множество состоит из этой единственной точки (рис. 10.10) и проблемы как таковой в этом случае нет. Однако идеальная точка обычно лежит вне множестваGи поэтому нереализуема. В связи с этим ее иногда называют также утопической. Идея метода состоит в том, чтобы на множествеGнайти точку, наиболее близкую к идеальной. Мерой близости выступает некоторая функция расстояния , в качестве которой используют в общем случае взвешенныеL_p-метрики

,

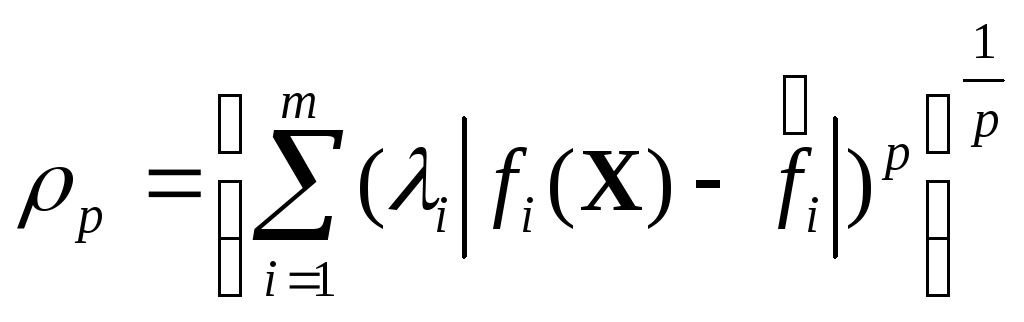где рможет быть любым целым положительным числом и. Так как возведение в степеньявляется монотонным преобразованием, то на положение экстремума оно не влияет. Таким образом, многокритериальная задача сводится к минимизации функции

(10.20)

где - веса отклонений, задаваемые ЛПР(=1,>0). На практике чаще используют значениер=2. В соответствии с теоремой 5 минимизация такой функции приводит к эффективному решению.

Как и ранее, целесообразно использовать отклонения в относительных единицах, для чего выражение в квадратных скобках в (10.20) можно разделить на .

Пример 10.3. Найдем решение для модели из примера 10.1 при одинаковых ир=2. Так как =12,=24 и =10, обобщенный критерий запишется в соответствии с (10.20) в виде

.

После отбрасывания общего множителя (1/3), свободного члена (820) и простых преобразований приходим к выражению

.

Используя метод квадратичного программирования, получаем: х=2,97,х=1 ,52 (точка M на рис.10.9). В этой точке f₁=-5.87, f₂=16.44,f₃=-1.66.

Метрика с р=дает уже рассмотренный ранее подход: критериальная функция определяется как максимальное отклонение

, (10.21)

которое следует минимизировать по XD

Пример 10.4. Если воспользоваться сверткой (10.21) для модели из примера10.1, то получим решение:х=1,52,х=1,37 (точка N на рис. 10.9), в которомf₁=-1,82, f₂=10,19, f₃=-3,81.

Пример 10.5. Пусть требуется максимизировать два критерия

f₁(X)=-2x₁+x₂,,

f₂(X)= 4x₁- x₂

при условиях

x₁+x₂8,

-x₁+x₂2,

0 x₁6, 0 x₂4.

Т

R

ак как задача содержит две переменные и два критерия, множества D иGпредста­ви­мы на плоскос­ти, что позво­ляет наглядно сравнить резу­ль­таты рассмот­ренных подхо­дов (рис.10.11).

Решения этой задачи, полученные при различных способах свертки, сведены в следующую таблицу.

№	Обобщенный критерий	Решение
		Рис. 10.11	Х1	Х2	Y1	Y2
1		A	0	2	2	-2
2		K	6	0	-12	24
3		[K,E]	6	[0,2]	[-12,-10]	[24,22]
4		L	1	3	1	1
5		P	1,176	3,176	0,824	1,53
6		M			-7,7	18,2
7		N	4,75	3,25	-6,25	15,75
8		R	4,08	3,92	-4,24	12,4

Здесь квадратными скобками обозначены интервалы, соответствующе множеству решений, оптимальных по данному обобщенному критерию. Как видно из таблицы, линейная свертка с равными весовыми коэффициентами (строка 3) дает весьма однобокий результат: значения второго критерия лежат в области максимума, а первого – в области минимума. Максиминная свертка дала равные абсолютные значения критериев, но второй критерий сильнее, чем первый, отличается от своего максимально возможного значения (строка 4). Очевидно, если использовать в этой свертке относительные величины критериев, взяв за базу, например, разность(maxf_i-minf_i ), то можно ожидать более "справедливого" соотношения значений критериев в оптимальном решении. Действительно, максимизация минимальной относительной величины критерия с весовым коэффициентом приводит к увеличениюf₂и уменьшениюf₁ (строка 5). Следующие два решения, представленные в 6 и 7 строках таблицы, минимизируют отклонения от идеальной точкиI. Результат, соответствующий минимуму суммы квадратов отклонений. можно получить геометрически. Так при одинаковых значениях , как в нашем случае, линии равного уровня обобщенного критерия представляют собой окружности с центром в идеальной точке. Точка минимума есть точка касания линии равного уровня и границы области достижимостиG, а так как у нас линии - окружности, то это будет основание перпендикуляра, опущенного из идеальной точки на ближайшую границуG(точка M). Использование минимаксного отклонения приводит к выравниванию отклонений критериев: если в точке M отклонения составляют 9,7 и 5,8, то в точке N - 8,25 для обоих критериев. Решение по максимальному относительному отклонению представлено в строке 8 таблицы и точкойR на рис 10.11.

Таким образом, все способы свертки дают решения, принадлежащие паретовскому множеству, которое лежит на ломаной КЕСВА (рис.10.11).