4.2.5. Задача планирования работы оборудования

Фирма получила заказ на производство своей продукции. Оборудование, которым располагает фирма, является взаимозаменяемым. Известны нормы времени работы оборудования по каждому виду продукции. Требуется найти наилучший вариант выполнения заказа,

Очевидно, что за критерий следует принять время выполнения заказа, и чем оно меньше, тем лучше. Введем переменные x_ij – количество продукцииi-го вида, произведенного наj-м оборудовании.

Ограничившись тремя видами продукции и двумя видами оборудования, представим исходные данные и все переменные в таблице (табл. 4.5).

Таблица 4.5

Продукция	Оборудование		Заказ
	1	2
1	4 х11	10 х12	70
2	7 х21	5 х22	90
3	3 х31	6 х32	45

Цифры в правом верхнем углу клеток второго и третьего столбцов показывают норму времени на производство единицы продукции.

Составим модель задачи. Требование обязательного выполнения заказа порождает 3 ограничения-равенства:

x₁₁ + x₁₂=70,

x₂₁ + x₂₂=90, (*)

x₃₁ + x₃₂=45.

Для записи критерия подсчитаем время работы первого оборудования

4х₁₁+7х₂₁+3х₃₁

и время работы второго оборудования

10х₁₂+5х₂₂+6х₃₂.

Время выполнения заказа T будет определяться максимальным из них. Таким образом, целевая функция задачи принимает вид

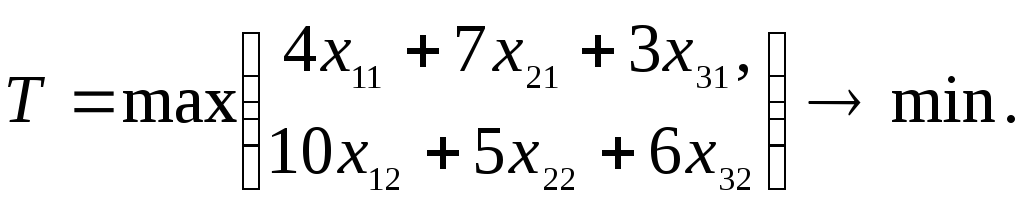
Очевидно, что она и, следовательно, модель в целом не являются линейными. Однако такая модель легко преобразуется к линейной. Действительно, величина T как максимальная из двух времен должна быть не меньше каждого из них, то есть

4х₁₁+7х₂₁+3х₃₁ T,

10х₁₂+5х₂₂+6х₃₂ T. (**)

Рассматривая T как переменную, запишем критерий следующим образом:

L= T →min.

Этот линейный критерий совместно с условиями (**) эквивалентен исходной нелинейной целевой функции.

В итоге мы пришли к линейной модели, которая включает критерий L, ограничения (*), (**) и условия неотрицательности

x_ij0,  i, j.

4.2.6. Игра двух лиц с нулевой суммой как задача линейного программирования

Рассмотрим платежную матрицу игры двух лиц, не имеющую седловых точек,

	B1	B2	…	Bn
A1	U11	U12	…	U1n
A2	U21	U22	…	U2n
…	…	…	…	…
Am	Um1	Um2	…	Umn

где платежи U_ij имеют смысл выигрышей игрока A.

Как известно, такая игра имеет решение в области смешанных стратегий. Пусть X=(x₁,x₂,…,x_m) – распределение вероятностей на стратегиях игрока A. Тогда согласно принципу гарантированного результата этот игрок будет выбирать такое поведение (распределение X ^*), которое максимизирует наименьший ожидаемый выигрыш

.

Обозначим через  минимальный ожидаемый выигрыш

.

Отсюда очевидно, что  не больше каждого ожидаемого выигрыша, и так как цель – максимальный выигрыш, то приходим к следующей эквивалентной задаче

L=→max

при ограничениях

,

х_i0.

Это обычная линейная задача, оптимальное значение критерия которой L^*=^* есть цена игры. Ее решение определяет оптимальное поведение игрока А.

Для игрока B линейная модель строится аналогично, но тот же критерий минимизируется, так как  уже имеет смысл максимального проигрыша, а ограничения на вероятности y_j соответствуют строкам платежной матрицы и записываются как неравенства “меньше или равно”.