4.2.7. Резюме

Рассмотренные модели задач объединяет одно свойство: все функции, входящие в модель (целевая и ограничения), являются линейными относительно искомых переменных. Нетрудно видеть, что задача описывается линейной моделью, если справедливы 3 свойства:

• аддитивности (сложение составляющих затрат, прибыли, времени и т.д.);

• пропорциональности (прибыль, расход пропорциональны количеству продкукции, услуг);

• непрерывности переменных.

Несмотря на сходство в главном, приведенные модели отличаются по виду экстремума (max или min) и/или по виду ограничений (равенства, неравенства, знаки неравенств). Возможны также задачи, в которых часть переменных не имеет ограничений по знаку (например, температура в градусах Цельсия, величина дебаланса, отклонение от заданного значения и т.п.). Чтобы абстрагироваться от этих несущественных отличий при использовании методов решения линейных задач, модели приводят к некоторому единому виду. Основными являются две формы представления задач ЛП, которые рассматриваются ниже.

4.3. Формы записи задач линейного программирования и способы приведения к ним

4.3.1. Каноническая форма задач лп

Задача ЛП представлена в канонической форме, если в ее модели все функциональные условия имеют вид равенств и все переменные ограничены по знаку. Направление цели не имеет существенного значения, но для однозначности канонического представления будем иметь в виду максимизацию критерия. Тогда модель задачи ЛП в канонической форме записывается следующим образом

Если использовать векторно-матричные представления, то получим

L = max

или

где верхний индекс T означает транспонирование;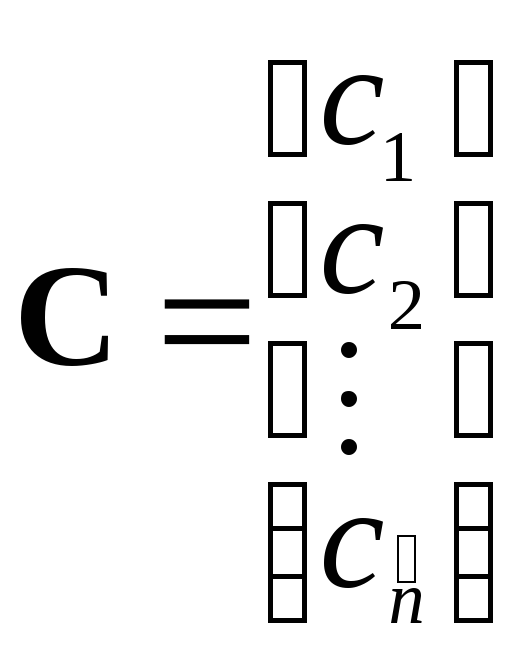 – вектор коэффициентов целевой функции; – векторы условий, j=– вектор ограничений или вектор свободных членов, иногда используют сокращение ССЧ (столбец свободных членов);

–матрица условий; – вектор переменных;– число переменных в канонической форме, оно не меньше числа переменных в исходной модели

Любую задачу ЛП можно привести к каноническому виду. Возможны 3 случая несоответствия исходной модели каноническому представлению. В каждом из них простое преобразование позволяет получить требуемый вид.

1.Если в исходной постановке критерий минимизируется, то изменив знак критерия на обратный, приходим к задаче максимизации, т.е. еслито

2.В исходной модели есть неравенства. При этом способ преобразования зависит от знака неравенства. В случае неравенства очевидно, что разность правой и левой части будет неотрицательной и неизвестной величиной, которую можно принять за новую переменную:

Отсюда получаем следующее равенство:

Таким образом, чтобы привести рассмотренное неравенство к равенству, нужно к левой части неравенства прибавить новую переменную.

Аналогично поступаем с неравенством Но теперь новая переменная обозначает разность левой и правой части

и равенство записывается в виде

то есть чтобы неравенство типа “больше или равно” привести к равенству, следует из левой части вычесть новую переменную. В отличие от исходных переменных такие вновь вводимые переменные будем называть дополнительными. Нетрудно видеть, что они по определению являются неотрицательными, что соответствует каноническому представлению модели.

3.Некоторые переменные исходной модели не имеют ограничения на знак. Исключение таких переменных производится следующим способом.

Пусть – переменная, которая может иметь любой знак. Введем две неотрицательные переменные иво всей модели заменяем их разностью:

Таким образом, последние два случая преобразования к каноническому виду приводят к увеличению числа переменных, и поэтому всегда

Пример 4.1. Исходная модель:

Каноническая модель: