Week 4: Systems of Particles, Momentum and Collisions

189

4.1.2: Coarse Graining: Continuous Mass Distributions

Suppose we wish to find the center of mass of a small cube of some uniform material – such as gold, why not? We know that really gold is made up of gold atoms, and that gold atoms are make up of (elementary) electrons, quarks, and various massless field particles that bind the massive particles together. In a cube of gold with a mass of 197 grams, there are roughly 6 × 1023 atoms, each with 79 electrons and 591 quarks for a total of 670 elementary particles per atom. This is then about 4 × 1026 elementary particles in a cube just over 2 cm per side.

If we tried to actually use the sum form of the definition of center of mass to evaluate it’s location, and ran the computation on a computer capable of performing one trillion floating point operations per second, it would take several hundred trillion seconds (say ten million years) and – unless we knew the exacly location of every quark – would still be approximate, no better than a guess.

We do far better by averaging. Suppose we take a small chunk of the cube of gold – one with cube edges 1 millimeter long, for example. This still has an enormous number of elementary particles in it

– so many that if we shift the boundaries of the chunk a tiny bit many particles – many whole atoms are moved in or out of the chunk. Clearly we are justified in talking about the ”average number of atoms” or ”average amount of mass of gold” in a tiny cube like this.

A millimeter is still absurdly large on an atomic scale. We could make the cube 1 micron (1×10−6 meter, a thousandth of a millimeter) and because atoms have a “generic” size around one Angstrom

– 1 × 10−10 meters – we would expect it to contain around (10−6/10−10)3 = 1012 atoms. Roughly a trillion atoms in a cube too small to see with the naked eye (and each atom still has almost 700 elementary particles, recall). We could go down at least 1-2 more orders of magnitude in size and still have millions of particles in our chunk!

A chunk 10 nanometers to the side is fairly accurately located in space on a scale of meters. It has enough elementary particles in it that we can meaningfully speak of its ”average mass” and use this to define the mass density at the point of location of the chunk – the mass per unit volume at that point in space – with at least 5 or 6 significant figures (one part in a million accuracy). In most real-number computations we might undertake in the kind of physics learned in this class, we wouldn’t pay attention to more than 3 or 4 significant figures, so this is plenty.

The point is that this chunk is now small enough to be considered di erentially small for the purposes of doing calculus. This is called coarse graining – treating chunks big on an atomic or molecular scale but small on a macroscopic scale. To complete the argument, in physics we would generally consider a small chunk of matter in a solid or fluid that we wish to treat as a smooth distribution of mass, and write at first:

m = ρ V

(355)

while reciting the following magical formula to ourselves:

The mass of the chunk is the mass per unit volume ρ times the volume of the chunk.

We would then think to ourselves: “Gee, ρ is almost a uniform function of location for chunks that are small enough to be considered a di erential as far as doing sums using integrals are concerned. I’ll just coarse grain this and use integration to evaluation all sums.” Thus:

dm = ρ dV

(356)

We do this all of the time, in this course. This semester we do it repeatedly for mass distributions, and sometimes (e.g. when treating planets) will coarse grain on a much larger scale to form the “average” density on a planetary scale. On a planetary scale, barring chunks of neutronium or the occasional black hole, a cubic kilometer “chunk” is still “small” enough to be considered di erentially

190	Week 4: Systems of Particles, Momentum and Collisions

small – we usually won’t need to integrate over every single distinct pebble or clod of dirt on a much smaller scale. Next semester we will do it repeatedly for electrical charge, as after all all of those gold atoms are made up of charged particles so there are just as many charges to consider as there are elementary particles. Our models for electrostatic fields of continuous charge and electrical currents in wires will all rely on this sort of coarse graining.

Before we move on, we should say a word or two about two other common distributions of mass. If we want to find e.g. the center of mass of a flat piece of paper cut out into (say) the shape of a triangle, we could treat it as a “volume” of paper and integrate over its thickness. However, it is probably a pretty good bet from symmetry that unless the paper is very inhomogeneous across its thickness, the center of mass in the flat plane is in the middle of the “slab” of paper, and the paper is already so thin that we don’t pay much attention to its thickness as a general rule. In this case we basically integrate out the thickness in our minds (by multiplying ρ by the paper thickness t) and get:

m = ρ V = ρt A = σ A	(357)
where σ = ρt is the (average) mass per unit area of a chunk of paper with area	A. We say our
(slightly modified) magic ritual and poof! We have:
dm = σ dA	(358)

for two dimensional areal distributions of mass.

Similarly, we often will want to find the center of mass of things like wires bent into curves, things that are long and thin. By now I shouldn’t have to explain the following reasoning:

m = ρ V = ρA x = λ x

(359)

where A is the (small!) cross section of the solid wire and λ = ρA is the mass per unit length of the chunk of wire, magic spell, cloud of smoke, and when the smoke clears we are left with:

dm = λ dx

(360)

In all of these cases, note well, ρ, σ, λ can be functions of the coordinates! They are not necessarily constant, they simply describe the (average) mass per unit volume at the point in our object or system in question, subject to the coarse-graining limits. Those limits are pretty sensible ones – if we are trying to solve problems on a length scale of angstroms, we cannot use these averages because the laws of large numbers won’t apply. Or rather, we can and do still use these kinds of averages in quantum theory (because even on the scale of a single atom doing all of the discrete computations proves to be a problem) but then we do so knowing up front that they are approximations and that our answer will be “wrong”.

In order to use the idea of center of mass (CM) in a problem, we need to be able to evaluate it. For a system of discrete particles, the sum definition is all that there is – you brute-force your way through the sum (decomposing vectors into suitable coordinates and adding them up).

For a solid object that is symmetric, the CM is “in the middle”. But where’s that? To precisely find out, we have to be able to use the integral definition of the CM:

Z

~

M Xcm = ~xdm (361)

R

(with M = dm, and dm = ρdV or dm = σdA or dm = λdl as discussed above).

Let’s try a few examples:

~ L2

M Xcm = λ 2

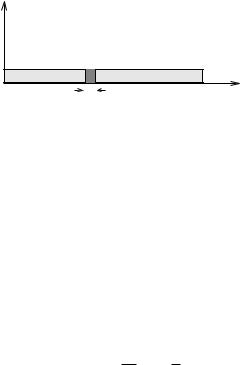
Week 4: Systems of Particles, Momentum and Collisions

191

	M
	dm = λ dx=___ dx
	L
0	dx	L

Figure 48:

Example 4.1.2: Center of Mass of a Continuous Rod

Let us evaluate the center of mass it is in the middle:

of a continuous rod of length L and total mass M , to make sure

ZZ L

~	λxdx	(362)
M Xcm = ~xdm =
	0

where	dm = Z L λdx = λL
M = Z
	0
(which defines λ, if you like) so that

= M L2

and	L
~
Xcm =	2	.
Gee, that was easy. Let’s try a hard one.

(363)

(364)

(365)

192		Week 4: Systems of Particles, Momentum and Collisions
		dA =r dr dθ	θ0
				dm = σ dA
			r dθ
		r
	0	dr	R
		Figure 49:

Example 4.1.3: Center of mass of a circular wedge

Let’s find the center of mass of a circular wedge (a shape like a piece of pie, but very flat). It is two dimensional, so we have to do it one coordinate at a time. We start from the same place:

M Xcm = Z

xdm = Z0R Z0

θ0

σxdA = Z0R Z0

θ0

σr2 cos θdrdθ

(366)

where

dm = Z0

Z0

σdA = Z0

Z0

σrdrdθ = σ R2θ0

(367)

M = Z

R

θ0

R

θ0

2

(which defines σ, if you like) so that

M Xcm = σ R3 sin θ0

3

from which we find (with a bit more work than last time but not much) that:

2R3 sin θ0

Xcm = 3R2θ .

Amazingly enough, this has units of R (length), so it might just be right. on your own!

(368)

(369)

To check it, do Ycm

Week 4: Systems of Particles, Momentum and Collisions

193

Example 4.1.4: Breakup of Projectile in Midflight

m = m 1+ m 2

v

0

θ	m1	m2

x1

R

x 2

Figure 50: A projectile breaks up in midflight. The center of mass follows the original trajectory of the particle, allowing us to predict where one part lands if we know where the other one lands, as long as the explosion exerts no vertical component of force on the two particles.

Suppose that a projectile breaks up horizontally into two pieces of mass m1 and m2 in midflight. Given θ, v0, and x1, predict x2.

The idea is: The trajectory of the center of mass obeys Newton’s Laws for the entire projectile and lands in the same place that it would have, because no external forces other than gravity act. The projectile breaks up horizontally, which means that both pieces will land at the same time, with the center of mass in between them. We thus need to find the point where the center of mass would have landed, and solve the equation for the center of mass in terms of the two places the projectile fragments land for one, given the other. Thus:

	Find R. As usual:							1
	y = (v0 sin θ)t −									gt2		(370)
								2
	1
	tR(v0 sin θ −					gtR) = 0						(371)
				2
		tR =	2v0 sin θ)									(372)
				g
					2v2 sin θ cos θ
	R = (v0 cos θ)tR =						0				.	(373)
										g
	R is the position of the center of mass. We write the equation making it so:
	m1x1 + m2x2 = (m1 + m2)R											(374)
	and solve for the unknown x2.
	x2 =	(m1 + m2)R − m1x1										(375)
			m2

From this example, we see that it is sometimes easiest to solve a problem by separating the motion of the center of mass of a system from the motion in a reference frame that “rides along” with the center of mass. The price we may have to pay for this convenience is the appearance of pseudoforces in this frame if it happens to be accelerating, but in many cases it will not be accelerating, or the acceleration will be so small that the pseudoforces can be neglected compared to the much larger forces of interest acting within the frame. We call this (at least approximately) inertial reference frame the Center of Mass Frame and will discuss and define it in a few more pages.

First, however, we need to define an extremely useful concept in physics, that of momentum, and discuss the closely related concept of impulse and the impulse approximation that permits us to treat the center of mass frame as being approximately inertial in many problems even when it is accelerating.