18. Математическое ожидание и дисперсия непрерывной случайной величины и их свойства (без доказательства).

Математическое ожидание непрерывной случайной величины называется число

М(Х) = ∫хf(x)dx.

Две случайные величины (произвольные, непрерывные или дискретные) Х и Yназываются независимыми, если для всех х,y€R

P[(X<x) ∩ (Y<y)] = P (X<x) P(Y<y),

Т.е. если для всех х,y€Rсобытия (Х<x) и (Y<y) независимы.

Свойства:

4. М(С) = С, С =const

5. М(СХ) = С*М(Х), С = const

6. М(Х+Y) = М(Х) + М(Y), Х иY– дискретные случайные величины.

Дисперсия случайной величины:

D(X)=∫(x-M(x)²f(x)dx, D(x)=∫x²f(x)dx-(M(x))²

Свойства:

4. D(C) = 0

5. D(CX) = C²D(X)

6. D(X+Y) =D(X) +D(Y),XиY– независимые дискретные случайные величины.

19. Начальные и центральные моменты.

Начальным моментом порядка kслучайной величины Х называют математическое ожидание величины Х^k:v_k=M(X^k).

В частности, начальный момент первого порядка равен математическому ожиданию: v₁=M(x).

Центральным моментом порядка kслучайной величины Х называют математическое ожидание величины (Х-М(Х))^k:μ_{k =} М(Х-М(Х))=0;

В частности, центральный момент первого порядка равен 0:

μ₁ = М(Х-М(Х))=0;

центральный момент второго порядка равен дисперсии:

μ₂= М(Х – М(Х))²=D(X).

Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные:

μ_{2 =} v₂-v₁²,

μ₃ = v₃ – 3v₁v₂ +2v₁³,

μ₄=v₄-4v₁v₃+6v₁²v₂-3v₁⁴.

20. Равномерный закон распределения: плотность и функция распределения, основные числовые характеристики.

Например минутная стрелка остановившихся механических часов будет показывать какое-то значение; заранее, до поломки, неизвестно, какое именно, но точно известно, что оно будет в пределах от 0 до 60. Погрешность округления также относится к подобным величинам. О таких величинах говорят, что они распределены по равномерному закону на некотором отрезке [a,b].

Более строго, случайная величина Х с функцией распределения

Называется распределенной по равномерному законуна отрезке [a,b].Плотность распределения получается путем дифференцирования:

Математическое ожиданиенепрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством:

М(Х) = ∫xf(x) dx

Где f(x) – плотность распределения случайной величины Х.

МодойМ₀(Х) непрерывной случайной величины Х называют ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.

МедианойМ_е(Х) непрерывной случайной величины Х называют то ее значение, которое определяется равенством

Р[X<M_e(X)]=p[X>M_e(X)].

Дисперсиянепрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

D(X) = ∫[x-M(X)]²f(x)dxилиD(X) = ∫x²f(x)dx– [M(X)]²

Среднее квадратичное отклонениенепрерывной случайной величины определяется

σ(Х) = √D(X)

21. Показательный закон распределения: плотность и функция распределения, основные числовые характеристики.

Показательным называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

0 при x<0,

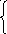f(x) =

λe^-λxприx>=0

где λ – постоянная положительная величина.

Функция распределения показательного закона

0 приx<0

F(x) = 1-е^-λх приx>=0

Вероятность попадания в интервал (a,b) непрерывной случайной величины Х, распределенной по показательному закону,

P(a<X<b) = e^-λa-e^-λb

Математическое ожидание- М(Х) = 1/μ.Дисперсия-D(X) = 1/μ²

22. Поток событий. Простейший поток. Распределение промежутка времени между последовательными событиями простейшего потока. Свойство марковости показательного закона.

24. Нормальный закон распределения: функция плотности и функция распределения, основные числовые характеристики.

Нормальнымназывают распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид

F(x) = (1/σ√2π) * e^-(x-a)2/^/(2σ2)

Где a– математическое ожидание, σ – среднее квадратичное отклонение Х.

Вероятность того, что Х примет значение, принадлежащее интервалу (α, β),

P(α<X< β) = Ф(β- а/ σ) – Ф(α- а/ σ),

Где Ф(х) = 1/√2π∫е^-х2/2dx– функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше положительно числа δ,

Р(!X-a! <δ) = 2Ф(δ/σ).

25. Функция Лапласа и ее свойства. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило «трех сигм».

26. Неравенство Чебышева. Понятие о законе больших чисел. Теорема Чебышева ( без док-ва). Теорема Бернулли (без док-ва).

Неравенство Чебышева:Если случайная величина Х имеет конечное математическое ожидание М(Х) и дисперсиюD(Х) , то для любого ε>0 справедливо равенство

P{|X–M(X) | <=ε} > 1-D(X)/ε²

Под закономбольших чисел понимается обобщенное название группы теорем, утверждающих, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.

Теорема Чебышева: Если дисперсии независимых случайных величин Х₁,Х₂,…,Хnограничены сверху числом В, то для произвольного, сколь угодно малого ε>0 справедливы неравенство

Р{|∑X_i/n- ∑M(X_i)/n| <=ε}> 1 –B/nε²

и предельное равенство limP{|∑X_i/n- ∑M(X_i)/n| <=ε} = 1

Теорема Бернулли: Если вероятность успеха в каждомnнезависимых испытаний постоянна и равнаp, то для произвольного, сколь угодно малого ε>0 справедливо равенство

limP{|m/n-p|<=ε}=1,

где m– число успехов в серии изnиспытаний.