нечітка_логіка-лаб

			(x c	)2
	exp		1
			2		, x c1 ;
			2a1
если c1 c2 ,	то μ(x) 1,				с1 x c2 ;		(9)
			(x c	)2
			1			2 .
	exp		2a12		, x c

			(x c	)2
	exp		1			2	;
			2		, x c
			2a1
если c1 c2 ,	то μ(x) 1,				с2 x c1 ;			(10)
			(x c	)2
			1				;
	exp		2a12		, x c1

Якщо	c1	c2 , то	параметри функції	приналежності геометрично
інтерпретуються наступним чином:
c1 (c 2 ) - мінімальне (максимальне) значення ядра нечіткої множини;
a1 (a 2 )	-	коефіцієнт	концентрації лівої	(правої) частини функції

приналежності.

Коли c1 c2 , нечітка множина є субнормальною.

Функція gauss2mf застосовується для завдання гладких асиметричних функцій приналежності і має два вхідних аргументи:

x - вектор, для координат якого необхідно розрахувати ступеня належності; params - вектор параметрів функції належності. Порядок завдання

параметрів - [a1 ,c1 ,a 2 ,c2 ].

Функція gauss2mf повертає вихідний аргумент y , що містить ступеня приналежності координат вектора x .

Рис. 8 - Проста і двостороння функції приналежності Гауса

Наступною функцією, яка дозволяє представляти нечіткі множини, є ФП «узагальнений дзвін» і позначається gbellmf. Її відмінність від розглянутих раніше ФП полягає в додаванні третього параметра, що дозволяє здійснювати плавний перехід між нечіткими множинами.

Аналітичний запис:

f(x, a, b,c)		1
	1		x c		2b
			a

де a - коефіцієнт концентрації функції належності; b - Коефіцієнт крутизни функції належності;

c - Координата максимуму функції належності.

Опис функції в MATLAB:

y gbellmf(x, [a b c])

Вид функції зображений на рис. 9.

Рис. 9 - Функція приналежності «узагальнений дзвін»

, (11)

(12)

Функції приналежності на основі функції розподілу Гауса і ФП «узагальнений дзвін» відрізняються гладкістю і простотою запису і є найбільш використовуваними при описі нечітких множин. Недоліком даних функцій є те, що вони не дозволяють формувати асиметричні ФП. Для цих цілей передбачений набір сігмоідних функцій, які можуть бути відкриті або ліворуч, або праворуч в залежності від типу функції. Основна сігмоідна ФП позначається sigmf, а

додаткові - dsigmf і psigmf.

Аналітичний вид основної сігмоідної функції:

f(x, a,c)	1	(13)

1 e-a(x-c)

Параметри сігмоідної функції геометрично інтерпретуються наступним чином:

a - коефіцієнт крутизни функції належності;

c - координата перегину функції приналежності.

Залежно від знака параметра а розглянута ФП буде відкрита справа або зліва (рис. 10), що дозволить застосовувати її при описі таких нечітких понять, як «дуже високий», «вкрай негативно» та ін.

Завдання функції в MATLAB:

y sigmf(x, [a c])	(14)
Опис додаткових сігмоїдних функцій:
y dsigmf(x, [a1 , c1 , a 2 , c2 ])	(15)

Функція приналежності у вигляді різниці між двома сігмоїдними функціями:

μ(x)	1		1
	1 e-a1(x-c1)		1 e-a2 (x-c2 )

Добуток двохсігмоїдної функції приналежності

y psigmf(x, [a1 , c1 , a 2 , c2 ])

(16)

(17)

Функція psigmf являє собою добуток двох сігмоїдних функцій приналежності:

μ(x)	1		1
	1 e-a1(x-c1)		1 e-a2 (x-c2 )

Обидві ФП застосовуються для завдання гладких приналежності.

(18)

асиметричних функцій

Рис. 10 - Сігмоідні ФП: основна одностороння, додаткова двостороння і додаткова несиметрична

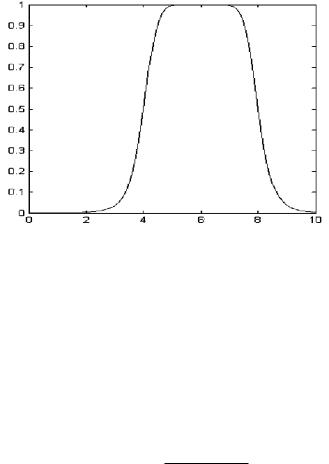
Інструментарій нечіткої логіки (Fuzzy Logic Toolbox) у складі MATLAB надає можливість формування ФП на основі поліноміальних кривих. Відповідні функції називаються Z- функціями (zmf), PI-функції (pimf) і S-функції (smf). Функція zmf являє собою асиметричну поліноміальну криву, відкриту зліва (рис. 11, а), функція smf - дзеркальне відображення функції zmf (рис. 11, б). Відповідно функція pimf дорівнює нулю в правому і лівому межах і приймає значення, рівне одиниці, в середині деякого відрізка (рис. 11, в). Опис функцій:

y zmf(x, [a b])

(19)

Параметри a і b визначають екстремальні значення кривої (рис. 11, а).

y pimf(x, [a	b	c d])	(20)
Параметри a і d визначають перехід		функції в нульове	значення, а
параметри b і c в одиничне (рис. 11, в).
y smf(x, [a	b])		(21)

Параметри a і b визначають екстремальні значення кривої (рис.

11, б).

Рис. 11 - Поліноміальні функції приналежності: а - Z-функція; б - S-функція;

в- Pi-функція

2.Порядок виконання роботи

1.Ознайомитися з основними видами функцій належності нечітких множин. Ознайомитися зі стандартними видами функцій приналежності, що входять в пакет Fuzzy Logic Toolbox.

2.Вивчити способи формування функцій приналежності (з параметрами відповідно до варіанту, таблиця 1).

3.Ознайомитися з можливостями системи MATLAB для роботи з нечіткими множинами.

4.Підібрати необхідні параметри функцій приналежності і застосувати операції об'єднання (за допомогою операції max, алгебраїчне, граничне, драстіческое), перетину (за допомогою операції min, алгебраїчне, граничне, драстіческое) та доповнення до заданих нечітким множинам. Результати представити графічно.

5.Оформити звіт про виконану роботу.

6.Відповісти на контрольні питання.

3. Вихідні дані

	Таблиця 1
№ Варіанта	ФП
1	Трикутна
2	Трапецієвидна
3	Гауса
4	Двостороння Гауса
5	Узагальнений дзвін
6	Основна одностороння сігмоідна
7	Додаткова двостороння сігмоідна
8	Додаткова несиметрична сігмоідна
9	Поліноміальна Z-функція
10	Поліноміальна S-функція

4. Контрольні питання

1.Які види функцій приналежності нечітких множин ви знаєте?

2.Наведіть опис трикутної функції приналежності в аналітичному вигляді і

впрограмному комплексі MATLAB.

3.Наведіть опис трапецієподібної функції належності в аналітичному вигляді і в програмному комплексі MATLAB.

4.Наведіть опис простий і двосторонньої функцій приналежності Гаусса в аналітичному вигляді і в програмному комплексі MATLAB.

5.Наведіть опис сігмоідную функцій приналежності в аналітичному вигляді і в програмному комплексі MATLAB.

ЛАБОРАТОРНА РОБОТА №3 ФОРМУВАННЯ БАЗИ ПРАВИЛ НЕЧІТКОЇ СИСТЕМИ МОДЕЛЮВАННЯ

НЕЛІНІЙНОЇ СИСТЕМИ

Мета роботи: знайомство з методологією нечіткого моделювання шляхом опису заданої нелінійної функції безліччю правил виду ЯКЩО-ТО.

1. Знайомство з методологією нечіткого моделювання

Опис предметної області може бути проведено за допомогою лінгвістичних змінних і правил природної мови, що містять ка¬чественную оцінку ситуації.

Основою для опису ситуації є не¬четкое вислів наступного виду: x i є X i чи x i - X i , де x i - деяка величина, X i - елемент терм-множини лінгвістичної змінної з

досліджуваної предметної області.
Нечітка система виконує відображення з вхідного простору			A m	в
вихідний	простір В r . Така система є системою типу	«багато_входів-
багато_виходів» (MIMO-multiple_input-multiple_output). Якщо		система має		m
входів і r	виходів, та вхідний і вихідний простори є багатовимірними,		то вхідний
простір визначається як A A1 ... A m , а вихідна простір – як		B B1 ... Br ,		де
A i , B j .	Визначимо a [a 1a 2 ...a m ]T і b [b1 b 2 ...b r ]T як вхідний і вихідний вектори,
відповідно.

Відображення вхід / вихід може бути представлено як безліч не¬четкіх правил типу «ЯКЩО-ТО». Кожне правило складається з двох частин: ус¬ловной та заключної. Антецедент або умовна частина (ЯКЩО-частина) со¬держіт твердження щодо значень вхідних змінних, в консеквент або заключній частині (ТО-частини) вказуються значення, що беруть вихідні змінні. Таким чином, нечітка система типу «багато_входів-багато_виходів» може бути задана нечіткими правилами такого вигляду:

Правило1: ЯКЩО a1 A11 И			a 2 A21 ... a m	Am1
ТО b1	В11	И b2	В21 И ...И br	Вr1;
Правило 2 : ЯКЩО	a1 A12 И		a 2 A22 ... a m	Am2
ТО b1 В12		И b2 В22 И ...И br		Вr2 ;
.................................................................................................
Правило n : ЯКЩО a1 A1n И a 2 A2n ... a m Amn
ТО b1 В1n		И b2 В2n И ...И br		Вrn ;
де a1a 2 ...a m - вхідні змінні, b1b 2 ...b r -		вихідні змінні, A it		і B j s - нечіткі області

визначення вхідних і вихідних змінних, які визначені на універсальних множинах X1 , X2 ,..., Xm , Y1 , Y2 ,..., Yr , відповідно. Кожна нечітка область A it пов'язана з

функцією приналежності μ Ait (a i ) .

Вхід A нечіткої системи активізує кожне з правил, збережених в нечіткій асоціативної пам'яті. Чим більше вхід A відповідає антеценденту i -го правила, тим більше вихід відповідає консеквенту цього правила.

Вельми популярними в практичному застосуванні в даний час є нечіткі системи типу «багато_входів - один_вихід». Система такого типу виконує відображення з вхідного простору A m в вихідний простір В r . Відомо два основних типи нечітких систем «багато_входів - один_вихід». Системи типу Мамдані мають правила:

Правило i : ЕСЛИ a i A1i И a 2 A 2i ... a m A m1 ТО bi Вi ;

Інший тип - системи типу Сугено з правилами такого вигляду:

Правило i : ЕСЛИ a i A1i

И a 2 A 2i

... a m A m1

ТО bi fi (a 1 ,..., a m );

μ B (y)

де fi - функція, визначена на змінних a1,..., am .

Для опису відображення вхідного вектора в значення використовуються методи нечіткої логіки, наприклад, апроксимація Мамдані або метод, заснований на формальному логічному доказі. У процесі виводу беруть участь операції кон'юнкції і диз'юнкції. Завдання цих операцій на основі триангулярних норм дозволяє більш гнучко налаштовувати нечітку систему на досліджувану предметну область.

У загальному випадку процес створення нечітких систем складається з наступних кроків:

1.Визначення вхідних і вихідних змінних системи;

2.Завдання функцій приналежності кожної змінної;

3.Визначення нечітких правил;

4.Налаштування параметрів функцій належності та нечітких правил.

При розробці бази правил необхідно керуватися наступними принципами: 1) У базі правил існує правило для всяких поєднань A1i , A 2i ,..., A mi , Bi ;

2) Немає двох і більше правил з однаковим антецедентом і різним консеквентом.

Для здійснення виводу в такій системі можна скористатися композиційним правилом. Однак попередньо потрібно виконати опе¬раціі кон'юнкції і далі операцію об'єднання (агрегації) n правил.

Нехай на вхід системи надходять чіткі значення. Потрібно

визначити чіткий вихід . Для цього необхідно виконати наступні операції:

a. Фазифікації - для кожного правила обчислюється значення μ A1t (x1 ) і

μA2t (x 2 ) ;

b.Кон'юнкції - об'єднання посилок в антецеденті кожного правила, використовуючи t-нормальну функцію, отримаємо T(μA1(x1 ), μA2 (x 2 )) ;

c.Імплікації - I(T(μA1i (x1 ), μA2i (x 2 )), μBi (y)) ;

d.Агрегації - отримання нечіткого вихідного значення з множини

об'єднаних правил, тобто визначення підсумкової функції приналежності μ B (y) .

e. Дефаззіфікації - перетворення підсумкової функції приналежності в чітке значення y .

Структура нечіткої системи моделювання представлена на рис.1.1.

Рис. 12 - Структура нечіткої системи моделювання

2. Опис заданої нелінійної функції безліччю правил виду ЯКЩО-ТО

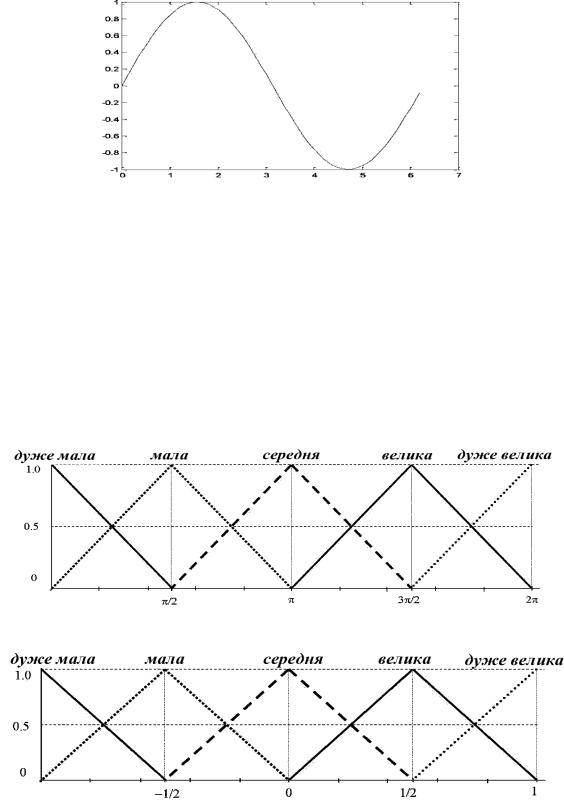
Нехай дана функція F(x) sin(x) і наступні області зміни

(рис. 13).

Рис. 13 - Приклад нелінійної функції

0 x 2 pi, 1 y 1

Лінгвістичні змінні, що описують x і F, визначені на наступному безлічі термів: {дуже мала, мала, середня, велика, дуже велика}. Функції приналежності для зазначених термів наведені на малюнках 14 і 15 Тоді нечітка система моделювання зазначеної нелі¬нейной функції буде заданна наступній базою правил:

ЕСЛИ	x дуже	мала		ТО	F середня,
ЕСЛИ	x мала			ТО	F дуже велика,
ЕСЛИ	x середня			ТО	F середня,
ЕСЛИ	x велика			ТО	F дуже мала,
ЕСЛИ	x дуже	велика		ТО	F середня.

Рис. 14 - Приклад функцій приналежності для змінної

Рис. 15 - Приклад функцій приналежності для змінної F

3. Вихідні дані

Таблиця 2

№	Функція	Область змін
		x	y	z
1	z = x + sin(y - pi/2)	-2<x<2	- pi <y< pi	-1<z<4
2	z = cos(x) + sin(y - pi/2)	- pi <x< pi	- pi <y< pi	-2<z<2
3	z = x * sin(y)	-pi<x<pi	-pi<y<pi	-3<z<3
4	2 2 z = x - y	-4<x<4	-4<y<4	-4<z<4
5	2 * 2 z = x * y	-3<x<3	-3<y<3	0<z<4
6	z = x * y	-3<x<3	-3<y<3	-4<z<4
7	z = (x - y )* y +1	-3<x<3	-3<y<3	-4<z<3
8	z = y * sin(x + y)	-pi/2<x<pi/2	-pi/2<y<pi/2	-0.5<z<1.5
9	z = sin(2*x /pi)* sin(2*y/pi)	-5<x<5	5<y<5	1<z<1
10	z = y * sin(x)	-pi/2<x<pi/2	-pi/2<y<pi/2	1<z<1.5

4. Порядок виконання роботи

1.Використовуючи пакет Matlab або Mathcad, побудувати графік обраної нелінійної функції(згідно з таблицею 2).

2.Обрану нелінійну функцію описати базою правил для лінгвістичних змінних, що описують x і F визначених на множині з п'яти, семи, дев'яти та одинадцяти термів.

3.При виконанні роботи врахувати, що z приймає значення рівне значенню мінімальної або максимальної межі, відповідно. pi = 3,141592653589793238462643

4.Привести уявлення модельованої функції в графічному і формульному

видах.

5.Привести опис чотирьох баз правил для п'яти, семи, дев'яти та одинадцяти термів.

6.Оформити звіт про виконану роботу.

7.Відповісти на контрольні питання.

5. Контрольні питання

1.У чому полягає суть методології нечіткого моделювання?

2.Які правила мають системи типу Мамдані і Сугено?

3.З яких кроків складається процес створення нечітких систем?

4.Які операції необхідно виконати для визначення чіткого виходу функції?

5.Наведіть структуру нечіткої системи моделювання.

ЛАБОРАТОРНА РОБОТА №4

МОДЕЛЮВАННЯ НЕЧІТКОЇ СИСТЕМИ ЗАСОБАМИ FUZZY LOGIC

TOOLBOX СИСТЕМИ MATLAB

Мета роботи:

вивчення основних визначень теорії нечітких множин та теорії нечіткого логічного висновку;

ознайомлення зі складом і можливостями інструментарію нечіткої логіки Fuzzy Logic Toolbox, що входить в пакет програм MATLAB;

набуття практичних навичок роботи в пакеті Fuzzy Logic Toolbox і створення нечіткої моделі управління.

1. Побудова нечіткої апроксимуючої системи

В рамках пакета користувач може виконувати необхідні дії з розробки та використання нечітких моделей в одному з наступних режимів:

в інтерактивному режимі за допомогою графічних засобів редагування і візуалізації всіх компонентів систем нечеткоговивода;

в режимі команд за допомогою введення імен відповідних функцій з необхідними аргументами безпосередньо у вікно команд системи MATLAB.

Для розробки і подальшого застосування систем нечіткого виводу в інтерактивному режимі можуть бути використані наступні графічні засоби, що входять до складу пакету Fuzzy Logic Toolbox:

редактор систем нечіткого виводу Fuzzy Inference System (FIS Editor) або скорочено редактор FIS.

редактор функцій приналежності системи нечіткого виводу (Membership Function Editor) або скорочено редактор функцій приналежності.

редактор правил системи нечіткого виводу (Rule Editor) або скорочено редактор правил.

програма перегляду правил системи нечіткого виводу (Rule Viewer).

програма перегляду поверхні системи нечіткого виводу (Surface Viewer). Крім цих графічних засобів, до складу пакета Fuzzy Logic Toolbox також

входять наступні спеціальні програми.

2. Редактор систем нечіткого виводу

Редактор систем нечіткого виводу FIS (або просто редактор FIS) є основним засобом, який використовується для створення або редагування систем нечіткого виводу в графічному режимі. Редактор FIS може бути відкритий за допомогою введення функції fuzzy або fuzzy ('a') у вікні команд. Ця функція надає користувачеві можливість задавати і редагувати на високому рівні властивості системи нечіткого виводу, такі як число вхідних і вихідних змінних, тип системи нечіткого виводу, використовуваний метод дефазифікації і т. д.