32

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Государственный Университет Управления

Кафедра прикладной математики

Курсовая работа По дисциплине: «Прикладная математика»

Выполнила	Стародубова Екатерина Антоновна
Институт	Управление в химической и металлургической промышленности
Специальность	Менеджмент организации
Специализация	Международный бизнес химических товаров
Вариант	14
Отделение	в/о
Курс	II
Группа	I
Руководитель	Сухоминский В.Л.
Дата сдачи на проверку
Дата защиты
Оценка
Подпись руководителя

Москва 2005

Содержание

1. Задание на курсовую работу 2

2. 1. (1) Линейная производственная задача 4

3. 2. (2) Двойственная задача 12

Задача о "расшивке узких мест производства" 14

3. (3) Транспортная задача линейного программирования 16

4. (4) Динамическое программирование 19

5. (6) Матричная игра как модель конкуренции и сотрудничества 22

6. (14) Матричная модель производственной программы 27

6. (16) Анализ доходности и риска финансовых операций 30

3. Список литературы 32

Задание на курсовОЙ ПрОЕКТ

1. Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов

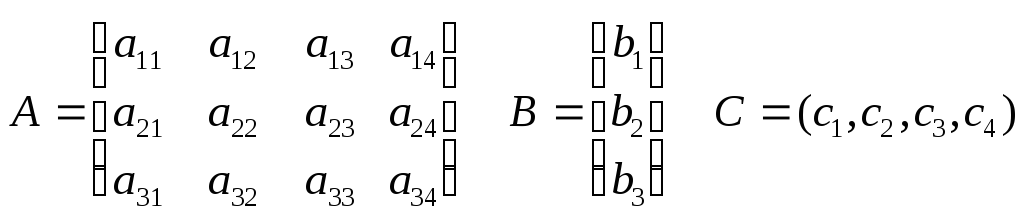
компактно записаны в виде

c₁ c₂ c₃ c₄

а₁₁ а₁₂ а₁₃ а₁₄ b₁

a₂₁ a₂₂ a₂₃ a₂₄ b₂

a₃₁ a₃₂ a₃₃ a₃₄ b₃

Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать узкие места производства.

В последней симплексной таблице указать обращенный базис Q^-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения

H = Q^-1B

Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.

2. Сформулировать задачу, двойственную линейной производственной задаче, как задачу определения расчетных оценок ресурсов, и найти ее решение, пользуясь второй основной теоремой двойственности (о дополняющей нежесткости). Указать оценку единицы каждого ресурса, минимальную суммарную оценку всех ресурсов, оценки технологий.

Применить найденные двойственные оценки ресурсов к решению следующей задачи.

Сформулировать задачу о "расшивке узких мест производства" и составить математическую модель. Определить область устойчивости двойственных оценок, где сохраняется структура программы производства. Решить задачу о расшивке узких мест производства при условии, что дополнительно можно получить от поставщиков не более одной трети первоначально выделенного объема ресурса любого вида (если задача окажется с двумя переменными, то только графически); найти план приобретения дополнительных объемов ресурсов, дополнительную возможную прибыль.

По пунктам 1, 2, 3 составить сводку результатов [10, c. 21].

3. Составить математическую модель транспортной задачи по исходным данным из приложения 2, где вектор объемов производства А(a₁,..., a_m), потребления - В (b₁,..., b_n) и матрица транспортных издержек С=(с_ij), i =; j =кратко записаны в виде

b₁ b₂ . . . b_n

a₁ c₁₁ c₁₂ . . . c_1n

a₂ c₂₁ c₂₂ . . . c_2n

. . . . . . . . . . . . . . . . . . . .

a_m c_m1 c_m2 . . . c_mn

Если полученная модель окажется открытой, то свести ее к замкнутой и найти оптимальное решение транспортной задачи методом потенциалов.

4. Методом динамического программирования решить задачу распределения капитальных вложений между четырьмя предприятиями производственного объединения, располагающего суммой в 700 тыс. руб., по исходным данным, приведенным в приложении 3 (выделяемые суммы кратны 100 тыс.).

6. Рассмотреть матричную игру как модель сотрудничества и конкуренции, взяв исходные данные из приложения 5. Найти графически решение игры. Указать, как проявляется конкуренция между игроками и сотрудничество между ними.

14. Составить матричную модель производственной программы предприятия по исходным данным из приложения 6. По данному вектору выпуска товарной продукции найти вектор производственной программы и полные затраты всех внешних ресурсов.

15. Провести анализ доходности и риска финансовых операций по исходным данным, приведенным в приложении 7.

Линейная производственная задача.

Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов. Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать узкие места производства.

В последней симплексной таблице указать обращенный базис Q^-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения

H = Q^-1B

ИСХОДНЫЕ ДАННЫЕ

27	39	18	20
2	1	6	5	140
0	3	0	4	90
3	2	4	0	198

А - матрица удельных затрат;

В - вектор объёмов ресурсов;

С - вектор удельной прибыли.

а₁₁ а₁₂ а₁₃ а₁₄ в₁

А = а₂₁ а₂₂ а₂₃ а₂₄ ; В= в₂ ; С = (с₁, с₂, с₃, с₄).

а₃₁ а₃₂ а₃₃ а₃₄ в₃

2 1 6 5 140

А = 0 3 0 4 В = 90 С=(27, 39, 18, 20 )

3 2 4 0 198

компактно записаны в виде:

С1	С2	С3	С4			27	39	18	20
a11	a12	a13	a14	B1		2	1	6	5	140
a21	a22	a23	a24	B2		0	3	0	4	90
a31	a32	a33	a34	B3		3	2	4	0	198

Задача– найти производственную программу, максимизирующую прибыль при имеющихся ограниченных ресурсах.

Математическая модель линейной производственной задачи.

1. z(x₁,x₂,x₃,x₄) =c₁x₁+c₂x₂+c₃x₃+c₄x₄max, гдеz- функция прибыли;

z=27x₁+39x₂+18x₃+20х₄max

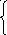(2)a₁₁x₁+a₁₂x₂+a₁₃x₃+a₁₄x₄< в₁- ограниченные ресурсы

а₂₁х₁+а₂₂х₂+а₂₃х₃+а₃₄х₄< в₂;

а₃₁х₁+а₃₂х₂+а₃₃х₃+а₃₄х₄< в₃

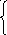
2x₁ + 1x₂+ 6x₃ + 5x₄140̀

3x₂ + 4x₄90

3x₁ + 2x₂+ 4x₃198

(3) x₁0,x₂0,x₃0,x₄0, -условие не отрицательности задачи

Получили задачу на условный экстремум. Для ее решения систему неравенств при помощи неотрицательных неизвестных х₅, х₆, х₇ заменим системой линейных алгебраических уравнений.

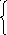
(4) 2x₁ + 1x₂+ 6x₃+ 5x₄+x₅ = 140

3x₂ + 4x₄ +x₆ = 90

3x₁+ 2x₂+ 4x₃+x₇= 198

(5) x₁0,x₂0,x₃0,x₄0,x₅0,x₆0,x₇0.

x₅, x₆,x₇ – имеют смысл остатков соответствующих ресурсов.

Среди всех решений системы уравнений (4), удовлетворяющих условия (5), надо найти то решение, при котором функция (1) примет наибольшее значение.

Воспользуемся тем, что правые части всех уравнений системы (4) неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные х₁, х₂, х₃, х₄, получаем базисное неотрицательное решение.

6. x₁=0,x₂=0,x₃=0,x₄=0,x₅=140,x₆=90,x₇=198.

х₁, х₂, х₃,x₄ - определяют производственную программу.

Из выражения (1) видно, что наиболее выгодно производить продукцию 2-ого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск в этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого запишем для системы уравнений (4) общее решение.

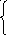
(7) x₅=140 - 2x₁ - 1x₂ - 6x₃ - 5x₄

x₆=90 - 3x₂ - 4x₄

x₇=198 - 3x₁ - 2x₂ - 4x₃

Мы пока сохраняем в общем решении х₁=х₃=х₄=0 и увеличиваем только х₂. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств

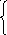
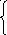
(8) 140 - 1x₂ ≥ 0x₂≤ 140/1

90 - 3x₂ ≥ 0 илиx₂≤ 90/3 т.е. 0≤x₂≤90/3 (выбираем минималь

198 - 2x₂ ≥ 0x₂≤ 198/2 ное значение)

Дадим х₂наибольшее значение х₂ = 90/3, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (8).

x₅=140 – 1*90/3 = 110

x₆=90 – 3*90/3 = 0

x₇=198 – 2*90/3 = 138

Получаем для системы уравнений (4) частное неотрицательное решение

9. x₁=0,x₂=90/3,x₃=0,x₄=0,x₅=110,x₆=0,x₇=138.

Нетрудно убедиться, что это решение является новым базиснымнеотрицательным решением системы линейных алгебраических уравнений (4), для получения которого достаточно было принять в системе (4) неизвестную х₂за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять второе, так как

Min (b_i/a_i2>0) = min (140/1; 90/3; 198/2) = 90/3

А разрешающим элементом будет а₂₂=3. Применив известные формулы исключения, получаем для системы уравнений (4):

Уравнение 4.2 – разрешающее.

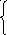
2x₁ + 1x₂+ 6x₃+ 5x₄+x₅ = 140

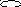(10) 3x₂ + 4x₄ +x₆= 90 - разрешающее уравнение

3x₁+ 2x₂+ 4x₃+x₇= 198

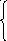2x₁ + 1x₂+ 6x₃+ 5x₄+x₅ = 140

(11) x₂ + 4/3x₄ +x₆/3= 30 (поделили все ур-ние на разреш. коэф. - 3)

3x₁+ 2x₂+ 4x₃+x₇= 198

(12) x₂ + 4/3x₄ +x₆/3= 30 | *1 (т.к. 1 – это коэф. разреш. неизв. в 1-ом ур-нии)

Вычитаем из 1-ого ур-ния найденное.

(13) 2x₁ + 6x₃+11/3x₄+x₅ - x₆/3 = 110 ;

(14) x₂ + 4/3x₄ +x₆/3= 30 | *2 (т.к. 2 – это коэф. разреш. неизв. в 3-ем ур-нии)

(15) 2x₂ + 8/3x₄ +2/3x₆= 60

Вычитаем из 3-его ур-ния найденное.

(16) 3x₁+ 4x₃- 8/3x₄ -2/3x₆+x₇= 138.

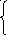2x₁ + 6x₃+11/3x₄+x₅ - x₆/3 = 110

(17) x₂ + 4/3x₄ +x₆/3= 30

3x₁+ 4x₃- 8/3x₄ -2/3x₆+x₇= 138.

Приравняв к нулю свободные переменные х₁, х₃, х₄, х₆, получаем базисное неотрицательное решение, совпадающее с (9), причем первые четыре компоненты его определяют новую производственную программу

(18) x₁=0,x₂=90/3,x₃=0,x₄=0.

Исследуем, является ли эта программа наилучшей, т.е. обеспечивает ли она наибольшую прибыль. Для этого выразим функцию прибыли (1) через новые свободные переменные х₁, х₃, х₄, х₆.

Из второго уравнения системы (17) выражаем базисную переменную х₂через свободные и подставляем в (1). Получаем

z=27x₁+39x₂+18x₃+20х₄

z=27x₁+39(30 - 4/3x₄ -x₆/3)+18x₃+20х₄

z=27x₁+1170-52x₄ - 13 x₆ +18x₃+20х₄

(19) z=1170 + 27x₁ +18x₃ - 32 x₄ - 13 x₆

Видим, что программа (18) не является наилучшей, так как прибыль будет расти, если мы начнем производить или первую, или третью, или четвертую продукцию, но наиболее быстро функция zрастет при возрастании х₁. Поэтому принимаем х₁в системе (17) за разрешающую неизвестную, находим разрешающее уравнение по

(20) Min(110/2; 138/3) = 138/3 - разрешающее ур-ние 3

и исключаем х₁из всех уравнений системы (17), кроме третьего уравнения. Получим следующий предпочитаемый эквивалент системы условий, который определит для системы (4) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого нам придется выразить функцию (19) через новые свободные переменные, удалив оттуда переменную х₁, ставшую базисной. Мы видели выше, как это делается (удаляли х₂из (1)).

Важно обратить внимание на то, что эти удаления можно выполнить очень просто. Представим соотношение (1) в виде уравнения

(21) -27x₁-39x₂-18x₃-20х₄=0-z

и припишем его к системе (4). Получается вспомогательная система уравнений

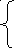
2x₁ + 1x₂ + 6x₃ + 5x₄ + x₅ = 140

(22) 3x₂ + 4x₄ + x₆ = 90

3x₁+ 2x₂ + 4x₃ + x₇ = 198

-27x₁-39x₂-18x₃-20х₄ =0-z

Напомним, что разрешающую неизвестную в системе (4) мы выбрали х₂. Этой переменной в последнем уравнении системы (22) отвечает наименьший отрицательный коэффициент₂= -39. Затем мы нашли разрешающий элемент а₂₂=3 и исключили неизвестную х₂из всех уравнений системы (4), кроме второго. Далее нам пришлось х₂исключать и из функции (1). Теперь это можно сделать очень просто, если посмотреть на систему уравнений (22). Очевидно, достаточно умножить второе уравнение системы (22) на 13 и прибавить к четвертому; получим

3x₂ + 4x₄ + x₆ = 90 | *13 |_2/ разрешающий элемент а₂₂|=13

39x₂ + 52x₄ + 13x₆ = 1170

23. -27x₁ - 18 x₃ + 32 x₄+ 13x₆ = 1170 - z

Таким образом, мы преобразовывали вспомогательную систему уравнений (22) к виду

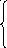2x₁ + 6x₃ + 11/3x₄ + x₅ - x₆/3 = 110

(24) x₂ + 4/3x₄ + x₆/3 = 30

3x₁ + 4x₃ - 8/3x₄ - 2/3 x₆ + x₇ = 138.

-27x₁ - 18 x₃ + 32 x₄+ 13x₆ = 1170 - z

Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент (17) системы уравнений (4) и определяют базисное неотрицательное решение (9) и производственную программу (18), а из последнего уравнения системы (24) получается выражение (19) функции цели через свободные переменные. Очевидно, если имеется хотя бы один отрицательный коэффициент _jпри какой-нибудь переменнойx_jв последнем уравнении системы (24), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. С помощью (19) мы выяснили, что следует начинать производить продукцию первого вида, т.е. фактически мы нашли в последнем уравнении системы (24) наименьший отрицательный коэффициент

min(_j<0) = min(-27, -18) = -27 = ₁

и решили перевести свободную переменную х₁в число базисных, для чего, согласно (20) определили разрешающее уравнение и указали разрешающий элемент а₃₁=3.

У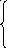читывая сказанное выше, теперь мы будем преобразовывать не систему (17), а всю вспомогательную систему (24), по формулам исключения. Эта система преобразуется к виду

2x₁ + 6x₃+ 11/3x₄+x₅ - x₆/3 = 110

x₂ + 4/3x₄ +x₆/3= 30

3x₁+ 4x₃- 8/3x₄ -2/3x₆+x₇= 138 - разрешающее ур-ние

-27x₁ - 18 x₃ + 32 x₄+ 13x₆ = 1170 - z

3x1 + 4x3 – 8/3x4 – 2/3x6 +x7 = 138 | :3

x1 + 4/3x3 – 8/9x4 – 2/9x6 + 1/3x7 = 46 | *2

2x1 + 8/3x3 – 16/9x4 – 4/9x6 + 2/3x7 = 92

Из 1-ого вычитаем полученное:

2x₁ + 6x₃+ 11/3x₄+x₅ - x₆/3 = 110

-

2x1 + 8/3x3 – 16/9x4 – 4/9x6 + 2/3x7 = 92

10/3х3+49/9х4+х5+1/9х6-2/3 х7=18

x1 + 4/3х3– 8/9x4 – 2/9x6 + 1/3x7 = 46 | *(-27)

-27х1-108/3х3+216/9х4+54/9х6-27/3х7=-1242

-27х1-36х3+24х4+6х6-9х7=-1242

Из 4-ого вычитаем полученное:

-27x₁ - 18 x₃ + 32 x₄+ 13x₆ = 1170 - z

-

-27х1 - 36х3 + 24х4 +6х6-9х7 =-1242

18х3 + 8х4 +7х6 + 9х7 = 2412 – z

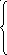
10/3х3 + 49/9х4+х5+1/9х6-2/3 х7 = 18

x₂ + 4/3x₄ +x₆/3= 30 (25)

x1 + 4/3x3 – 8/9x4 –2/9x6 + 1/3x7 = 46

18х3 + 8х4 +7х6 + 9х7 = 2412 – z

x1=46; x2=30; x3=0; x4=0; x5=18; x6=0; x7=0, (26)

т.е. определяют производственную программу

x1=46;x2=30;x3=0;x4=0 (27)

и остатки ресурсов:

первого вида х₅=0

второго вида х₆=13 (28)

третьего вида х₇=0

В последнем уравнении системы (25) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели zчерез остальные неотрицательные переменные

Z= 2412 - 18х3 - 8х4 - 7х6 - 9х7 (29)

то становится совершенно очевидным (в силу того, что все x_j0), что прибыль будет наибольшей тогда, когда

x3=0;x4=0;x6=0;x7=0. (30)

Это означает, что производственная программа (27) является наилучшей и обеспечивает предприятию наибольшую прибыль

z_max= 2412 (31)

Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.

Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.

Таблица 1

			27 39 18 20 0 0 0	Пояснения
	Базис	Н	x1 x2 x3 x4 x5 x6 x7
0	х5	140	2 1 6 5 1 0 0	z0 = H
0	х6	90	0 3 0 4 0 1 0
0	х7	198	3 2 4 0 0 0 1	Min(j<0)=-39
	z0 -z	0-z	-27 -39 -18 -20 0 0 0	Min (bi/ai2>0)=90/3
0	х5	110	2 0 6 11/3 1 -1/3 0	Min(-27, -18)=-27
39	х2	30	0 1 0 4/3 0 1/3 0
0	х7	138	3 0 4 -8/3 0 -2/3 1	Min (110/2; 138/3)= 138/3
	z0 -z	1170-z	-27 0 -18 32 0 13 0
0	х5	18	0 0 10/3 49/9 1 1/9 –2/3
39	х2	30	0 1 0 4/3 0 1/3 0	все j 0
27	х1	46	1 0 4/3 -8/9 0 -2/9 1/3
	z0 -z	2412-z	0 0 18 8 0 7 9

где представлены расширенные матрицы вспомогательных систем уравнений (22) (24)(25). Эти таблицы принято называть симплексными.

Проверим получившийся результат.

Воспользуемся тем, что в оптимальной производственной программе х₃=0, х₄=0. Предположим, что третью и четвертую продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:

_{X (x1, x2) - ?}

_{Z = 27x1 + 39x2  max}

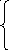
2 x₁+ 1x₂≤140

2 x₂≤90

3 x₁+ 2x₂≤198

x₁  0, x₂  0

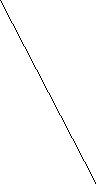
Х2

|||

||М

30

|

046 6670

Х1

Точка М находится на пересечении || и ||| линий.

2 x₂=90

3 x₁+ 2x₂=198

х2=30; 3х1+60=198, х1=46.

Из графика видно, что результаты совпадают.

Обращенный базис, отвечающий оптимальной производственной программе, содержится в последней симплексной таблице:

Обращенный базис Q^-1

1 1/9 -2/3

Q^-1= 0 1/3 0

0 -2/9 1/3

х₅ х₆ х₇

Для того, чтобы убедиться в правильности полученного решения, следует проверить отношение Н = Q^-1 * В:

1*140+1/9*90-2/3*198 18

Q^-1 •B= 0*140+1/3*90+0*198 = 30

0*140-2/9*90+1/3*198 46