
- •Міністерство освіти і науки, молоді та спорту України
- •Програма курсу
- •Предмет диференціальної геометрії. Історичний огляд розвитку диференціальної геометрії
- •Тема 1. Вектор-функція скалярного аргументу
- •1.1. Операції над сталими векторами та їх застосування
- •1.2. Вектор-функція скалярного аргументу
- •1.3. Границя вектор-функції
- •1.4. Неперервність вектор-функції
- •1.5. Похідна вектор-функції
- •1.6. Формула Тейлора
- •1.7. Інтеграл від вектор-функції
- •1.8. Вектор сталої довжини
- •Контрольні питання до теми 1
- •Тема 2. Поняття кривої. Регулярна крива і способи її задання
- •2.1. Поняття кривої
- •2.2. Способи аналітичного задання просторової кривої
- •2.3. Випадок плоскої кривої
- •Контрольні питання до теми 2
- •Перелічіть способи аналітичного задання просторової кривої. Запишіть відповідні рівняння. Які умови є достатніми для того, щоб ці рівняння визначали регулярну криву?
- •Тема 3. Дотична пряма і супровідний тригранник кривої
- •3.1. Дотична пряма просторової кривої
- •3.2. Нормальна площина просторової кривої
- •3.3. Дотична і нормаль плоскої кривої
- •3.4. Стична площина кривої
- •3.5. Супровідний тригранник кривої
- •Контрольні питання до теми 3
- •Тема 4. Поняття теорії кривих, пов’язані з поняттями кривини та скруту
- •4.1. Довжина дуги кривої. Натуральна параметризація
- •4.2. Кривина кривої, заданої в натуральній параметризації
- •4.3. Кривина кривої в довільній параметризації
- •4.4. Кривина плоскої кривої
- •4.5. Скрут кривої, заданої в натуральній параметризації
- •4.6. Скрут кривої в довільній параметризації
- •4.7. Формули Френе
- •1. ; 2.; 3..
- •Контрольні питання до теми 4
- •Список використаної та рекомендованої літератури
- •Додаток 1 Питання для підготовки до вхідного контролю з навчальної дисципліни «Диференціальна геометрія та топологія»
- •Додаток 2
- •Завдання вхідного контролю з навчальної дисципліни
- •«Диференціальна геометрія та топологія»
- •Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
- •Додаток 3 Тестовий контроль з теорії кривих Тест 1. Вектор-функція скалярного аргументу
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •2. Вставити пропущені слова так, щоб одержалось правильне твердження.
- •Тест 2. Поняття кривої. Регулярна крива і способи її задання
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •Тест 3. Дотична пряма і супровідний тригранник кривої
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •Пов’язані з поняттями кривини та скруту
- •1. Вказати правильні відповіді із запропонованих.
- •2. Вставити пропущені слова так, щоб одержалось правильне твердження.
- •Зоря Валентина Дмитрівна,
4.3. Кривина кривої в довільній параметризації
Нехай
криву задано векторним рівнянням
![]() .
Довжина дугиs
є функцією параметра
.
Довжина дугиs
є функцією параметра
![]() :
:![]() ,
отже
,
отже![]() є
складеною функцією
є
складеною функцією
![]() .
Знайдемо другу похідну від
.
Знайдемо другу похідну від![]() поs
через похідні по t.
поs
через похідні по t.
Для
зручності домовимося похідні вектор-функції
по натуральному параметру s
позначати
з крапкою (![]() ,
,![]() і т.д.), а похідні подовільному
параметру t
– зі штрихом (
і т.д.), а похідні подовільному
параметру t
– зі штрихом (![]() ,
,![]() і т.д.).
і т.д.).
![]() ; (14)
; (14)
![]() ,
звідки
,
звідки
![]() . (15)
. (15)
З
(14) маємо:
![]() , причому
, причому![]() .
.
Враховуючи,
що
![]() ,
одержимо
,
одержимо![]() .
.
Підставимо
одержані вирази для
![]() ,
,![]() ,
,![]() в
(15):
в
(15):
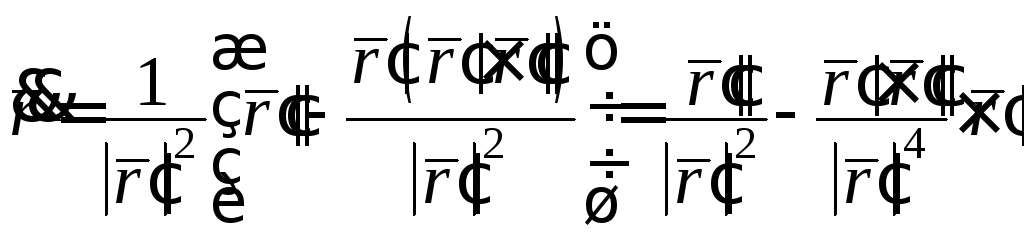 .
.
Для
обчислення кривини
![]() знайдемо
знайдемо![]() .
.
Оскільки
![]() – одиничний вектор і його похідна
– одиничний вектор і його похідна![]() ортогональна
ортогональна![]() ,
то
,
то![]() можна знайти як модуль векторного
добутку
можна знайти як модуль векторного
добутку![]() :
:![]() .
.
 .
.
 (16)
(16)
В скалярній формі маємо:
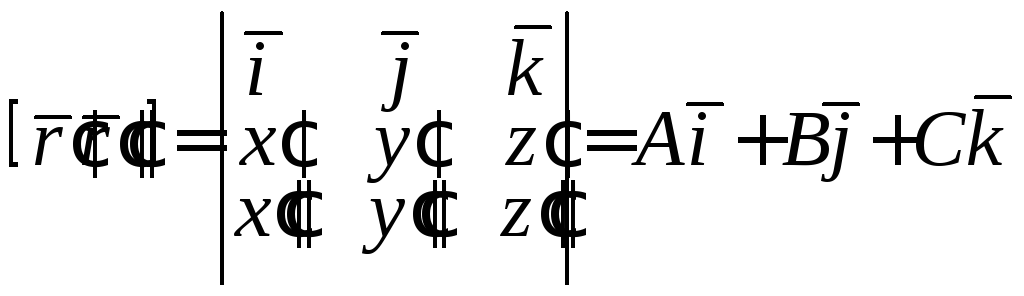 ,
де A,
B,
C
– координати вектора
,
де A,
B,
C
– координати вектора
![]() ,
тобто
,
тобто
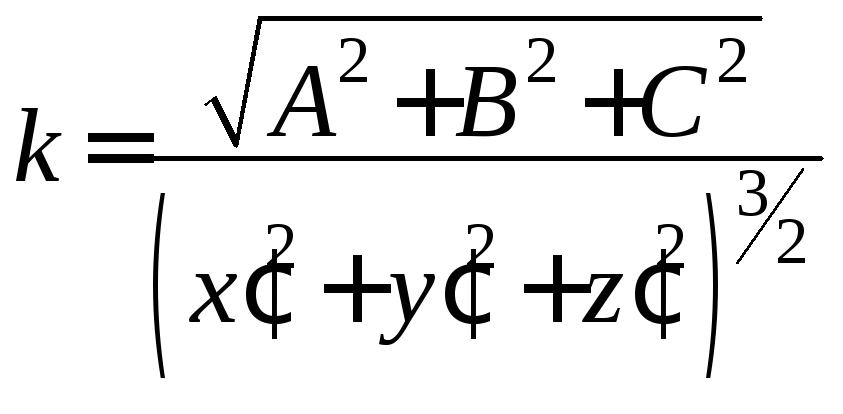 (16')
(16')
Задача.
Знайти кривину гвинтової лінії
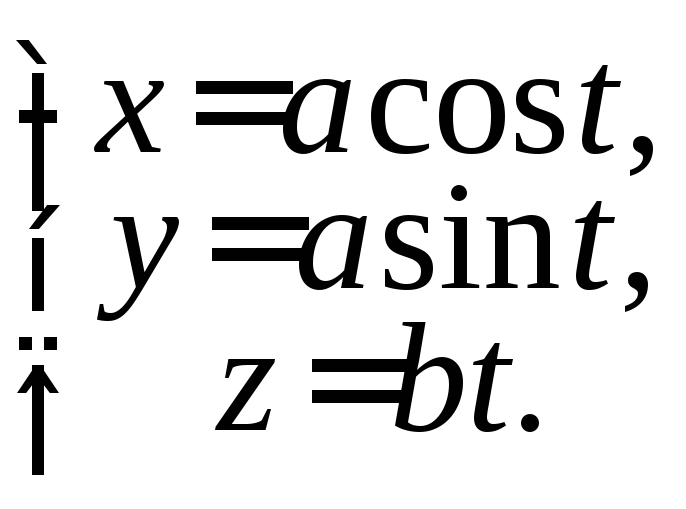
Розв’язання.
![]()
![]()
![]()
![]()
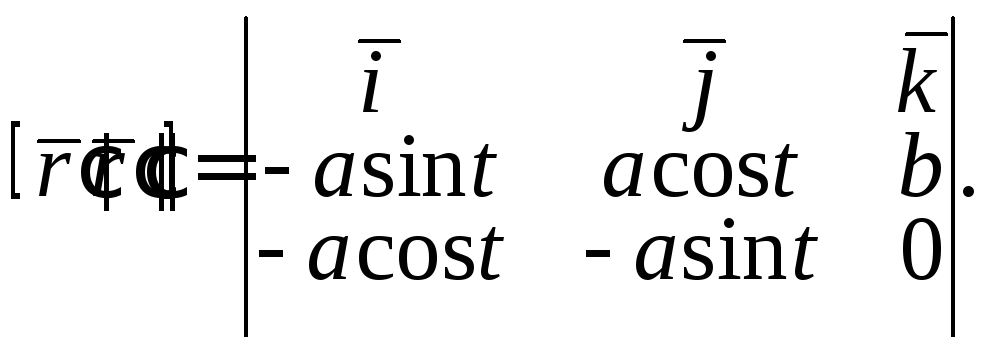
Отже
![]() ;
;![]() ;
;![]() ;
;
![]() .
.
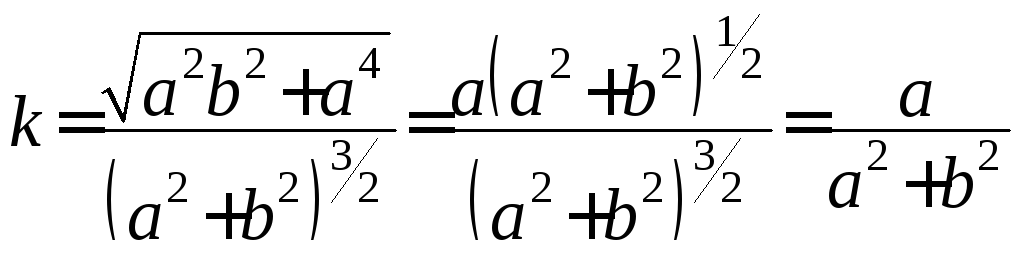
Таким чином, кривина гвинтової лінії є сталою величиною.
Відповідь:
![]() .
.
4.4. Кривина плоскої кривої
З формул (16) і (16') легко одержати формули для обчислення кривини плоскої кривої:
1)
 :
:
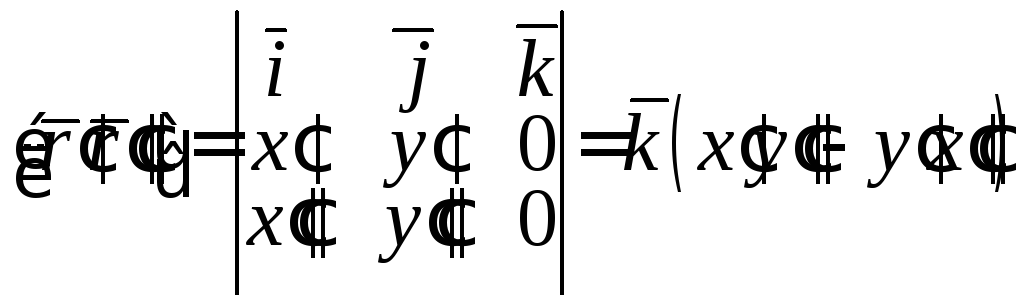 ;
;
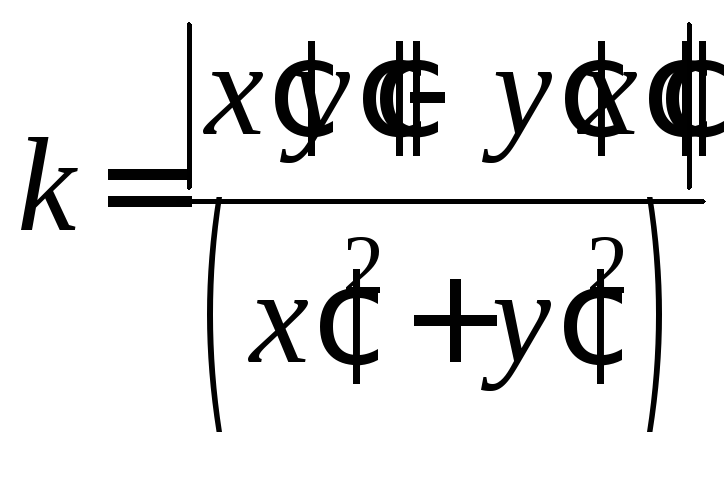 . (17)
. (17)
2)
![]() :
:
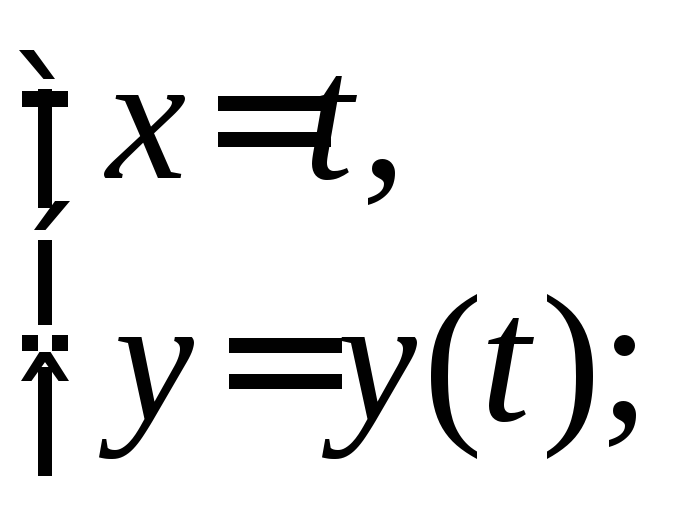
![]()
![]()
![]()
 . (17')
. (17')![]()
3)
![]() :
вважаємо щоy
є функцією від x,
диференціюємо дане рівняння по x
, звідки
:
вважаємо щоy
є функцією від x,
диференціюємо дане рівняння по x
, звідки
![]() і
і
![]() ; далі знаходимо
; далі знаходимо
![]() і підставляємо у формулу (17').
і підставляємо у формулу (17').
|
Для
плоскої кривої можна визначити кривину
|
4.5. Скрут кривої, заданої в натуральній параметризації
Кривина кривої є кількісною мірою відхилення кривої від прямої, а саме: від дотичної прямої.
Скрут – це кількісна міра відхилення кривої від площини, а саме: від стичної площини. Таким чином, скрут вказує наскільки крива відрізняється від форми плоскої кривої.
Положення
стичної площини визначається нормальним
вектором бінормалі
![]() .
Швидкість зміни положення
.
Швидкість зміни положення![]() характеризує скрут кривої аналогічно
до того, як швидкість зміни вектора
дотичної характеризує кривину.
характеризує скрут кривої аналогічно
до того, як швидкість зміни вектора
дотичної характеризує кривину.
Н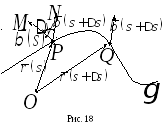 ехайP
– довільна
точка
кривої
ехайP
– довільна
точка
кривої
![]() ,Q
–
точка
,Q
–
точка
![]() ,
близька доP.
Очевидно,
що величина двогранного кута між стичними
площинами в точках P
і Q
дорівнює величині кута між бінормалями
в цих точках.
,
близька доP.
Очевидно,
що величина двогранного кута між стичними
площинами в точках P
і Q
дорівнює величині кута між бінормалями
в цих точках.
Позначимо:
![]() кут
між бінормалями в точках P
і Q;
кут
між бінормалями в точках P
і Q;
![]() s
– довжина дуги PQ
кривої
s
– довжина дуги PQ
кривої
![]() .
.
|
Абсолютним
скрутом
|
|
Теорема
9.
Регулярна крива класу
де
|
□ Розглянемо
властивості![]() вектора
вектора
![]() :
:
1)![]() (бо
(бо
![]() – одиничний вектор, отже
– одиничний вектор, отже![]() ,
,![]() );
);
2)
![]() (оскільки
(оскільки
![]() ,
з першої формули Френе (13):
,
з першої формули Френе (13):![]() і
і
![]() ); (19)
); (19)
3)
отже
![]() ,
тому
,
тому
![]() .
Візьмемо в цій рівності знак мінус:
.
Візьмемо в цій рівності знак мінус:
![]() .
.
![]() (третя
формула Френе). (20)
(третя
формула Френе). (20)
Таким
чином
![]() .
.
Знайдемо
тепер
![]() .
.![]() ,
,![]() або
або![]() .
.
Враховуючи (19), (13) і розглядаючи кривину k як функцію s , маємо:
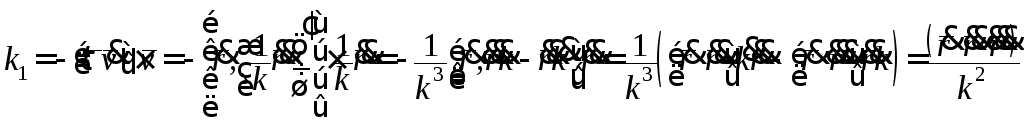 .
.
Отже,
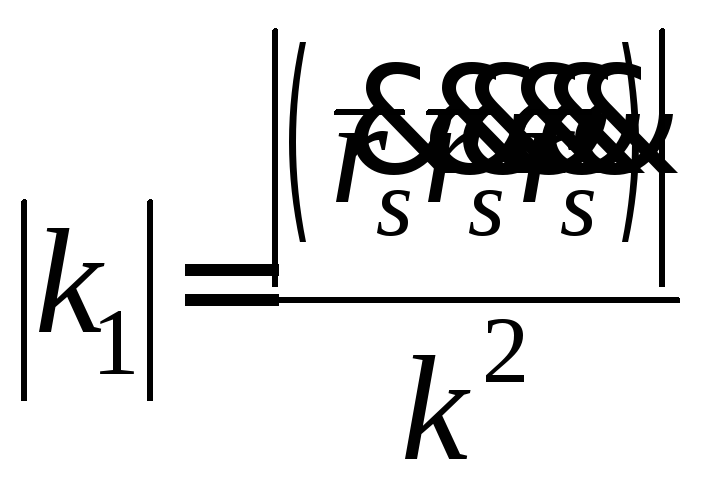 .■
.■
4.6. Скрут кривої в довільній параметризації
Нехай
![]() .
Будемо вважати, що
.
Будемо вважати, що![]() і
і![]() .
Як і в знаходженні кривини, похідні
вектор-функції по натуральному параметруs
будемо позначати з крапкою (
.
Як і в знаходженні кривини, похідні
вектор-функції по натуральному параметруs
будемо позначати з крапкою (![]() ,
,![]() і т.д.), а похідні по довільному параметруt
зі штрихом
(
і т.д.), а похідні по довільному параметруt
зі штрихом
(![]() ,
,![]() і т.д.).
і т.д.).
Для
натуральної параметризації маємо:
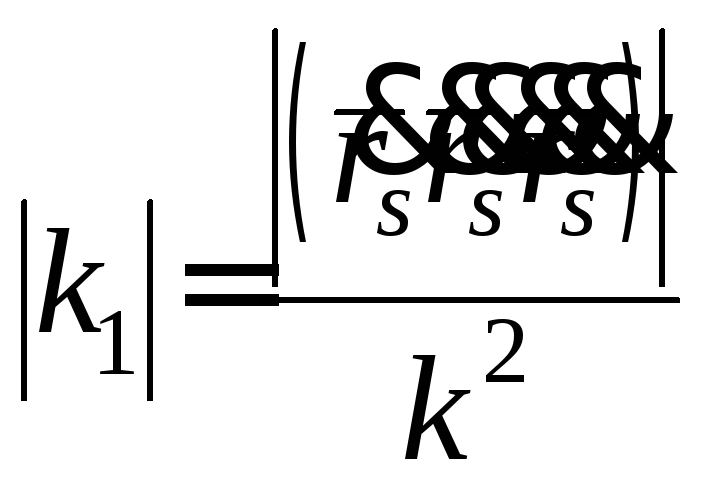 .
.
Виразимо
похідні
![]() ,
,![]() ,
,![]() поs
через похідні
поs
через похідні
![]() ,
,![]() ,
,![]() по параметруt
.
по параметруt
.
Раніше
було показано, що
![]() ;
;![]() .
.
Для
знаходження
![]() використаємо отриману вище в пункті
4.3 формулу:
використаємо отриману вище в пункті
4.3 формулу:![]() .
Тоді
.
Тоді![]() ,
звідки
,
звідки![]() .
.
Нагадаємо,
що для довільної параметризації
![]() ,
,![]() ,
, ,
тому
,
тому .
.
Таким
чином,
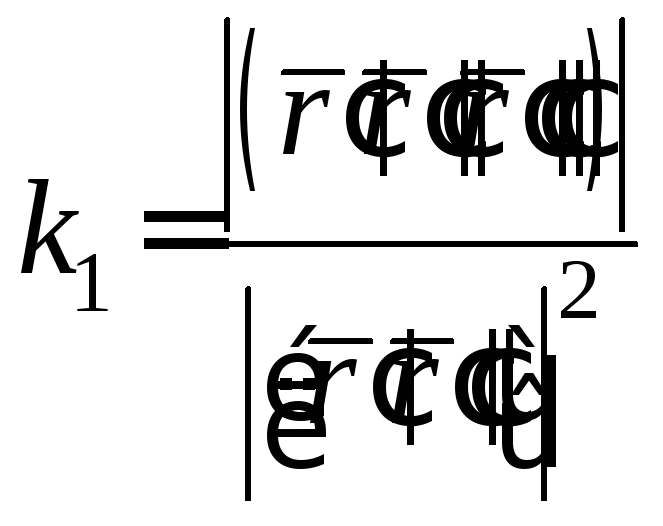 – абсолютний скрут в довільній
параметризації.
– абсолютний скрут в довільній
параметризації.
Скрутом
кривої називається величина ![]() ,
яка обчислюється за формулою:
,
яка обчислюється за формулою:
 . (21)
. (21)
В
скалярній формі:
 (21')
(21')
Зауваження. Плоскі криві – це криві нульового скруту.
Задача.
Знайти скрут гвинтової лінії

Розв’язання.


![]()
 .
.
![]() .
.
Мішаний
добуток
![]() обчислимо як скалярний добуток
обчислимо як скалярний добуток![]() і
і![]() :
:
![]() .
.
Тоді
![]() .
.
Таким
чином, скрут гвинтової лінії є сталою
величиною. Якщо
![]() – «правогвинтова нарізка»; якщо
– «правогвинтова нарізка»; якщо![]() – «лівогвинтова».
– «лівогвинтова».
Відповідь:
![]() .
.

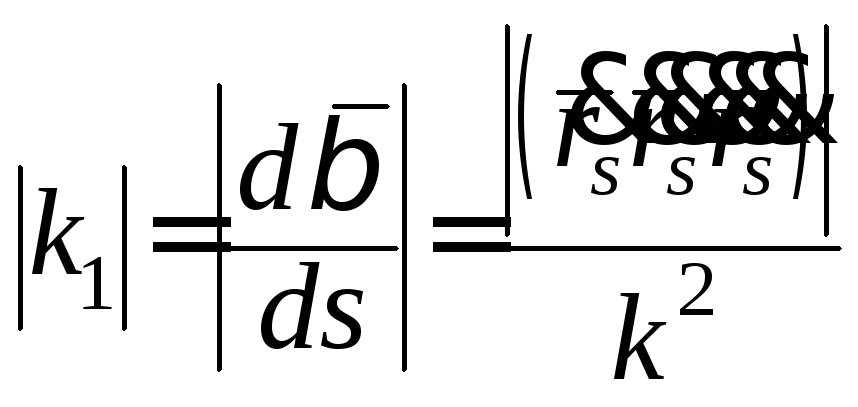 ,
(18)
,
(18)