Лекція 9

Різні способи задання прямої та площини в просторі.

План.

1. Геометричні образи рівнянь першого степеня з трьома змінними.

2. Різні способи задання площини.

3. Загальне рівняння площини та його частинні випадки.

4. Різні способи задання прямої в просторі.

5. Задачі.

1. Рівняннявизначає в просторі деяку поверхню. Розглянемо випадок, коли це рівняння першого степеня відносно зміннихта, тобто записується у виді

, (1)

де - деякі числові коефіцієнти, які одночасно не рівні нулю,- довільне число.

Покажемо, що це рівняння визначає в просторі деяку площину. Нехай у рівнянні (1)та– один із розв’язків цього рівняння. Введемо в розгляд два неколінеарні векторитата відкладемо їх від точки. Нехайта. Тоді точкитаматимуть наступні координати:. Переконаємось у тому, що одержані точки належать поверхні (1).

Підставляючи координати точки у рівняння (20), дістаємо

_,

тобто точка належить поверхні. Аналогічні обчислення виконуються для точки. Нехай– довільний розв’язок (1) а- відповідна точка на поверхні. Тоді векторитабудуть компланарними. Справді, обчисливши їх мішаний добуток, дістаємо

.

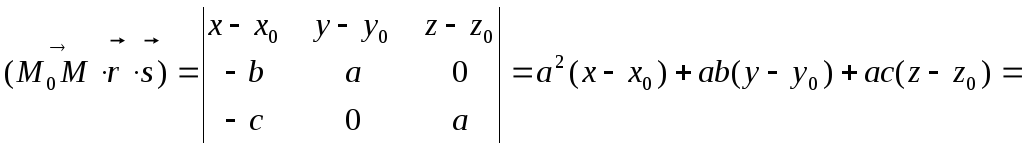
Оскільки вектори компланарні , то точки талежать в одній площині, що і потрібно було довести.

2.Складемо рівняння площинив довільній афінній системі координату тому випадку, коли вона задається перетином двох прямих.

Нехай - спільна точка цих прямих, а неколінеарні векторитазадають їхні напрямки (рис. 1). Точканалежатиме площині, визначеній даними прямими, тоді і тільки тоді, коли векторитабудуть компланарними, тобто коли їхній мішаний добуток дорівнюватиме нулю.

З умови дістаємо рівність

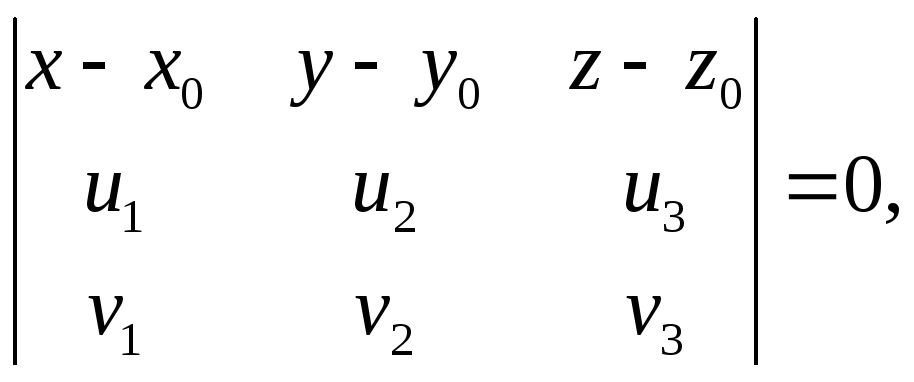(2)

яка і є шуканим рівнянням площини. Рівняння (2) можна записати у виді (1). У цьому випадку ,,.

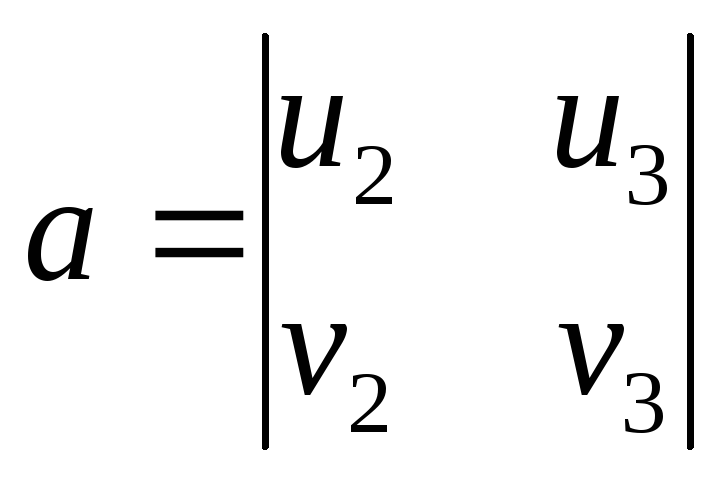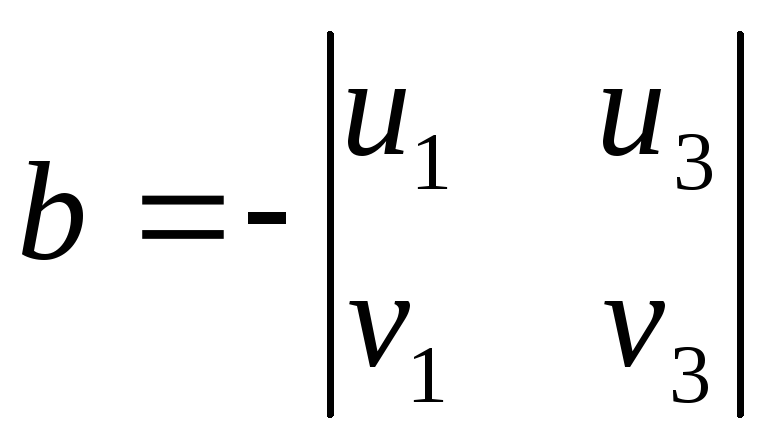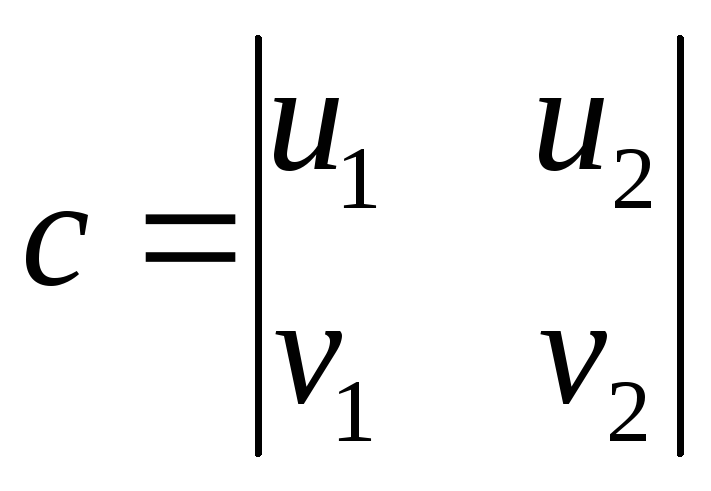Нехай площина задана трьома точками , які не лежать на одній прямій. Тоді, скориставшись рівнянням (2), в якому покладемо

,,

а замість точки використаємо точку, дістанемо рівняння

. (3)

Одержане співвідношення називають рівнянням площини, яка проходить через три заданіточки.

Нехай площинавідтинає на осяхвідрізкивідповідно ( рис.2). У цьому випадку для того, щоб скласти рівняння площини, введемо в розгляд точкита скористаємось попереднім результатом. Дістаєм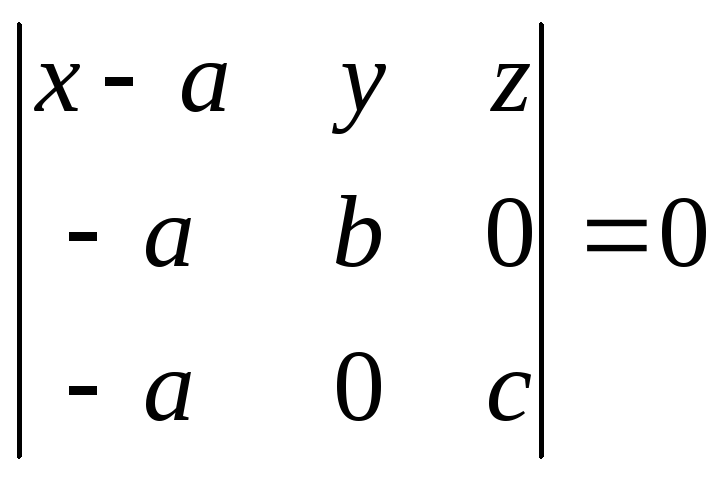о, абозвідки

(4)

Одержане рівняння називають рівнянням площини у відрізках на осях.

Нехай задана прямокутна декартова система координат . Розглянемо деяку площинуіз заданою на ній точкоюта векторомякий перпендикулярний до площини (рис.3). Точканалежатиме площині тоді і тільки тоді, коли векторитабудуть перпендикулярними, тобто коли виконується умова. Обчисливши координати вектората скалярний добуток, отримаємо рівність

. (5)

Одержане рівняння є рівнянням площини, яка проходить через задану точку, перпендикулярно до даного напрямку. Порівнявши рівності (1) та (5), можна зробити наступний висновок: в прямокутній декартовій системі координат коефіцієнти біля зміннихтау рівнянні площини визначають вектор ,якийперпендикулярний до площини.

3.Рівняння (1), до якого зводяться рівняння площини в усіх розглянутих випадках, називають загальним рівнянням площини. Розглянемо особливості розташування площини (1) відносно системи координат у випадках, коли деякі з коефіцієнтів рівні нулю. При цьому будемо користуватись наступною лемою.

Лема. Для того, щоб векторбув паралельним до площини, заданої рівнянням, необхідно та достатньо, щоб виконувалася рівність

. (6)

Доведення.Нехай векторпаралельний до площини, а також точкає початком вектора. Тоді точка, для якої, теж належить площині, а її координати задовольняють рівняння площини. Тому

. Навпаки, нехай виконується рівністьВізьмемо на площинідовільну точкута розглянемо точкутаку, що. Тоді точканалежать площині, в чому легко переконатися, підставивши її координати в рівняння площини. Отже, векторпаралельний площині.

Перейдемо до розгляду частинних випадків рівняння (1).

1. Нехай , тобто рівняння площинимає виглядОчевидно, що- розв’язок рівняння, отже, площина проходить через початок координат.

2. Нехай. Тоді рівняння площини набуває виду. Розглянемо вектор, паралельний до осі. Згідно з доведеною лемою він паралельний до площини, тому у цьому випадку площина паралельна до осі(рис. 1). Аналогічні висновки робимо прита. Тобто площина, задана рівняннямпаралельна до осі, а площина, задана рівнянням, паралельна до осі. Якщоабо, то площина проходить через вісь(відповідно через вісьабо вісь).

3

. У випадку, коли, рівняння площининабуває видуабо, де. Тоді площина, будучи паралельною до осей та, буде паралельною до площини(рис. 2). Прирівнянняє рівнянням площини. Аналогічно, якщо, то рівняннязадає площину, яка паралельна до площини(). Рівняннятає рівняннями площинтавідповідно.

4.У загальній афінній системі координатрозглянемо пряму, задану точкоюта напрямним вектором. Нехай- довільна точка цієї прямої. Очевидно, що точканалежить прямійтоді і тільки тоді, коли векторитаколінеарні. Із пропорційності їхніх координат дістаємо співвідношення

, (7)

яке називають канонічним рівнянням прямої в просторі. Прирівнявши одержані відношення до параметра, дістаємо

(8)

Одержані рівняння називають параметричними рівняннями прямої в просторі. Їх використовують, наприклад, у випадку, коли деякі з чиселу рівнянні (7) рівні нулю.

Аналогічно до параметричних рівнянь прямої на площині (див. лекцію.7. п.2), параметр має свій геометричний зміст, а саме: якщо вектор- одиничний, тобто якщо, тодорівнює відстані від точкидо точки. Це дає можливість легко знаходити на прямій точки, розташовані на певній відстані від заданої точки. Наприклад, нехай задана пряма, до якої паралельний вектор, а, отже, і його орт. Задамо пряму рівняннями,,. Тепер, щоб знайти на прямій точки, розташовані від точкина певній відстані, нехай на відстані 6, достатньо в одержані рівняння прямої підставити. Одержимо дві точкитакі, що

Нехай пряма проходить через дві точки . Тоді, скориставшись рівнянням прямої у виді (7) та замінивши в ньому координати точкикоординатами точкиі використавши вектор у ролі напрямного вектора, дістанемо

(9)

Одержане співвідношення називають рівнянням прямої в просторі, що проходить через дві задані точки.

У деяких випадках пряму в просторізручнозадавати, як лінію перетину двохплощин, тобто у виді системи рівнянь

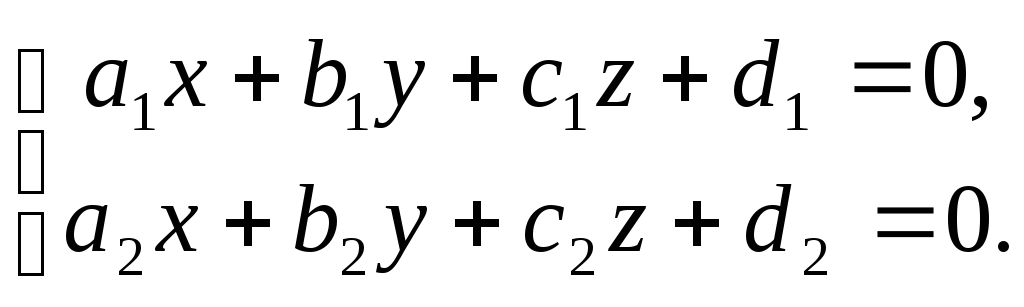(10)

При цьому для того, щоб площини перетиналися, будемо вимагати непропорційності коефіцієнтів біля змінних в заданих рівняннях. Перехід від задання прямої у виді (10) до виду (7) або (8) можна здійснювати, знайшовши, наприклад, два довільні розв’язки системи (10), або знайшовши координати напрямного вектора прямої, який можна одержати, як векторний добуток векторів нормалей до даних площин. Нагадаємо, що координати цих векторів є коефіцієнтами біля змінних у заданих рівняннях.

Зробимо ще одне зауваження. Рівність (7) можна записати у вигляді однієї із трьох систем

;;.

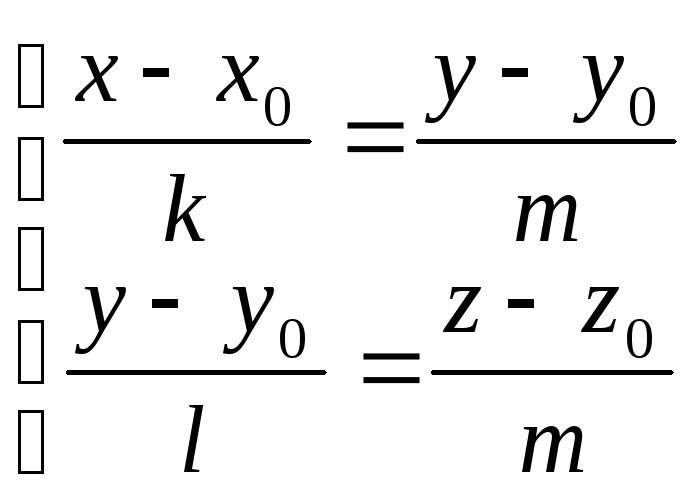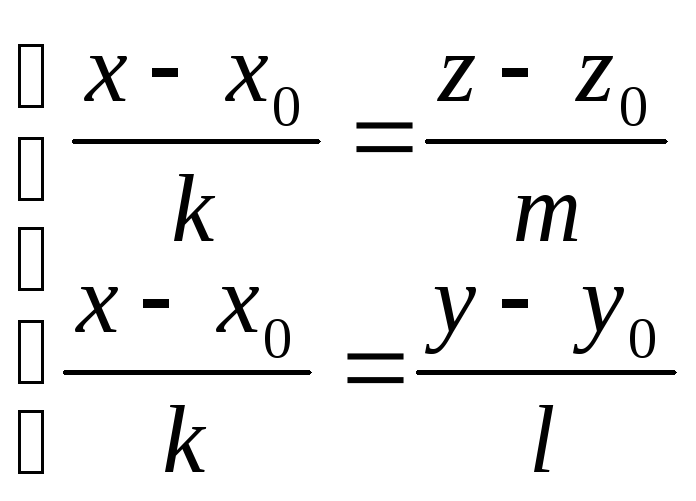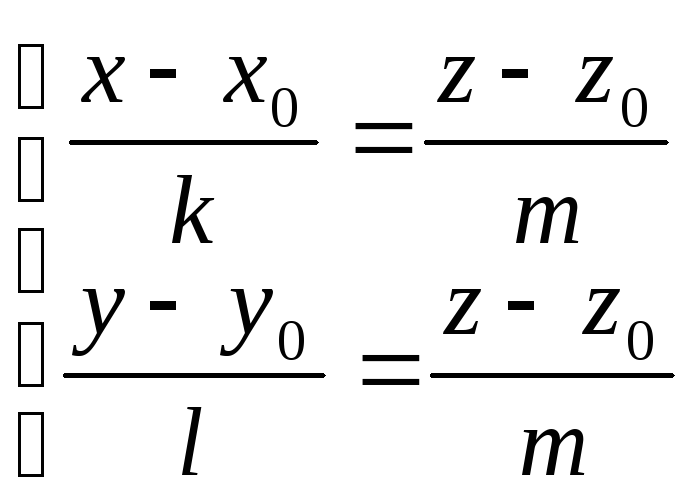Кожне з рівнянь систем є рівнянням першого степеня, тому є рівнянням площини, а відсутність однієї змінної в кожному рівнянні говорить про паралельність відповідної площини до певної координатної осі. Тому канонічне рівняння прямої (7) фактично задає пряму, як перетин трьох площин, кожна з яких паралельна до певної координатної осі.

5.Розглянемо приклади розв’язання задач.

Задача 1. Зобразити лінію перетину площинта.

Розв’язання.Зобразимо площину. Для цього знайдемо точкитаїї перетину з осямита. Оскільки||(в рівнянні площини відсутня змінна), то, провівши через точкитапрямітапаралельно до осі, дістанемо зображення площини. На осізнаходимо точку, яка належить площині, і через неї проводимо пряміта. Точкаі прямітавизначають площину. Точкаперетину прямихтаналежить шуканій прямій перетину площин, оскільки обидві прямі лежать в одній площині (площині) і перетинаються. Аналогічно, точкаперетину прямихта, які лежать в площині, теж належить лінії перетину. Таким чином, шуканою прямою є пряма(рис. 3).

Задача 2.Скласти рівняння ортогональної проекції прямої, заданої канонічним рівняннямна площину, задану рівнянням^.

Розв’язання.Скористаємось векторомякий перпендикулярний до площинита вектором, який паралельний до прямої. Дані вектори не колінеарні, тому прямане перпендикулярна до, отже її проекцією буде деяка пряма. Другу площину, якій належитьs, проведемо через пряму, перпендикулярно до. Очевидно, що площинапроходить через точку, яка належить прямійі паралельна до векторівта. Скориставшись рівнянням (2), дістаємо рівняння площин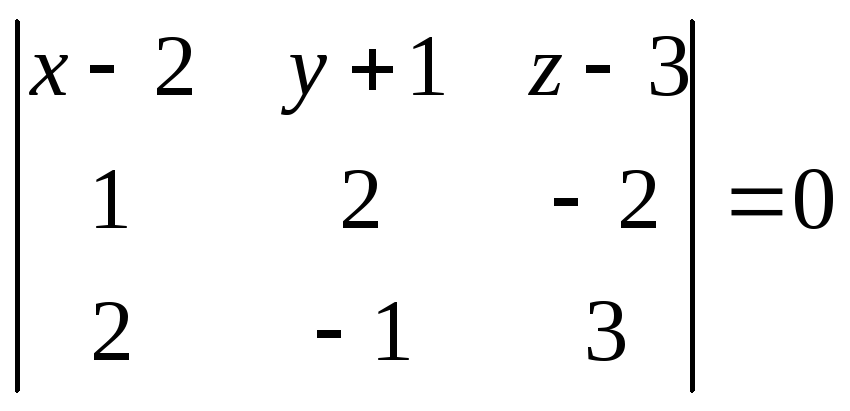и:, звідки, або, остаточно, Шукане рівняння прямої подамо у виді (10), як перетин площинта.

Відповідь:

Задача 3. Три грані куба з ребром 1 належать координатним площинам. Побудувати переріз куба площиною .

Розв’язання.Зобразимо заданий кубта площину, побудувавши на осях точки

(рис. 4). Знаходимо точкуперетину прямихта(обидві прямі лежатьуплощині) та точкуPперетину прямихта. ПрямаPNлежить у площиніта в площиніі перетинає ребра верхньої грані куба в точкахRтаS. Тепер знаходимо точкуперетину прямихтаі проводимо пряму, яка перетне реброу деякій точціT.

Відповідь: трикутник .