
- •3.Варіанта-змінна.
- •4. Нескінченно малі та нескінченно великі величини.
- •7.Леми про нескінченно малі:
- •12.Класифікація нескінченно великих
- •24. Задачі , які приводять до поняття похідної. Означення похідної.
- •27.Найпростіші правила диференціювання. Похідні оберненої функції. Похідна складеної функції.
- •31 Інваріантність форми диференціалу першого порядку
- •32 Застосування диференціала в наближених обчисленнях
- •35 Похідні вищих порядків від функцій, заданих параметрично
- •36 Формула Тейлора для многочленів та довільних функцій
- •39.Застосування формули Тейлора до наближених обчислень.
- •40. Правило Лопіталя- Бернуллі. Розкриття невизначеності 0/0 та ∞/∞ .
- •43.Екстремуми функції , необхідні умови
- •44.Достатні умови екстремуму , перше правило.
12.Класифікація нескінченно великих
Якщо ліміт х->а y(x)/g(x)=∞ то y(x)-нескін велика вищого порядку а g(x)-нескін велика нижчого порядку. Якщо ліміт х->а y(x)/g(x)до к степеню=б – скінченна то y(x) є нескінченно великою катого порядку по відношенню до g(x). Якщо границя відношень нескін великих не існує то кажуть що такі нескін великі не порівнювані. Якщо ліміт х->а y(x)/g(x)=с – скінченна то кажуть що ці нескінченно великі однакового пордяку.
15. Властивості функцій , що мають границю. Якщо функція f(x) при х->а має границю А, і А>р то всі значення змінної починаючи з якогось місця також будуть більші за р. так само для А менше р. Якщо функція f(x) має границю а при х->а і g(x) має границю б при х->а то і сума f(x)+ g(x)=а+б.
Властивості функцій, що мають границі.
1).
Нехай (х),
g(х)
– функції, для яких існує
 (х)
і
(х)
і
 g(х),
тоді
g(х),
тоді
а)
існує
 (х)+g(х)
та
(х)+g(х)
та
 (х)+g(х)=
(х)+g(х)=
 (х)+
(х)+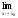 g(х).
g(х).
б)
існує
 (х)g(х)
та
(х)g(х)
та
 (х)g(х)=
(х)g(х)=
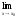 (х)
(х) g(х).
g(х).
в)
для будь-якої сталої С:
 С(х)=С
С(х)=С (х).
(х).
г)
при
 g(х)
існує
g(х)
існує
 (х)g(х)
та
(х)g(х)
та
 (х)g(х)=
(х)g(х)=
 (х)
(х) g(х).
g(х).
2).
Якщо (х)g(х),
то
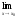 (х)
(х) g(х).
g(х).
3).
Якщо (х)=С,
де С –довільне дійсне число, то
 (х)=С,
тобто границя сталої в довільній точці
х0
дорівнює самій цій сталій.
(х)=С,
тобто границя сталої в довільній точці
х0
дорівнює самій цій сталій.
4). Функція не може мати двох різних границь в одній точці.
16.Границя монотонної варіанти, число е. Варіанта xn називається монотонно зростаючою, якщо x1<x2<x3<…<xn<…
Монотонно спадною,не зростаючою, якщо n’>n=>xn>x’n
n’>n xn>x’n - спадна
n’>n xn≥x’n - не зростаюча
n’>n xn≤x’n – не спадна
Ці 4 типи монотонні.
Якщо змінна xn монотонна і обмежена зверху, то вона має границю М, xn≤М.
Якщо змінна монотонно спадна і обмежена знизу, то вона має скінченну границю xn=(1+1/n)n
Границя lim(1+1/n)n назначена, як число е (Число Ейлера), воно ірраціональне, неперіодичне, е=2,71…
xn – монотонно зростаюча, а yn-монотонно спадна, при чому xn <yn. Якщо їхня різниця xn - yn→0 при зростанні номера n, то обидві варіанти мають спільну границю lim xn= lim yn=c
(c-cпільна точка).
19. Неперервність монотонної функції.
Нехай функція F(x) є монотонно зростаючою на деякій множині Х, при чому цей проміжок може бути як скінченний так і не скінченний, і своїми значеннями заповнює даний проміжок повністю то вона на цьому проміжку неперервна.
Монотонно зростаюча на деякому проміжку Х, F(x) може мати розриви тільки 1-го роду.
Теорема. Елементарна функція є неперервною на своїй області визначення. Основними елементарними функціями є степенева х в степені а показникові а в степені х логарифмічна тригонометрична оберненотригометрична.
Нехай функція F(x) визначена, строго монотонна, зростаюча та неперервна на деякому проміжку Х , тоді на відповідному проміжку У з множини значень функції існує обернена функція, яка також є монотонно зростаюча і неперервна.
20.
Неперервність
складеної функції . Застосування
неперервності до обчислення границь.
Функція у = F(u), де u = j(x), називається
складною (складеною) функцією, або
суперпозицією функцій F(u) та j(х), і
позначається y = F(j (x)).Якщо j(x) неперервна
в точці х=а а функція F(u) неперервна у
відповідній точці j(а) то функція F(j(x))
– неперервна в точці х=а.
Якщо f
неперервна (наприклад
елементарна),
то можна заносити границю в аргумент:
 .Приклад.
.Приклад.
 .
.
Якщо функція Φ(х) неперервна в точці а, а F(x) неперервна в Φ(а), то складена функція F(Φ(x)) неперервна в точці х=а.
Якщо функція U(x) при x→a має границю число А, а функція π(х) при x→a має границю – В, то Uπ(x) має скінченну границю, при чому lim Uπ(x) =AB
23. Перша і друга теорема Вейрштраса. Теорема Кантора та наслідок з неї.
Якщо функція f(x) визначна і неперервна в замкнутому проміжку то вона на цьому проміжку обмежена. Друга теорема Вейєрштраса. Якщо функція f(x) визначна і неперервна в замкнутому проміжку то на цьому проміжку вона досягає свого найбільшого і найменшого значення. Теорема Кантора. Якщо функція f(x) визначена і неперервна в замкнутому проміжку то вона на цьому проміжку рівномірно неперервна.
Наслідок Якщо функція f(x) визначена і неперервна на замкненому проміжку то для Е>0 знайдеться б>0 таке що якщо цей проміжок розбити на відрізки менші з б то коливання функції на кожному з них буде менше за Е.
