
- •3.Варіанта-змінна.
- •4. Нескінченно малі та нескінченно великі величини.
- •7.Леми про нескінченно малі:
- •12.Класифікація нескінченно великих
- •24. Задачі , які приводять до поняття похідної. Означення похідної.
- •27.Найпростіші правила диференціювання. Похідні оберненої функції. Похідна складеної функції.
- •31 Інваріантність форми диференціалу першого порядку
- •32 Застосування диференціала в наближених обчисленнях
- •35 Похідні вищих порядків від функцій, заданих параметрично
- •36 Формула Тейлора для многочленів та довільних функцій
- •39.Застосування формули Тейлора до наближених обчислень.
- •40. Правило Лопіталя- Бернуллі. Розкриття невизначеності 0/0 та ∞/∞ .
- •43.Екстремуми функції , необхідні умови
- •44.Достатні умови екстремуму , перше правило.
24. Задачі , які приводять до поняття похідної. Означення похідної.
Геометричний зміст похідної визначає кутовий коефіцієнт дотичної , а швидкість виражає фізичний зміст похідної.Можна похідну від функції в точці розглядати як швидкість зміни функції в цій точці. Похідною функції f(x) у точці х0 називається границя (якщо вона існує) відношення приросту функції у точці х0 до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x0).
27.Найпростіші правила диференціювання. Похідні оберненої функції. Похідна складеної функції.
28. Односторонні та нескінченні функції.
Якщо т Х0 є лівим чи правим кінцем відрізка то говорячи про похідну як про границю відношення приросту функції до приросту аргументу матимемо на увазі що в першому випадку приріст аргумента має бути додатнім а в другому від’ємним.Тобто буде йти мова про односторонні похідні.Якщо границя відношення приросту функції до приросту аргументу існує але рівна 00 в такому випадку говорять про нескінченні похідні.В такому випадку дотична до кривої вертикальна.
31 Інваріантність форми диференціалу першого порядку
Для
диференційовної функції ![]()
![]() ,
причому
,
причому![]() для
незалежної змінної
для
незалежної змінної![]() .
.
Нехай
функції ![]() та
та![]() -
диференційовні і задають складну
функцію
-
диференційовні і задають складну
функцію![]() .
Тоді
.
Тоді![]() ,
але
,
але![]() .
Тому
.
Тому![]() ,
де
,
де![]() -
диференціал функції
-
диференціал функції![]() .
.
Отже,
диференціал першого порядку зберігає
свою форму, тобто диференціал першого
порядку має один і той же вигляд, який
не залежить від того чи ![]() -
незалежна змінна чи функція.
-
незалежна змінна чи функція.
На основі цієї властивості маємо наступні правила для обчислення диференціалу першого порядку:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
32 Застосування диференціала в наближених обчисленнях
З
означення похідної функції в
точці ![]() випливає,
що її приріст
випливає,
що її приріст![]() можна
подати у вигляді:
можна
подати у вигляді:![]() ,
де
,
де![]() ,
якщо
,
якщо![]() .
.
Отже,
при малих ![]() має
місце наближена рівність:
має
місце наближена рівність:
![]() ,
тобто
,
тобто ![]() .
.
Звідки
![]() .
(3.12)
.
(3.12)
Формула
(3.12) дозволяє знаходити значення
функції ![]() в
точці
в
точці![]() ,
якщо відомі значення
,
якщо відомі значення![]() і
і![]() ,
з точністю
,
з точністю![]()
![]() ,
,
де ![]() .
.
Приклад
3.13. Наближено обчислити значення ![]() .
.
Розв’язання. В
даному випадку ![]() ,
,![]() .
Покладемо
.
Покладемо![]() ,
що відповідає
,
що відповідає![]() в
градусній мірі;
в
градусній мірі;
![]() .
.
За формулою (3.12), отримаємо:
 ,
,
тобто ![]() .
.
Для
того, щоб оцінити абсолютну і відносну
похибки, скористаємось більш точним
значенням, отриманим за допомогою
калькулятора: ![]() .
Тоді
.
Тоді![]() ,
а відносна похибка
,
а відносна похибка![]() дорівнюватиме:
дорівнюватиме:
 .
.
Приклад
3.14. Наближено обчислити значення ![]() .
.
Розв’язання. В
даному випадку  .
.
Нехай ![]() ,
,![]() ,
тоді
,
тоді![]() і
за формулою (3.12):
і
за формулою (3.12):![]() ,
отримаємо, що:
,
отримаємо, що:
 .
.
Використовуючи
калькулятор, отримаємо: ![]() .
Тоді
.
Тоді![]() ,
а відносна похибка
,
а відносна похибка![]() дорівнюватиме:
дорівнюватиме:

35 Похідні вищих порядків від функцій, заданих параметрично
. Якщо
функції ![]() і
і![]()
параметрично
задають функцію ![]() ,
то похідні
,
то похідні![]() ,
,![]() ,
можна послідовно обчислити за формулами:
,
можна послідовно обчислити за формулами:
![]() ,
,  і
т. д.
і
т. д.
Так, для похідної другого порядку має місце формула:
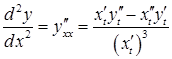 .
(3.15)
.
(3.15)
Приклад
3.19. Знайти
похідну ![]() функції
функції![]() ,
заданої параметрично:
,
заданої параметрично:![]() ,
,![]() .
.
Розв’язання.
![]()
за формулою (3.15)
![]()
